Numerical Analysis of Dry Friction－Induced Vibration of Moving Slider－Elastic Annular Beam System

，，2＊

1.Department of Mechanics，Tianjin University，Tianjin 300350，P.R.China

2.Tianjin Key Laboratory of Nonlinear Dynamics and Control，Tianjin 300350，P.R.China

0 Introduction

A friction system usually exists in the engineering such as braking system，where the friction－induced instable vibration has a negative influence on the braking system，especially the disc－pad system［1］.Many researches have been carried out for this problem with analytical，computational and experimental techniques.Various models including the single－mode approximation，the beam model，the plate model［2］and the finite element model were established to investigate the brake system of rotating brake disc acted by fixed pads.The early achievements on disc brake system are attributed to the dry frictional stick－slip self－excited vibration［3－4］and unstable structural vibration［5－6］.Stick－slip refers to a fluctuation of friction force or sliding velocity with time or sliding distance changing［7］.

In view of the stick－slip mechanism，the model of rigid body－rigid transmission belt has been widely used.In 2001，a dynamic system is presented by Galvanetto to get the mechanism of discontinuous bifurcations，where stick－slip vibration can be affected by the non－smooth bifurcations［8］.Hereby，Stribeck－type coefficient is concluded to analyze the system stability and determine the critical speed of a dynamic model with two－degree－of－freedom［9］.

However，the use of rigid belt model ignores the interaction between the brake pad and disc in transverse direction.To overcome this shortage，elastic or flexible brake disc models are adopted in recent investigations.A braking system with a flexible thick plate for disc and two continuous beams for pads by using the Mindlin′s theory is established by Beloiu and Ibrahim to account for the influence of flexible belt on the braking behaviors.The braking noise and response in time and frequency domains are investigated analytical－ly and experimentally by considering the influence of non－linearity and randomness of contact forces［10］.Nayfeh，Jilani and Manzione reduced the order of a circular flexible uniform thickness disk and analyzed its dynamical behavior analytically［11］.Recently，an elastic annular disc model is adopted for a pre－loaded mass－damp－spring system with separation and reattachment by Li，Ouyang and Guan to investigate friction－induced vibration using the improved model［12］.They found that separation often occurs in low speed，which is caused by friction during the unstable vibration.Larger in－plane stiffness and pre－load bring earlier separation and instability.In addition，the frequency of disc is increased with the effect of separation.However，the contact effect between the slider and disc and internal resonances were not considered.

During braking process，the time－dependent nature of the contacting interface in the pad－disc system is important and must be considered even if lower relative speed［5］.From the point of the rotating disc，its vibration is activated by the circumferentially moving action of the rigid pads.Influence of the moving force on brake stability attracts more and more attentions and the moving method is adopted in finite element method and experimental approaches.The deflection of a beam with moving force and the resonance velocity of the moving load are analyzed by Wayou，Tchoukuegno and Woafo［13］.An approximation solution of moving oscillator was investigated by Pesterev and Bergman to describe the variation of displacement and shear force in a one－dimensional distributed system with an arbitrarily varying speed［14］.Chen et al.analyzed a viscoelastic beam moving axially using the method of multiple scales.They found that the instability frequency intervals are influenced by the axial speed and the beam coefficient［15］.Using the finite element method，unstable frequencies of a braking system inspired by moving loads can be obtained based on the system eigenvalue analysis［16］.A linear complex－valued eigenvalue formulation for a disc with moving load is established by Cao et al.to calculate the stationary components of the disc brake［17］.Based on the finite difference method and complex eigenvalue analysis，stability and uncertain parameters analyses［18］are carried out for disc－pad systems with moving－interactions.Accordingly，Ouyang investigated the instability of a brake disc by presenting the relationship between eigenvalue and disc′s rotating speed［15］.

However，up to now，the flexible coupling between the disc and pads and the moving interactions have not been considered simultaneously in one dynamical braking model.This paper deals with a rigid－flexible coupled braking system，and focuses attention mainly on motion of the pads moving on the elastic disc.The disc is simplified as an annular beam and the friction between the beam and pads are determined using a Stribecktype friction model.Then the 1st order Galerkin reduction is applied for the beam based on result of moving load simulation.Influence of acceleration of the disc rotation on the frictional instability of the pad is investigated.

The values referred in this paper are shown in Table 1.

1 Dynamic Modals

1.1 Pads and disc

During braking，the pads move circumferentially along the outer edge of the elastic disc.So the disc can be simplified as an annular beam which is supported on uniform and continuous flexible boundary（to simulate the distribution of flexible constraint effect from the inner part of disk）［19－20］.The pad－disc coupling system is shown in Fig.1 （the boundary supporting is not included）.The pads move at relative speedVand vibrate independently in horizontal directionsX1/X2and vertical directionsY1/Y2，and the rotational angles areΦ1/Φ2［21］.For the disk，only its transverse displacementWdis considered，because it influences the pads′motion directly during braking contact.The contact stiffness involves the tangential onesKt1andKt2and the vertical oneKen.Parameters and their values of the system are listed in Table 1.

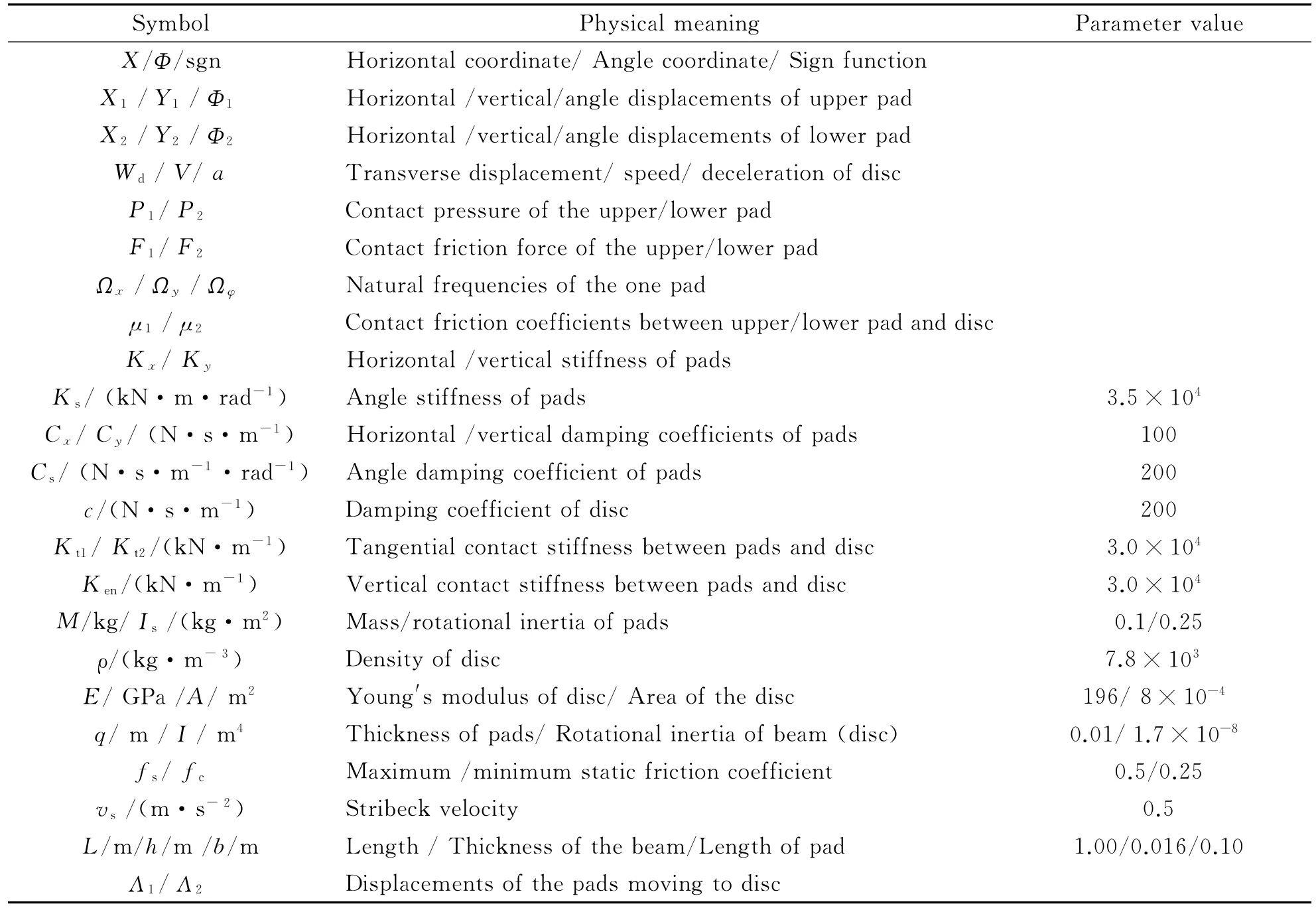
Table 1 Parameters

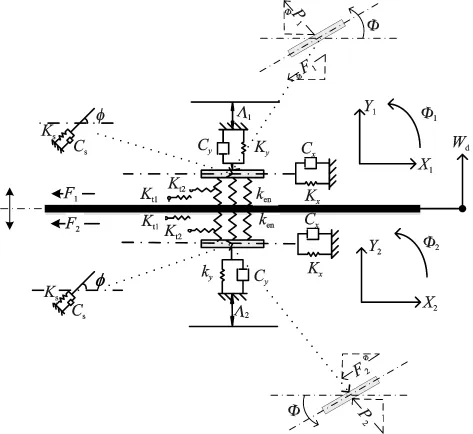
Fig.1 Pad－disc coupling system

The equations of motion of the pad－disc coupling system are deduced as andσ＝σ（T）represents the position of the loads varying with the time.

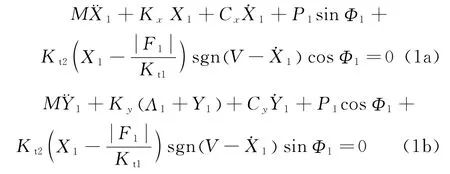
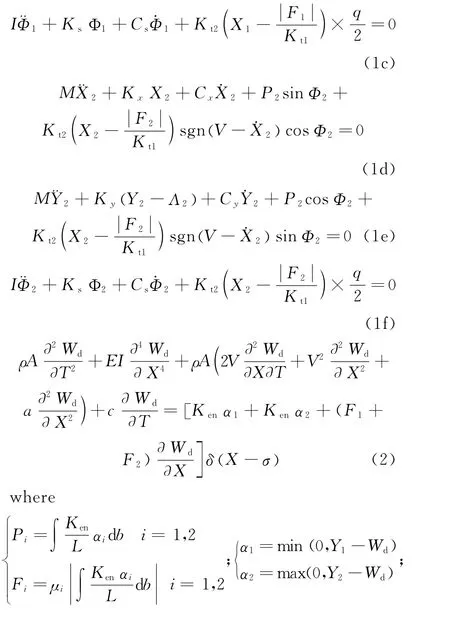
1.2 Non－dimensional Form

To rewrite the equations conveniently，introduce the dimensionless variables and parameters

1.3 Friction

Many models have been proposed to describe the friction properties，such as the coulomb friction（before occurrence of relative displacement between the contact parts），static friction（no relative velocity from static to relative motion）and－Stribeck effect，etc.

The Stribeck effect refers to a phenomenon that the friction coefficient decreases.The negative slope in relation between the friction and relative velocity is known as the main reason of friction instability.The Stribeck－type friction coefficientμ（vr）can be expressed as

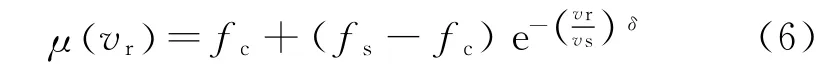
wherefcandfsare the minimum and the maximum static friction coefficients respectively，vsis the Stribeck velocity，and vrthe relative velocity.Whenδ＝1，Eq.（6）is also known as Tustin index model.The friction coefficient varies with relative velocity as shown in Fig.2.

Fig.2 Static friction and Coulomb friction with Stribeck effect

2 Moving Interaction and Galerkin Reduction

2.1 Moving load simulation

Considering a forcemoves along a straight beam.To analyze its response under the moving load，the beam is discretized intopelements.Let dtbe the unit time and dxthe unit space，the nodal forceis subsequently allocated in every unit time.

For the moving load acted system，two conditions will be dealt with during calculation：

（1）Cdx＝vdt（Cis a positive integer）.In this case，the load moves from one discrete point to theCth one after each time step dt.

（2）dx＝Cvdt（Cis a positive integer）.In this case，after each time step dt，the load moves at a place between the discrete pointseande＋1.Dividing the space step dxintoCequal subspaces，the load moves at the next sub－point after every time step dt.When the loadF槇 moves at theith one，（e＋i/Cdx）wherei＝1，2，…，C，the loadwill be resolved to the pointseande＋1as＝respectively，see Fig.3.

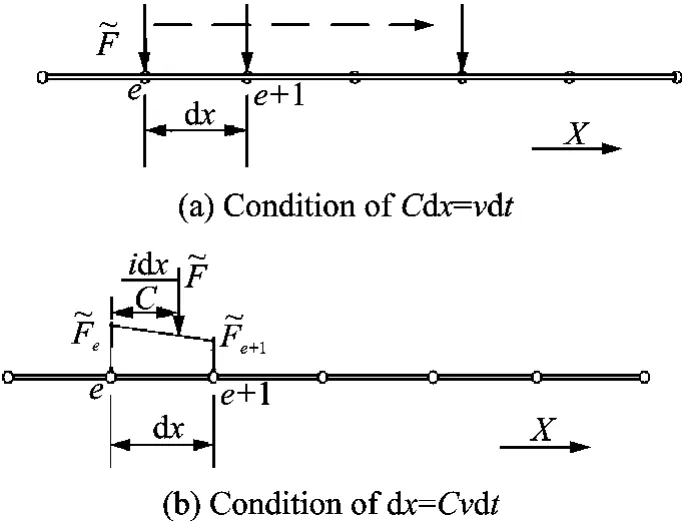
Fig.3 Moving load simulation

Corresponding to the moving load simulation mentioned above，the uniform and continuous flexible boundary of the beam should be discretized aspelastic springs with stiffnessk，as shown in Fig.4.kdepends on the material properties andp＝50in the following analysis.Then the boundary and continual conditions can be expressed as

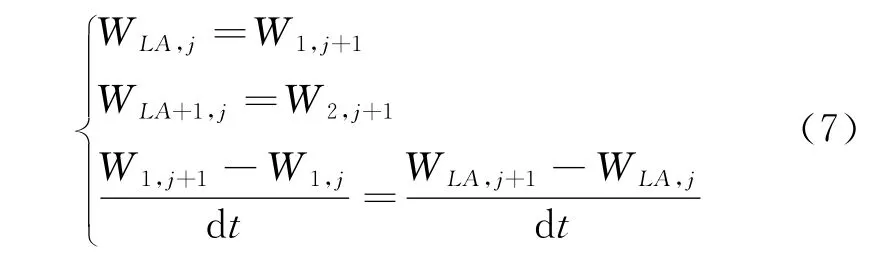
where 1，iandLAare the leftmost，theith node and rightmost node in beam′s horizontal direction，respectively.jandj＋1present thejth and（j＋1）th time moment，respectively.

Fig.4 Continuous flexible boundary discretized as p springs

The disc partial differential Eq.（5）is solved by using the finite difference method and the ordinary differential Eq.（4）is solved by Runge－Kutta method，respectively.And the dynamical behavior of the braking system with moving actions between the parts can be simulated with the same time step dt＝0.000 1and space step dx＝0.02.The transverse response of disc solved by finite difference method is transferred to contact pressure and friction force items of pads，and then Eq.（4）can be solved.Takeσ珋＝vt，then the transverse response of the beam is induced by successive change of the contact position between the pad and disc.LetKx＝5.0×104kN/m，K＝3.0×

y104kN/m，v＝2and 1，and simulation shows that both thexdirection response of the pad and the transverse response of the annular disc are periodic vibration as shown in Figs.5，6.The spectra of motions are also presented in the figures.It should be noted that except the difference of the equilibriums in velocity axis，the friction－induced dynamics of two pads are same with each other.So we present only the upper pad′s motion in this paper.

Fig.5 Response of the system under moving interactions as relative－equilibrium occuring for the pad（v ＝2）

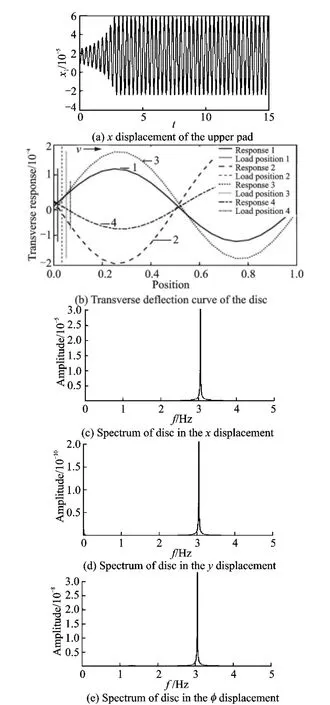
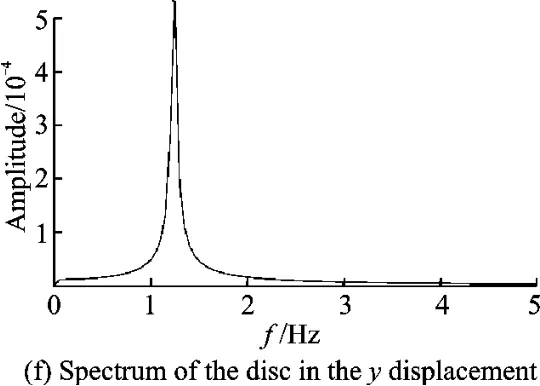
Fig.6 Response of the system under moving interactions as friction－induced limit cycle occuring for the pad（v ＝1）

Calculation shows that the natural frequencies areΩx＝3.1Hz，Ωy＝2.7Hz andΩφ＝1.3Hz for horizontal，vertical and angle direction motions of the pads，and 1.25Hz（the first order）and 2.50Hz（the second order）for transverse motion of the disk，respectively.One finds that in spectrums under higher speed sustained moving interaction，sayv＝2，motions of the pad and the disc in all directions are mixed with disc′s frequency in steady state，because the vibration frequencies are their natural frequencies and disc′s frequency in corresponding directions，respectively.However，as the moving speedvdecreases to 1，the friction－induced limit cycle vibration occurs for the pad，and common frequency 3.05Hz appears in all directions of the pad′s motion.It should be noted that even though the frictional instability has happened for the pad，the disc still vibrates in the first－order mode.So the equation of motion of the disc is discretized to the first－order mode by Galerkin model reduction in the following section.

2.2 Approximate reduction equations

Take the trial function（Eq.（8））to approximate the first－order transverse vibration of the disc.

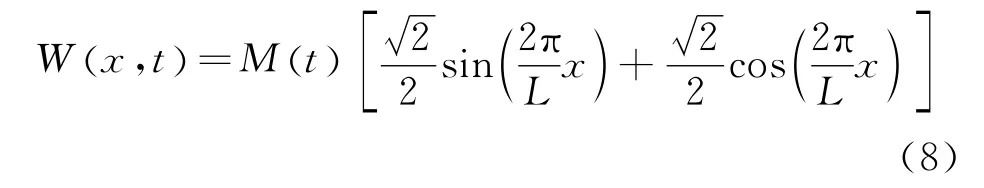
Substitute Eq.（8）into Eq.（5）and multiply the weighted function on both sides，then integrate it from 0toLinx，so the ordinary differential equation of transverse vibration of the disc is resulted as

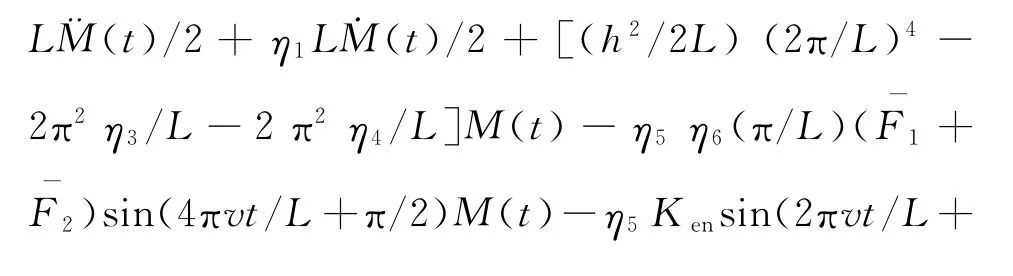
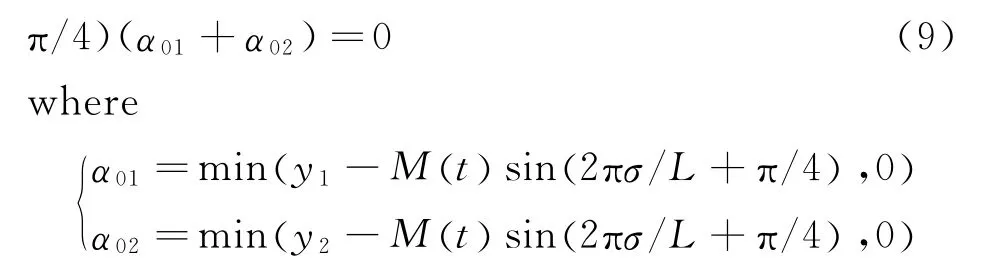
Approximation of first－order mode functionto the desired solution of transverse deflection of the disk at low speed.The time－varying function items included珋σ（t）in Eq.（9）reflect or interpret the fact that the space position of contacting load between the pads and disc varies with timet，after the vibration description for the beam is changed from a partial differential equation to an ordinary differential one.Because the stiffness value varies periodically with time，the natural frequency of the pad′s horizontal direction cannot keep in a fixed value but fluctuates periodically near 2.71Hz during integration，as shown in Fig.7.Accordingly，the system equilibrium positions will also fluctuate slightly（see the example of the angle equilibrium of pad in the vicinity of－2.678 6×10－6）.

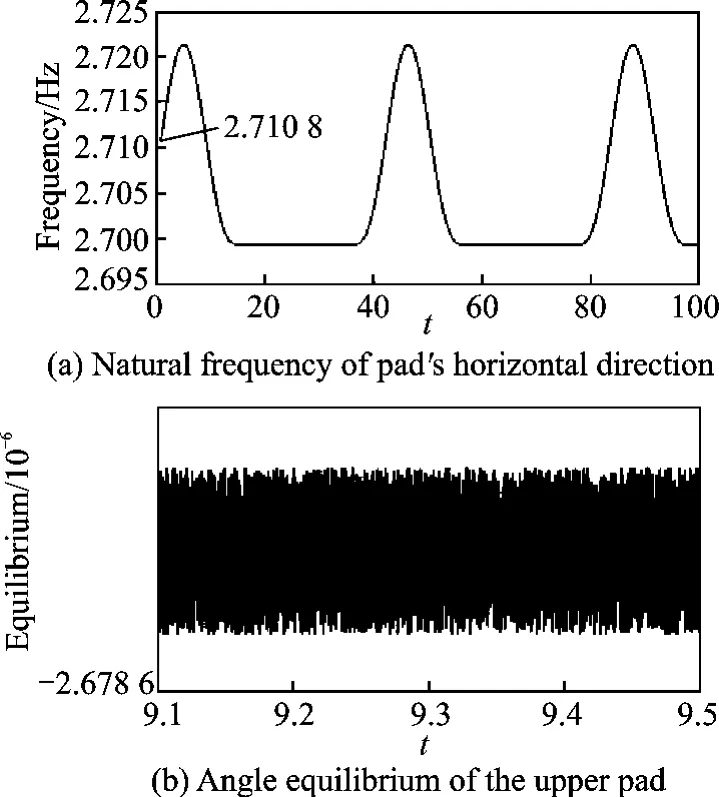
Fig.7 Fluctuations

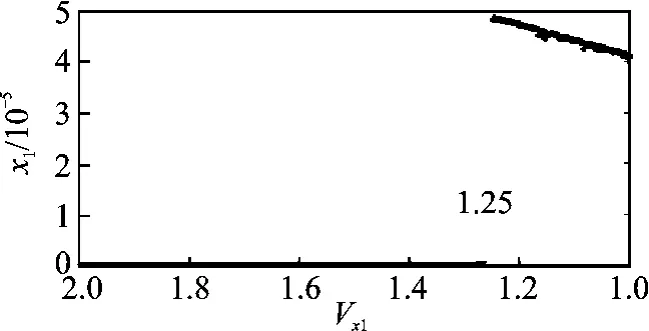
Fig.8 Bifurcation of horizontal direction of pad

Eqs.（4，5）are solved using the Runge－Kutta method，and the dynamical behavior of the braking system with moving interaction between parts can be investigated numerically.The complex eigenvalue analysis is carried out referred to Ref.［22］and the eigenvalues are 0.22＋19.58iatv＝1and－0.27＋19.58iatv＝2（assuming sign functions are positive）.The bifurcation diagram in Fig.8reveals horizontal motion of the pad under braking process with the decrease of speedv.The points are sampled when the velocity of horizontal motion is zero.The instability of motion of the pad happens and the stick－slip limit cycle is resulted atv＝1.25，which is also known as the critical speed.

3 Numerical Analyses

3.1 Non－internal resonances

To reveal the variation of the coupling system dynamics during velocity decrease process，the time histories，spectra（Fig.5（a）and Fig.6（a）），and phase portraits（Fig.9）of the selected vibration characteristics of the upper pad are presented at the speedsv＝2andv＝1，respectively.Whenv＝2，vibrations of pads will be damped，and a quasi－periodic motion occurs in this non－stationary case，which may be attributed to sustained oscillation of the contacting force resulted from the disc transverse deflection.The amplitude of upper pad inxdirection keeps vibrating with small amplitude，until changing to be an equilibrium at about 2.5×10－5.

Whenvdecreases to 1，Stribeck－type friction effect induced by self－excited vibration （or stickslip）appears and limit cycles with rather large vibration amplitude for all parts of the system are resulted（see the presented horizontal vibration of the pad in Fig.9）.

3.2 Acceleration of disc rotation

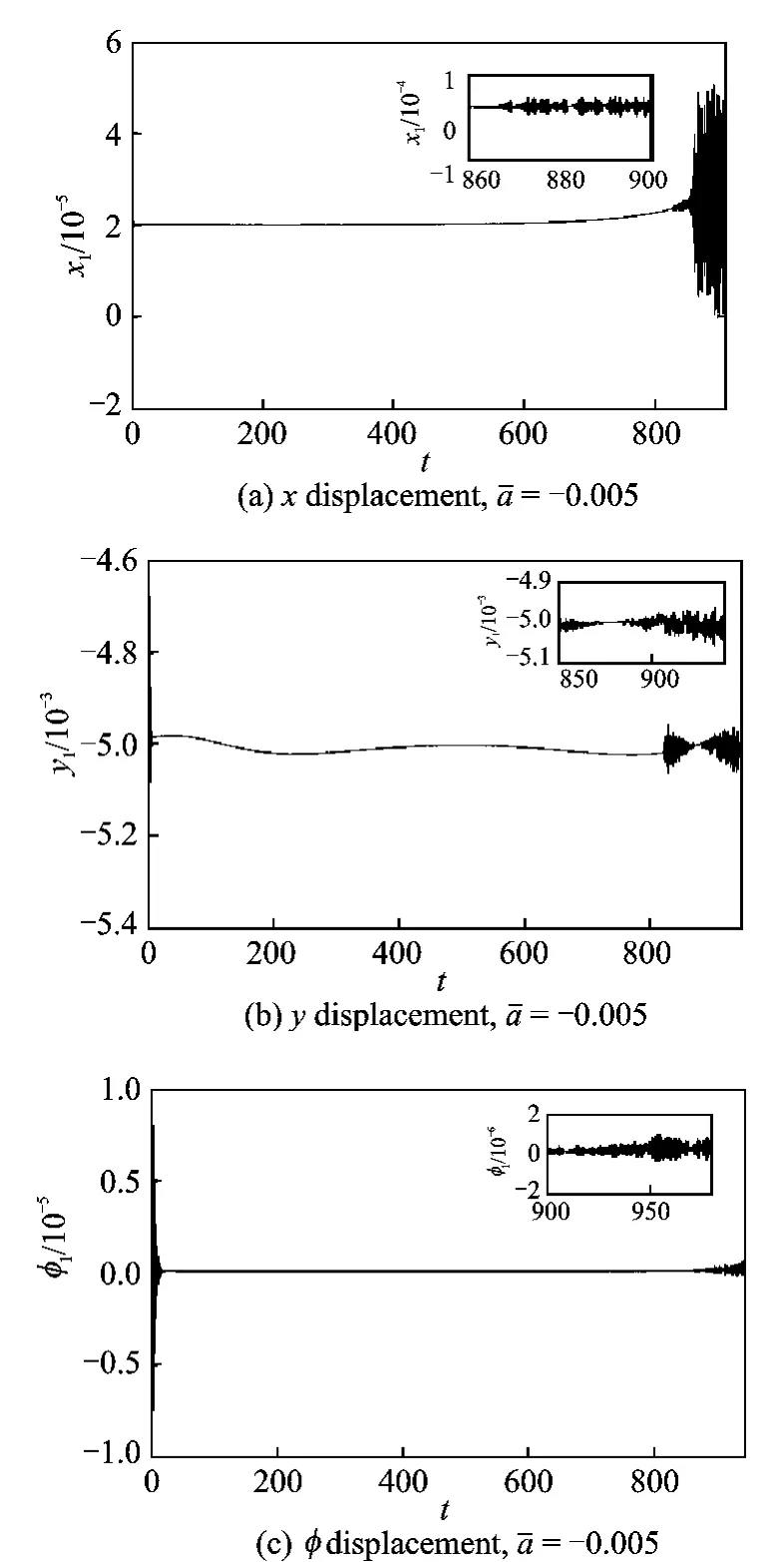
Fig.10shows the time histories of braking processes of the pads and disc at deceleration珔a＝－0.005and珔a＝－0.002，respectively.One finds that the higher the braking deceleration is，the faster the disc speed reaches to zero and the shorter the stick－slip vibration lasts.Obviously，the stick－slip vibration with high amplitude is more extensively at lower speed，where small"jitter"phenomena happens many times.As the speed approaches zero，the pads cannot stop vibration immediately.In fact，the vibration lasts for a short time under action of the relative friction force between the pads and disc.

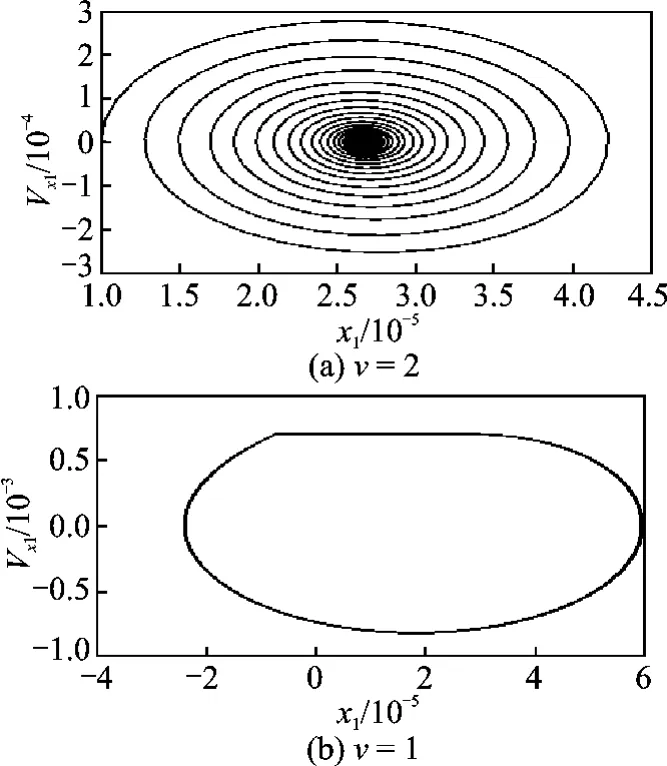
Fig.9 Phase portraits of the pad

4 Conclusions

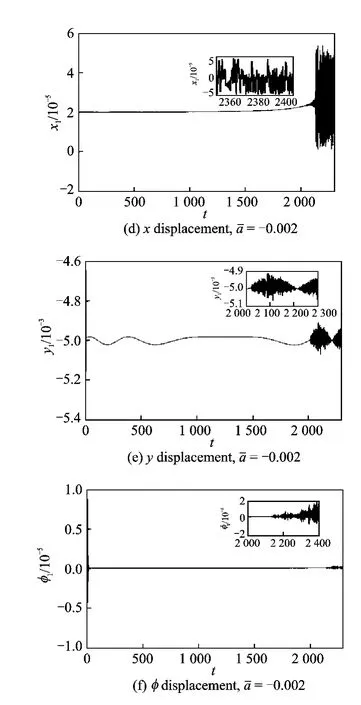
Fig.10 Dynamic responses of the upper pad

The disk－pads coupling braking system with－Stribeck－type frictional interaction with each other is investigated in this paper.The disk is simplified as an annular elastic beam and its vibration under action of moving loads is simulated using the finite difference method.Then Galerkin reduction is used for the disk vibration equation and numerical simulations are carried out for the 7－DOF equations.Conclusions are summarized in the following.

（1）Mainly the first－order mode vibration of the annular beam can be induced by frictional moving loads.By using the Galerkin reduction，the first－order mode vibration equation of the disk is resulted with time－varying stiffness，which reflects the moving contact between the pads and disk.As a result，the system equilibrium positions and natural frequency of the disc will fluctu－ate periodically during time integration.

（2）As the disc speed decreases below the critical one，the relative equilibrium of the pad in the disc loses its stability and stick－slip type vibration will be resulted in all directions′movements.As a counterpart of the pads，the disc vibrates also with large amplitude transversely.

（3）During non－stationary braking process，braking deceleration shortens the period of stickslip vibration but enlarges the vibration amplitude.In addition，small"jitter"phenomena can happen many times during process.

Acknowledgement

This work is supported by the National Natural Science Foundation of China （Nos.51575378，11272228and 11332008）.

［1］ KINKAID N M，O＇REILLY O M，PAPACLOPOULOS P.Automotive disc brake squeal［J］.Journal of Sound and Vibration，2003（267）：105－166.

［2］ OUYANG H，MOTTERSHEAD J E，BOUNDED A.Region of disc－brake vibration instability［J］.Journal of Vibration and Acoustics，2001（123）：543.

［3］ CROWTHER A R，SINGH R.Analytical investigation of stick－slip motions in coupled brake－driveline systems［J］.Nonlinear Dynamics，2007（50）：463－481.

［4］ BERNARDO M D，KOWALCZYK P，NORDMARK A.Sliding bifurcations：A novel mechanism for the sudden onset of chaos in dry friction oscillators［J］.International Journal of Bifurcation and Chaos，2003（13）：2935－2948.

［5］ OUYANG H，MOTTERSHEAD J E，LI W.A moving－load model for disc－brake stability analysis［J］.J Vib Acoust，2003（125）：53－58.

［6］ HOCHLENERT D，HAGEDORN P.Control of disc brake squeal－modelling and experiments［J］.Struct Control Hlth，2006（13）：260－276.

［7］ KANG J.Finite element modeling for stick－slip pattern of squeal modes in disc brake［J］.Journal of Mechanical Science and Technology，2014（28）：4021－4026.

［8］ GALVANETTO U.Some discontinuous bifurcations in a two－block stick－slip system［J］.Journal of Sound and Vibration，2001（248）：653－669.

［9］ WANG Q，TANG J，CHEN S，et al.Dynamic analysis of chatter in a vehicle braking system with two degrees of freedom involving dry friction［J］.Mechanical Science ＆ Technology for Aerospace Engineering，2011（30）：906－937.

［10］BELOIU D M，IBRAHIM R A.Analytical and experimental investigations of disc brake noise using the frequency－time domain［J］.Struct Control Hlth，2006（13）：277－300.

［11］NAYFEH A H，JILANI A，MANZIONE P.Transverse vibrations of a centrally clamped rotating circular disk［J］.Nonlinear Dynamics，2001（26）：163－178.

［12］LI Z，OUYANG H，GUAN Z.Friction－induced vibration of an elastic disc and a moving slider with separation and reattachment［J］.Nonlinear Dynamics，2016（87）：1045－1067.

［13］WAYOU A N Y，TCHOUKUEGNO R，WOAFO P.Non－linear dynamics of an elastic beam under moving loads［J］.Journal of Sound and Vibration，2004（273）：1101－1108.

［14］PESTEREV A V，BERGMAN L A.An improved series expansion of the solution to the moving oscillator problem［J］.J Vib Acoust，2000（122）：54－61.

［15］CHEN L Q，WU J，ZU J W.Asymptotic nonlinear behaviors in transverse vibration of an axially accelerating viscoelastic string［J］.Nonlinear Dynamics，2004（35）：347－360.

［16］SOOBBARAYEN K，SINOU J J，BESSET S.Numerical study of friction－induced instability and acoustic radiation－Effect of ramp loading on the squeal propensity for a simplified brake model［J］.Journal of Sound and Vibration，2014（333）：5475－5493.

［17］CAO Q，OUYANG H，FRISWELL M I，et al.Linear eigenvalue analysis of the disc－brake squeal problem［J］.International Journal for Numerical Methods in Engineering，2004（61）：1546－1563.

［18］L H，SHANGGUAN W B，YU D J.An imprecise probability approach for squeal instability analysis based on evidence theory［J］.Journal of Sound and Vibration，2017（387）：96－113.

［19］OBERST S，LAI J C S.Pad－mode－induced instantaneous mode instability for simple models of brake systems［J］.Mechanical Systems and Signal Processing，2015（62/63）：490－505.

［20］JOE Y G，CHA B G，SIM H J，et al.Analysis of disc brake instability due to friction－induced vibration using a distributed parameter model［J］.Int J Auto Tech－Kor，2008（9）：161－171.

［21］ZHAO Y，DING Q.Dynamic analysis of dry frictional disc brake system based on the rigid－flexible coupled model［J］.International Journal of Applied Mechanics，2015（7）：1550044.

［22］DING Q，COOPER J E，LEUNG A Y T.Hopf bifurcation analysis of a rotor/seal system［J］.Journal of Sound and Vibration，2002（252）：817－833.