Numerical simulation and qualitative analysis foran SI epidemic model via an NSFD scheme

WEI Hongyan，BAI Mei

(Department of Mathematics and Statistics,Zhoukou Normal University,Zhoukou 466001, China)

1　Introduction

In the light of the continuous-time and the discrete-timemodeling , many important and interesting results have been found in references [1-20] on the dynamical behaviors of several ecological models, species models and epidemic models. The dynamical behaviors of the continuous-time epidemic models have been widely investigated in a flood of literature. Since the statistical data on epidemics is collected in discrete time, the discrete-time models can be thought to be more convenient and accurate for describing epidemics models than the continuous-time models. Therefore, people have been received extensive attention for the research of the discrete-time epidemic models in recent time. Usually, people construct some discrete-time epidemic models by both directly making use of the property of the epidemic disease (see [1-2]) and discretizing a continuous-time epidemic model by the Euler scheme, Runge-Kutta method, Mickens’ non-standard discretization method and some other standard finite schemes. Based on these methods, the computation of the basic reproduction number, the local stability and global stability of the disease-free equilibrium and the endemic equilibrium, the extinction, permanence and persistence of the disease have been investigated in [3-13]. In particular, there are several studies on epidemic models with varying total population size, for example, Sun and Hsieh in [23] studied global analysis of an SEIR model with varying population size. Kuniya et al in [21] studied global stability of a multi-group SIS epidemic model with varying total population size. In [22], Nakata et al studied global dynamics of a class of SEIRS epidemic models in periodic environment. Moreover, Muroya et al in [24] studied global stability for a discrete epidemic model for disease with immunity and latency spreading in a heterogeneous host population.

Recently, under the assumption that the population is constant, Cui et al have studied the local stability and the global stability of a discrete SIR epidemic model with vaccination by NSFD scheme (see [19-20]).

Now, we consider the following SI epidemic model with varying total population size

(1)

where the populationN(t)=S(t)+I(t) can vary, the birth process incorporates density dependent effects through a logistic equation with intrinsic growth raterand the carrying capacityK, and other parameters are positive constant.

It is obvious that system (1) is a two-dimensional nonlinear ODE, instead of obtaining its analytical solutions to study the global stability, we focus on solving numerical solutions or approximate solutions of system (1) according to different discrete difference schemes and giving the explicit expression of the basic reproduction numberR0by developing the methods given in [14-18]. Therefore, motivated the above, in the paper, we implement a non-standard finite difference (NSFD) scheme to (1) by Mickens in [14-18] to obtain the following discrete-time SI epidemic model

(2)

where the denominator function [14-15] is given by

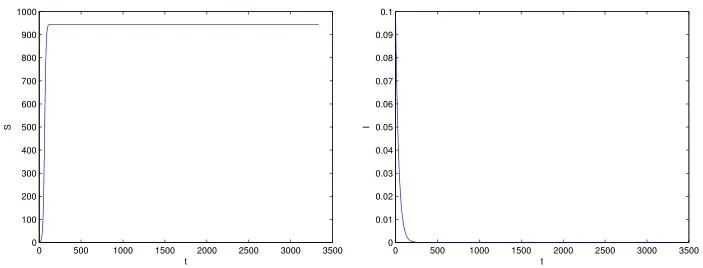
(a)　　　　　　　　　　　　 (b)Figure 1　Number solution at the initial value point (0.9,0.1) with β=0.01;

(3)

We rearrange (2) to get a explicit version of (2) as follow

(4)

Since all parameters in discrete model (2) are positive, it is clear that if the initial valuesS0>0,I0>0, then the numerical solutions will also be positive for alln>0, namelyS0>0,I0>0,⟹Sn>0,In>0.

This paper is organized as follows. In the next section, we present the important properties of the solutions for model (2). We obtain a sufficient condition for the global asymptotic stability of the equilibria in Section 3. In Section 4, we give the numerical simulations to demonstrate the validity of our theoretical analysis.

2　Basic properties

By adding the two equations of (2) together, we can obtain the exact scheme for the conservation law about Eq(2)

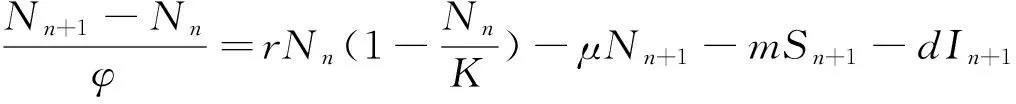
(5)

whereNn=Sn+In. From Eq(5), it is easy to see that the total populationNnsatisfies the following inequality:

Nn+1…

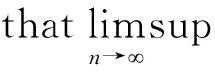
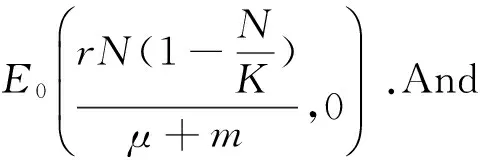
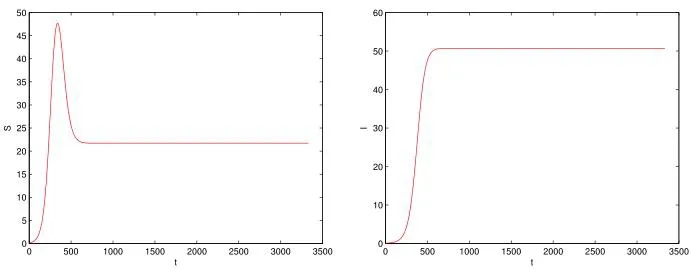
(a)　　　　　　　　　　　　 (b)Figure 2　Number solution at the initial value point (0.9, 0.1) with β=0.1;

3　Global Stability of equilibria

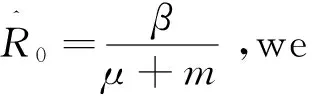
Theorem3.1

(6)

Proof. The disease-free equilibriumE0(S0,I0) satisfies the following equations:

(7)

(a)　　　　　　　　　　　　 (b)Figure 3　Bifurcation diagrams of system (2) with β=0.5;d=0.5;

SettingXn=Sn-S0and using (5), we can rewrite (2) as follows

(8a)

(8b)

Define

(1+φ(μ+d))S0In.

(9)

(10)

By Eq(10) we get that

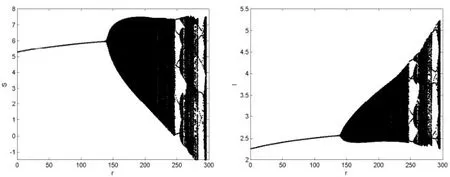
(a)　　　　　　　　　　　　 (b)Figure 4　Bifurcation diagrams of system (2) with β=1;

Obviously, we get

(i)R01⟺ΔVn0,

(ii)R0<1,ΔVn=0⟺Xn+1=0,In=0,

(11)

(iii)R0=1,ΔVn=0⟺Xn+1=0.

By (7) and (11), we have

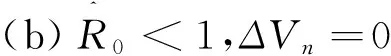
(12)

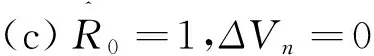
Now , we show thatΔVn=Vn+1-Vn<0.

ΔVn=Vn+1-Vn

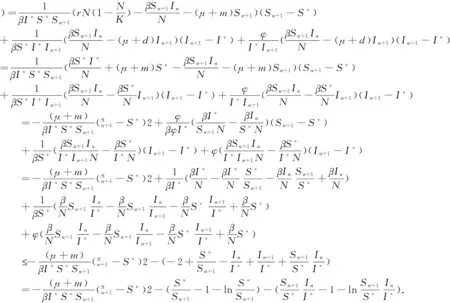
According to the above equation, we knowΔVn=0⟺Sn+1=S*,In+1=In.Substituting them into model (2), we get that the only compact invariant set with {ΔVn=0}is the singleton{E*}, By LaSalles Invariance Principle,we have {E*}is globally asymptotically stable in Ω for allh.

4　Numerical simulation

In this section, we perform some numerical results for model (2). All computations are carried out by MATLAB.

Case 1. Let us choose the following initial conditions S(0) = 0.1 and I(0) = 0.9. In order to investigate the theoretical results involved in Theorem 3.2. We chooseβ=0.01；r=0.4;d=0.1;μ=0.002;m=0.02;k=1 000;ψ=0.3;R0=0.098<1, the disease-free equilibriumE0is global asymptotically stable. Fig. 1(a) shows that the susceptible population converges to a positive steady state, the infected population converges to zero.

Case 2. Let us choose the following initial conditions S(0) = 0.1 and I(0) = 0.1. In order to investigate the theoretical results involved in Theorem 3.3. We chooseβ=0.1；r=0.1;d=0.01;μ=0.02;m=0.002;k=100;ψ=0.3;R0=3.333 3>1, the epidemic equilibriumE*is global asymptotically stable. Fig. 2 shows that the susceptible population and infected population converge to the positive steady state, respectively.

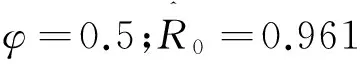
5　Discussion

In this paper, we present an analysis of model (2), and we develop a new nonstandard finite difference scheme to provide several simulations. Some important features of the scheme such as the positivity property, equilibrium point and the boundedness of the solution for continuous model are maintained through this discretization method. Moreover, by using the method mentioned in [19-20], we also obtain that the local stable of the disease-free equilibrium and endemic equilibrium of discrete model (2) and by constructing suitable Lyapunov functions, we obtain sufficient conditions for the global behaviors of the disease-free equilibrium and the endemic equilibrium. Our results demonstrate that the dynamic behavior of the discretized system is in keeping up with the continuous model and amplifies the conclusions in the literature. For our future work, we should consider the Hopf bifurcation, turning instability of the discretized model with time delay and diffusion.

6　Disclosure statement

No potential conflict of interest was reported by the authors.

[1]J E Franke, A A Yakubu. Disease-induced mortality in density-dependent discrete-time S-I-S epidemic models[J]. J.Math.Biol, 2000, 57:755-790.

[2]C Castillo Chavez, A A Yakubu. Discrete-time SIS models with complex dynamics[J]. Nonlinear Anal, 2001, 47:4753-4762.

[3]R Willoxa, B Grammaticosa, A S Carsteab, et al. Epidemic dynamics: discrete-time and cellular automaton models[J].Physica A, 2003, 328:13-22.

[4]L J S Allen, P Driessche. The basic reproduction number in some discrete-time epidemic models[J]. J. Difference Equ. Appl,2008, 14：1127-1147.

[5]X Li, W Wang. A discrete epidemic model with stage structure[J]. Chaos Solitons Fractals, 2005,26：947-958.

[6]L Li, G Sun, Z Jin. Bifurcation and chaos in an epidemic model with nonlinear incidence rates[J]. Appl. Math. Comput, 2010, 216:1226-1234.

[7]L J S Allen. Some discrete-time SI, SIR, and SIS epidemicmodels[J]. Math. Biosci, 1994, 124:83-105.

[8]L J S Allen, Y Lou, A L Nevai. Spatial patterns in a discrete-time SIS patch model[J]. J. Math. Biol, 2009，58: 339-375.

[9]J E Franke, A A Yakubu. Discrete-time SIS epidemic model in a seasonal environment[J]. SIAM J. Appl. Math, 2006, 66:1563-1587.

[10]V Mendez, J Fort. Dynamical evolution of discrete epidemicmodels[J]. Physica A, 2000, 284:309-317.

[11]M Sekiguchi. Permanence of a discrete SIRS epidemic model with time delays[J]. Appl. Math. Lett, 2010, 23: 1280-1285.

[12]Y Muroya, A Bellen, Y Enatsu, et al. Global stability for a discrete epidemic model for disease with immunity and latency spreading in a heterogeneous host population[J]. Nonlinear Anal. RWA, 2012,13: 258-274.

[13]Y Muroya, Y Nakata, G Izzo, et al. Permanence and global stability of a class of discrete epidemic mod-els[J]. Nonlinear Anal. RWA, 2011,12:2105-2117.

[14]R E Mickens. Application of Nonstandard Finite Difference Schemes[M]. Singapore:World Scientific, 2000.

[15]R E Mickens. Calculation of denominator functions for nonstandard finite difference schemes for differential equations satisfying a positivity conditon[J]. Numer Methods Partial Differ. Equ, 2007,23:672-691.

[16]R E Mickens. Nonstandard Finite Difference Model of Differential Equations[M]. Singapore:World Scientific, 1994.

[17]R E Mickens. Application of Nonstandard Finite Difference Schemes[M]. Singapore:World Scientific, 2000.

[18]R E Mickens. Advances in the Applications of Nonstandard Finite Difference Schemes[M]. Singapore:World Scientific, 2005.

[19]Q Cui, X Yang, Q Zhang. An NSFD scheme for a class of SIR epidemic model with vaccination and treatment[J]. J.Differ. Equ. Appl., 2014, 3:416-422.

[20]Q Cui,Q Zhang. Global stability of a discrete SIR epidemic model with vaccination and treatment[J]. Journal of Difference Equations and Applications, 2015,21(2):111-117.

[21]T Kuniya, Y Muroya.Global stability of a multi-group SIS epidemic model with varying total population size[J]. Applied Mathematics and Compuation, 2015,265:785-798.

[22]Y Nokata,T Kuniya. Global dynamics of a class of SEIRS epidemic models in periodic environment[J]. Journal of Mathematical analysis and Applications, 2010,363:230-237.

[23]C Sun, Y H Hsieh. Global analysis of an SEIR model with varying population size[J]. Applied Mathematical Modelling, 2010,34:2685-2697.

[24]Y Muroya, Y Enatsu, Y Nakata. Global stability for a discrete epidemic model for disease with immunity and latency spreading in a heterogeneous host population[J]. Nonlin.Anal.RWA, 2012,13:258-274.