扁管凝结换热的试验研究

童正明 祝佳栋 周清童

摘 要： 对某散热器有限公司提供的两种型号的冷却扁管进行了管外凝结换熱试验。采用线性回归法（最小二乘法）拟合出换热系数与管内流体流速之间的关系，并利用测量值的方差σ2对拟合方程的精度进行检验。从拟合方程得到两种试验扁管管内外换热准则关系式，管型Ⅰ和管型Ⅱ的管外凝结换热系数分别为11 981.78、11 004.74 W·m-2·K-1。从拟合方程和两种管型的长宽比可以得出：扁管的长宽比越大，管内流体的湍流越充分，越有利于管内对流换热，但不利于管外凝结换热。

关键词： 车用散热器； 扁管； 对流换热系数； 凝结换热

中图分类号： TK 124 文献标志码： A

Experimental Study on Condensation Heat Transfer

of the Flat Tube

TONG Zhengming， ZHU Jiadong， ZHOU Qingtong

（School of Energy and Power Engineering， University of Shanghai for Science

and Technology， Shanghai 200093， China）

Abstract： Experimental studies on the condensation heat transfer on the outside of two types of the cooling flat tubes，provided by a radiator company，were conducted.In the test，the relationship between the heat transfer coefficient and the flow rate in the tube was fitted by the linear regression.The accuracy of the fitted equation was verified by the variance σ2 of the measured values.The coefficients of 11 981.78 W·m-2·K-1 for type Ⅰ and 11 004.74 W·m-2·K-1 for type Ⅱ were achieved.According to the fitted equation and the ratio of length and width for two types of the flat tubes，it could be concluded that the larger the ratio was，the fuller the turbulent flow in the tube developed.It was helpful to the convective heat transfer.But it was adverse to the condensation heat transfer in the outside of the tube.

Keywords： automobile radiator； flat tube； convective heat transfer coefficient； condensation heat transfer

汽车工业的快速发展给汽车散热器带来巨大的市场。为了提高散热器的换热性能以满足车用散热器日益增长的技术要求，就需要对换热元件的换热机理做深入的研究[7]。对散热器中起主要换热作用的冷却扁管进行研究非常重要。本文对某散热器有限公司提供的两种型号的冷却扁管进行了管外凝结换热试验，主要包括试验和数据处理两方面的工作。

1 凝结换热

一般蒸汽与低于饱和温度的壁面接触时有两种不同的凝结形式。如果凝结液体能很好地润湿壁面，它就在壁面铺展成膜，这种凝结形式称为膜状凝结。膜状凝结时，壁面总是被一层液膜覆盖，凝结放出的相变热（潜热）必须穿过液膜才能传到冷却壁面上。这时液膜层是换热的主要热阻。当凝结液体不能很好地润湿壁面时，凝结液体在壁面上形成一个个的小液滴，这种换热形式称为珠状凝结。对于珠状凝结，虽然其表面传热系数要比其他条件相同的膜状凝结大几倍或更多，但却不易于长久地维持。因而实际工业上应用只能实现膜状凝结[1]。

能源研究与信息2018年 第34卷

第1期童正明，等：扁管凝结换热的试验研究

努塞尔于1916年提出了纯净蒸汽层流凝结的分析解，指出了液体膜层的导热热阻是凝结过程主要热阻，忽略次要因素，从理论上揭示了有关物理参数对凝结换热的影响。

努塞尔的理论分析可以推广到水平圆管及球表面上的层流膜状凝结。平均表面传热系数的计算式[2-3]为

hH=0.729grρ2lλ3lμld（ts-tw）1/4（1）

hs=0.826grρ2lλ3lμld（ts-tw）1/4（2）

式中：hH为水平圆管上的层流膜状凝结换热系数，W·m-2·K-1；hs为球表面上的层流膜状凝结换热系数，W·m-2·K-1；r为液体的汽化潜热，kJ·kg-1；ρl为液体的密度，kg·m-3；λl为液体的导热系数，W·m-1·K-1；μl为液体的动力黏度，Pa·s；d为水平管或球的直径，m；tw为壁面温度，℃；ts为液体温度，℃。

膜层中凝结液有层流和湍流之分，可以用膜层雷诺数Re进行判别。试验表明，液膜由层流转变为湍流的临界雷诺数Rec可定为1 600。横管因直径较小，实践上均处在层流范围。因而将在本文求解得到的管外凝结换热系数与式（1）进行比较。

2 蒸汽凝结试验台

为了获取试验数据，笔者自行设计了一台蒸汽凝结换热的试验装置。该装置主要由蒸汽系统、冷却水循环系统、测量系统等组成。

2.1 试验原理

由蒸汽发生器产生的蒸汽进入装有试验元件扁管的试验工作位内进行热交换。冷却水流经试验管，带走蒸汽凝结所放出的热量。为了防止蒸汽发生器产生的蒸汽中携带水分，从而影响试验的精度，必须控制蒸汽的干度，将蒸汽压力控制在0.12 MPa左右，温度控制在104～105℃。

蒸汽在扁管表面上凝结，凝结水经测试端体下方的阀门流出后由电子天枰称重。冷却水流量则经过涡轮流量计计量，冷却水流经试验管后，吸收热量而使水温升高，两端的温度通过温差热电堆测量。通过冷却装置控制冷却水进口温度使其在试验过程中保持稳定。由于进口温度相同，一方面使冷却水系统稳定，另一方面便于对试验结果进行分析对比。在维持蒸汽温度和流速恒定的条件下，测量管内冷却水流速和换热系数之间的关系。

扁管传热系数K可以根据传热基本方程式求得。由热阻叠加原理得到如下关系[1]，即

1K=1αo+R+1αi（3）

式中：R为管壁热阻、污垢热阻、接触热阻等所有导热热阻，m2·K·W-1；αo为管外凝结换热系数，W·m-2·K-1；αi为管内冷却水换热系数，W·m-2·K-1。

在试验期间R可以被认为是不变的常数。试验中由于蒸汽压力不变，且其定性温度基本不变，则αo在整个试验期内为常数。由于试验扁管的厚度δ为0.2 mm，且扁管铝材的导热系数比较大，故管壁热阻可以忽略不计；另外，由于试验扁管测试前清洗干净，故污垢热阻可忽略不计。故求出热阻R′就可以得出管外蒸汽凝结换热系数。于是有

1K=1αi+R′（4）

式中，R′为忽略管壁热阻、污垢热阻后的导热热阻，m2·K·W-1。

如果认为水在所试验的温度范围内，所有物性都与温度的变化无关，则式（4）可简化为

1K=R′+Cu-n（5）

式中：C、n均为常数；u为管内侧的冷却水流速，m·s-1。

通过试验测得u和K后，就可以作出1/K与u的拟合曲线，从而得出R′、C、n。

2.2 試验装置及系统

2.2.1 试验系统

试验台如图1所示。试验时，调整冷却水流速分别为3.0、2.0、1.4、1.2、1.0、0.8 、0.6、0.4 m·s-1，测量冷却水进口温度tw1、冷却水进出口电势差ΔV、冷却水体积流量Gw、冷凝水质量流量m和饱和蒸汽温度。

图1 试验台

Fig.1 Test sytem

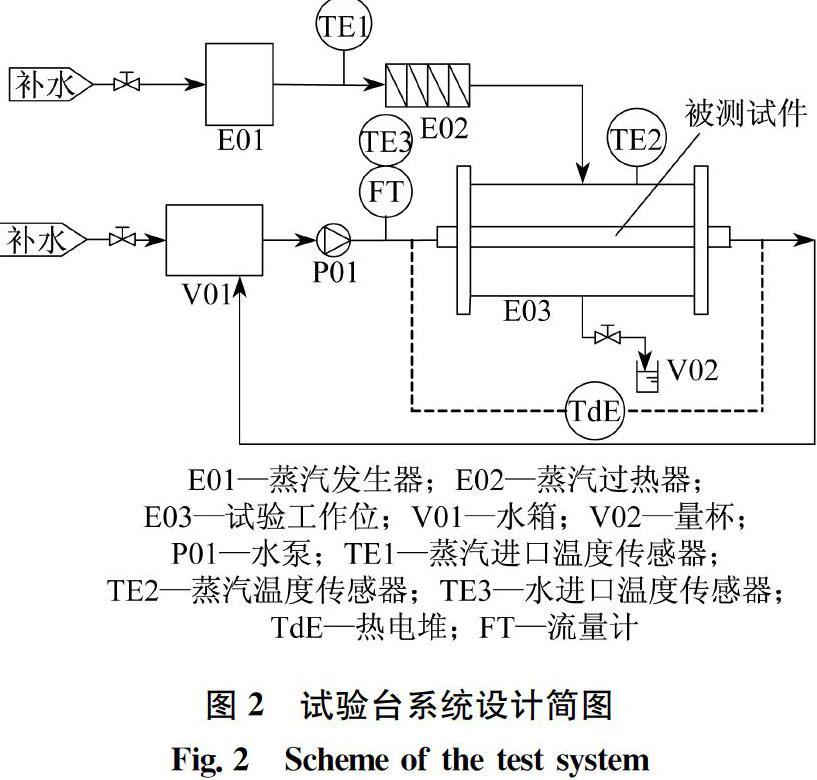
试验台系统设计简图如图2所示。换热扁管安装在横截面尺寸为150 mm×180 mm、长为1 000 mm的长方体试验工作位内。

2.2.2 试验测试扁管

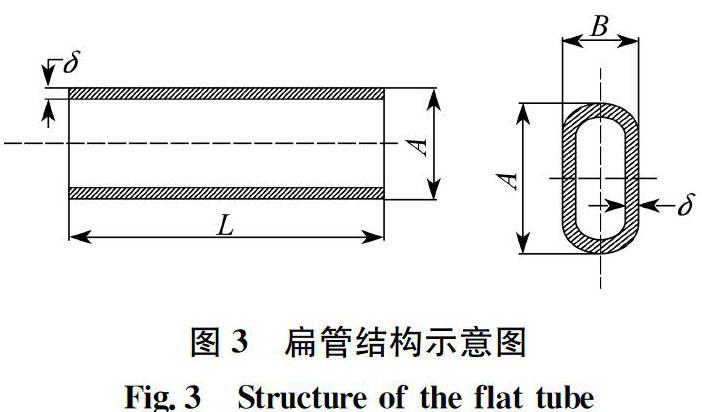
对两种管型的铝材扁管进行试验研究，管型分别为：管型Ⅰ（2.5 mm×14 mm×1 010 mm）和管型Ⅱ（2.2 mm×19 mm×1 010 mm），管壁厚度均为0.2 mm。扁管结构示意图如图3所示，其中：A、B分别为扁管长、短边长度；L为扁管的长度。

图2 试验台系统设计简图

Fig.2 Scheme of the test system

图3 扁管结构示意图

Fig.3 Structure of the flat tube

3 试验数据处理及分析

3.1 试验参数

3.1.1 试验直接测量参数的记录

扁管管内工质为自来水，管外为饱和蒸汽。两种扁管的一组试数据分别如表1、2所示。

表1 管型Ⅰ的一组试验数据

Tab.1 Test data of the type I tube

表2 管型Ⅱ的一组试验数据

Tab.2 Test data of the type II tube

从表1、2中可知，随着冷却水流速的减小，冷却水流量、冷凝水质量也相应减小，此时冷却水的进口温度、电势差均有所增加。

3.1.2 试验参数的计算

（1） 当量直径de [4-5]和管内雷诺数Re

流体在管内流动比较复杂，而扁管由于自身的几何形状，其流动形态不同于圆管，为此根据文献[6]求取扁管的当量直径为

de=4[B（A-B）+πB2/4]πB+2（A-B）（6）

雷诺数Re为

Re=deuρμ（7）

式中：μ为流体黏度，kg·m-1·s-1；ρ为流体密度，kg·m-3。

（2） 冷却水出口温度tw2

tw2=2.763+8.624（ΔV+Et）-

0.088（ΔV+Et）2（8）

式中：Et为对应温度的电势差，mV；tw2为冷却水出口温度，℃。

（3） 总换热量Q

Q取冷却水侧换热量Qc与蒸汽侧换热量Qh的算术平均值，即

Q=Qc+Qh2（9）

（4） 传热系数K

K可根据传热基本方程式得到，即

K=QFΔtm（10）

式中：Δtm为对数平均温差，℃；F为扁管换热面积，m2。

通过计算得到的两种型号扁管的尺寸如表3所示。

表3 两种型号扁管的尺寸

Tab.3 Geometric parameters of two flat tubes

由式（5）可知，当u逐渐增大时，1/K将无限趋近于R′，故可根据试验数据中1/K与u的关系作图，结果如图4所示。将从图中得出的R′的初始近似值作为R′0，取R′0=0.000 6，再利用线性回归法计算a和b。

根据最小二乘法得到残余误差方程（σi为yi的残余误差）的数学模型为

yi=a+bxi+σi， i=1、2、…、n（13）

根据最小二乘法，a和b应在（试验数据每组取八个速度点故n值取8）θ=∑8i=1σ2i最小时为最佳值，故对式（13）中a和b取偏导数并令其为零，即

图4 1/K与u关系散点图

Fig.4 Relationship between 1/K and u

θa=2∑8i=1（a+bxi-yi）=0（14）

同理，有

θb=2∑8i=1（axi+bx2i-xiyi）=0（15）

联立式（14）、（15）得到

b=LxyLxx

a=y—-bx—

Lxx=∑8i=1x2i-18∑8i=1xi2

Lxy=∑8i=1xiyi-18∑8i=1xi∑8i=1yi

x—=18∑8i=1xi

y—=18∑8i=1yi（16）

经计算，b=-1.857 2，a=-8.054 0，C=0.000 317 8，n=1.857 2。

则有

y=-8.054 0-1.857 2x（17）

1K=0.000 6+0.000 317 8u-1.857 2（18）

将式（18）作图，结果如图5所示，并与图4的散点关系图做比较。

从图5中可看出，管型I的擬合曲线基本与试验数据相符，仅在较低流速时存在较大偏差。

3.2.2 回归方程方差检验

对方程精度的检验用测量值yi的方差σ2检验。因a和b已知，所以由式（13）可得残余误差。

图5 1/K与u拟合曲线

Fig.5 Fitting curve of 1/K and u

方差σ2的估计误差σ21（因本方程只有两个未知量，故自由度为n-2）为

σ21=∑8i=1σ2i6=0.328 9（19）

由于σ2的方差较大，故需调整R′0的初始值，取R′1=R′0-0.000 001，再代回到式（11）中循环计算，直到方差满足σ2<0.000 1。最后求得的拟合方程为

1K=0.000 083 46+0.000 953 2u0.62（20）

由式（20）和式（7）可得到管型Ⅰ的管内对流换热的准则关系式，即

Nu1=0.037 56Re0.62（21）

式中，Nu1为努塞尔数。

管型Ⅰ管外凝结换热系数为11 981.78 W·m-2·K-1。

由管内对流换热系数并根据牛顿冷却定律，求出管壁温度，再代入膜层雷诺数计算式得到膜层雷诺数为2.027。

因为膜层雷诺数小于1 600，属于层状凝结换热。将计算得到的管型Ⅰ管外凝结换热系数与式（1）进行比较，得到管型Ⅰ管外换热系数的计算式为

h1=0.425grρ2lλ3lμlde（ts-tw）1/4（22）

则管外凝结换热的准则关系式为（偏差在±25%以内）

Nu1=h1deλ=0.002 321grρ2lλ3lμlde（ts-tw）1/4（23）

同理，求得管型Ⅱ的拟合方程为

1K=0.000 090 87+0.000 908 7u0.65（24）

管内对流换热的准则关系式

Nu2=0.034 12Re0.65（25）

式中，Nu2为管内对流换热的努塞尔数。

管外凝结换热系数为11 004.74 W·m-2·K-1，膜层雷诺数为6.284。管外换热系数计算式为

h2=0.523grρ2lλ3lμlde（ts-tw）1/4（26）

管外凝结换热的准则关系式为

Nu2=h1deλ=0.002 568grρ2lλ3lμlde（ts-tw）1/4（27）

4 结 论

在管外凝结换热工况下，保持管外蒸汽温度及流速一定，测量传热系数与管内冷却水流速的关系。采用线性回归法（最小二乘法）拟合换热系数与管内流速的关系进行拟合，并对拟合方程的精度利用测量值的方差σ2进行检验，从而直接得到管内对流换热的准则方程式以及管外凝结换热系数。

从两种管型的管内外换热系数准则关系式以及长宽比（A/B）可以得出，扁管长宽比越大，管内流体湍流越充分，有利于管内对流换热，而不利于管外凝结换热。

参考文献：

[1] 杨世铭.传热学[M].3版.北京：高等教育出版社，2005：207-211.

[2] DHIR V K，LIENHARD J H.Laminar film condensation on plane and axisymmetric bodies in nonuniform gravity[J].Journal of Heat Transfer，1971，93：97-100.

[3] POPIEL C O，BOGUSLAWSKI L.Heat transfer by laminar film condensation on sphere surfaces[J].International Journal of Heat & Mass Transfer，1997，18（12）：1486-1488.

[4] 王静波.新型当量直径——动量当量直径[J].矿山机械，2007，35（12）：41，42.

[5] 童正明，王亦凡，陈丹.汽车散热器结构优化研究[J].能源研究与信息，2014，30（2）：108-112.

[6] 朱聘冠.换热器原理及计算[M].北京：清华大学出版社，1987：132-133.

[7] 徐之平，王锦侠.桑塔纳轿车的不同结构国产散热水箱热性能分析研究[J].能源研究与信息，1996，12（1）：13-23.

（上接第55页）

[6] 朱幼君，欧阳华，杜朝辉.低噪声风洞的气动和结构设计[J].发电设备，2012，26（4）：222-225.

[7] 白江涛，朱惠人，张宗卫，等.叶片全表面换热系数和冷却效率的实验测量[J].西安交通大学学报，2010，44（11）：92-97.

[8] 郭涛，朱惠人，许都纯，等.热色液晶瞬态测量全表面换热系数的技术研究[J].测控技术，2006，25（9）：67-69，74.

[9] 白江涛，朱惠人，刘存良.双参数传热实验的液晶瞬态测量不确定度分析[J].航空动力学报，2009，24（9）：1945-1951.

[10] 黄竞，何雅玲，陶文铨.型线参数对低速风洞收缩段的影响[C]∥中国工程热物理学会第十一届年会论文集流体机械.北京：中国工程热物理学会，2005.

[11] 伍荣林，王振羽.风洞设计原理[M].北京：北京航空学院出版社，1985：40.

[12] 刘政崇.高低速风洞气动与结构设计[M].北京：国防工业出版社，2003.第34卷 第1期能源研究与信息Energy Research and InformationVol.34 No.1 2018