二次函数在闭区间上的值域问题探究
(云南省丽江市华坪县第一中学 云南华坪 674800)
一、提出问题
非典型二次函数求值域是高中数学的高频考点,因其在试卷中通常以非典型的形式出现,使它成为了近年高考的热点。由于其非典型形式众多,且可以与很多高中数学知识点例如向量、三角函数等结合起来,很具有迷惑性。事实上只要理解并总结它的几种非典型形式,透过现象认识本质,可以把它转化为我们熟悉的知识进行计算求解。
二、准备知识
1.一般二次函数当α>0时图像为开口向上的抛物线,对称轴自变量x距离对称轴远函数值大,反之小,值域为y≥(4α c -b²)/4αc;当 α<0时图像为开口向下的抛物线,对称轴自变量x距离对称轴远函数值小,反之大,值域为
三、典型二次函数求值域
1.定轴,定区间型
例1、已知二次函数f(x)=-x²+4x+9,求f(x)在-2≤x≤3的值域。
解:此二次函数的图像开口向下,对称轴x=2。由于2和-2距离对称轴x=2分别最近、最远,故在2和-2处分别取得最大值、最小值,值域为-3≤y≤13。
2.动轴,定区间型
例2、已知二次函数f(x)=x²-2αx+b,求f(x)在闭区间[-1,1]上的值域。
解:分析:此二次函数的图像开口向上、对称轴x=α。确定不了区间[-1,1]上的点到对称轴x=α的距离哪个远哪个近,故要讨论区间[-1,1]相对对称轴x=α的位置以定远近。
当α<-1时,区间[-1,1]在对对称轴x=α 的右边,值域为[1+2α+b,1-2α+b]
当α>1时,区间[-1,1]在对对称轴x=α 的左边,值域为[1-2α+b,1+2α+b]
当-1≤α≤1时,对称轴x=α 在区间[-1,1]上,显然α距离对称轴近,但确定不了哪个端点距离对称轴远,故需以区间[-1,1]的中点为界再分两种情况讨论:即当-1≤α≤0时值域为[-α²+b,1-2α+b];当0<α≤1 时值域为[-α²+b,1+2α+b]。
3.定轴,动区间型
解法与2类似:主要讨论区间与对称轴的位置以定远近,此处不再详表。
分析:此类型题难度一般,无外乎弄清二次函数图像的开口方向、定义域上的点与对称轴距离的远近。唯一的难点是动区间或动对称轴,但讨论的本质还是区间与对称轴的位置关系,以便确定远近进一步确定函数值的大小。
四、非典型二次函数求值域
1.根式型二次函数
例1、求函数的值域。
解:分析:函数解析式的两项的幂指数分别为和1,存在2倍关系,故可通过换元得到典型的二次函数。令则那么函数变换为典型的二次函数
y=-t+t²+1+1=t²-t+2值域为
2.三角函数型二次函数
例1、求函数y=cos2x+sinx-1的值域,
解:分析:由余弦的倍角公式可知cos2x可用正弦的平方或余弦的平方表示,故可通过换元得到典型的二次函数。令sinx=t∈[-1,1],那么函数变换为典型的二次函数y=1-2sin²x+sinx-1=-2t²+t值域为
例2、求函数 y=sinx+cosx-3cosx·sinx+1的值域。
解:分析:由三角函数关系式sinx+cosx,sinx-cosx,sinx·cosx可已知一个表示另外两个,故可通过换元得到典型的二次函数。令sinx+cosx=t ,那么函数变换为典型的二次函数
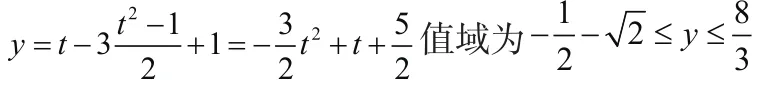
3.指数函数型二次函数
例1、求函数在闭区间[0,1]的值域。
解:分析:由指数的运算性质可知函数的前两项明显存在平方关系,故可通过换元得到典型的二次函数。令那么函数变换为典型的二次函数值域为
例2、求函数的值域。
解:分析:由指数的运算性质可知,由此联想是否也存在平方关系,分析得故可通过换元得到典型的二次函数。令则那么函数变换为典型的二次函数y=t²+t+5值域为
分析:该类型题难度较大,首先综合性强,对高中数学各模块的知识、公式要求熟练掌握;其次是从形式上看具有蒙蔽性,要能通过各种表象看到二次函数的本质。这就要求我们在平时的教学过程中常总结,多归纳。最后只要深入理解并掌握了二次函数几种非常见的形式,都可以通过换元转化为我们熟知的典型二次函数进行求解。
结语
本文主要研究了二次函数在闭区间上值域问题。分类总结了典型与非典型二次函数在闭区间上求值域的方法。二次函数求值域之所以能成为高中数学的重难点并迅速演变为高考的热点,与学生学习二次函数的时间比较分散有很大关系,学生在初中学习了二次函数的基本知识(顶点、对称轴、开口方向等),高一初始学习了二次函数的定义域、值域。然而二次函数在闭区间上的值域考查方式通常和高中数学其它章节的知识点结合起来,以非典型的二次函数出现,综合性较强增加了求解难度。这就要求我们教师上课时要有整体视野,讲到相应的会与二次函数结合的比如向量、三角函数等知识点时,要把相应的新知识与二次函数的结合方式,求解方法讲透彻。在高中课程结束进行一轮复习时,再把所有的非典型二次函数进行一次总结、讲练,相信只要我们教师不断提高自己的业务水平,提升把控教材的视野,很多重难点、高频考点都会有所突破,更容易被学生掌握。
[1]人教A版普通高中数学教材 必修一 人民教育出版社
[2]薜金星 高中数学基础知识手册 北京教育出版社

