直觉主义逻辑上的Friedman-Sheard理论*,†

李晟

四川师范大学 逻辑与信息研究所

四川师范大学 马克思主义学院

nklisheng@126.com

李娜

南开大学 哲学院

linawii@nankai.edu.cn

1 引言

如果一个由若干真之规律（law of truth）组成的集合在经典逻辑上是不相容的，那么是否意味着我们应当拒绝接受它呢？不相容性固然是与真之规律本身的形式有关，但经典逻辑是否也是影响相容性的一个因素呢？对此，利（G.E.Leigh）和拉特延（M.Rathjen）提出了在直觉主义逻辑上重新考察真之规律各种组合的相容性的研究思路（[6]）。我们认为这样的研究思路对于找出导致不相容的原因是很有益的。而且我们认为，不仅是相容性，保守性、组合性等其他真理论性质也可以在新的逻辑上再行检验。这样将有助于真正弄清楚这些性质究竟是基于真之规律本身，还是基于它们的逻辑基础。

我们的方式与利和拉特延的方式有所不同。后者仅仅是以真之规律的组合为对象，他们所关注的焦点在于相容性，其目的是试图为那些不相容的组合寻求适当的辩护。而我们则是以公理化真理论的系统为对象，我们尝试通过将系统原本的经典逻辑基础直接削弱为直觉主义逻辑，从而尝试为研究经典的公理化真理论及其性质提供一种可能的参照。根据这一方式，我们在论文[9]中讨论了两种基于直觉主义逻辑的公理化真理论：IDT和SICT。但是这两种真理论的真谓词都受到了类型的限制，因而具有比较明显的局限性。所以在本文中，我们选择在直觉主义逻辑上重新讨论Friedman-Sheard理论，这是一种无类型的真理论。本文把这一基于直觉主义逻辑的Friedman-Sheard理论记为IFS。我们将首先给出IFS理论的形式系统；然后讨论直觉主义的修正语义学，并证明IFS理论可以将直觉主义修正语义学公理化至第一个极限序数ω；最后简要地讨论IFS理论与它的经典版本FS理论之间的关系。

在接下来的各个小节里，我们用LHA表示海廷算术HA（[8]）的语言，包括逻辑常项¬、∧、∨、→、↔、∀、∃，等词符号=，以及算术符号0、S、+、×。HA是以直觉主义逻辑为基础的，当它被加强为经典逻辑时，所得到的就是皮亚诺算术PA。因此，PA的语言LPA与LHA是完全相同的。如果以一元谓词T扩充LHA，即得到新的语言LT。我们用HAT来命名由LT重新表达后的HA，也即是允许T谓词在HA的归纳公理模式中出现。我们还可以相应地得到PAT。

已知PA有标准模型N（[5]，第10页），它以自然数集N为论域，将算术符号分别解释为自然数0、后继函数、加法函数和乘法函数。根据文献[8]所给出的直觉主义逻辑Kripke模型的构造方法（[8]，第75-87页），我们可以证明K=〈K,≤,N〉是HA的模型。其中，K是一个非空的结点集；≤是结点之间的二元偏序关系；N即PA的标准模型。这意味着当K中只有一个结点时，K与N是相同的。我们用M=〈K,ℑ〉来表示HAT的模型。其中K是HA的模型，ℑ是一个赋值函数，它为每个结点k∈K指派N的一个子集ℑ(k)，作为在该结点上对T谓词的解释，并同时满足条件：对任意结点k和k′，如果有k≤k′，那么有。力迫关系“⊩”按照通常的方式定义（[8]，第80页），但还需增加对T谓词的解释：k⊩T(s)当且仅当sN∈ℑ(k)。sN表示在N中为s指派的值。为使记法简洁，我们将把sN直接记为s。

如果φ是LT的语句，那么┍φ┑表示φ的哥德尔编码。HA原子语句的真谓词在HA中是可定义的公式（[4]，第42页），用V al+(x)表示。此外，SentT(x)表示x是LT语句的哥德尔编码；AtSentT(x)表示x是LT原子语句的哥德尔编码。若将下标“T”换为“HA”或“PA”，则得到相应的HA或PA的句法性质的表达式。三元替换函数x(t/s)表示用项t去替换公式x中的变元s。是自然数n的数字，有时我们也用后继函数来表示。上方加点的逻辑联结词和量词符号用以表示N上的某种特殊的运算，比如：。

2 FS理论的直觉主义版本IFS

2.1 FS理论

哈尔巴赫（V.Halbach）在论文[2]中首次给出了FS理论的公理系统。之所以命名为Friedman-Sheard理论，是因为它等价于弗里德曼（H.Friedman）和希尔德（M.Sheard）在此前的论文[1]中所给出的系统D。下面给出FS理论的哈尔巴赫版本（[3]，第159-161页）：

定义1(FS)FS以LT为形式语言，在PAT的基础上添加下列公理和规则而得到：

（1）公理：

（2）规则：

NEC：对任意LT语句φ，如果能给出φ的证明，那么就能推出T┍φ┑。

CONEC：对任意LT语句φ，如果能给出T┍φ┑的证明，那么就能推出φ。

FS的外逻辑（outer logic）和内逻辑（inner logic）是一致的，也即是构造FS的逻辑基础与FS的T谓词所能作用的语句所遵循的逻辑都是经典逻辑。这是FS最重要的特点。

2.2 直觉主义的IFS理论

定义2(IFS)IFS以LT为形式语言，在HAT的基础上添加下列公理和规则而得到：

（1）公理：

（2）规则：

NEC：对任意LT语句φ，如果能给出φ的证明，那么就能推出T┍φ┑。

CONEC：对任意LT语句φ，如果能给出T┍φ┑的证明，那么就能推出φ。

从表面来看，IFS的真之公理与FS的真之公理并不完全相同，前者增加了关于蕴涵的公理IFS5。这是因为在直觉主义逻辑背景下，逻辑联结词不能相互定义。而在经典逻辑背景下，公理IFS5可以由FS的其余真之公理证明，故而通常将其简化。所以，尽管有公理数量上的不同，但这并不妨碍IFS与FS只在逻辑基础上有区别。

如前所述，哈尔巴赫的FS等价于弗里德曼和希尔德的系统D。通过削弱外逻辑，我们得到了直觉主义的IFS理论，而利和拉特延也按照同样的方式得到了系统D的直觉主义版本Di（[6]）。本文把Di记为IFSO，现在给出IFSO并探讨它与IFS的关系。

定义3(IFSO)IFSO是由下列公理和规则组成：

（1）公理：

（2）规则：T-Intro：对任意LT语句φ，从φ可以推出T┍φ┑；

T-Elim：对任意LT语句φ，从T┍φ┑可以推出φ；

¬T-Intro：对任意LT语句φ，从¬φ可以推出¬T┍φ┑；

¬T-Elim：对任意LT语句φ，从¬T┍φ┑可以推出¬φ。

在定义中，PRE是HA的子理论，它是通过去掉HA的归纳公理模式而得到。Bew(x)表示x是可证语句的哥德尔编码。

定理1IFS⊆IFSO。

证明：只需证明IFSO能够推出IFS的全部真之公理和规则。

验证IFSO⊢IFS1：

因为HA的原子公式与PRE的原子公式是相同的，所以在HA中可以证明下面的这个式子成立：

于是，根据（2-1），一方面有：

以上推理的第二行是因为：HA⊢∀x∀y(¬¬(x=y)→x=y)（[8]，第123-128页）；第三行是依据了PRE的原子语句满足排中律；第四行借助了直觉主义逻辑的有效式，并且其前件可根据PRE-Ref而分离；第五行利用了下述式（2-2）；第六行依赖于事实：HA⊢∀x∀y(x=y→¬¬(x=y))。

同样地，另一方面很容易有：

两个方面相结合，即为IFSO⊢IFS1。

验证IFSO⊢IFS2：

因为¬(φ∧ψ)→(ψ→¬φ)是直觉主义逻辑的有效式，所以从T-Cons可以推出：

与T-Comp(w)结合，即为IFSO⊢IFS2。

验证IFSO⊢IFS3：

一方面有：

另一方面有：

两个方面相结合，即为IFSO⊢IFS3。

其余公理和规则可以类似依次验证。证毕。 □

3 直觉主义的修正语义学

修正语义学（revisionsemantics）是由古谱塔（A.Gupta）和赫兹伯格（H.Herzberger）分别独立提出，并由贝尔纳普（N.Belnap）和古谱塔进一步发展和推广的语义真理论。它是克里普克语义真理论最强有力的竞争者。哈尔巴赫证明了FS与修正语义学的关系，即：FS可以将修正语义学公理化至第一个极限序数ω（[3]）。本节我们将在哈尔巴赫工作1哈尔巴赫在讨论修正语义学时，不仅使用了有别于以往工作的符号和记法，而且提出了一种新的“修正”方式。本文所采用的正是哈尔巴赫记法和方式。的基础上，首先给出标准修正语义学的基本思想和基本结论，然后在直觉主义逻辑的背景下对它们进行推广，并解释直觉主义修正语义学与IFS理论的关系。

3.1 标准的修正语义学与FS理论

修正语义学的基本思想是：从对真谓词的任意解释出发，通过一个恰当的修正过程，得到对该真谓词越来越好的解释。这个恰当的修正过程一般是通过修正算子（revision operator）来定义。

定义4(修正算子) 对自然数集的任意子集S⊆N，修正算子Γ定义为：

，其中φ是LT语句。

在定义4中，N是PA的标准模型，S是修正前对真谓词的解释，Γ(S)是修正后的解释。从该定义可以知道，Γ是N的幂集℘(N)上的运算，并且有：

根据定义4，可以将修正算子的迭代应用Γn(S)定义如下，从而刻画后继序数次迭代的修正过程：

通过上述修正过程，虽然我们能够得到对真谓词越来越好的解释，但是如何理解“越来越好”？这是十分模糊的。而且“越来越好”预设了对真谓词的起始解释也应该是一种“好”的解释，那么如何证明这种解释是好的？这些问题并不容易澄清。因此，哈尔巴赫对关于修正过程的观点做了一些改变。修正过程不再是一个“越来越好”的过程，而是一个从对真谓词的所有可能解释中，逐渐剔除不恰当解释的过程。（[3]，第164-172页）这样一来，N的任何子集都是对真谓词的可能解释，即从N的幂集℘(N)开始，使修正算子Γ作用于℘(N)中的每一个元素，即：

很显然，Γ[℘(N)]是℘(N)的子集。重复上述修正过程，使修正算子Γ作用于Γ[℘(N]中的所有元素，从而得到℘(N)的一个更小的子集。可见，这样的修正过程使得其中一些解释被逐步排除出去。现在，我们可以更一般地将新的修正过程定义如下：

定义5令M⊆℘(N)，并且令Γ[M]={Γ(S)|S⊆M}，那么Γ的后继序数迭代应用Γn[M]就可以定义为：

哈尔巴赫利用这种新的修正过程，解释了FS的子理论（参见定义6）与修正语义学的关系：Γn[℘(N)]的任意元素，都是对FS某个子理论的真谓词的恰当解释，并且这些FS的子理论都有标准模型N。

定义6(FS的子理论) FS的子理论FSn定义如下：

FS0=PAT；

FS1是由FS的所有公理及PAT的整体反射原理2PAT的整体反射原理PAT-Ref，即：∀x(SentT(x)∧BewT(x)→T(x))。组成；

FSn+1的公理与规则同FS并无差别，但是在形式证明中只允许NEC规则和CONEC规则最多应用于n个不同的语句。

定理2对任意n∈N，以及对任意S⊆N，都有：

证明：从左向右，施归纳于FSn证明的长度。从右向左，只需找到一个S′，使得 Γ(S′)=S，并且S′∈Γn-1[℘(N)]（[3]，第 170-172 页）。证毕。 □

3.2 直觉主义的修正语义学

直觉主义修正语义学的思想是：试图把修正语义学与直觉主义逻辑的语义学相结合。斯特恩（J.Stern）在研究模态性与公理化真理论时，定义了一种模态修正语义学，其思想是把修正语义学与模态逻辑的可能世界语义学相结合。（[7]）本文的直觉主义修正语义学正是受到斯特恩的启发。因为直觉主义逻辑的语义学也是一种可能世界语义学，只是在联结词和量词的定义方面与模态逻辑的可能世界语义学有所不同。

定义7(赋值函数) 令K=〈K,≤,N〉是HA的模型，ℑ赋值函数是从结点集K到N的幂集℘(N)的函数，并且满足条件：

其中，ℑ(k)⊆N是ℑ赋值函数在结点k上的值，它表示在结点k上对T谓词的解释。全体ℑ赋值函数的集合记为Vℑ。

定义8(直觉主义修正算子) 直觉主义修正算子Γi是ℑ赋值函数集Vℑ上的运算，使得对任意k∈K，都有：

，其中φ是LT语句。

同样地，Γi的后继序数次迭代定义为：。

直觉主义修正算子的直观含义是：对ℑ赋值函数在每个结点k上为T谓词所做的解释分别进行修正。

推论1对任意LT语句φ，以及对任意结点k∈K，以下等值式成立：

证明：

首先证明“⇐”：因为〈K,ℑ〉[k]⊩φ，由定义 8，┍φ┑∈[Γi(ℑ)](k)，从而得到〈K,Γi(ℑ)〉[k]⊩ T┍φ┑。

然后证明“⇒”：因为〈K,Γi(ℑ)〉[k]⊩ T┍φ┑，于是根据对T谓词的解释可知，┍φ┑∈[Γi(ℑ)](k)，再由定义 8，有〈K,ℑ〉[k]⊩φ。证毕。 □

事实上，根据引理1不难知道如下等值式也是成立的：对任意LT语句φ，〈K,Γi(ℑ)〉⊨ T┍φ┑⇔〈K,ℑ〉⊨φ。

为了表述的方便，下面将以T1┍φ┑ 表示 T┍φ┑，Tn+1┍φ┑ 表示 T┍Tn┍φ┑┑。

定理3以下结论成立：

（1）对任意ℑ1,ℑ2∈Vℑ，如果 Γi(ℑ1)= Γi(ℑ2)，那么ℑ1=ℑ2；

（2）对任意LT语句φ，任意结点k∈K，以及任意n≥1，都有：

（3）对任意n≥1且。

证明：（1）假设，那么存在某个，使得。不妨假设存在LT语句φ，使得，而。即但是。即：。矛盾。

（2）只需对推论1进行迭代即可证得。

（3）因为是一个LT公式，所以由广义对角线引理（[4]，第37页）可知，存在语句λ使得：

因为所以根据（2）可得到如下等值式，对任意结点k∈K，都有：

将(3-1)代入左端，即得：

所以。从而有。 □

事实上，根据推论1和定理3中的（2），我们还可以证明如下推论：

推论2对任意LT语句φ，以及对任意结点k∈K，以下等值式成立：

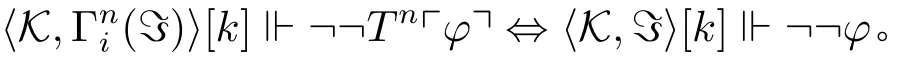
证明：可以通过施归纳于n来证明。首先考虑归纳基始：当n=1时，我们可以建立如下推理：

其次考虑归纳步骤：假设当n≤k时结论成立，现在验证n=k+1的情形：

由此便证明了。 □

以上是直觉主义背景下的“越来越好”修正过程，接下来定义直觉主义背景下的“逐渐排除不恰当”修正过程，也即是允许Γi作用于ℑ赋值函数集Vℑ。

定义9令Γi是直觉主义修正算子，并且令M⊆Vℑ，于是：

Γi的后继序数次迭代应用定义为：。

定理4(Γi的反序性) 对任意m,n∈N，如果m≤n，那么有：

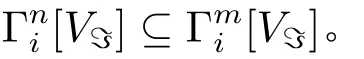
证明：施归纳于Γi的迭代次数k。

归纳基始：当k=1时，结论显然成立。因为根据定义9，，所以很明显；

归纳步骤：假设当k≤l+1时都成立，现在证明k=l+2，即证明：

假设中的任意元素，由定义9可知，存在使得。由归纳假设，，所以，于是按照定义 9，，也即是。 □

Γi的反序性表明，随着Γi的不断迭代，Γi所能作用的赋值函数将会越来越少，并且每一次迭代所排除的都是不恰当的赋值函数。例如，赋值结果包含空集的函数将在第一次迭代后被排除，而赋值结果包含┍T┍0=S(0)┑┑的函数将在第二次迭代后被排除。

推论3 不存在赋值函数ℑ的无穷序列ℑ0,ℑ1,ℑ2,...，使得对任意n∈N，都有 Γi(ℑn+1)=ℑn。

证明：假设存在这样的无穷序列。现在定义一个二元原始递归函数f，使得对任意n∈N，以及对任意LT语句φ，f满足：

f在LT中用符号表示。令ψ(y)表示LT公式，根据广义对角线引理，存在语句λ使得：

很明显，无论对T谓词作何解释，(3-2)都成立。也即是对任意a∈N，都有：

根据⊨的定义不难知道，对任意结点k∈K，都有：

于是对任意结点k1≥k，可以建立如下的推理：

上述推理的第七步与最后一步明显矛盾。而如果假设〈K,ℑa〉[k1]⊩λ，又可以建立如下的推理：

很明显，上述推理的第十二步与最后一步也是矛盾的。

同理可验证，当假设，及假设，也都导致矛盾。所以，任何模型都无法满足(3-3)，因而本引理描述的无穷序列不存在。 □

以上的讨论都是Γi后继序数次迭代应用的情形。现在讨论Γi极限序数次迭代应用，并将第一个极限序数ω次迭代记为：

但是由Γi的反序性可知，Γi的迭代应用不会永恒地进行下去。那么什么时候是尽头呢？下面这个定理将说明，Γi的极限序数ω次迭代应用将是这个尽头。

定理5

证明：假设，也即是存在。于是存在一个赋值函数的无穷序列ℑ0,ℑ1,ℑ2,...，使得对任意n∈N，都有Γi(ℑn+1)=ℑn。但是根据推论3，这样的无穷序列是不存在的。所以。 □

现在建立IFS理论与直觉主义修正语义学之间的核心结论：IFS可将直觉主义修正语义学公理化至第一个极限序数ω。

定义10（IFS的子理论）IFS的子理论IFSn定义如下：

IFS1是由IFS的所有公理及HAT的整体反射原理组成；

IFSn+1的公理与规则同IFS并无差别，但是在形式证明中只允许NEC规则和CONEC规则最多应用于n个不同的语句。

定理6如果令K是HA的模型，Γi是直觉主义修正算子，那么对任意n∈N，下面的等值式成立：

证明：可通过施归纳于n来证明。归纳基始分为两种子情形：

当n=0时：，IFS0=HAT。已知K是HA的模型，并且在HAT中没有真之公理，所以HAT的T谓词不受任何约束，因而Vℑ中的任何ℑ赋值函数都是对HAT中的T谓词的恰当解释；反过来，在每个结点k上任意指派N的一个子集S，只要这些S满足条件，就可以构成一个ℑ赋值函数，由此形成的〈K,ℑ〉一定是HAT的模型，而Vℑ又是所有赋值函数的集合，所以必定有。此种情形得证。

当n=1时：先证明。对任意，可通过施归纳于IFS1证明的长度。只需验证〈K,ℑ〉满足IFS1的真之公理和HAT的整体反射原理。因为，所以存在，使得。

IFS1的验证比较简单，此处从略。

验证IFS2，对任意结点k∈K：

其余联结词和量词公理均可类似验证。现在说明〈K,ℑ〉满足HAT的整体反射原理。因为已经证明了〈K,ℑ′〉⊨HAT，所以根据定义8，对于任意结点k∈K，HAT的所有可证语句的哥德尔编码都在[Γi(ℑ′)](k)中，因而都能为T谓词作用。

再证明。要想证明，也就是要能找到一个，并能证明。现在构造一个函数，使得对任意结点k∈K，都有：

，其中φ是LT语句。

很明显，，现在证明。可以通过对二者中的语句（确切地说，是其元素所编码的语句）的复杂度进行归纳来证明。

对于原子语句T┍φ┑的情形：

对于复合语句¬φ的情形：

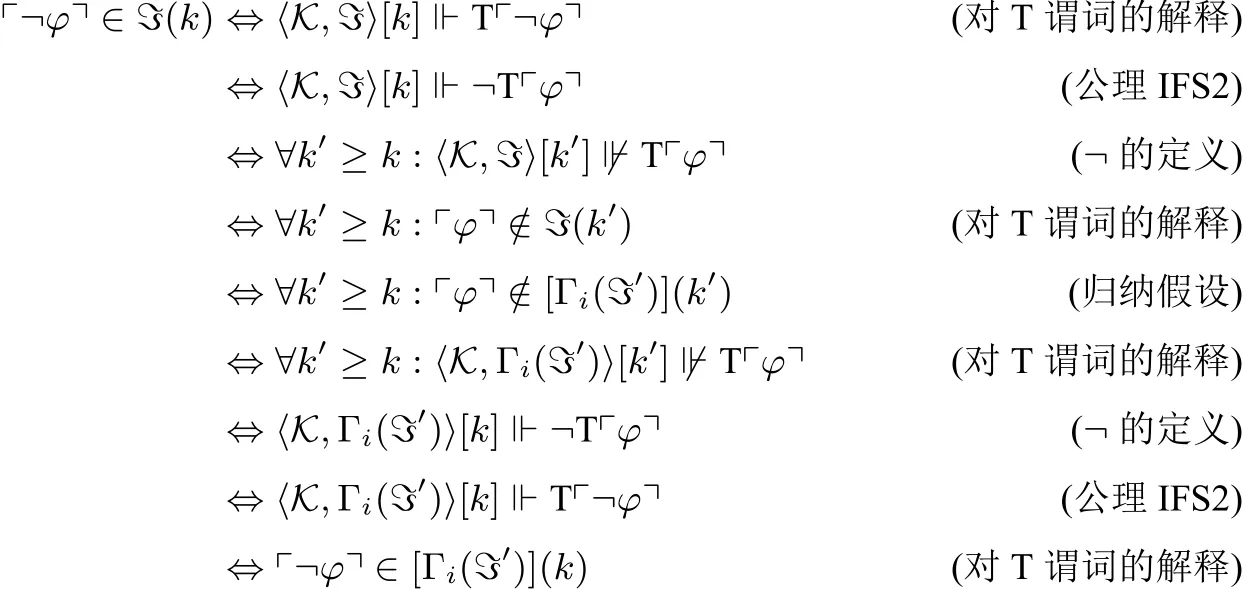
其余联结词和量词的情形类似可证，从而证明Γi(ℑ′)=ℑ。

归纳步骤：假设当n≤k时都成立，现在证明n=k+1。同样分两个方向：

先证明从左到右：也即是假设，证明。根据 Γi的反序性可知，，所以根据归纳假设，〈K,ℑ〉是IFSk的模型，故而只需证明在IFSk中多使用一次NEC规则和CONEC规则可保持〈K,ℑ〉是模型。又因为，所以存在某个，使得。

假设多使用一次NEC规则：

假设多使用一次CONEC规则：

需要注意的是，上述推理从第四步到第五步，是因为ℑ′既属于又属于，而并不是因为可以存在某个ℑ′，使得。而最后一步的得出是因为推理中的ℑ′具有任意性。

再证明从右到左：假设，并且构造一个赋值函数ℑ′，使得对任意k∈K：

，其中φ是LT语句。

由情形n=1的证明可知，Γi(ℑ′)=ℑ。现在只需证明，根据归纳假设，也就是要证明〈K,ℑ′〉⊨ IFSk。

不难知道，对任意LT语句φ，如果IFSk⊢φ，那么只需对φ再使用一次NEC规则即可推出 T┍φ┑，也即是IFSk+1⊢T┍φ┑。于是根据假设就有〈K,ℑ〉⊨ T┍φ┑。又因为已经证明 Γi(ℑ′)=ℑ，所以，，即对任意k∈K，都有。根据推论 1可以得到，。从而也就证明了。 □

推论4IFS是相容的。

证明：对任意LT语句φ，如果IFS⊢φ，那么在对φ的证明中必定只包含有穷多次使用NEC规则和CONEC规则，也就是存在某个子理论IFSn⊢φ。对任意的赋值函数ℑ，都有，于是由定理6可知，即为IFSn的一个模型，所以任何IFSn都是相容的。 □

推论4说明了IFS的相容性。因为定理5表明，当Γi通过极限序数次迭代应用之后，已经不存在恰当的ℑ赋值函数，所以IFS不能证明包含T谓词超穷迭代的语句。也即是，IFS本身没有基于K的算术模型。这与经典的FS理论的结论是完全相同的。

定义11（ω-不相容性）算术理论S是ω-不相容的，当且仅当存在一个公式φ(x)，使得：

（1）S⊢¬∀xφ(x)；

（2）对任意n∈N，都有S⊢φ()。

定理7IFS是ω-不相容的。

证明：定义原始递归函数f=(n,φ)，参见推论3。根据广义对角线引理：

现在建立如下IFS推理一：

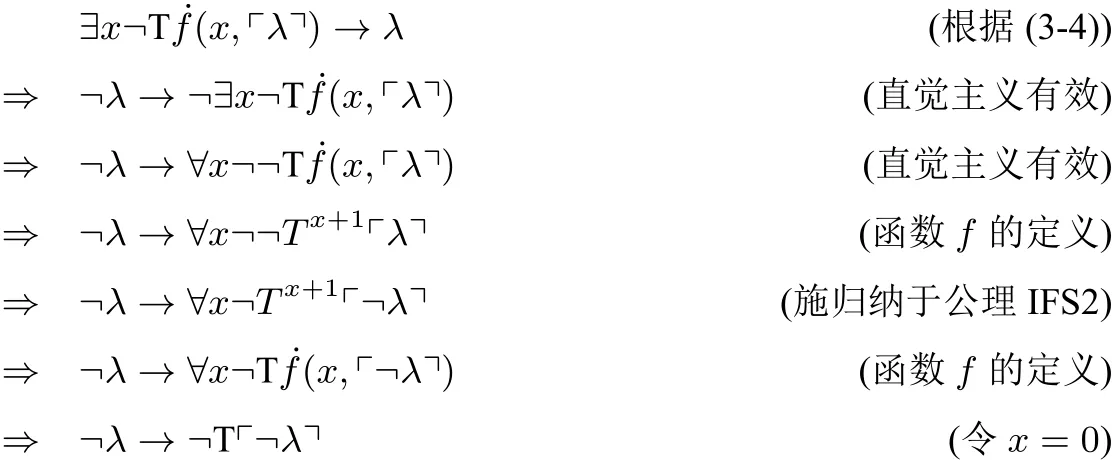
此外，还可建立如下IFS推理二：

推理一与推理二相结合就得到：

如果不断地由(3-5)使用NEC规则，则不难得到如下无穷序列：

这也就说明，对任意n∈N，都有。将其与(3-6)结合，即可证明IFS是ω-不相容性的。 □

FS的最大不足在于ω-不相容性，虽然它并不等同于FS自身的不相容，但是作为一种真理论，这是很难让人接受的。因为FS是ω-不相容的，也就意味着FS不适合PA的标准解释。这就说明当T谓词被添加到PA后，彻底改变了PA原有的意义。而现在看来，这一不足与FS的逻辑基础无关。总之，IFS基本上保持了FS的主要性质。下面简要分析其原因。

4 FS与IFS的关系

已经知道，HA一方面是PA的子理论，但另一方面，PA也可通过否定性转换（negative translation）嵌入HA（[8]，第128页）。FS与IFS之间也有这样的转换。在已有的转换条款的基础上，我们可以定义：

定义12(真理论的否定性转换) 真理论的否定性转换是在PA到HA的否定性转换的基础上，增添如下一条关于T谓词原子语句的转换条款：

定理8 FS⊢φ⇔IFS⊢φ∗。

证明：只需从两个方向分别验证该结论对任意逻辑公理、算术公理以及真之公理都成立。从右向左是显然的，下面只证明从左向右。逻辑公理和算术公理的情形，参阅[8]。

验证IFS2*，：

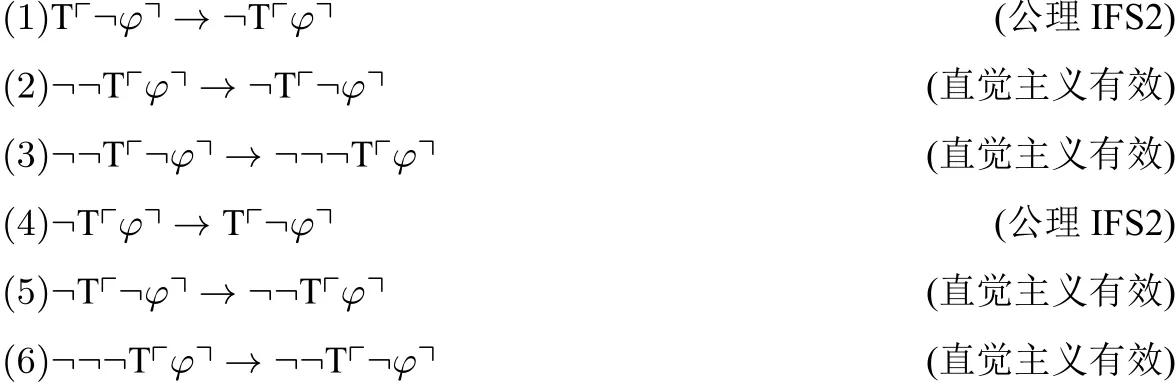
故而；

验证 IFS4*，：

同理可验证，；

验证 IFS7*，：

同理可验证，；其余真之公理可类似验证。 □

定理8表明，IFS之所以能够保持FS的性质，乃是因为我们可以通过否定性转换，把关于FS的性质的结论转换为关于IFS的性质的相应结论。而这也就说明，FS的基本真理论性质主要是基于其真之公理，而不是逻辑基础。

5 结语

在本文中，我们讨论了基于直觉主义逻辑的Friedman-Sheard理论IFS。我们的目的是为研究FS提供一个参照，所以我们建立的IFS理论仅仅是在逻辑基础上与FS不同，而并非按照FS的框架讨论了基于直觉主义的真之规律的新的公理化真理论。我们还讨论了直觉主义修正语义学，它是把标准的修正语义学推广至多个结点而得到。因此当结点集K中只含一个结点时，我们的直觉主义修正语义学就等同于标准的修正语义学。我们证明了IFS能将这样的直觉主义修正语义学公理化至第一个极限序数ω，这是本文最重要的结果。本文最后一个定理的证明表明，FS的性质是由真之规律本身而不是由逻辑基础决定的。

[1]H.Friedman and H.Sheard,1987,“An axiomatic approach to self-referential truth”,Annals of Pure and Applied Logic,33:1-21.

[2]V.Halbach,1994,“A system of complete and consistent truth”,Notre Dame Journal of Formal Logic,36:311-327.

[3]V.Halbach,2011,Axiomatic Theories of Truth,Cambridge:Cambridge University Press.

[4]L.Horsten,2011,The Tarskian Turn:Deflationism and Axiomatic Truth,Cambridge:MIT Press.

[5]R.Kaye,1991,Models of Peano Arithmetic,Oxford:Clarendon Press.

[6]G.E.Leigh and M.Rathjen,2012,“The Friedman-Sheard programme in intuitionistic logic”,Journal of Symbolic Logic,77(3):777-806.

[7]J.Stern,2014,“Modality and axiomatic theories of truth I:Friedman-Sheard”,The Review of Symbolic Logic,7(2):273-298.

[8]A.S.Troelstra and D.van Dalen,1998,Constructivism in Mathematics,Amsterdam:North-Holland.

[9]李娜，李晟，“直觉主义逻辑上的公理化真理论”，逻辑学研究，2015年第3期，第48-63页。