Nonlocal Nonlinear Schrödinger System with Shifted Parity and Delayed Time Reversal Symmetries∗
Cong-Cong Li(李聪聪),Qian Xia(夏骞),and Sen-Yue Lou(楼森岳),2,†
1Center for Nonlinear Science and Department of Physics,Ningbo University,Ningbo 315211,China
2Shanghai Key Laboratory of Trustworthy Computing,East China Normal University,Shanghai 200062,China
1 Introduction
As is well known,there are many events may be happened at different space-times which are correlated and/or entangled.[1]For example,in quantum physics,the state of one particle(A,Alice event)will affect the state of the other(B,Bob event),[2]say,B=A for suitableoperators.Usually,we denote theoperators as the parity(P),time reversal(T),charge conjugation(C),shifted-parity(,x→ −x+x0,where x0is an arbitrary constant),delayed time reversal(,t→ −t+t0,where t0is an arbitrary constant)and their possible combinations.Furthermore,we can apply these symmetries and the AB-BA equivalence principle to describe two-place physical problems,namely,Alice-Bob(AB)systems.[3]In fact,it is far away from the event A happened at{x,t}to the event B happened at{x′,t′}=.Therefore,the Alice-Bob systems are nonlocal.
The study of non-locality can be traced back to the work of Ablowitz and Musslimani.[4]In 2013,Ablowitz and Musslimani investigated an integrable nonlocal nonlinear Schrödinger(NLS)equation
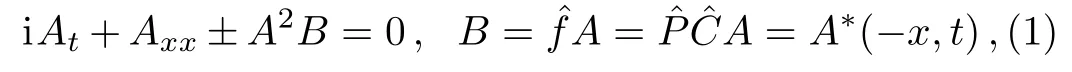
where the operatorsandare the usual charge conjugation and parity.Based on the idea of Ablowitz and Musslimani in Ref.[4],many authors have proposed and studied some other types of two-place nonlocal models.For instance,the nonlocal KdV systems,[5]the nonlocal modified KdV systems,[6−8]the coupled nonlocal NLS systems,[9]the nonlocal Davey-Stewartson systems,[10−12]and the discrete nonlocal NLS systems,[13]etc.
In this paper,inspired by Lou’s work,[3,14]we construct and study the following ABNLS equation
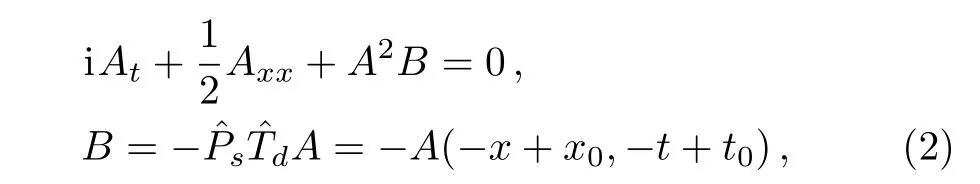
which is shifted parity-time reversalsymmetric.PT-(or PC or PCT)symmetry is a powerful method for the research of physics especially in particle physics and in integrable systems.[15−16]In recent years,a lot of work has devoted to investigating PT-(or more precisely PCT-)symmetry.[17−19]In addition,in Ref.[14]Lou established a general AB-KdV equation and obtained its,,andinvariant multiple solitons,Painlevé II reduction and soliton-cnoidal periodic wave interaction solutions.However,it is still challengeable to seek,and C symmetry breaking solutions.
The paper is organized as follows. In Sec.2,we mainly construct a special ABNLS system and its N-th Darboux transformation through a reduction of the wellknown AKNS system.[20]In Sec.3,we try to investigateand C symmetry breaking solutions with aid of the N-th Darboux transformation of the ABNLS equation.The properties of these solutions are quite different from those for the usual NLS equation.Finally,summary and discussion are provided in Sec.4.
2 The Darboux Transformation for the ABNLS Equation
Darboux transformation has become the most direct and yet important approach in many areas of mathematical physics.It can be used to construct exact and explicit solutions of integrable nonlinear systems,including solitons,breathers,rogue waves,and so on.In this section,we will give the n-fold Darboux transformation for the ABNLS equation(2).Based on the n-fold Darboux transformation,we can achieve new solutions from old ones by simple iteration.It was shown in Ref.[21]that the ABNLS equation possesses the following linear spectral problem:

where λ is a complex spectral parameter.The compatibility condition of Eq.(3),

leads to Eq.(2).
Next,let us take the gauge transformation,

Then,spectral problem(3)is converted into
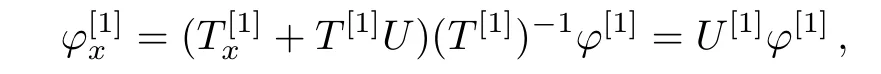
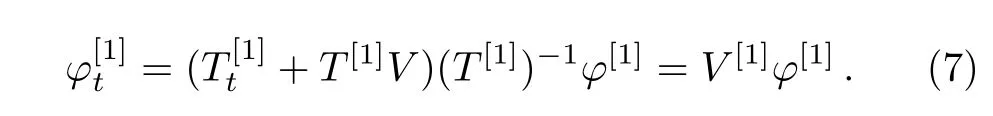
We can find such a fact that U[1]and V[1]are of the same form as U and V with old potentials{A,B}replaced by new potentials{A[1],B[1]}.In general,we suppose
where(i,j=1,2)are functions of x and t need to be determined.Correspondingly,the relation of new and old potentials is given by

According to the correlation relation B=A=∓A(−x+x0,−t+t0),we obtain
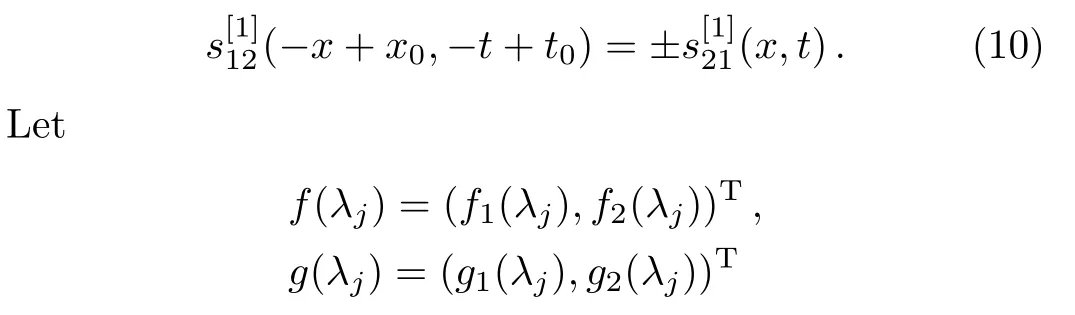
be eigenfunctions associated with the eigenvalue λ = λjin Eq.(3).Then,there exist constants γj(j=1,2)meet the following equations
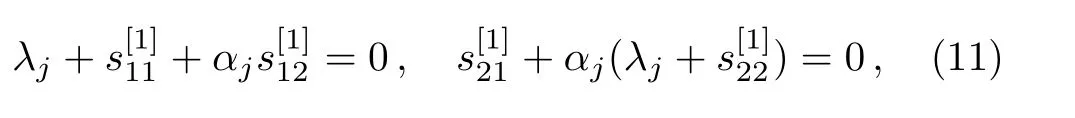
with
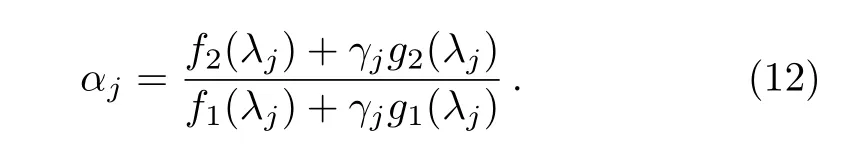
Hence,the matrix T[1]can be rewritten as
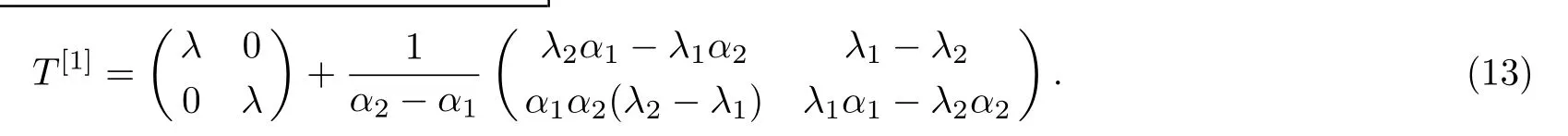
This is the first order Darboux transformation.Further,we will illustrate the n-fold Darboux transformation of the ABNLS equation(2).According to the analysis for T[1],the n-fold Darboux transformation should have the form
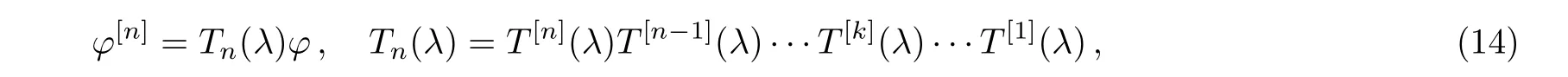
with
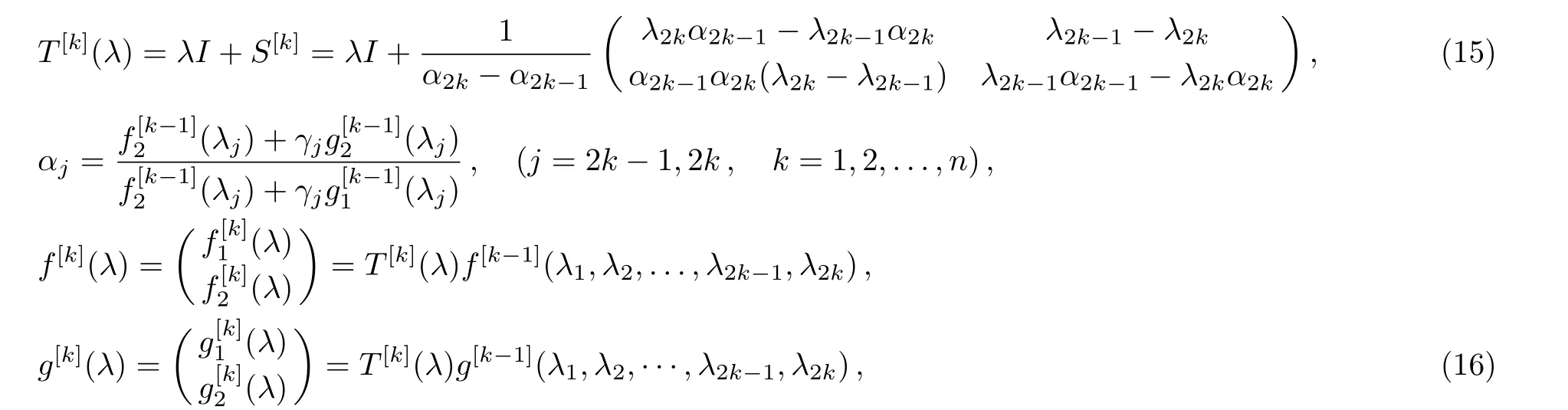
where the constraint condition(10)becomes

Finally,we can get the new solution A[n](x,t),which expressed by

3 Exact Solutions for the ABNLS Equation
In this section,we will devote to study the symmetry breaking solutions of ABNLS equation(2)from Darboux transformation given in the last section,including solitons,rational solitons,complexitons,kinks,antikinks,and rogue-waves.
3.1 One-Soliton Solutions from Zero Seed by Darboux Transformation
We first set seed solution A=0,then by solving the spectral equation(3),we can get two eigenfunctions

corresponding to the eigenvalue λ.
Substituing Eq.(19)into Eq.(12)leads to
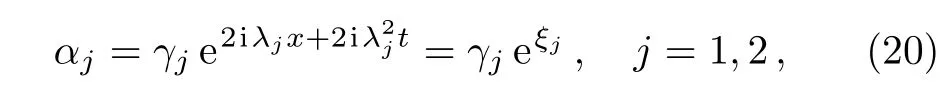
and αjsatisfy Eq.(11),thus,we derive
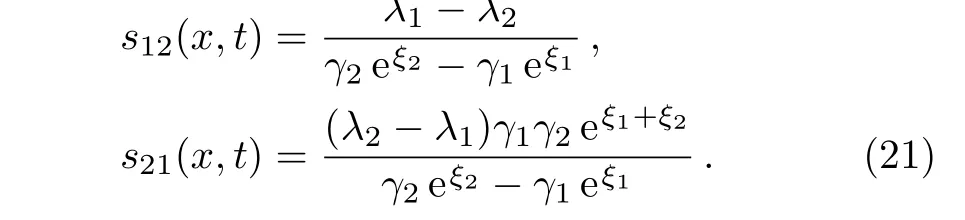
The constraint condition(10)gives rise to

with
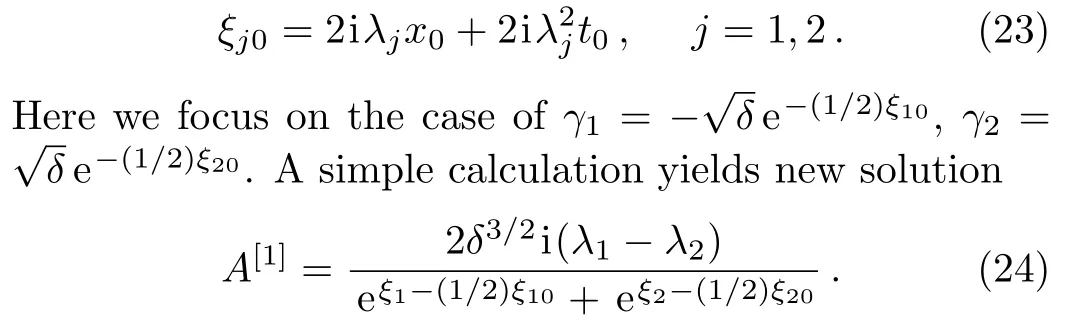
In fact,the one soliton solution possesses some different kind of soliton structures dependent on the parameter selections.
Denote λj= µj+iνj, µj, νj∈ R(j=1,2).Letµ1= µ2and ν1= −ν2,then a typical soliton can be written
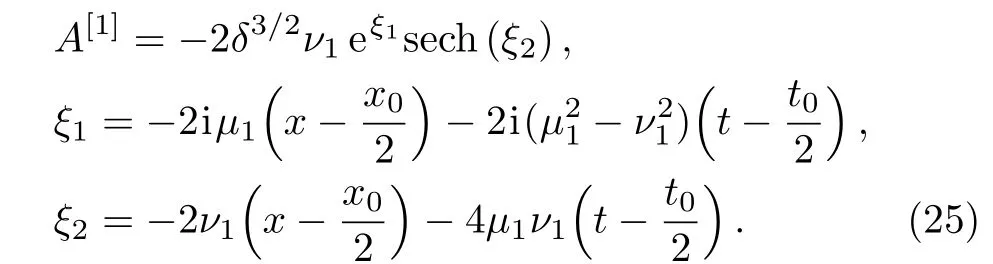
Figure 1 demonstrates this one-soliton solution for the quantity AB.
For the general parameters,the solution(25)is a complexiton solution.Usually,the complexiton solution(25)is singular at the space-time points(n=0,±1,±2,...)

A special complexiton solution(25)is shown in Fig.2.Figure 2(a)is a density plot of the real part of the complexiton with the parameter selectionsµ1=0.2,µ2=0.4,ν1=0.1,ν2=0,δ=1,and x0=t0=0 while Fig.2(b)is the three-dimensional plot of the compexiton with the same parameters as those of Fig.2(a).
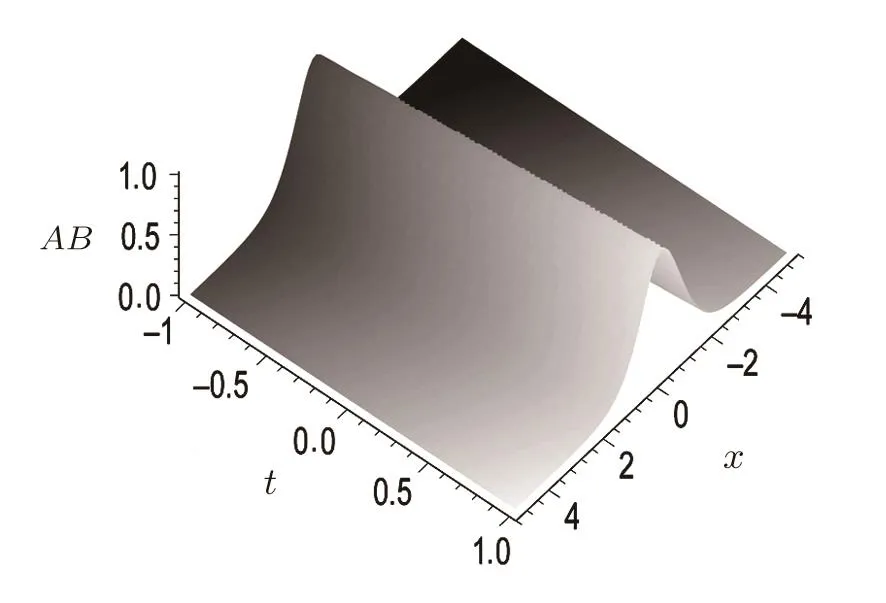
Fig.1 Soliton solution given by Eq.(25)withµ1=µ2=0.2,ν1= −ν2=0.5,δ=1,and x0=t0=0 for the quantity AB.
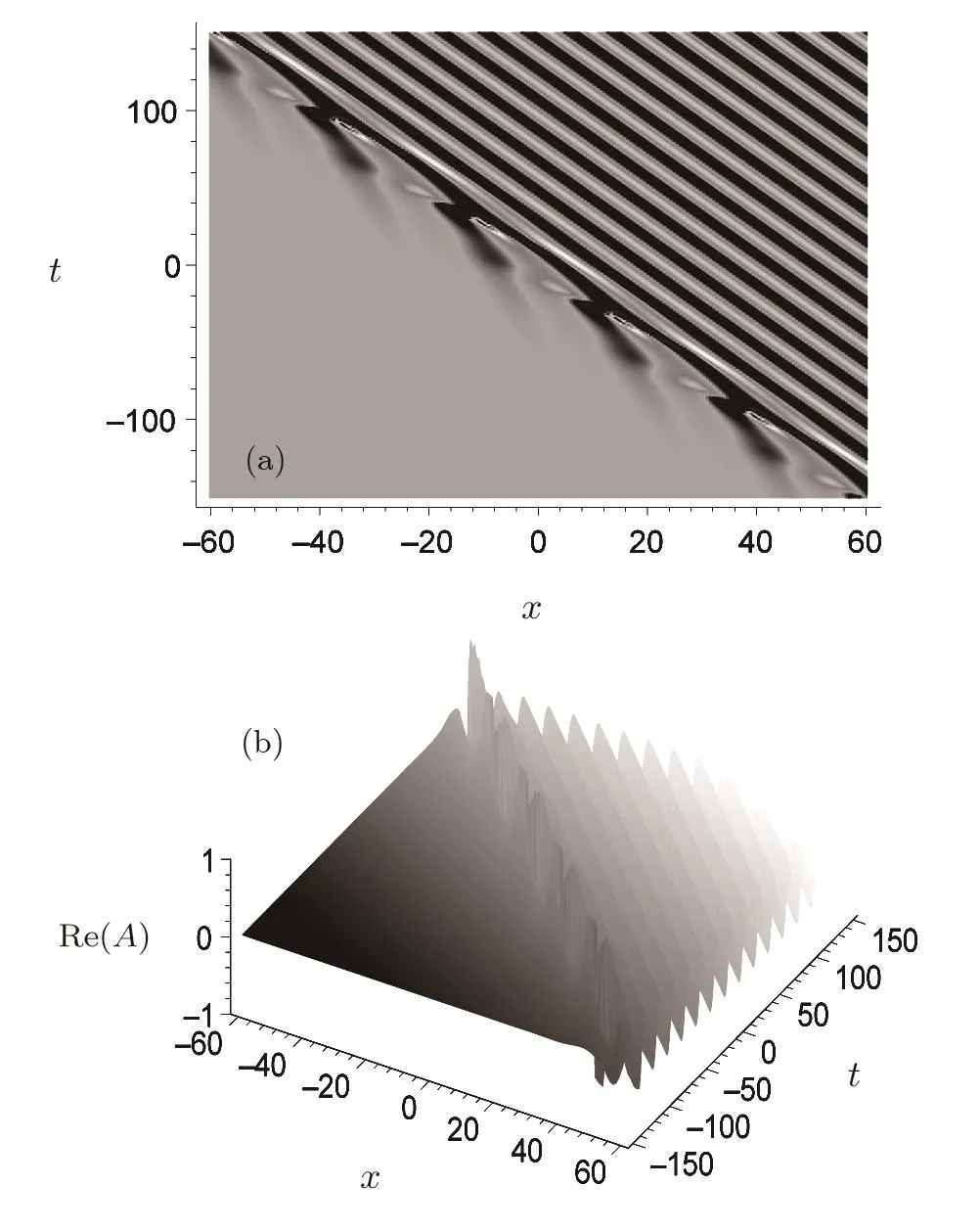
Fig.2 Complexiton solution given by Eq.(25)withµ1=0.2,µ2=0.4,ν1=0.1,ν2=0,δ=1,and x0=t0=0 for the quantity AB.
3.2 One-Soliton Solutions from Nonzero Seed by Darboux Transformation
In this subsection,we mainly study the solutions of the ABNLS equation generated from a nonzero seed.In fact,suppose nonzero seed
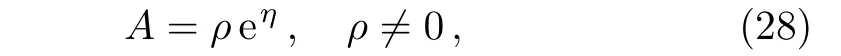
with
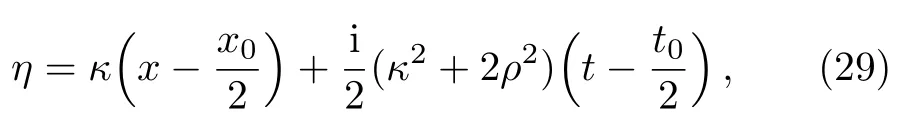
where ρ and κ are two arbitrary complex parameters.
Let λ1=(i/2)(κ +2ρ),the eigenfunctions associated with λ1are
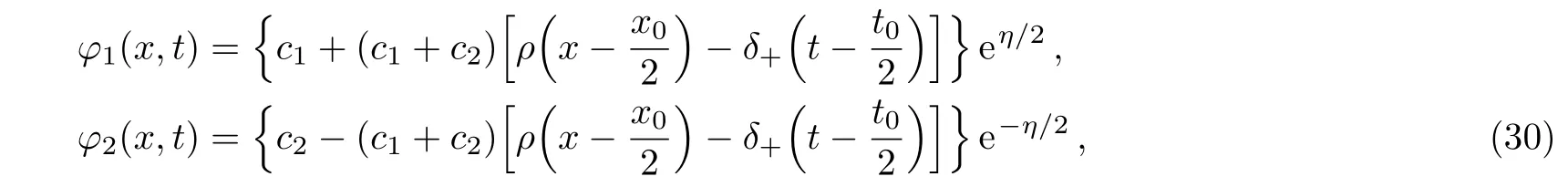
with c1and c2being arbitrary constants and

In the conditions of c1=1 and c2=0,by a direct calculation,we have
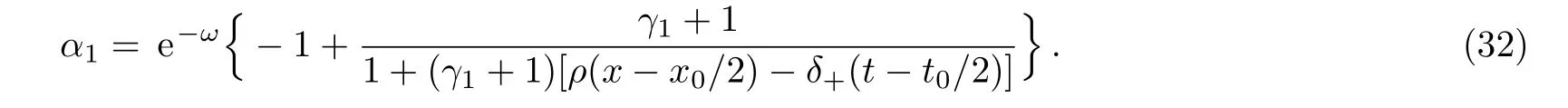
When λ2=(i/2)(κ − 2ρ),solving the spectral problem(3)corresponding to the eigenvalue λ2,we construct two new eigenfunctions as
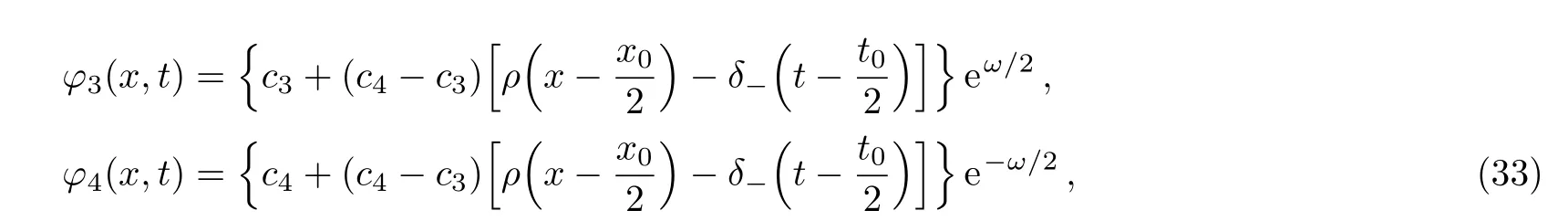
where c3,c4are arbitrary constants and

At the same time,we select c3=0,c4=1,which leads to
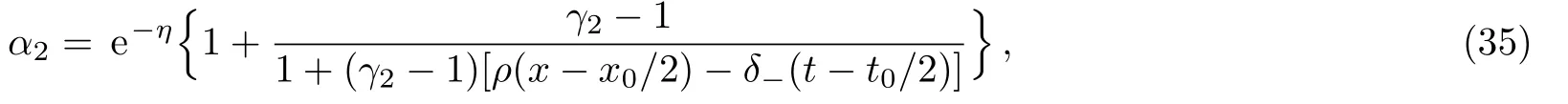

Next,we consider several different solutions arising from Eq.(36)by selecting different parameter selections.
It is not difficult to see that if ρ is real and κ is imaginary,then the solution(36)possesses the rogue-wave form as that of the usual NLS system.Figure 3 demonstrates such a rogue-wave with the choice of parameters ρ= δ=1,κ=i,and x0=t0=0.From the image we can see that an eye-shaped form,which has one high peak and two valleys.
For the ABNLS system,the rogue wave may possess much more abundant structures than that of the usual NLS equation. Figure 4 shows a different rogue wave structure,which possesses also one high peak but possesses more than two valleys.The parameters of Fig.4 are selected as δ=1,ρ =1−0.1i,κ =0.1+i,and x0=t0=0.
For the general selections of the parameters with the conditions

the solution(36)is a singular rogue wave if
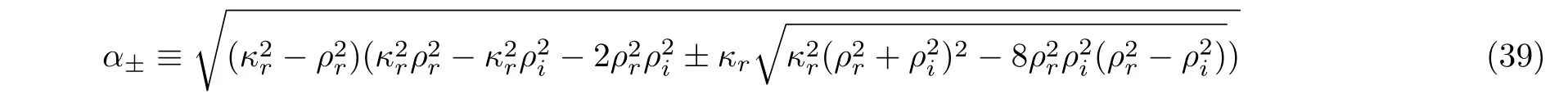
are real at least for one of α+and α−,where the real parameters κr, κi, ρr,and ρiare related to the complex κ and ρ by κ = κr+iκiand ρ = ρr+iρi.The singularities appeared at four possible space-time points
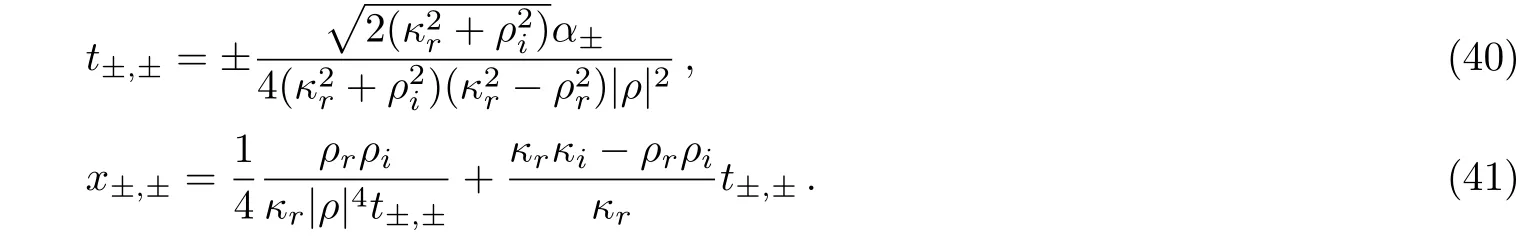
If both α+and α−are complex,then the expression(36)is an analytic rogue wave.
For the special cases related to Eqs.(37)and(38),the nonsingular conditions for the rogue wave(36)read
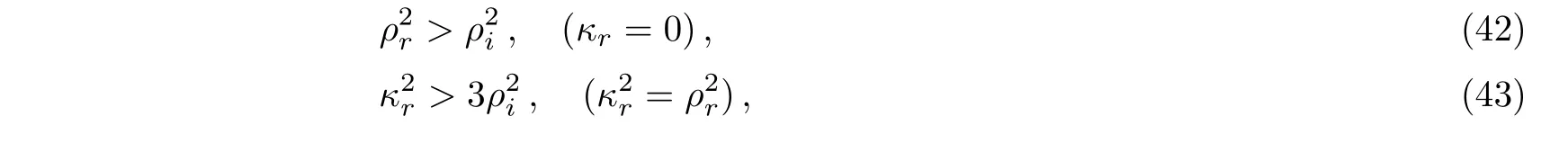
respectively.
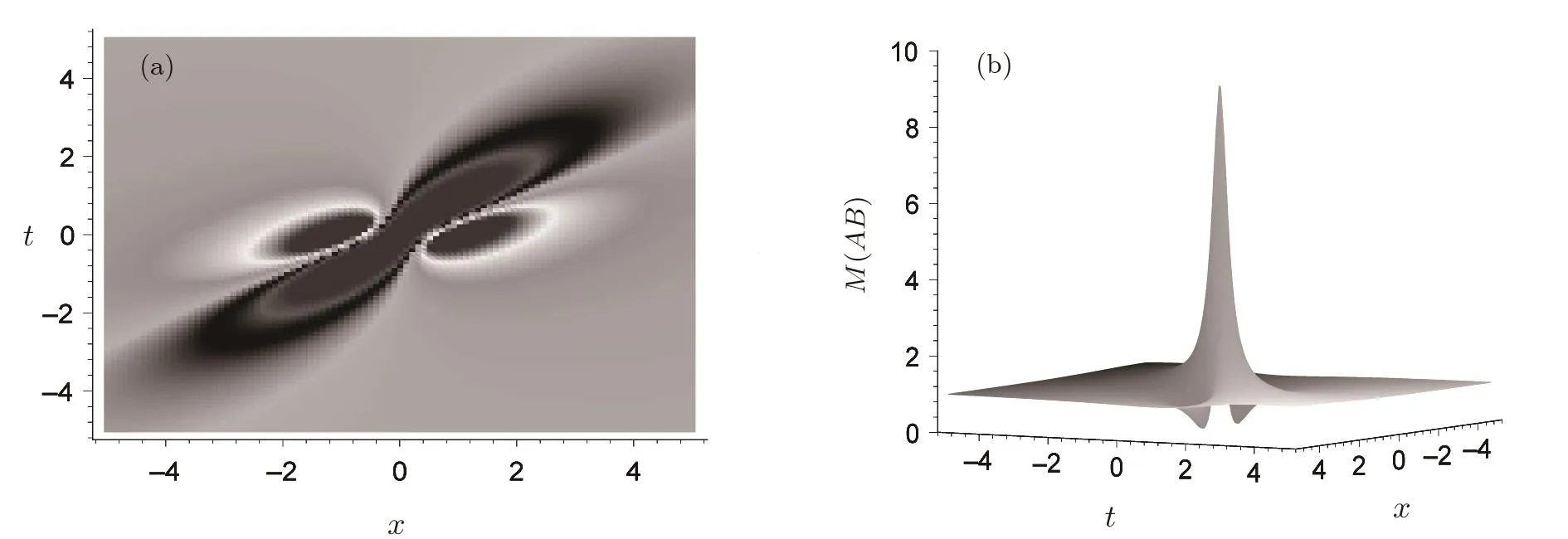
Fig.3 Rogue wave structure expressed by Eq.(36)with µ1=0.2,µ2=0.4,ν1=0.1,ν2=0,δ=1,and x0=t0=0 for the quantity AB.
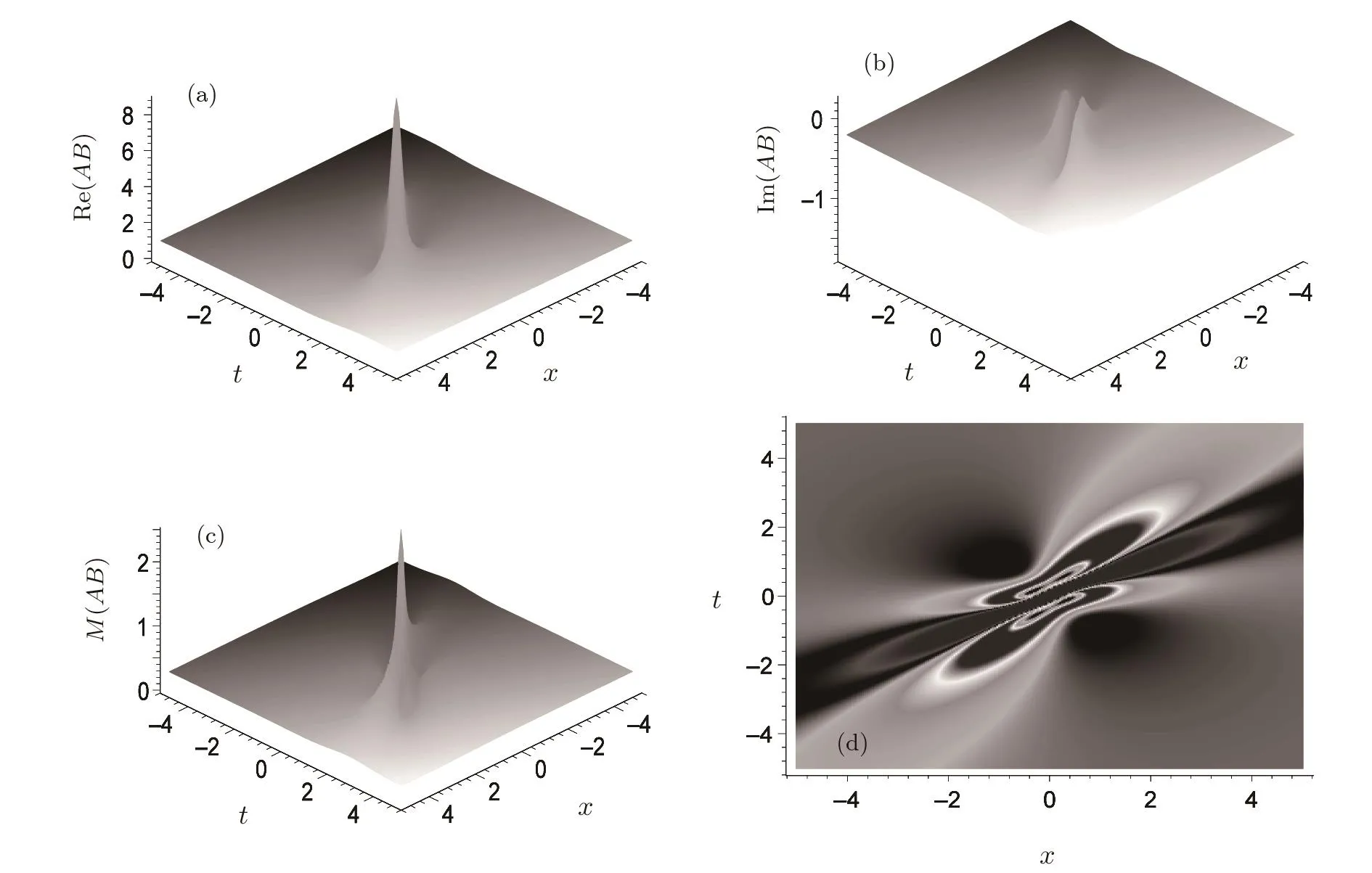
Fig.4 Novel type of rogue wave structure described by Eq.(36)with µ1=0.2,µ2=0.4,ν1=0.1,ν2=0,δ=1,and x0=t0=0 for the quantity AB.
3.3 Two-Soliton Solutions from Zero Seed by Darboux Transformation
Based on the 2-fold Darboux transformation,the two-soliton solutions of ABNLS equation(2)can be easily obtained.First,we denote zero seed A=0.Secondly,from the constraint condition(17),it can be derived that γ1= − e−(1/2)ξ10,γ2=e−(1/2)ξ20,γ3= −e−(1/2)ξ30,and γ4=e−(1/2)ξ40.After finishing complicated calculations,we can get the “two”-soliton solution in the form
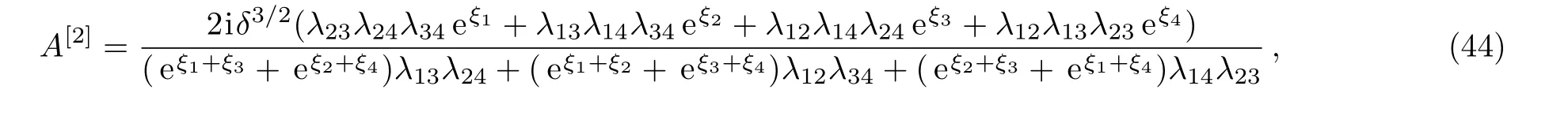
with four arbitrary complex spectral parameters λj,j=1,2,3,4,and

Because of the existence of four arbitrary spectral parameters in Eq.(44),the structure of the “two” soliton solution is quite rich.
The solution(44)may be the usual two interaction solitons as shown in Fig.5 with the parameter selections

The solution(44)may be a breather as shown in Fig.6 with the parameters
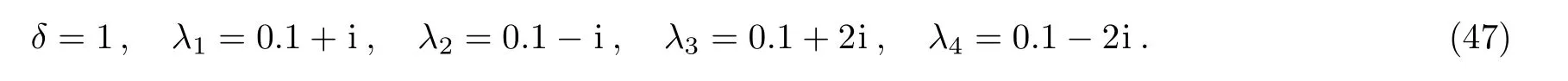
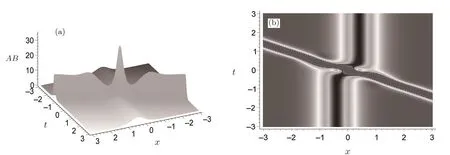
Fig.5 Density plot(a)and three-dimensional plot(b)of the two-soliton solution described by Eq.(44)with the parameter selections(46)for the quantity AB.
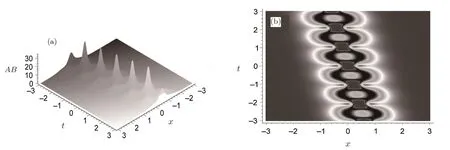
Fig.6 Three-dimensional plot(a)and density plot(b)of the breather solution described by Eq.(44)with the parameter selections(47)for the quantity AB.
The solution(44)may also be the interaction solutions among solitons and(singular)breather as shown in Fig.7 where the parameters are fixed as
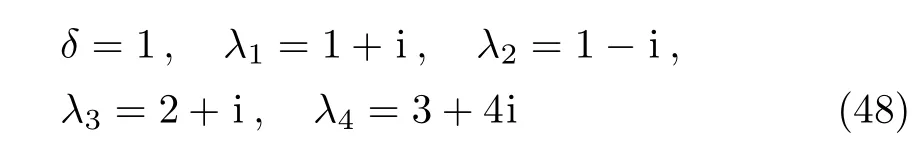
for Fig.7(a)and
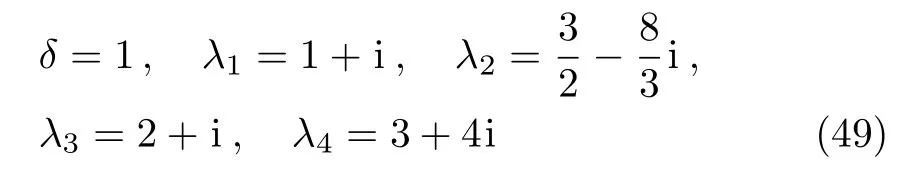
for Fig.7(b).
Figure 7(a)denotes of the interaction between one analytic soliton and two singular breathers while Fig.7(b)exhibits the interaction among three singular breathers.
4 Summary and Discussion
In this paper,we have proposed and researched an ABNLS system,which can be derived from a reduction of the usual AKNS system.In fact,the AB systems are important in describing two-place physical problems.[14]Firstly,we have established an N-th Darboux transformation for the ABNLS equation.Secondly,we have constructed solutions in explicit forms for the ABNLS equation with aid of the Darboux transformation.Thirdly,it is found that the solutions of the ABNLS possess much abundant structure than those of the usual NLS system.Even for the “one” and “two” soliton solutions we can find many kinds of interesting structures,such as solitons,complexitons,rogue-waves(rational solutions),twosoliton solutions,breathers,and the interaction solutions among solitons and breathers.Finally,the different structures of the localized solutions mentioned above are plotted in Figs.1–7 with suitable parameter selections.

Fig.7 Density plots(a)between one analytical soliton and two singular breathers,and(b)among three singular breathers for the “two” soliton solution(44)with the parameters(49).
Acknowledgments
The authors are indebt to thank Prof.Y.Chen and B.Li for their helpful discussions.
[1]J.E.Overland,Physics Today 69(2016)38.
[2]O.Hosten,N.J.Engelsen,R.Krishnakumar,and M.A.Kasevich,doi:10.1038/Nature 16176(2016).
[3]S.Y.Lou,Alice-Bob Aystems,Ps-Td-CPrinciples andMulti-SolitonSolutions,arXiv:1603.03975v2.nlin.SI(2016).
[4]M.J.Ablowitz and Z.H.Musslimani,Phys.Rev.Lett.110(2013)064105.
[5]M.Jia and S.Y.Lou,Phys.Lett.A 382(2018)1157.
[6]M.J.Ablowitz and Z.H.Musslimani,Nonlinearity 29(2016)915.
[7]J.L.Ji and Z.N.Zhu,J.Math.Anal.Appl.453(2017)973.
[8]J.L.Ji and Z.N.Zhu,On a Nonlocal Modified Kortewegde Vries Equation:Integrability,Darboux Transformation and Soliton Solutions,Prepint(2015).
[9]C.Q.Song,D.M.Xiao,and Z.N.Zhu,Commun.Nonlinear.Sci.Numer.Simulat.47(2017)1.
[10]M.Dimakos and A.S.Fokas,J.Math.Phys.54(2014)081504.
[11]A.S.Fokas,Phys.Rev.Lett.96(2006)190201.
[12]A.S.Fokas,Nonlinearity 29(2016)319.
[13]M.J.Ablowitz and Z.H.Musslimani,Phys.Rev.E 90(2014)032912.
[14]S.Y.Lou,Alice-Bob Physics,Coherent Solutions of Nonlocal KdV Systems,arXiv:1606.03154v1.nlin.SI(2016),Sci.Rep.7(2017)869.
[15]P.J.Olver,Applications of Lie Groups to Differential Equations,Springer,New York(1993).
[16]G.W.Bluman and S.Kumei,Symmetries and Differential Equations,Springer,Berlin(1989).
[17]R.El-Ganainy,K.G.Makris,D.N.Christodoulides,and Z.H.Musslimani,Opt Lett.32(2007)2632.
[18]K.G.Makris,R.El-Ganainy,D.N.Chrisrodoulides,and Z.H.Musslimani,Phys.Rev.Lett.100(2008)103904.
[19]C.E.Ruter,K.G.Makris,R.El-Ganainy,et al.,Nat.Phys.6(2010)192.
[20]M.J.Ablowitz,D.J.Kaup,A.C.Newell,and H.Segur,Stud.Appl.Math.53(1974)249.
[21]Tao Yong-Sheng and He Jing-Song,Phys.Rev.E 85(2012)026601.
 Communications in Theoretical Physics2018年7期
Communications in Theoretical Physics2018年7期
- Communications in Theoretical Physics的其它文章
- Electron Correlations,Spin-Orbit Coupling,and Antiferromagnetic Anisotropy in Layered Perovskite Iridates Sr2IrO4∗
- The Three-Pion Decays of the a1(1260)∗
- A New Calculation of Rotational Bands in Alpha-Cluster Nuclei
- Upshot of Chemical Species and Nonlinear Thermal Radiation on Oldroyd-B Nano fluid Flow Past a Bi-directional Stretched Surface with Heat Generation/Absorption in a Porous Media∗
- Detection of Magnetic Field Gradient and Single Spin Using Optically Levitated Nano-Particle in Vacuum∗
- Transverse Transport of Polymeric Nano fluid under Pure Internal Heating:Keller Box Algorithm
