Finsler-Hadwiger型不等式的再加强

李永利

(河南质量工程职业学院　467000)

1　引言

1919年，Weitzenböck给出了如下不等式[1]：

定理1设a,b,c,△分别是△ABC的边长与面积，则

1937年，Finsler和Hadwiger建立了如下一个更强的不等式[2]：

定理2设a,b,c,△分别是△ABC的边长与面积，则

(2)

匡继昌教授在文[3]中总结了近年来对Weitzenböck不等式、Finsler-Hadwiger不等式的一系列研究成果，其中有

定理3[3]237设a,b,c,△,R,r分别是△ABC的边长、面积、外接圆半径和内切圆半径，则

(3)

最近，郭要红、刘其右两位老师在文[4]中对(3)式右端的不等式进行了加强，得到

定理4设a,b,c,△,R,r分别是△ABC的边长、面积、外接圆半径和内切圆半径，则

∑a2-∑(a-b)2

(4)

受文[4]启发，笔者对(3)式左端的不等式也进行了加强，得到如下结果：

定理5设a,b,c,△,R,r分别是△ABC的边长、面积、外接圆半径和内切圆半径，则

∑a2-∑(a-b)2

(5)

2　两个引理

为证明不等式(5)，先给出两个引理．

引理1[3]244(Bottema基本不等式)设a,b,c,p,R,r分别是△ABC的边长、半周长、外接圆半径和内切圆半径，则

p2≤2R2+10Rr-r2+2(R-

其中等号当且仅当三角形为正三角形时成立．

引理2设a,b,c,p,R,r分别是△ABC的边长、半周长、外接圆半径和内切圆半径，则

(6)

其中等号当且仅当三角形为正三角形时成立．

事实上，上式等价于

⟺4R2(R2-2Rr)<(2R2-2Rr-r2)2

⟺4R4-8R3r<4R4+r4-8R3r+4Rr3

⟺r4+4R2r3>0.

而上式显然成立，从而有

于是，由引理1、Euler不等式R≥2r和上式可知

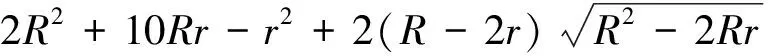
故(6)式成立．由上述证明过程可知，(6)式等号当且仅当三角形为正三角形时成立．

3　结论证明

由文[4]定理的证明过程可知

利用引理2和Euler不等式R≥2r可知

由以上两式可知(5)式成立．至此，定理5得证．

4　注记

注1由定理5和Euler不等式R≥2r可得如下不等式.

推论在定理5的条件下，有

∑a2-∑(a-b)2

(7)

注2显然，引理2中得到的不等式(6)是Gerretsen不等式p2≤4R2+4Rr+3r2的加强．由(6)式和文[4]的引理2可得如下不等式链：

(8)

注3显然(5)，(7)两式是(3)式左端不等式的加强．由(5)式和文[4]的定理4可得如下强于(3)式的不等式链：

≤∑a2-∑(a-b)2

(9)