基于子集重采样的高维资产组合的构建

刘丽萍

（贵州财经大学数学与统计学院，贵阳 550025）

引言

哈里·马科维茨在1952年提出的均值—方差投资组合模型是最为常用的投资组合模型，是现代投资组合理论的基础，该投资组合模型一经提出便得到了广泛的应用。但是，该模型依赖资产间的协方差阵，当资产的维度较高尤其资产的维度大于样本容量时，协方差阵的估计将面临维数诅咒等问题，协方差阵的估计效果较差，从而影响到组合效果。为了解决协方差阵估计所面临的维数诅咒问题，有学者提出了一些方法来估计大维金融资产的协方差阵。Cai和Zhou（2012），Cai和Liu（2011）等将门限方法应用到高维协方差阵的估计中，将一些元素压缩为0来解决维数诅咒问题[1~2]；Fan和Lv（2008）以及Fan和Liao等（2011）将因子分析法应用到大维协方差阵的估计中，通过提取少数共同的因子来解决维数诅咒问题[3~4]；Fan和Liao等（2013）将主成分分析法应用到协方差阵的估计中[5]；Li和 Wang等（2007）将 Cholesky分解法和Lasso方法应用到协方差阵的估计中，来提高大维协方差阵的估计效率[6]；刘丽萍和马丹等（2015）通过在DCC模型中引入主成分正交补门限方法，来估计高维数据的动态条件协方差阵[7]。这些方法都是单纯地从协方差阵估计的角度出发，来解决维数诅咒问题。

另有一些学者考虑通过重采样的方法来解决协方差阵估计的维数诅咒问题，提高投资组合的效率。Michaud（1989）提出，对资产进行抽样，采用样本协方差阵估计方法来估计每次抽取的资产的协方差阵，然后根据均值—方差模型来估计该样本资产的权重，企图获得一个比较稳定的资产分配权重向量[8]。但是，Markowitz和Usmen（2003）以及Wolf（2013）认为Michaud的研究是不稳定的，并没有很好地提高资产组合的效率[9~10]。为此，Fan和Han等（2016）又提出将循环分块bootstrap方法应用到投资组合风险的估计中，来提高组合的效率[11]。

本文在前人研究的基础之上，考虑将子集重采样方法应用到均值—方差投资组合模型中，我们根据Ding和Engle（2001）提出的标量BEKK模型来估计每次抽取的子集的协方差阵[12]，而不是全部资产的协方差阵，所以说一定程度上解决了协方差阵估计所面临的维数诅咒问题，提高了协方差的估计效率。

一、投资组合中大维协方差阵的估计和预测所面临的挑战

（一）协方差阵在投资组合中扮演的角色

协方差阵在投资组合中扮演着重要角色，一般而言，协方差阵的估计越精确，组合的分配越合理。我们以常见的均值—方差投资组合来说明这一问题。均值—方差投资组合的形式为：

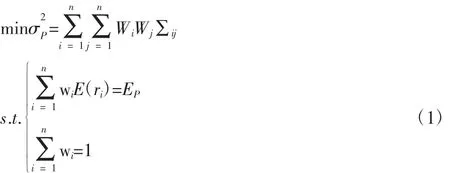
其中，∑ij表示资产间的协方差阵，wi表示投资于第i个资产的权重。可见，投资者购买不同资产的比例或者说权重的分配是依赖于资产间的协方差阵∑ij的。在大维数据背景下，如何估计资产间的协方差阵，是构造投资组合所要解决的关键问题。

（二）样本协方差阵的维数诅咒问题

近年来，随着信息技术的发展，很多企业和金融机构所考虑的资产维度往往较高，甚至超过了其样本容量，此时，高维资产间的样本协方差阵不再是总体协方差阵的一致估计量。根据刘丽萍（2016）的研究[13]，我们通过一个简单的模拟来说明这一问题：假定向量X是从d维的复杂高斯分布中随机抽取的 n个点，即 X～N（0，∑），∑是总体协方差阵，∑=Id，Id是d×d的单位矩阵。假定资产的维度d和样本容量n的关系为：d/n=2，d/n=1，d/n=0.2 和 d/n=0.1。当d=1 000 时，下图给出了总体协方差阵的真实特征值以及样本协方差阵的特征值。

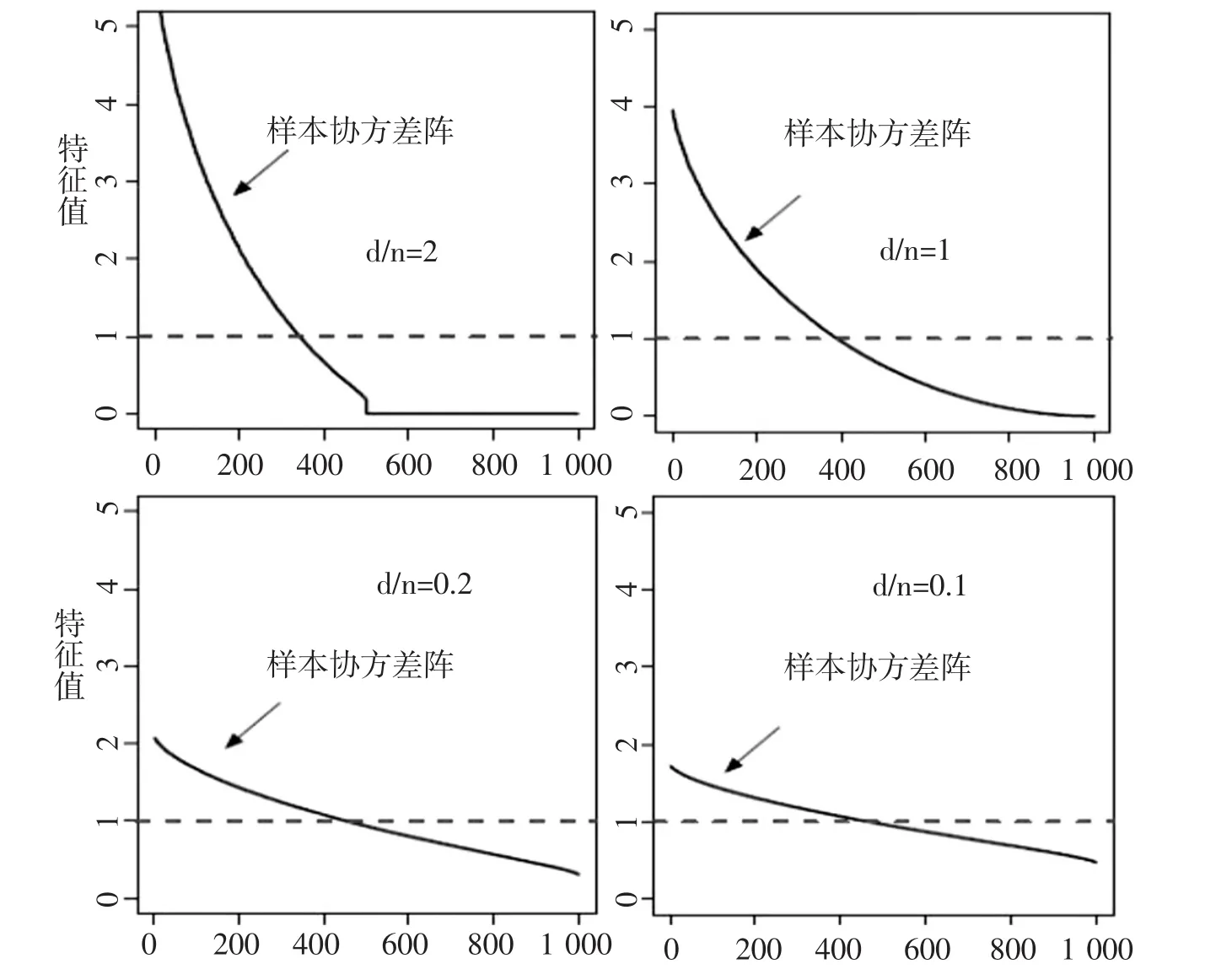
样本协方差阵S（曲线）和总体协方差阵（虚线）的有序特征值图

从上图可知，较样本容量n，资产维度d越大，估计的样本协方差阵的特征值偏离真实的特征值（虚线）越远，样本协方差阵的估计效果越差。实际上，当我们考虑的资产维度较高时，即便选择的样本容量较大，样本协方差阵的估计效果仍不理想。

（三）协方差阵的估计和预测模型（BEKK）所面临的挑战

Ding 和 Engle（2001）提出了标量 BEKK 模型[12]，该模型是常见的协方差阵估计和预测模型，较传统的BEKK模型而言，该模型易于估计，因而被广泛应用。假定资产的维度为k，收益率向量为rt。标量BEKK模型的形式为：

其中，向量ut代表收益率的均值，向量εt代表收益率的残差，It-1代表t-1期的信息集，α、β是标量参数，矩阵∑t为k×k的协方差阵，C为k×k的下三角矩阵。将式（4）两边同时取期望，得：

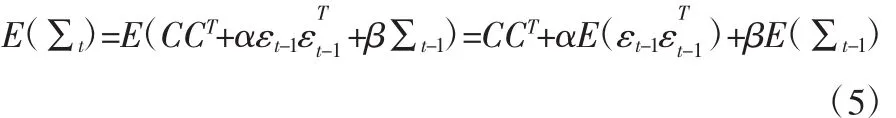
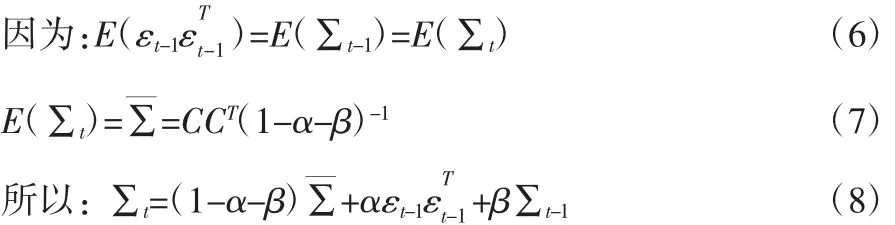
二、基于子集重采样的投资组合

BEKK是常用的用以估计和预测投资组合协方差阵的模型。但是当我们考虑的资产维度较高时，根据前文的研究知其估计效果并不理想。为了提高协方差阵的估计和预测效率，我们考虑将子集重采样方法应用协方差阵的估计中，来提高组合效率。基于子集重抽样的投资组合的思想为：

其一，假定我们考虑的资产维度为n，子集重抽样的思想为：从n个资产中随机抽取b个资产，b是n的子集，b＜n。重复该过程s次，便可以得到s个子集。将子集记为Ij，则对于任意的j=1，…，s，子集的容量。将在第j次抽样中，对应的b个资产的收益向量记为Rj，b。n个资产的收益向量记为R。

其二，采用BEKK模型来估计收益向量Rj，b的协方差阵并根据 Rj，b计算出该子集的平均收益率

其四，对于任意的第 i个资产（i=1，…，n），将其在第 j个子集分配的权重向量记为其中sign（·）是示性函数，当资产i在子集内时

显然，子集的容量b以及抽样的次数s非常关键，会直接影响到协方差阵的估计效率和资产权重的分配。在下文的实证研究中，我们会详细讨论b和s的选择对于组合效率的影响。但是无论如何，采用BEKK模型来估计和预测容量为b的子集的协方差阵时，要比直接估计n个大维资产的协方差阵的估计要好得多，因为b＜n，通过抽取子集，降低了资产的维度，一定程度上解决了维数诅咒问题，提高了协方差阵的估计和预测效率。

三、实证研究

在本文的实证研究中，我们采用了时间区间为2011年1月4日至2014年9月30日的上证180指数成分股数据。将缺失数据剔除后，该区间内共有906个共有交易数据。将长度为906的全样本数据划分为估计和预测两个部分，其中估计区间的长度为806，则预测区间的长度为100。

分别采用BEKK模型和基于子集重采样的BEKK模型（记为BEKKsub）来估计和预测资产的协方差阵，我们采用的滚动估计法，第一次估计时，估计区间为t=1，2，…，806，用该区间内的数据来估计BEKK和BEKKsub模型，并依据该模型预测第807天的协方差阵，根据所预测的协方差阵来构造投资组合，得到该天的组合分配权重和收益。以此类推，最后的估计区间为t=101，102，…，906，重新估计模型并预测资产的协方差阵，进一步得到第907天的组合分配权重和收益。

将采用BEKK模型估计和预测得到的100天的协方差阵代入到前文所述的均值方差投资组合中，得到组合的平均收益为0.0010，组合波动为0.0152，夏普比率值为0.0658。而当采用基于子集重采样BEKK模型，即BEKKsub来估计和预测资产的协方差阵时，子集的容量b以及抽样的次数S会影响到协方差阵的估计效果，并影响到资产组合的收益。为了详细分析b和S对投资组合的影响，我们分别从180支股票中抽取了资产维度为b=10、20、40、60的情况，抽样次数为S=500、1 000、1 500、2 000。下表给出了基于子集重抽样的投资组合的收益、波动以及夏普比率值。

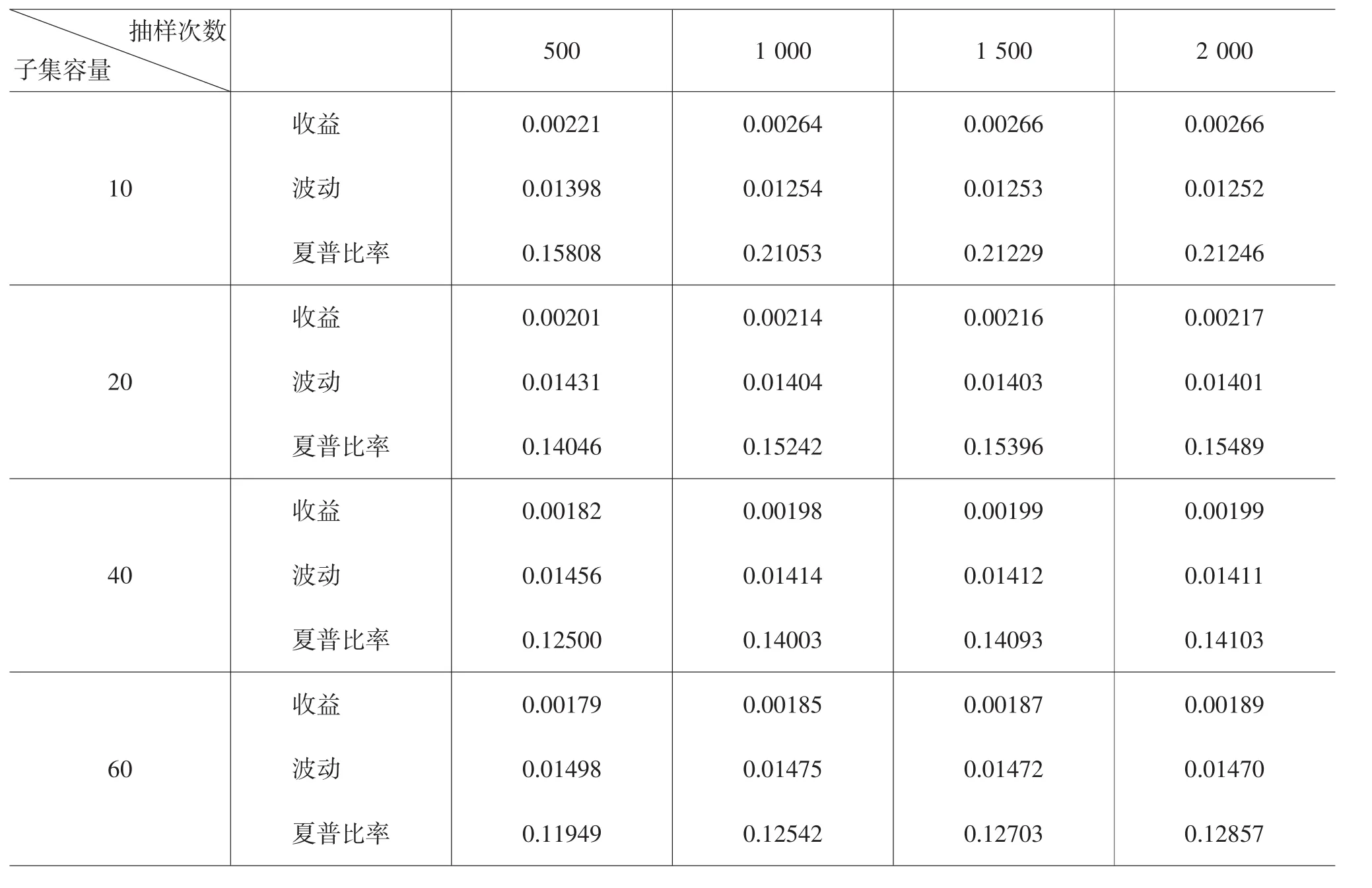
基于子集重抽样的投资组合的收益、波动及夏普比率值

从上页表我们可以得出两条结论：首先，无论子集容量和抽样次数是多少，基于子集重抽样的投资组合明显要优于传统的投资组合，其收益更高、波动更小，并且夏普比率值也较高。这是因为采用BEKK模型来估计和预测容量为b的子集的协方差阵时，因为b＜n，通过抽取子集，降低了资产的维度，一定程度上解决了维数诅咒问题，提高了投资组合的效率。其次，子集容量b对投资组合的效率影响较大。一般而言，子集容量越小，所构造的投资组合的效率越高。而抽样次数对组合效率的影响并不显著，当抽样次数达到1 000时，便会形成比较稳定的投资组合，在此基础上继续增加抽样次数，并不能明显地提高组合效率。

结语

均值—方差投资组合模型是最为常用的投资组合模型，是现代投资组合理论的基础，该投资组合模型一经提出便得到了广泛的应用。但是该模型依赖资产间的协方差阵。在当今大数据时代，高维资产对于很多金融机构非常常见，当资产的维度较高尤其资产的维度大于样本容量时，协方差阵的估计将面临维数诅咒等问题，常见的协方差阵的估计和预测模型——BEKK模型将面临着诸多挑战，估计效果并不理想，从而直接影响到投资组合的效率。为了提高投资组合的效率，本文考虑将子集重采样方法应用到投资组合的构造中，从所有资产构造的集合中抽取若干个子集，然后再采用BEKK模型来估计子集的协方差阵，进一步根据均值—方差模型构造子集的资产组合，最后将若干个子集的同一个资产的权重向量求平均，来求得每个资产的权重。通过实证分析我们发现，基于子集重抽样的投资组合明显要优于传统的均值—方差投资组合，其收益更高、波动更小，并且夏普比率值也较高。