圆锥曲线的弦方程及其应用

浙江省宁波市北仑中学 (315800) 吴文尧

圆锥曲线问题一直是数学高考和竞赛的热点问题，也是高中数学中的难点内容之一,成为难点的其中一个重要原因是过不了“运算关”，常常陷入繁杂的运算而不能自拔,当涉及圆锥曲线的弦时，通常的处理方法是把直线方程代入曲线方程，整理得到一个关于x或y的一元二次方程，从而把问题化归为一元二次方程有关问题来解决，其过程之艰辛大家深有体会.若在解题中能回避把直线方程代入曲线方程，则往往可简化运算过程,笔者发现若在解题中合理地使用圆锥曲线弦所在直线的方程，则能做到这一点.

一、圆锥曲线的弦方程.

1.椭圆的弦所在直线的方程

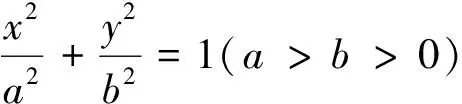
2.双曲线的弦所在直线的方程

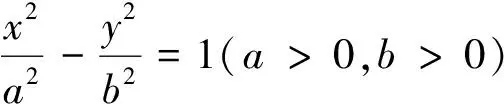
3.抛物线的弦所在直线的方程

说到课桌上睡觉，不是实在犯困，谁能睡得着？睡着了被吵醒，谁能有多少好心情？再说，朦胧中醒来抱怨的一句话，也未必一定是对老师的大不敬，也许，她根本就没弄清楚是谁搅了她的美梦呢？

二、圆锥曲线的弦方程的应用举例

图1

分析：易见本题的本质是一个圆锥曲线中的定点问题，当直线l确定时，整个图形就完全确定，所以按常规的解法，可以设直线l的斜率k为参变量，则点H的坐标(x0,y0)随k的变化而变化，要证明点H为定点，注意到点H在直线x=2y上，所以可“装腔作势”地把点H的纵坐标y0用k表示之，表示以后会发现其值与k无关，要把点H的坐标用k表示之,可以通过把直线l的方程代入椭圆的方程,再运用一元二次方程根和系数的关系建立(x0,y0)与k的关系式,这可是一件很难完成的任务.若利用椭圆的弦方程,则可回避直线方程代入曲线方程.

设M(2cosθ,sinθ)，则直线NM的方程为

评注:注意到R,M,N均是椭圆上的点,上述解法中选择这三点所对应的参数为变量,刚开始共有三个变量,由于直线MN过定点Q,直线RM斜率为定值,由此可减少两个参变量,所以本质上只有一个参变量,当运用条件减少到只含一个参变量时,问题也随之解决了.

图2

分析：由于双曲线关于x轴对称,要证明A和A0关于x轴对称,只须证明这两点的横坐标相等,注意到当直线AB的斜率确定时,A,A0的横坐标也随之确定,故可设法把这两点的坐标用直线AB的斜率表示之.通常方法还是把直线BA方程代入双曲线的方程解决之,但在具体操作中往往陷入繁杂运算而不能自拔,而运用双曲线的弦方程,为我们开启了解决问题的另一扇门.

评注:本题解题思想方法与例1本质上相同,即先选定三个参变量,然后通过运用直线AB,A0B分别过定点F,M减少变量,从而使问题得到解决.

图3

例3 如图3，已知抛物线y2=2px及定点A(a,b),B(-a,0),其中ab≠0,b2≠2pa，M是抛物线上的点，设直线AM,BM与抛物线的另一个交点分别为M2,M1.

证明：当M点在抛物线上变动时(只要M1,M2存在且M1≠M2)直线M1M2恒过一个定点，并求出这个定点的坐标.

分析：要证明动直线M1M2过一个定点，只需写出这条动直线的方程，使其方程中仅有一个参变量.易见动直线M1M2随点M的变化而变化,“照理”可选择点M的坐标作为动直线的参变量，但要把直线M1M2的方程用点M的坐标表示之是件很不容易的事，再注意到M，M1，M2三点的地位等价，且其中一个点确定，另两个点也随之确定，ΔMM1M2三边所在直线方程的写法是一样的，设M(2pt2,2pt)，

从以上三例不难发现,运用曲线的弦方程的解题套路基本相同,即先写出曲线弦的方程,然后利用曲线的弦过某一定点得到相关参数的方程,再运用这个方程达到减少参数目的,从而使原问题得到解决.