Dynamics of Spiral Waves Induced by Periodic Mechanical Deformation with Phase Di ff erence∗
Peng-Fei Li(李鹏飞),Li-Yan Qiao(乔丽颜), Ye-Hua Zhao(赵叶华),,‡ Jiang-Xing Chen(陈江星),and Jun Ma(马军)
1Department of Mathematics,Hangzhou Dianzi University,Hangzhou 310018,China
2Department of Physics,Hangzhou Dianzi University,Hangzhou 310018,China
3Department of Physics,Lanzhou University of Technology,Lanzhou 730050,China
AbstractThe dynamics of spiral waves under the in fluences of periodic mechanical deformation are studied.Here,the mechanical deformation propagating along the medium with phase differences are considered.It is found that weak mechanical deformation may lead to resonant drift of spiral waves.The drift direction and velocity can be changed by the wave length of the deformation.Strong mechanical deformation may result in breakup of spiral waves.The characteristics of breakup are discussed.The critical amplitudes are determined by two factors,i.e.the wave length and frequency of the periodic mechanical deformation.When the wave length of mechanical deformation is comparable to the spiral wave,simulation shows that the critical amplitude is substantially increased.As the frequency of the mechanical deformation is around 1.5 times of the spiral wave,the critical amplitudes are minimal.
Key words:drift,breakup of spiral waves,periodic mechanical deformation,phase difference
1 Introduction
Spatiotemporal patterns arising from reactiondiffusion mechanism are ubiquitous in the nature.[1−3]Spiral waves represent typical two-dimensional spatiotemporal patterns in nonlinear media.Therefore,they have been observed and studied in a wide variety of physical,biological,and chemical far-from-equilibrium systems.[4−9]Wellknown examples include chemical waves in the Belousov-Zabotinsky(BZ)reaction,[10−11]CO oxidation on platinum surfaces,[12]activities of neurons in the brain neural network,[13]and electrical waves in cardiac tissue.[14−15]A major avenue of research is concerned with the formation of spiral waves and the transitions that lead to spatiotemporal chaos,which is principally from the origin of ventricular fibrillation,a lift-threatening arrhythmia.
Due to intrinsic properties of the media,spiral waves have exhibited rich and complicated dynamics.[16−18]The propagation of spiral waves is frequently accompanied by periodic mechanical deformation(PMD)of the medium,which in turns greatly affects their dynamics.It was found that weak PMD may lead to resonant drift if its frequency is equal to that of the spiral wave.[19]In our recent studies,it was shown that the effect of PMD-induced-drift can unpin a spiral wave from an obstacle.[20]On the other hand,strong PMD may result in breakup of spiral waves[21]while a high degree of homogeneous PMD is favored to prevent the low-excitability-induced breakup of spiral waves.[22]Those effects are also reported in mechanoeletrical feedback(MEF)models developed by Pan filov et al.as well as formation of spiral waves.[23]
In the normal physiological situation,the natural pacemaker originates electrical waves of excitation that subsequently propagate through the cardiac tissue. The contraction of a cardiac muscle cell is then caused by its excitation via the process of excitation-contraction coupling.[24]Therefore,the electric waves need time to propagate out,which results in phase differences of mechanical deformation along the cardiac tissue.Despite the rapid progress of mathematical model simulating the activity of PMD,the in fluences of PMD resulting from propagation phase differences have not been explored so far,which makes the studies meaningful.
Here,we address the effects from the phase difference of a PMD on the dynamics of a spiral wave.The drift behavior is in fluenced by the wave length of the PMD.The critical amplitude of the PMD above which the spiral wave breaks up.Two factors are considered,i.e.the wave length and the frequency of the PMD.
2 Model and Method
Our numerical simulations are carried by means of the Bär model based on a two-variable reaction-diffusion equation,[25]which is generally used to describe the excitation dynamics of general excitable media
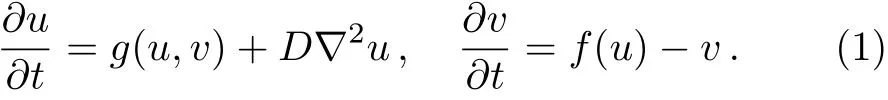
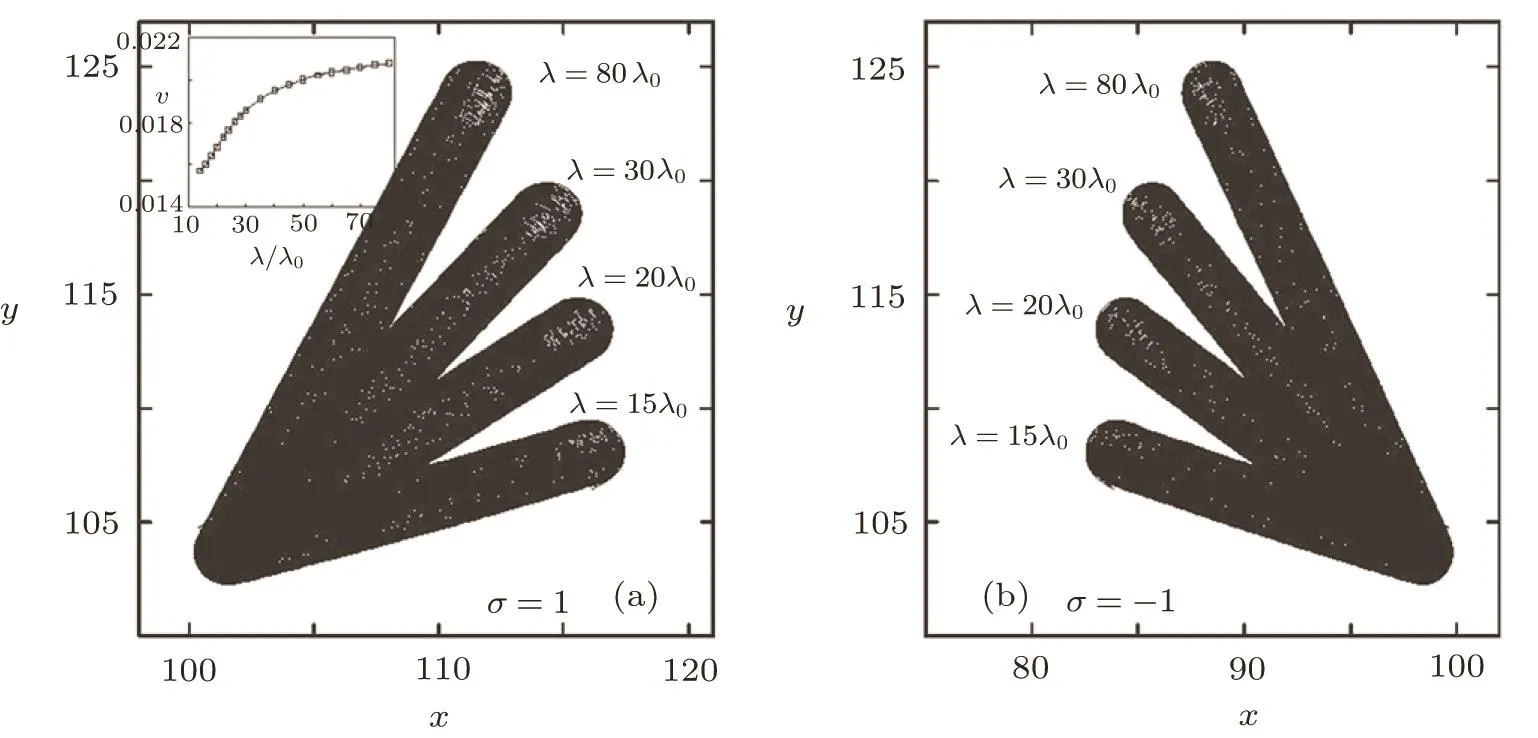
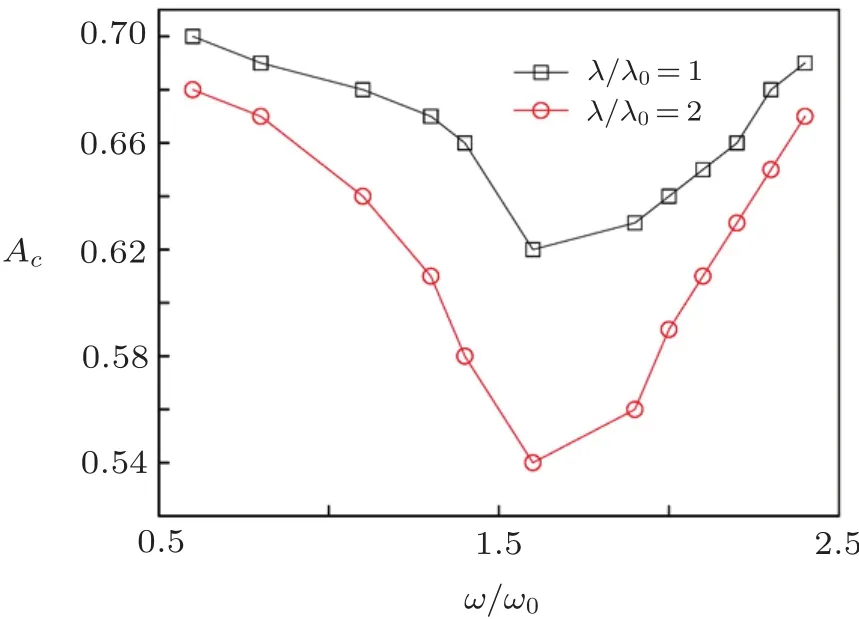
The function g(u,v)takes the form as[u(1−u)/ε][u −(v+b)/a]and f(u,v)is a piecewise function expressed by f(u)=0,if 0≤u<1/3;f(u)=1−6.75u(u−1)3,if 1/3≤u≤1;f(u)=1,if 1 The periodic mechanical deformation of a medium is represented by an operation where any fixed point r of the medium is changed to r′.Here,we consider only one direction(x-direction)and adopt a simple oscillation x′=x[1+Acos(ωdt−2πy/λ+ϕ)]with A the amplitude,ωdthe frequency,and ϕ the initial phase,respectively.The term 2πy/λ denotes the propagation of PMD along the y-direction.Then,Eq.(1)is modified to The 2D system is discretized into 256×256 grids with spacial step ∆r=0.39.Equations(1)–(2)are integrated numerically using the Euler algorithm with time step∆t=0.02.No- flux boundary condition is applied.A spiral wave with frequency ω0and wave length λ0is developed in the system as the initial condition. For a given weak amplitude of the PMD,the system resonates at frequency ω/ω0=1.0,which results in a spiral drift in a straight line.The corresponding trajectories of the spiral tip are shown in Fig.1 where the drift behavior of a counterclockwise and a clockwise rotating spiral wave is presented(σ = ±1 represent the chirality of the spiral,σ=1 for counterclockwise rotating spiral,while σ= −1 for the clockwise one).For a counterclockwise spiral in Fig.1(a),the drift direction changes clockwise when the wave length λ is decreased.The case for a clockwise spiral is opposite,as shown in Fig.1(b).The drift velocity is also in fluenced by the wave length.In the inset of Fig.1(a),we plot the dependence of velocity on the wave length.One can see that the drift velocity of spiral decreases with ω/ω0. Fig.1 (Color online)Dependence of the drift on the wave length(λ/λ0)of PMD at resonant frequency ω/ω0=1.0 for σ=1(a)and σ= −1(b)with A=0.01.The inset shows the drift velocities at different wave lengths. There is a critical curvature Kcabove,which an excitable wave may break up in this local region with subsequent emergence of two free tips.Mikhailov et al.analytically pointed out that the dependence of Kcon the diffusion constant D is Kc∼ D−1.[26]From Eq.(2),one can see that the PMD results in a time-dependent diffusion coefficient,i.e., Consequently,the value of Kcis also time-dependent.When the PMD is applied on the medium,it leads to the deformation of the rotating spiral wave.In Fig.2,a process showing a rotating spiral wave under the in fluences of a PMD with big λ (=14λ0)is presented.At t=8,the spiral wave is deformed,which leads to temporal KT.In this moment,one can find that the wave is flat along the y-direction,which means temporal KTis small.If the amplitude A is big enough and other conditions are suitable,eventually,the temporal KTwill be bigger than time-dependent Kc.Consequently,the spiral wave breaks up,as illustrated at t=12 in Fig.2.A common feature is that the first region where a spiral wave begins to break up locates in the outer spiral arm tangent to the y-axis,which can be seen form the pattern at t=12.The development of breakup reaches a chaotic state at t=90. Then,we decrease the wave length λ to study its in fluence on spiral breakup.In Fig.3,we present the Ac−λ/λ0curves where Acis critical amplitude above which spiral breakup occurs.Three curves are presented to shows cases with different frequencies of the PMD.The changes of Acare not obvious even the values of λ are decreased greatly.However,as the value of λ/λ0approaches around 4.0,the values of Acare increased substantially.Three cases in Fig.3 show this point. Fig.2 (Color online)Evolution of spiral breakup under the in fluence of a PMD with A=0.53,ω =1.5ω0,and λ =14λ0.The spiral wave starts to break up after short time transient rotations.Two free ends appearing at t=12 results in subsequent breakup to a turbulent state at t=90. Fig.3 (Color online)Dependence of critical amplitude of Acabove spiral waves break up on λ/λ0.The triangle,square,and circle curves are plotted from the frequencies with ω/ω0=1.0,ω/ω0=2.0,and ω/ω0=1.5,respectively. To understand the mechanism which underpins the increases of Acas λ is decreased to value comparable to λ0,we present a process of spiral breakup by a PMD with λ =1.0λ0in Fig.4.Note that the amplitude in this case is much bigger than that in Fig.2.Di ff erent from the case in Fig.2,the small λ (1.0λ0)ruffles the spiral wave,which can be seen from the pattern at t=3,8,10.The same as that in Fig.2,the convex part with positive curvature inclines to spiral breakup. However,the concave part of the wave with negative curvature,may increase the velocity of wave propagation according to the relation V=c−DK where c is the velocity of a plane wave.[27]Compared to the cases with big wave length,the presented spiral wave with small wave length shows that the concave part is close to the convex part.Consequently,the convex parts are dragged by the close-by concave parts,which makes it resistant to be broken with bigger Ac.Compared to the case in Fig.2,the time sequence in Fig.4 shows the difference process illustrating the dynamics of spiral breakup. Fig.4 (Color online)Time sequence illustrating the dynamics of spiral breakup induced by a PMD with A=0.64,ω/ω0=1.5,and λ =1.0λ0. Fig.5 (Color online)Dependence of critical amplitude Acon the frequency of the PMD ω/ω0.The square and circle curves are plotted from the wave length λ/λ0=1.0 and 2.0,respectively. The frequency of the PMD(ω)also plays an important role in determining the value of Ac.In Fig.5,we present the Ac−ω/ω0curve with wave length comparable to that of the spiral(λ/λ0=1.0 and 2.0).One can see a tonguelike region in both cases.An interesting point is that Acis smallest when the ω is around 1.5ω0.From the evolution of spiral breakup,simulation shows that the plausible mechanism is that the deformation of spiral wave by PMD is serious at this frequency. In conclusion,we have studied the dynamics of spiral waves induced by periodic mechanical deformation.The phase difference of PMD is firstly introduced.Weak PMD may induce resonant drift of spiral waves.The drift direction changes clockwise for a counterclockwise rotating spiral while the case is opposite for a counterclockwise spiral.The drift velocity decreases with the wave length λ/λ0.It is found that strong PMD results in breakup of spiral waves.The process and underlying mechanism of breakup are discussed.When the wave length of the PMD is decreased to that comparable to that of a spiral,simulation shows the critical value(Ac)of amplitude of the PMD increases substantially.The mechanism is attributed to the appearance of ruffles and consequent dynamics.The frequency of the PMD plays another important role in determining the values of Ac.It is found that the values of Acare smallest when the frequency of PMD is around 1.5 times of the spiral wave.We believe our results can be observed in chemical experiments such as BZ reaction in gels.Furthermore,since our simulation bases on the consideration of realistic conditions in cardiac tissue where the heart is stretching and contracting induced by the pacemaker all the time,we hope our results will contribute to understand the dynamics of spiral breakup in these cases.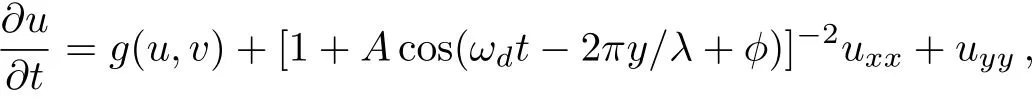

3 Results and Discussion



4 Conclusion
 Communications in Theoretical Physics2018年12期
Communications in Theoretical Physics2018年12期
- Communications in Theoretical Physics的其它文章
- Mixed Local-Nonlocal Vector Schrödinger Equations and Their Breather Solutions∗
- Circular Semi-Quantum Secret Sharing Using Single Particles∗
- Existence and Dynamics of Bounded Traveling Wave Solutions to Getmanou Equation∗
- Runaway Directions in O’Raifeartaigh Models∗
- The 1/NcExpansion in Hadron Effective Field Theory∗
- Quasinormal Modes of the Planar Black Holes of a Particular Lovelock Theory∗
