跳扩散模型下亚式期权定价的柳树法研究

姚 怡，李帅芳，许 威

(同济大学 数学科学学院，上海 200092)

本文在Merton跳扩散模型下，提出了基于柳树结构的定价亚式期权的方法.柳树法[10]最初通过构造离散的马尔科夫过程来刻画几何布朗运动对欧式期权定价.图1展示了一个柳树结构的简单例子.该柳树结构从初始时刻0到T，有5个离散时刻，从第2个时刻起，每个时刻有5个可能的资产价格节点.图1为柳树结构示意图，在实际应用中每一时刻上的资产价格数可以根据模型具体情况任意指定，通常节点个数设为30～50就能够在期权定价问题上保证较高的精度.柳树结构的优点是每个时刻上的资产价格数是常数，因此，随着时间步数的增加，柳树上节点的总个数是线性增长的，而不是二叉树中的平方增长，提高了数值方法的效率.

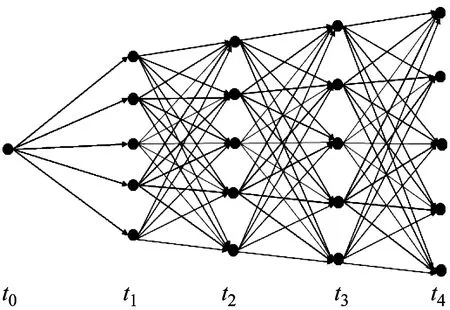
图1 包含5个时刻、5个资产价格节点的柳树结构图Fig.1 Graphical depiction of the willow tree lattice with 5 space nodes and 5 time nodes

在Merton跳扩散模型下，本文提出的柳树构造主要分为两部分：首先在计算对数资产价格四阶矩的基础上，通过Johnson曲线，将服从标准正态分布的离散节点转换成服从跳扩散模型的价格节点，得到了资产价格的估计；然后根据跳扩散模型下资产价格满足的条件概率，推导出每两个相邻时刻间的转移概率公式，并对转移概率做了修正，从而保证资产价格满足鞅的性质，同时提高定价精度.在亚式期权定价过程中，平均价格依赖于价格变化的路径.不同于文献[11]中将所有精确的算术平均价格全部计算出来，本文预先计算出每个时刻平均价格的最大值和最小值，在此区间内通过等差数列选取给定个数的平均价格，而对于没有取到的平均价格节点，通过线性插值即可对其进行定价，以起到减少计算量的作用，从而解决了亚式期权定价中的路径依赖问题.另外，本文分析了柳树法的截断误差和插值误差，证明了柳树法的收敛性.最后，本文针对不同参数下的亚式期权进行了数值实验，并将柳树法结果与蒙特卡洛方法进行比较，数值结果显示柳树法与蒙特卡洛方法有相同的计算精度.由于柳树法存储的平均价格节点个数远少于实际的平均价格路径，从而使得运行时间大大减少.

1 跳扩散模型下亚式期权的柳树法定价

在Merton跳扩散模型下，假设标的资产价格St满足：

(1)

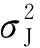
下文通过构造在Merton跳扩散模型下的柳树结构描述资产价格变化的随机过程.构造柳树结构包括两部分：资产价格的估计和转移概率的计算.

1.1 资产价格估计

在Merton跳扩散模型下，基于方程(1)，令X=ln(St/S0)，则时刻t的资产价格St即为St=S0·eX，且满足

根据Ballotta和Kyriakou[12]的推导，可以得到X的期望μ，方差υ，偏度κ3和峰度κ4分别为

(2)

本文在Merton跳扩散模型下，利用Johnson曲线转换公式的逆变换，将一个标准正态分布的随机变量转换成一个满足式(2)中X的四阶矩的随机变量，从而估计资产价格的分布.

Johnson提出的方法[13]可以将任意连续随机变量X转换成正态分布的随机变量Z.其主要原理是通过计算已知变量的四阶矩，然后代入统一的公式中估计该变量的离散值.该模型可以灵活地匹配任意变量的期望、方差、偏度和峰度，并且根据偏度和峰度便可唯一确定模型中所需函数的具体类型.Johnson曲线公式如下：

基于Hill提出的算法[14]，参数a、b、c、d和函数g(·)的类型都可以根据对应随机变量的四阶矩求得.而根据Johnson曲线的逆变换，则可以将一个标准正态分布的随机变量Z转换成给定的分布X，即

(3)

由此，可以利用Johnson曲线的逆变换，得到基于Merton跳扩散模型(1)的资产价格柳树.该算法总结如下：对于一个标的资产，给定其初始价格S0，将时间区间[0,T]划分为N个时间步数，在每个时刻t有m个可能的资产价格，表示为St，且满足公式(1).时刻t的m个离散值可通过以下步骤得到：

步骤1 定义资产回报X=ln(St/S0)，通过式(2)计算X的期望、方差、偏度和峰度.

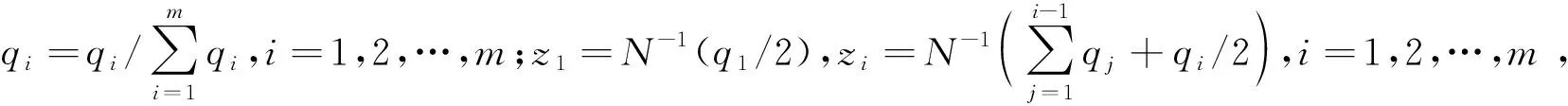
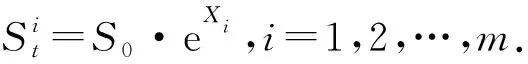
1.2 转移概率计算

在获得资产价格的估计后，本节构造转移概率矩阵来刻画资产价格的变化.假设时刻t的资产价格St已知，则在时刻t+Δt，给定lnSt下的lnSt+Δt的概率密度函数为

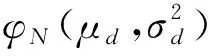
μd=lnSt+(r-ρ-λk-0.5σ2)Δt+dαJ

则对应的累积分布函数为

PJ(lnSt+Δt≤A|lnSt)=

其中，N(·)是标准正态分布的累积分布函数.

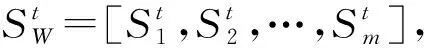
i=1,2,…,m,j=1,2,…,m

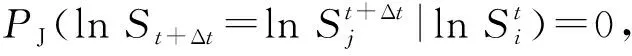
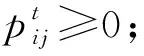
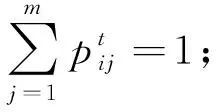
由此，x的表达式如下：

完成以上修正后，即可得到t到t+Δt时刻的转移概率矩阵.

通过资产价格的估计和转移概率的计算，构造了一棵完整的跳扩散模型下的柳树.

1.3 定价跳扩散模型下亚式期权的柳树法

对于平均价格路径较多的问题，本文利用插值技术减少计算量，推导亚式期权定价过程，解决了路径依赖问题.

定义欧式亚式期权的价值为关于S、A和t的函数，即Vc=Vc(S,A,t)，则在跳扩散模型下Vc满足下列积分-微分方程：

(4)

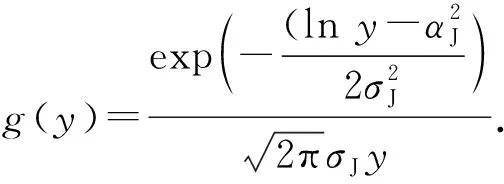
并且存在如下递推公式：

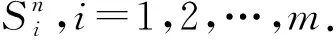
(5)

假设时刻tn，每个价格节点处有ka个平均价格，取等差数列得到

(6)

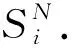
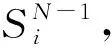
(7)

(8)

i=1,2,…,m,k=1,2,…,ka

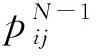
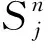
2 误差分析

2.1 柳树法的截断误差

在[tn,tn+1]时间内，由于平均价格A不变，亚式期权价格V满足如下微分方程：

(9)

式中：y服从对数正态分布；g(y)是y的概率密度函数.令X=lnS，η=lny，则dy=eηdη，式(9)作变量代换变为

(10)

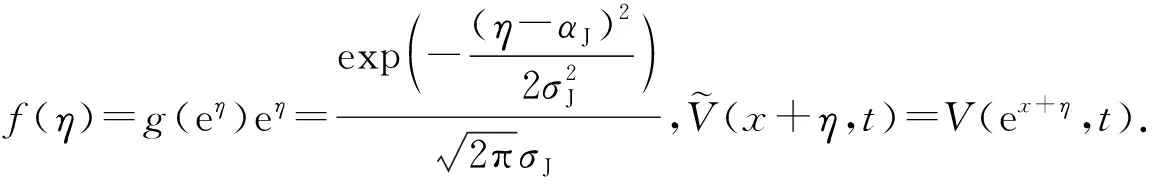
使用柳树法定价时，在tn时刻，亚式期权的价格可以由倒推公式求得，即

(11)

定理1假设资产价格S满足Merton跳扩散模型，由柳树法定价公式(11)计算的期权价值与方程(10)的真实解之间的全局截断误差为O(Δt)+O(E[η5])，即全局截断误差的大小取决于跳扩散中资产价格S的跳跃幅度lny的五阶矩.

证明 在Merton跳扩散模型下，时间区间[tn,tn+1]内下式成立：

(r-σ2/2-λκ+λαJ)Δt

(r-σ2/2-λκ+λαJ)4Δt4

(12)

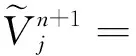
(13)

将式(12)、(13)代入式(11)中，简化之后可以得到

(14)

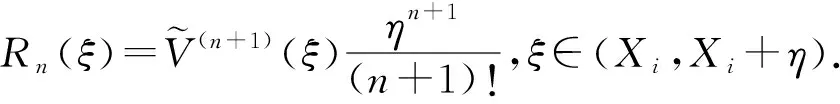
(15)

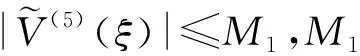
(16)

因此，将式(15)代入式(14)得

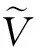
2.2 柳树法的插值误差

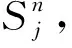
在柳树法中，用线性插值所得期权价值为

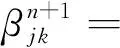
(17)

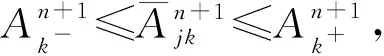
所以

(18)

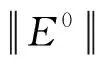
其中：N=T/Δt.若令ka=C·N，C为常数，则‖E0‖I≤O(Δt).因此，柳树法的整体误差为O(Δt)+O(E[η5])，即整体误差的大小取决于跳扩散中资产价格S的跳跃幅度lny的五阶矩.

3 Merton跳扩散模型下亚式期权定价的数值实验

对不同参数的亚式期权进行分析，比较柳树法与蒙特卡洛方法的数值结果.所有数值实验的程序均在操作系统为64位Windows 7旗舰版的计算机上运行，内存为4 GB，处理器为Intel(R) Core(TM) i5-5200U CPU@2.20GHz，使用的软件版本为Matlab R2016a.

实验中，柳树法中资产价格节点个数m=50，平均价格个数ka=0.6N，离散时间步数N为初始时刻距离到期日的天数，蒙特卡洛方法的模拟路径数为2×104.实验比较了不同参数σ、αJ、σJ、λ以及不同到期日T情况下柳树法和蒙特卡洛方法的表现.

首先，固定跳扩散欧式亚式看涨期权的初始价格S0=100，敲定价格K=100，利率r=0.05，跳扩散的频率λ=1，到期日T为90 d.然后选取了不同的波动率σ，Merton跳扩散运动的期望αJ，标准差σJ.从表1可以看出，柳树法的定价结果均落在蒙特卡洛模拟的99%置信区间内，说明了柳树法定价期权的精确性.从计算时间上看，在给定资产价格节点个数m和时间节点个数N时，其他参数的变化并没有影响柳树法的计算时间，跳扩散模型的变化对其计算时间影响很小.但是，柳树法的计算时间则远远小于蒙特卡洛方法.

表1不同σ、αJ、σJ下，柳树法和蒙特卡洛法定价Merton跳扩散亚式期权的结果
Tab.1ResultsofwillowtreemethodandMonteCarlomothedatdifferentσ,αJandσJvalues

σαJσJ期权价值/元时间/s柳树法99%置信区间下界上界柳树法蒙特卡洛法0.20-0.02-0.05-0.100.052.716 72.581 12.720 11.413.20.102.855 52.761 12.910 81.312.70.153.020 92.881 33.048 61.313.10.203.208 63.089 93.299 41.412.80.052.761 62.659 02.798 31.312.70.102.890 92.763 12.900 11.413.30.153.050 42.992 43.160 31.412.30.203.230 23.122 53.317 31.412.80.052.905 52.786 72.930 61.313.30.103.007 22.884 93.032 21.313.20.153.135 93.010 83.169 81.412.50.203.292 13.180 33.359 51.413.50.25-0.02-0.05-0.100.053.280 13.176 73.347 91.413.30.103.400 03.280 63.463 31.413.70.153.569 73.393 53.590 31.412.10.203.755 03.576 43.805 81.312.80.053.320 83.198 33.373 01.312.70.103.431 03.303 93.482 01.413.30.153.578 93.455 93.651 21.312.90.203.758 83.612 93.830 71.312.80.053.442 83.297 73.475 61.313.50.103.527 03.351 03.530 31.313.20.153.564 93.410 93.598 61.412.80.203.815 53.631 93.841 31.413.60.30-0.02-0.05-0.100.053.849 73.679 63.884 81.513.20.103.960 83.754 03.964 31.513.70.154.109 23.982 14.212 91.513.10.204.276 04.153 44.407 51.412.90.053.886 03.708 33.912 31.413.70.103.920 63.733 53.943 51.413.50.154.121 34.016 34.244 11.412.90.204.297 34.101 34.348 01.413.80.053.991 63.848 24.058 41.413.90.104.077 13.895 74.109 41.313.70.154.194 24.041 34.261 71.513.80.204.341 84.157 44.392 81.514.2

接下来，讨论跳扩散模型下跳跃的频率λ对数值结果的影响.令λ=1.5和λ=2.0，在固定σ=0.2,S=100,K=100,T=90 d的情况下，分别考虑不同取值的αJ与σJ，结果如表2所示.表2的结果表明，用柳树法定价的结果完全落在了蒙特卡洛模拟的99%置信区间内，λ的变化并不会影响柳树法定价跳扩散模型下亚式期权的准确性.

表2不同λ下柳树法和蒙特卡洛法定价Merton跳扩散亚式期权的结果
Tab.2ResultsofwillowtreemethodandMonteCarlomothedatdifferentλvalues

σαJσJ期权价值/元时间/s柳树法99%置信区间下界上界柳树法蒙特卡洛法1.5-0.02-0.05-0.100.052.751 82.624 02.763 61.513.20.102.957 82.841 92.998 41.512.70.153.213 63.102 33.291 41.513.10.203.516 93.412 83.646 51.512.80.052.813 72.688 42.849 91.612.70.103.005 62.952 93.105 21.613.30.153.250 83.108 93.288 21.512.30.203.508 73.357 23.572 81.512.80.053.037 02.971 63.122 51.613.30.103.181 13.144 33.301 61.513.20.153.398 43.259 03.417 91.512.50.203.598 73.515 93.719 11.513.52.0-0.02-0.05-0.100.052.785 62.660 52.803 81.513.30.103.058 92.975 23.140 41.413.70.153.404 13.237 03.437 31.512.10.203.802 73.626 43.883 41.412.80.052.874 92.770 92.916 11.412.70.103.129 52.991 03.151 91.413.30.153.444 63.347 63.541 11.312.90.203.793 43.668 73.908 41.412.80.053.174 13.104 23.260 71.413.50.103.342 73.206 53.367 31.413.20.153.578 93.502 73.682 61.512.80.203.899 13.798 04.012 31.413.6

另外，当S0=100时，考虑不同敲定价格对亚式期权定价的影响.针对敲定价格K=90,K=95,K=100和K=105的情形，选取了一组σ、λ、αJ、σJ，分别为λ=1，σ=0.2，αJ=-0.02，σJ=0.05.将对应的期权定价结果和计算时间列于表3.结果说明，敲定价格K的变化不影响柳树法定价亚式期权的表现.定价结果均落在蒙特卡洛模拟的99%置信区间内，而且计算时间也明显少于蒙特卡洛方法.

最后，考虑期权到期日时间的不同对柳树法定价的影响.以上的数值实验都基于期权的到期日为90 d，表4给出了到期日为180 d和365 d的实验结果.结果表明，到期日T的变化不影响柳树法定价亚式期权的表现.定价结果均包含在蒙特卡洛模拟的99%置信区间内，而且计算时间也明显少于蒙特卡洛方法.因此，数值实验表明了柳树法在定价跳扩散模型下的亚式期权具有更明显的优势.

表3不同K下，柳树法和蒙特卡洛法定价Merton跳扩散亚式期权的结果
Tab.3ResultsofwillowtreemethodandMonteCarlomothedatdifferentKvalues

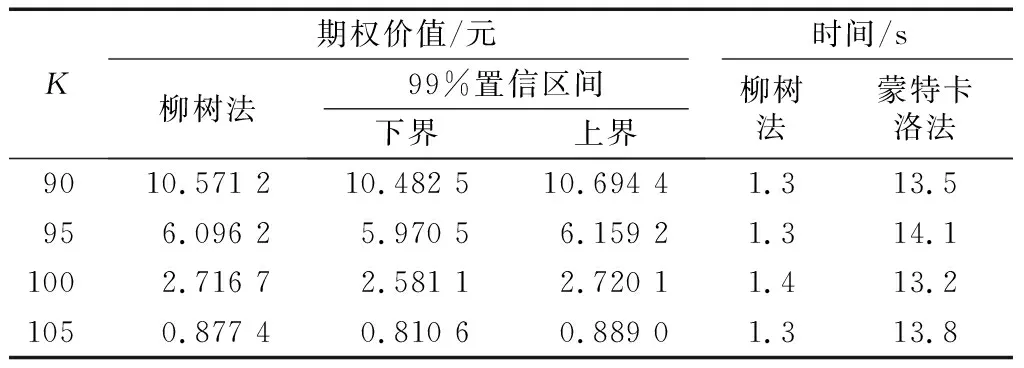
K期权价值/元时间/s柳树法99%置信区间下界上界柳树法蒙特卡洛法9010.571 210.482 510.694 41.313.5956.096 25.970 56.159 21.314.11002.716 72.581 12.720 11.413.21050.877 40.810 60.889 01.313.8

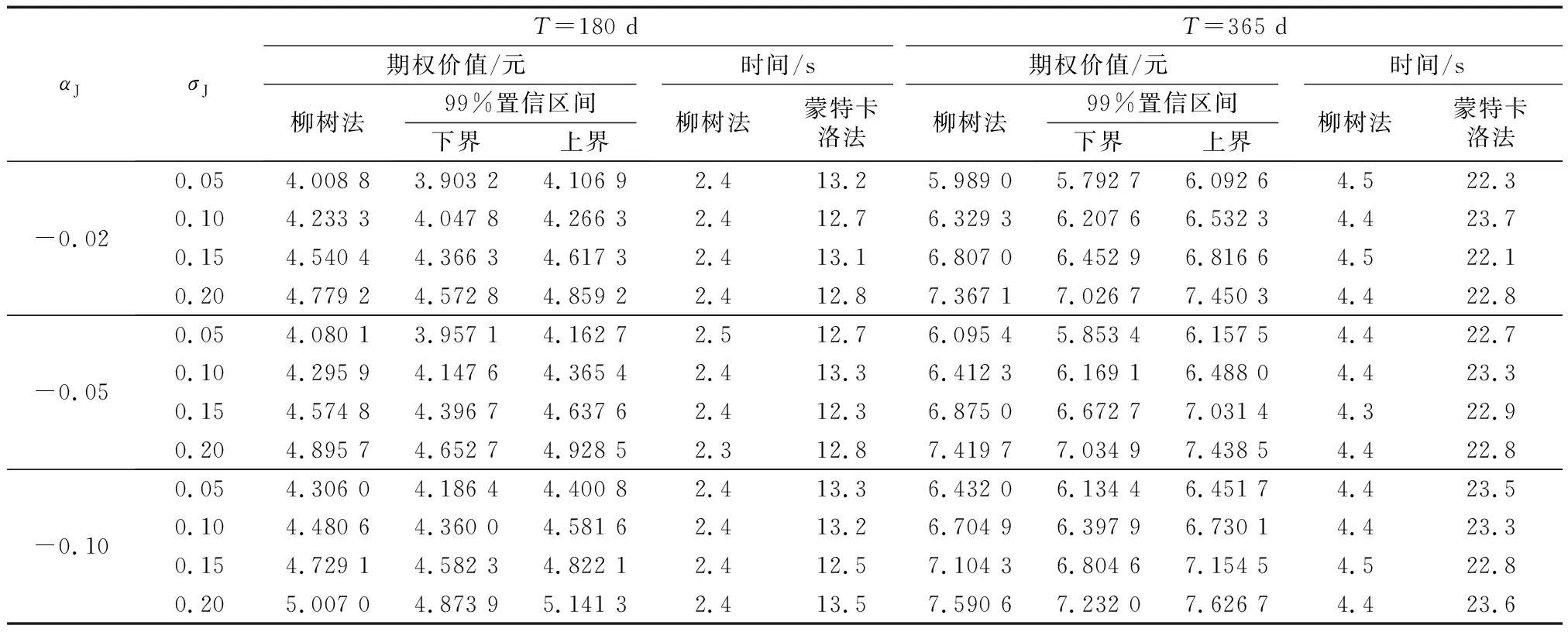
表4 不同到期日下，柳树法和蒙特卡洛法定价Merton跳扩散亚式期权的结果Tab.4 Results of willow tree method and Monte Carlo mothed at different T values

4 总结

亚式期权作为目前金融市场上较活跃的新型期权之一，由于其路径依赖关系，定价公式求解复杂，因此亚式期权的定价问题一直受到众多研究学者的关注.本文基于Merton的跳扩散模型，运用柳树法对亚式看涨期权进行了定价研究.首先，本文介绍了柳树的构造过程，主要分为两步：一是利用Johnson曲线转换公式的逆变换，通过计算随机变量的四阶矩，将一个标准正态分布的随机变量转换成一个服从跳扩散过程的连续随机变量，得到标的资产价格的估计；二是根据跳扩散模型满足的条件概率函数，推导出了相邻两个时间节点间的转移概率矩阵，计算得到相邻时刻间的转移概率.在亚式期权定价过程中，引入了插值技术解决平均价格路径较多的问题，仅存储了一定数量的平均价格节点，大大减少了计算时间，并给出了一种计算复杂度为O(N2)的柳树法.另外，本文还对该算法的截断误差和插值误差分别进行了误差分析，证明了柳树法的整体误差为O(Δt)+O(E[η5]).最后，本文用柳树法定价Merton跳扩散模型下亚式期权的结果与蒙特卡洛方法比较，数值实验的结果表明，柳树法不仅能达到蒙特卡洛方法的计算精度，而且在运行时间上明显少于蒙特卡洛方法，从而说明了柳树法在亚式期权定价中的优势.本文中研究的Merton跳扩散模型只是Levy过程中的一种，除此之外的Levy过程[15]还有Kou提出的双指数跳扩散模型，NIG模型和VG模型等，较之Merton跳扩散模型，这些过程的条件概率的密度函数不存在显示的表达式，将柳树法推广到这些模型，是我们未来的研究方向之一.