基于随机森林的出租车保有量预测方法研究
赵楠 姚宝珍

摘 要:为了使出租车合理分担一部分城市出行需求,兼顾运营效率和服务水平,本文提出了基于随机森林的出租车保有量预测模型。在文中考虑了城市人口、居民消费价格指数、平均等车时间、公交线路总长和网约车保有量等5个影响出租车保有量的相关因素。并且,通过内蒙古通辽市主城区实际数据对模型进行校验,并得到若干结论。
关键词:出租车保有量 随机森林 网约车 预测
一、引言
近年来,随着生活水平的提高和城市交通压力的增加,出租车需求快速增长。但是由于出租车规模和价格的限制,出租车需求供给矛盾突出。产生这种矛盾现象的主要诱因之一是出租车运力规模:运力规模过剩,虽然使乘客的平均等待时间减少,但出租车空载里程过高,司机的收入大幅下降;相反,运力规模不足,虽然出租车司机的收入有所增加,但乘客的等待时间过长,甚至降低出租车对整个城市交通的分担率。而“互联网+”和共享经济的兴起改变了传统的运输服务。自网约车合法化后,城市出租车运力得到了一定的补充,但是供需矛盾依然存在。因此,如何在出租车和网约车相互配合模式下,确定出租车的运力规模,是城市交通管理部门的重要课题。
国内外学者针对出租车规模和出租车运价问题做了很多研究。Beesley和Glaiste建模考察了出租车价格以及其服务弹性,同时研究了运力投放问题。研究结论表明,降低价格或者增加运力投放并不一定会降低利润。Yang等引入多个外生变量和内生变量,建立了乘客需求、出租车利用率和服务水平的联立方程模型,并以此获得有用的监管信息,合理做出关于出租车数量、收费结构、服务质量的决策。胡继华等通过城市出租车的GPS数据,挖掘出租车关于平均运营距离、平均运营时间、平均出行距离等运营信息,给出了一定需求和空载率下的确定出租车合理规模的方法,提出以小时为单位对出租车规模进行分时段控制。宋安和刘琦建立了出租车运力规模综合评价模型,并在此基础上提出基于供需平衡的预测方法,从而预测出租车运力规模。但该预测模型有一定的局限性,忽视了乘客等车时间等重要因素。杨英俊和赵祥模讨论了影响出租车保有量的相关因素,并通过小波神经网络对出租车保有量进行预测。Yang等基于GPS跟踪数据,构建了城市出租车运力规模计算模型。Belletti和Bayen针对Uber和Lyft这类公司,研究了基于响应需求的运力规模优化。
本文选取了城市人口、居民消费价格指数、平均等车时间、公交线路总长和网约车保有量等5个影响出租车保有量的相关因素,通过随机森林预测方法对出租车保有量进行预测。并以内蒙古通辽市主城区的相关数据为支撑,进行计算和分析。
二、基于随机森林的出租车保有量预测模型
(一)影响因素选择
在选择影响出租车保有量的因素时,应该遵循三个原则,即具有测量性、代表性和可比性。城市出租车系统主要受需求影响。随着社会经济的快速发展和城市规模的不断扩大,出租车需求日益提升,因此体现需求的相关因素尤为重要。另外,出租车作为城市公共交通的补充,其发展与城市公交系统建设密切相关,因而公交相关因素也对出租车规模有影响。综上考虑,本文将选取城市人口、居民消费价格指数、平均等车时间、公交线路总长和网约车保有量等5个因素作为出租车保有量的主要影響因素。
预测过程如下:首先将以上5个因素的相关数据和出租车保有量数据分为训练集和测试集,训练集用于训练随机森林模型,生成决策树;然后将测试集数据输入到训练好的随机森林模型中,进行预测;最后输出出租车保有量。
(二)随机森林算法
随机森林算法是基于Bagging的集成学习算法。该算法基于多棵决策树构建组合模型对样本进行分析预测。多数机器学习的方法倾向于在模型训练时,以经验风险最小化为原则求解最优模型,泛化能力差。但是随机森林可以避免过拟合问题。本文将采用随机森林对出租车保有量进行预测。下面将对随机森林算法进行简要说明(具体细节可以参考文献[7]-[8])。
For i=1 to N,N表示决策树的棵数:
1.从训练集P中基于Boostrap方法抽取M个样本;
2.从r属性中q个属性
3.选择最佳属性j和切分点s
4.建立决策树Ti
End
输出所有决策树集合 ,构成随机森林。
三、应用实例
(一)数据
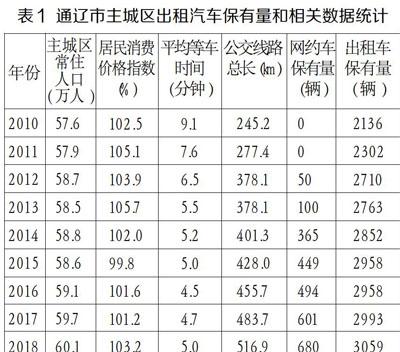
本文以内蒙古通辽市主城区的出租车保有量预测为例,对基于随机森林的出租车保有量预测模型进行验证和分析。通辽市位于内蒙古自治区的东部,总面积59535平方公里,城市道路网密度约2.32公里/平方公里,2018年地区生产总值1301.6亿元,截止2018年底全市总人口为313.3万人,其中通辽市主城区常住人口约为60万人,截止2018年底通辽市主城区出租车保有量为3059辆。通辽市主城区的2010-2018年数据如表1所示,包括了城市常住人口、居民消费价格指数、平均等车时间、公交线路总长、网约车保有量和出租车保有量相关数据。
在计算时,将数据按上半年和下半年进行了细分以增加样本数量。2010-2015年数据为训练集,用于随机森林训练。2016-2018年数据为测试集,用于检验随机森林预测精度。然后对本文中随机森林算法的参数进行说明,决策树的棵数N为50,总属性r为5,随机选择属性数量q为3。
(二)训练模型
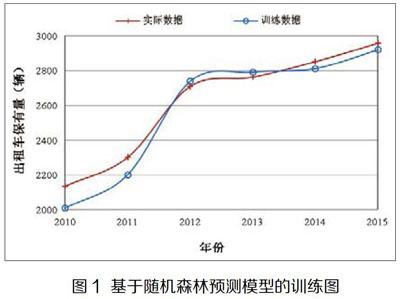
基于随机森林预测模型的出租车保有量训练曲线如图1所示。蓝线为实际数据,红线为训练数据,2010年到2011年预测数据小于实际数据,2012年到2013年预测数据大于实际数据,2014年到2015年预测数据小于实际数据。虽然出租车保有量数据有一定波动,但是训练数据可以很好地跟随实际数据,随着训练数据的增加,预测数量与实际数据的拟合度越来越高。通过计算可知,平均绝对误差百分比为2.52%,R方为0.94,这两个数据也侧面说明了随机森林的拟合优度。基于随机森林的出租车保有量预测模型具有较强的识别能力,随机森林通过平均决策树,可以降低过拟合问题出现的概率。同时,随机森林的拟合效果稳定,即使出现了新的数据点,也只是影响一棵决策树,不会对整体算法受到太大影响。
(三)预测模型
本文用训练好的预测模型和支持向量机模型对2016-2018年的出租车保有量进行预测,并将两种预测方法进行对比分析。两种算法的绝对误差百分比如图2所示。随机森林的平均绝对误差百分比0.34%,R方为0.93。支持向量机的平均绝对误差百分比0.64%,R方为0.77。可以看出,随机森林的预测表现要优于支持向量机。支持向量机的预测效果受其参数的影响,为了获得较好的结果,通常还需要对其参数进行优化。即使在本文中对参数进行优化后,支持向量机的预测误差仍大于随机森林的预测误差。从计算时间上看,支持向量机训练的过程较为费时,特别是在非线性核的情况下,计算时间显著增加。而且数据量增加后,差距也随之增加。所以和支持向量机相比,随机森林不仅可以获得较优的预测值,还可以节约计算的时间。
本文通过随机森林预测模型,对2020年通辽市主城区出租车保有量进行预测。首先要对2020年通辽市主城區的城市常住人口、居民消费价格指数、平均等车时间、公交线路总长、网约车保有量进行预测。然后将5个影响因素预测值输入到随机森林预测模型中,进行出租车保有量预测,预计2020年通辽市主城区的出租车保有量为3156辆。
四、结论
本文构建了基于随机森林的出租车保有量预测模型,在选择影响出租车保有量的因素时,主要考虑了需求、公共交通以及网约车等方面,选取城市常住人口、居民消费价格指数、平均等车时间、公交线路总长和网约车保有量等5个因素作为出租车保有量的主要影响因素。基于通辽市主城区数据,先对随机森林进行训练,然后用训练好的模型进行测试。结果表明本文提出的预测方法拟合程度较好且预测精度较高,可以避免过度拟合等问题。该方法可以对城市出租车保有量进行有效的预测,不仅降低管理成本,提高运营效率,增加社会效益,还可以为城市交通客运管理部门确定合理的出租车保有量及类似城市出租车管理都提供了良好的借鉴和参考价值。由于影响出租车保有量的因素比较多,其他城市在应用该预测方法时,可以根据城市的特点,选择相应的影响因素,以获得较好的预测结果。
有效预测出租车保有量还可以有效提高经济效益和社会效益,发挥出租车行业作为准公共交通的作用:
(一)较为准确地预测出租车保有量能够提前对运输资源进行高效合理分配,方便群众出行,提高服务质量,平衡供给和需求,有利于提高运营者的经济效益,同时也降低了出行者的等待时间,实现社会福利的提升。
(二)随着生活水平的提高,居民对出租车的运力需求随之增加。出租车和网约车形成了相互配合的良好运营关系,为城市出行增加运力,扩大社会就业,有效帮扶困难群体,促进就业和经济双增长。
(三)出租车是城市精神文明的一个流动服务窗口,其运营秩序的好坏、服务质量的优劣,体现了一个城市的管理水平和文明程度,直接关系到城市的声誉和整体形象,甚至代表着当地政府的形象和市民的整体素质。城市出租车保有量的确定在树立城市形象等方面发挥着重要作用。
(四)随着城乡一体化进程的推进,城乡公共服务一体化也逐步布局,均衡配置城乡公共运力资源有利于促进城乡要素平等交换和公共资源合理安排,从而带动城乡经济发展。做好地区出租汽车客运的发展规划和总量控制,可以防止盲目发展无序竞争,确保道路旅客运输市场健康发展和社会稳定。
参考文献:
[1] Beesley, M. E., Glaister, S. Information for regulation: the case of taxi[J]. The Economic Journal, 1983, 93.
[2] Yang, H., Lau, Y. W., Wong, S. C., Lo, H. K. A macroscopic taxi model for passenger demand, taxi utilization and level of services[J]. Transportation, 2000, 27(3).
[3] 胡继华, 谢海莹. 基于浮动车数据的出租车规模确定方法[J]. 交通标准化, 2011,(18).
[4] 宋安, 刘琦. 出租车保有量评价与预测[J]. 交通科学与经济, 2010, (3).
[5] 杨英俊, 赵祥模. 基于小波神经网络的出租车保有量预测模型[J]. 公路交通科技, 2012, 8(29).
[6] Yang, Y., Yuan, Z., Fu, X., Wang, Y., Sun, D. Optimization Model of Taxi Fleet Size Based on GPS Tracking Data[J]. Sustainability, 2019, 11(3).
[7] Belletti, F., Bayen, A. M. Privacy-preserving MaaS fleet management[J]. Transportation Research Part C: Emerging Technologies, 2018,(94).
[8] Liaw, A., Wiener, M. Classification and regression by random Forest. R news, 2002, 2(3).
[9] Pal, M. Random forest classifier for remote sensing classification. International Journal of Remote Sensing, 2005, 26(1).
(作者单位:1.通辽市交通科学研究所;2.大连理工大学)

