两个含Smarandache LCM函数的复合数论函数方程的可解性
张明丽,高 丽,申江红
(延安大学数学与计算机科学学院,陕西延安716000)
上世纪90年代,美国著名的数学家F.Smarandache[1]提出了许多新的数论问题,并定义了若干新的数论函数,对现代数论的发展产生了较大的影响。其中以F.Smarandache本人命名的Smarandache函数S(n),以及在其基础上衍生出的若干数论函数,如Smarandache LCM函数SL(n),近年来受到国内外诸多学者的广泛关注和深入研究。对于任意的正整数n,Euler函数φ(n)定义为在序列1,2,…,n-1中与n互素的整数的个数,Euler函数是数论中一个重要的积性函数。Smarandache函数S(n)表示为,对于任意的正整数n,S(n)=min{m∈Z:n|m!}。Smarandache LCM函数SL(n)表示为,对于任意的正整数n,若n=p1r1p2r2…pkrk,其中所列的p1,p2,…,pk均为素数且顺序排列,则Smarandache LCM函数SL(n)=max{p1r1,p2r2,…,pkrk}。近年来,关于上述数论函数方程相互结合求解及性质的研究备受关注。张天平[2]研究了复合欧拉函数方程φ(φ(n))=2Ω(n)的奇数解;田呈亮[3]研究了复合欧拉函数方程φ(φ(n))=2Ω(n)的正整数解;多布杰[4]研究了复合欧拉函数方程φ(φ(n))=2t的可解性问题。
近期,王洋、张四保[5]研究了复合欧拉函数方程φ(φ(n-φ(φ(n))))=2的可解性问题,但求解过程较为繁琐,故袁合才、王波等[6]对其求解方法加以简化,研究了复合欧拉函数方程φ(φ(n-φ(φ(n))))=4,6的可解性问题。张利霞、赵西卿等在文献[7-8]中分别研究了数论方程S(SL(n))=φ(n),
S(SL(n))=φ2(n)的可解性,郭梦媛、高丽等在文献[9]研究了S(SL(n2))=φ2(n)的可解性。本文基于此,探究了含Smarandache LCM函数的复合数论函数方程φ(φ(n-S(SL(n))))=8,10的可解性问题。
1 相关引理

引理2[7]当n≥2时,有φ(n) 引理3[7]对于整数k和素数p,有S(Pk)≤kp;当且仅当k 证明由引理1—引理3易知,当满足条件时, l=n-S(SL(n))≥n-kp≥ 则有l+1≤n≤2l,证毕。 定理1 含Smarandache LCM函数的复合数论函数方程 φ(φ(n-S(SL(n))))=8 (1) 的正整数解为n=34,51,50,30,44,55,72,77,42,49,45,52,54,56,65,64,81,91,90,98,100,62,93。 证明因为φ(φ(n-S(SL(n))))=8,所以 φ(n-S(SL(n)))=15,16,20,24,30。下面分5种情况加以讨论: 情形一:若φ(n-S(SL(n)))=15,由引理2可知式(1)无解。 情形二:若φ(n-S(SL(n)))=16,则 n-S(SL(n))=17,32,34,40,48,60。 当n-S(SL(n))=17时,由引理4,此时18≤n≤34,将其逐一代入验证,只有n=34满足 n-S(SL(n))=17,即n=34为式(1)的解。 当n-S(SL(n))=32时,由引理4,此时33≤n≤64,将其逐一代入验证,此时式(1)无解。 当n-S(SL(n))=34时,由引理4,此时35≤n≤68,将其逐一代入验证,只有n=51满足 n-S(SL(n))=34,即n=51为式(1)的解。 当n-S(SL(n))=40时,由引理4,此时41≤n≤80,将其逐一代入验证,只有n=50满足 n-S(SL(n))=40,即n=50为式(1)的解。 当n-S(SL(n))=48时,由引理4,此时49≤n≤96,将其逐一代入验证,此时式(1)无解。 当n-S(SL(n))=60时,由引理4,此时61≤n≤120,将其逐一代入验证,此时式(1)无解。 情形三:若φ(n-S(SL(n)))=20,则 n-S(SL(n))=25,33,44,50,66。 当n-S(SL(n))=25时,由引理4,此时26≤n≤50,将其逐一代入验证,只有n=30满足 n-S(SL(n))=25,即n=30为式(1)的解。 当n-S(SL(n))=33时,由引理4,此时34≤n≤66,将其逐一代入验证,只有n=44满足 n-S(SL(n))=33,即n=44为式(1)的解。 当n-S(SL(n))=44时,由引理4,此时45≤n≤88,将其逐一代入验证,只有n=55满足 n-S(SL(n))=44,即n=55为式(1)的解。 当n-S(SL(n))=50时,由引理4,此时51≤n≤100,将其逐一代入验证,此时式(1)无解。 当n-S(SL(n))=66时,由引理4,此时67≤n≤132,将其逐一代入验证,只有n=72,77满足 n-S(SL(n))=66,即n=72,77为式(1)的解。 情形四:若φ(n-S(SL(n)))=24,则 n-S(SL(n))=35,39,45,52,56,70,72,78,84,90。 当n-S(SL(n))=35时,由引理4,此时36≤n≤70,将其逐一代入验证,只有n=42,49满足 n-S(SL(n))=35,即n=42,49为式(1)的解。 当n-S(SL(n))=39时,由引理4,此时40≤n≤78,将其逐一代入验证,只有n=45,52满足 n-S(SL(n))=39,即n=45,52为式(1)的解。 当n-S(SL(n))=45时,由引理4,此时46≤n≤90,将其逐一代入验证,只有n=54满足 n-S(SL(n))=45,即n=54为式(1)的解。 当n-S(SL(n))=52时,由引理4,此时53≤n≤104,将其逐一代入验证,只有n=56,65满足n-S(SL(n))=52,即n=56,65为式(1)的解。 当n-S(SL(n))=56时,由引理4,此时57≤n≤112,将其逐一代入验证,只有n=64满足 n-S(SL(n))=56,即n=64为式(1)的解。 当n-S(SL(n))=70时,由引理4,此时71≤n≤140,将其逐一代入验证,此时式(1)无解。 当n-S(SL(n))=72时,由引理4,此时73≤n≤144,将其逐一代入验证,只有n=81满足 n-S(SL(n))=72,即n=81为式(1)的解。 当n-S(SL(n))=78时,由引理4,此时79≤n≤156,将其逐一代入验证,只有n=91满足 n-S(SL(n))=78,即n=91为式(1)的解。 当n-S(SL(n))=84时,由引理4,此时85≤n≤168,将其逐一代入验证,只有n=90,98满足 n-S(SL(n))=84,即n=90,98为式(1)的解。 当n-S(SL(n))=90时,由引理4,此时91≤n≤180,将其逐一代入验证,只有n=100满足 n-S(SL(n))=90,即n=100为式(1)的解。 情形五:若φ(n-S(SL(n)))=30,则 n-S(SL(n))=31,62。 当n-S(SL(n))=31时,由引理4,此时32≤n≤62,将其逐一代入验证,只有n=62满足 n-S(SL(n))=31,即n=62为式(1)的解。 当n-S(SL(n))=62时,由引理4,此时63≤n≤124,将其逐一代入验证,只有n=93满足 n-S(SL(n))=62,即n=93为式(1)的解。 定理2 含Smarandache LCM函数的复合数论函数方程 φ(φ(n-S(SL(n))))=10 (2) 的正整数解为n=46,69。 证明因为φ(φ(n-S(SL(n))))=10,所以 φ(n-S(SL(n)))=11,22。下面分2种情况加以讨论: 情形一:若φ(n-S(SL(n)))=11,由引理2可知式(2)无解。 情形二:若φ(n-S(SL(n)))=22,则 n-S(SL(n))=23,46。 当n-S(SL(n))=23时,由引理4,此时24≤n≤46,将其逐一代入验证,只有n=46满足 n-S(SL(n))=23,即n=46为式(2)的解。 当n-S(SL(n))=46时,由引理4,此时47≤n≤92,将其逐一代入验证,只有n=69满足 n-S(SL(n))=46,即n=69为式(2)的解。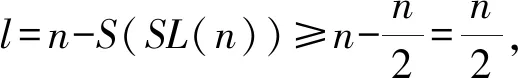
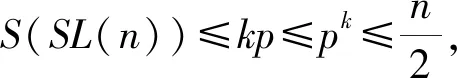
2 主要结论及其证明

