Isomorphic embeddings of Banach spaces

ZHENG Bentuo

（Department of Mathematical Sciences，The University of Memphis，TN 38152-3240，USA）

Abstract： This paper reviewed the studies on isomorphic embeddings of Banach spaces into superspaces with Schauder bases，shrinking bases，boundedly bases，unconditional bases and spreading bases.Major problems and related achievements are presented in the hope that such a survey would be helpful to researches on this topic.

Key words： isomorphic embedding；weakly null trees；unconditional bases；spreading bases

One of the fundamental tasks of Banach space theory is to determine whether a given Banach space can be embedded isomorphically into another Banach space.To be more precise，given two Banach spaces X and Y，does there exist a linear homeomorphism T from X into Y? If T is a linear isometry，we say that X embeds isometrically into Y.One reason of investigating the problem is that if we can embed a space X with very “bad” structure into a space Y with very “nice” structure，then we may use the structure of Y to study the properties of X.Banach spaces with Schauder bases are considered to be spaces with “nice” structure.P.Enflo[1]discovered in 1973 that there are Banach spaces which fail the approximation property and hence fail to have Schauder bases.Recall that a Banach space X is said to have a Schauder basis if there exist a sequence of vectorsin X so that each element x in X has a unique representationwhere （ai） is a sequence of scalars so that the infinite sum converges in norm.It can be shown that there are a sequence of functionalsin the dual space X*of X so thatfor all i，j∈N.In this caseis called the biorthogonal functionals ofFrom the discussion above，the following question becomes very natural.

Question 1Let X a separable Banach space.Does X embed isomorphically into a Banach space with a basis?

Theorem 1（Banach-Mazur）Every separable Banach space X embeds isometrically into C[0，1]，where C[0，1]is the space of continuous functions on the unit interval with the sup norm.

Since C[0，1]has Schauder basis，the famous Banach-Mazur theorem gives an affirmative answer to Question 1.In certain situations，we may be able to embed a Banach space isomorphically into another space with a“good” Schauder basis.A Schauder basisof a Banach space X is called shrinking if the biorthogonal functionalsform a Schauder basis for X*.A Schauder basisis called boundedly complete if，for every sequence of scalarssuch that，the seriesconverges.It is well known that a Banach space X with a boundedly complete Schauder basisis isomorphic to a dual space.More precisely，X is isomorphic to the dual of the subspace spanned by the biorthogonal functionalsof X*.A Banach space X with a Schauder basisis reflexive if and only ifis both shrinking and boundedly complete.If the dual space X*has a Schauder basis，then X has a shrinking Schauder basis and X*has a boundedly complete Schauder basis.

Question 2When does a separable Banach space embed isomorphically into a Banach space with a shrinking Schauder basis?

It is easy to see that if a Banach space X embeds isomorphically into a Banach space with a shrinking Schauder basis，then the dual space X*is separable.In 1988，M.Zippin[2]proved that the converse is also true.

Theorem 2[2]Every Banach space with a separable dual embeds isomorphically into a Banach space with a shrinking Schauder basis.

It should be pointed out that the dualization of the theorem of Zippin was proved earlier by W.J.Davis，T.Figiel，W.B.Johnson and A.Pelczynski[3]in 1974.

Theorem 3[3]If X*is separable，then X*embeds isomorphically into a Banach space with a boundedly complete Schauder basis.

As a corollary，the following result was shown in the same paper of Zippin.

Theorem 4[2]Every separable reflexive Banach space embeds isomorphically into a reflexive Banach space with a Schauder basis.

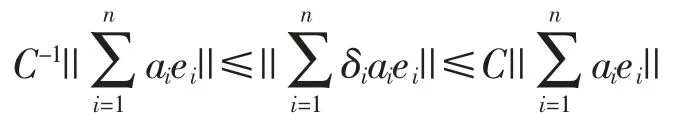
Question 3When does a separable Banach space embed isomorphically into a Banach space with an unconditional basis?

Before we give an answer to Question 3，we need to introduce the following notions.Let X be a Banach space.SXdenotes the unit sphere of X.Let [N]<ωdenote all finite subsets of the positive integers.By a normalized weakly null tree，we mean a family（xA）A∈[N]<ω⊂SXwith the property that every sequence （xA∪{n}）n∈Nis weakly null.Let A={n1，…，nm} with n1<…0.X has the UTP if X has the C-UTP for some C≥1.In 2008，W.B.Johnson and the author[4]gives an answer to Question 3 for reflexive spaces.

Theorem 5[4]Let X be a separable reflexive space with the UTP.Then X embeds isomorphically into a reexive Banach space with an unconditional basis.

It is not hard to see that any subspace of a reflexive Banach space with an unconditional basis has the UTP.With more efforts，W.B.Johnson and the author[5]answers Question 3 for Banach spaces with separable duals in2011.A normalized weak*null tree in X*is a family （xA*）A∈[N]<ω⊂SX*with the property that every sequenc（xA∪{n}）n∈Nis weak*null.A Banach space X is said to have the w*-UTP if every normalized weak*null tree in X*admits a branch which is an unconditional basic sequence.If X is reflexive，then the w*-UTP is （obviously） equivalent to X*having the UTP.

Theorem 6[4]Let X be a Banach space so that X*is separable.If X has the w*-UTP，then X embeds isomorphically into a Banach space with a shrinking unconditional basis.

The following question is still open.

Question 4Let X be a separable Banach space so that X*is nonseparable.When does X embed isomorphically into a Banach space with an unconditional basis?

A special and crucial case is to determine when a given Banach space embeds isomorphically into l1.

Question 5Let X be a separable Banach space.When does X embed isomorphically into l1?

Theorem 7[6]Let X be a Banach space with separable dual.If every normalized weakly null tree in X admits a branch which is equivalent to the unit vector basis of c0，then X embeds isomorphically into c0.

Theorem 8[7]Let X be a separable reflexive Banach space and let 1

Question 6Let X be a separable Banach space.When does X embed isomorphically into a Banach space with a spreading basis?

Since every Banach space with an unconditional basis embeds isomorphically into a Banach space with a symmetric basis.By the aforementioned result of W.B.Johnson and the author，every Banach space with separable dual and w*-UTP embeds isomorphically into a Banach space with a symmetric basis.This solves a special case of Question 6.So we have the following open problem.

Question 7Let X be a separable Banach space.When does X embed isomorphically into a Banach space with a conditional spreading basis （spreading basis which is not unconditional）?

Final remarkIn this short survey on isomorphic embeddings of Banach spaces into superspaces with Schauder bases，shrinking bases，boundedly bases，unconditional bases and spreading bases，we collect and discuss some important open problems.Achievements and progresses on solving these problems are introduced as well.All questions listed here are of great significance and worth further investigation.