弱非完整系统的积分因子与守恒律

陈 杰， 张 毅

（苏州科技大学 土木工程学院，江苏 苏州 215011）

当力学系统的运动微分方程难以求解时，若能找到系统的某个守恒量，将会使人们对该系统的性质有所了解。寻找守恒律的近代方法主要基于系统的对称性：Noether 对称性[1]、Lie 对称性[2]、Mei 对称性[3]等。1984年，Djuki提出了寻求非保守动力学系统守恒量的积分因子方法[4]，即通过运动微分方程乘以适当的积分因子直接构造系统的守恒律。乔永芬[5-7]、张毅[8-11]将积分因子方法进行了一系列的推广。但是，对于弱非完整系统的守恒律的研究还主要限于Noether 对称性[12]、Mei 对称性[13]、Lagrange 对称性[14]等。笔者将积分因子方法应用于弱非完整系统中，利用幂级数展开[15]，求得弱非完整系统的近似守恒量。该方法限制条件少且易于计算，因此，具有广泛的应用价值。

1 弱非完整系统的积分因子

假设力学系统的位形由n 个广义坐标qs（s=1，2，…，n）确定，系统的运动受有g 个理想双面线性弱非完整约束

其中μ 是小参数。当μ≠0 时，系统是弱非完整的；当μ=0 时，系统成为完整的。系统的运动微分方程可以表示为

要注意的是，小参数μ 只出现在非完整约束反力∧s中。

为了更好地便于计算和了解弱非完整系统的动力学特征，可以将对于小参数μ 进行幂级数展开[15]，可得

一次近似为

二次近似为

高次近似为

方程（5）-（7）分别称为弱非完整系统（3）相应的一次近似系统、二次近似系统与高次近似系统的运动微分方程。

零次近似系统与参数μ 无关，可参考文献[9]给出的积分因子及其守恒定理。

下面研究一次近似系统、二次近似系统与高次近似系统的运动微分方程，即方程（5）-（7）。

定义1如果函数ξs＝ξs（t，q，）满足以下条件，对于一次近似系统，有

对于二次近似系统，有

对于高次近似系统，有

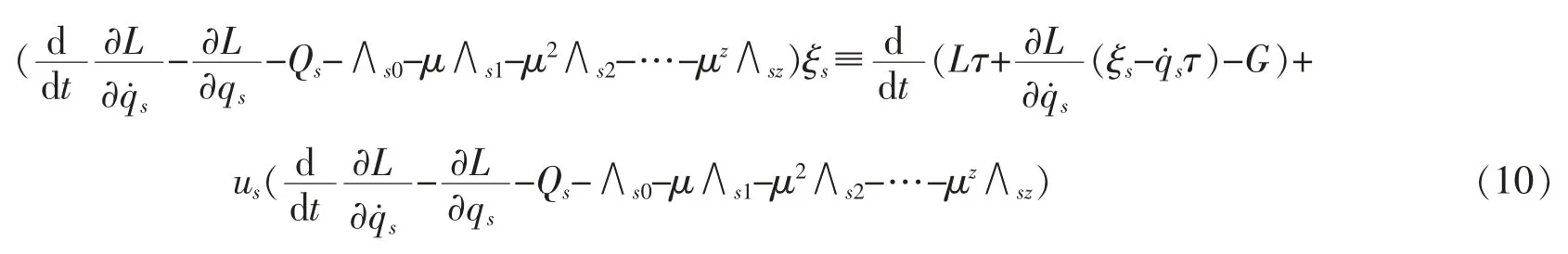
其中τ，G 和us为t，q，的函数，则称函数ξs＝ξs（t，q，）分别为弱非完整系统（3）的一次近似系统、二次近似系统与高次近似系统的积分因子。

2 弱非完整系统的守恒定理

联合式（5）与式（8），式（6）与式（9），式（7）与式（10）分别可得

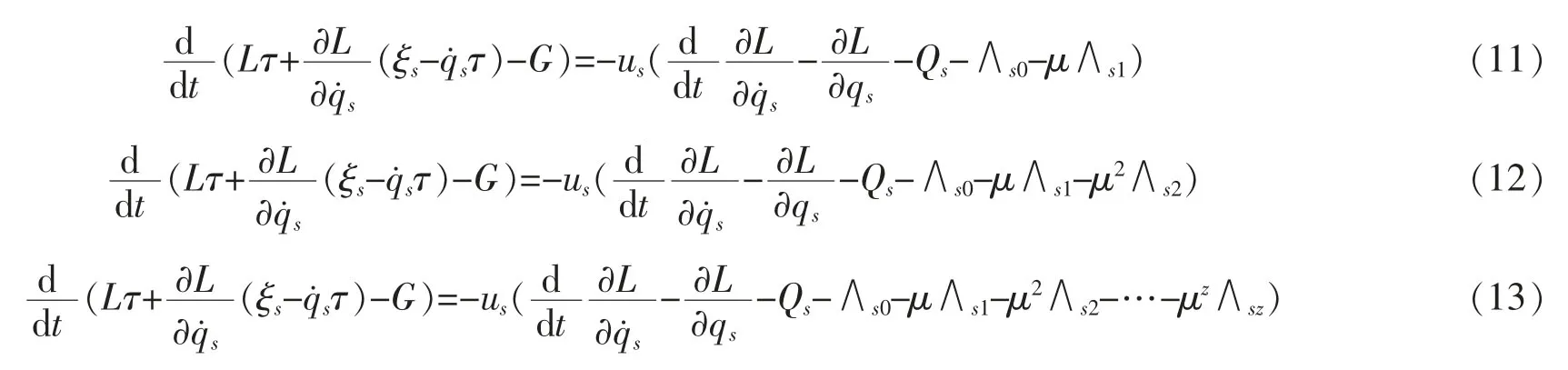
定理1如果函数ξs是弱非完整系统（3）的一次近似系统、二次近似系统与高次近似系统的积分因子，那么弱非完整系统（3）存在如下守恒量

对于弱非完整系统（3），如果函数ξs是其一次近似系统的积分因子，则每一组函数ξs、τ、G 和us必须满足必要条件（11）。如果函数ξs是其二次近似系统的积分因子，则每一组函数ξs、τ、G 和us必须满足必要条件（12）。如果函数ξs是其高次近似系统的积分因子，则每一组函数ξs、τ、G 和us必须满足必要条件（13）。条件（11）-（13）分别可以写成

如果满足必要条件（15）、（16）或（17）的函数组ξs、τ、G 和us使得（14）式右端的值为一个特定常数，则称该函数组为奇异的。因此，有以下定理：

定理2对于每个非奇异函数组ξs、τ、G 和us，如果满足必要条件（15）、（16）或（17），那么弱非完整系统（3）存在近似守恒量（14）。

对于满足必要条件（15）、（16）或（17）的任意非奇异函数组ξs、τ、G 和us，都可以找到该系统的一个守恒律。为了找出函数组ξs、τ、G 和us，可以将方程（15）、（16）或（17）展开，并分别令含的项和不含的项的系数为零，得到

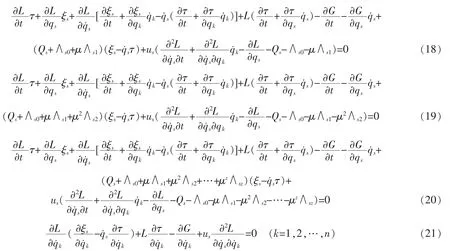
其中，式（18）与（21）、式（19）与（21）或式（20）与（21）是关于（2n+2）个未知函数ξs、τ、G 和us的（n+1）个偏微分方程，可以称为广义Killing 方程。由于未知数的数目是大于方程数，所以该广义Killing 方程的解不是唯一的，可以找出不同的合适的ξs、τ、G 和us的值，从而得到系统不同的守恒量。

3 守恒定理的逆定理

假设弱非完整约束系统（3）有积分

显然该积分对应的积分因子ξs和函数τ、G、us必须与必要条件（15）-（17）相容。由方程（14）得出并代入式（21），有

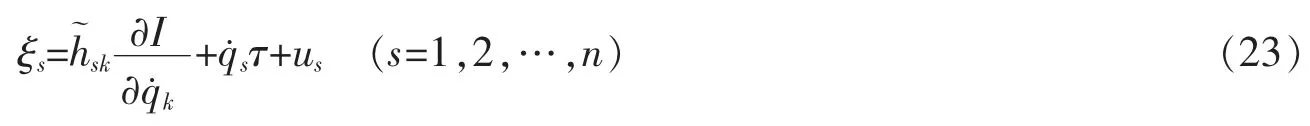
从式（24）得

因此，可以得出以下定理：

定理3如果弱非完整系统（3）有一个第一积分（22），则与此积分相对应的积分因子ξs和函数τ、G、us由关系式（23）和（25）确定。

方程（23）与（25）是关于（2n+2）个函数的（n+1）个代数方程，故函数ξs、τ、G、us并不是唯一的。对于同一个守恒量，通过解方程（23）与（25），可以求出不同的积分因子ξs。

4 算例

例1系统的位形由两个广义坐标q1，q2来确定，系统的动能和势能分别为

系统的运动受到弱非完整约束

其中，μ 为小参数。试用积分因子方法研究系统的守恒量。

由方程（2）得

由方程（26）与（27）解出

根据方程（4）与（29）可以得出

对μ 进行幂级数展开，得

下面求该弱非完整系统相应的一次近似系统的积分因子与守恒律。

由广义Killing 方程（18）与（21）可得

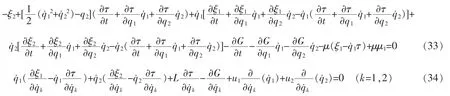
由方程（33）与（34）可得出一组解

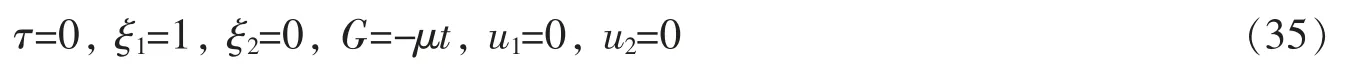
根据式（14）可得系统的守恒量

再根据逆定理，假设系统有积分

由方程（23）与（25）可得

上述3个方程有6个未知量，所以解不唯一，可以取

则有

下面求该弱非完整系统相应的二次近似系统的积分因子与守恒律。

由广义Killing 方程（19）与（21）可得

由方程（42）与（43）可得出一组解

根据式（14）可得系统的守恒量

再根据逆定理，假设系统有积分

由方程（23）与（25）可得

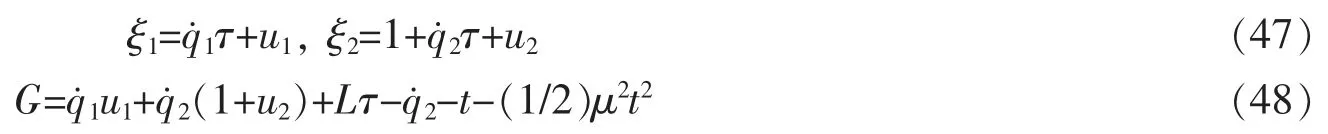
上述3个方程有6个未知量，所以解不唯一，可以取

则有

下面求该弱非完整系统相应的高次近似系统的积分因子与守恒律。

由广义Killing 方程（20）与（21）可得

由方程（51）与（52）可得出解

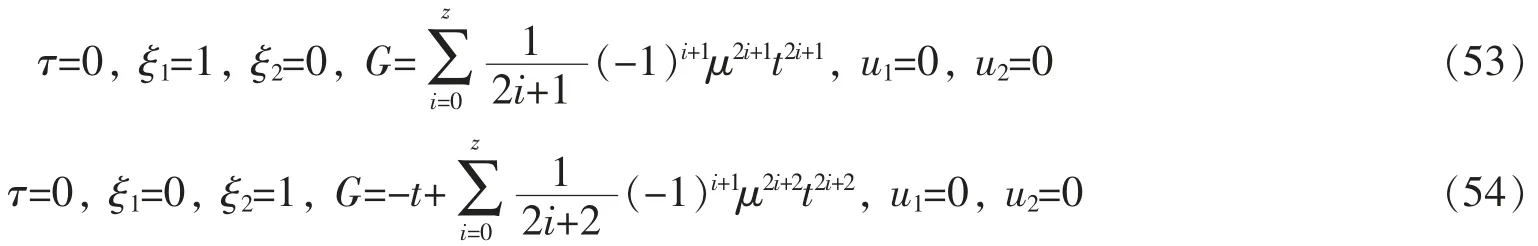
根据式（14）可得系统的守恒量

再根据逆定理，假设系统有积分

由方程（23）与（25）可得

上述3个方程有6个未知量，所以解不唯一，可以取

则有

或者取

则有

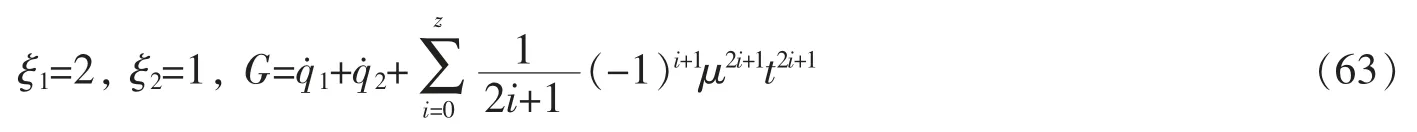
5 结语

积分因子方法由于其限制条件少且容易运算，因此，在求解约束力学系统的守恒律问题中得到了广泛应用。文章将积分因子方法推广应用于弱非完整系统，为求弱非完整系统的守恒律提供了一种新的方法。当弱非完整系统的小参数μ＝0 时，该结论适用于一般完整系统。当弱非完整系统的小参数μ＝1 时，该结论适用于一般非完整系统。因此，文中的结果具有普遍意义。