一道彰显直观想象试题的命制与分析

刘兴梓

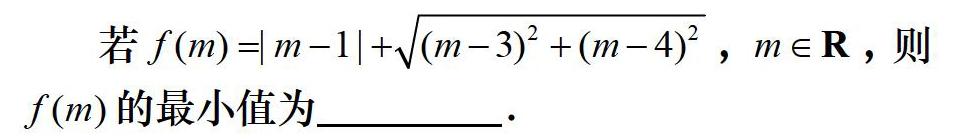
试题命制素材提倡源于生活中的问题，最终为生活服务.我们在试题命制探究过程中，应该学会挖掘生活素材，注意直观想象、数学抽象、逻辑推理、数学建模等学科核心素养之间密切关联.笔者结合一道试题命制与分析，与大家共享命制心路.

1 题目呈现f（m）的最小值为____.

2 考查目标

这是一道函数最值问题，试题简洁朴实，内涵深刻.本题以初等型函数为载体，以探寻函数最小值为目标.主要考查线段和差最值、点到直线垂线段最短、直线方程的倾斜角、解直角三角形、两点间距离公式、等腰三角形等知识;运用函数方程思想，化归与转化思想、数形结合等数学思想，考查学生的转化意识、数学语言互译能力及发现问题、分析问题、解决问题的能力.

3 命制过程

3.1 灵感来源

笔者翻阅数学与物理文化书籍，一则古老的数学问题引起了笔者的注意.

来源1 古老的胡不归问题

有一则历史故事说的是，一个身在他乡的小伙子得知父亲病危的消息后，便日夜赶路回家，然而他选择回家路线不当，最终当他气喘吁吁地来到父亲面前时，老人才刚刚咽气了.人们告诉他，老人在弥留之际，还在不断喃喃的叨念：“胡不归？胡不归？……”

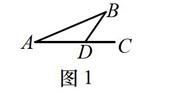
早期的科学家曾为这则古老的传说中的小伙子设想了一条路线（如图1）.A是出发地，B是目的地，AC是一条驿道，而驿道靠目的地的一侧全是砂土地带.为了急切回家，小伙子选择了直线路程AB.

他忽略了在驿道上行走要比在砂土地带行走快的这一因素.如果他能选择一条合适的路线（尽管这条路线长一些，但是速度可以加快），是可以提前抵达家门的.

那么这应该是哪条路线呢？显然，根据两种路面的状况和在其上面行走的速度值，可以在AC上选定一点D，小伙子从A走到D，然后从D折往B，可望最早到达B.用现代的科学语言表达就是：“己知在驿道和砂地上行走的速度分别为V1和V2，在AC上求一个定点D，使得A→D→B的行走时间最短.”

来源2 一道曾获得省级学科命题奖励的自创题

笔者于2014年参加福建省九科高考命题活动，以古老的胡不归问题为设计模式，题目设计如下：

如图2，已知甲在岸上4点处发现乙在B点处落水呼救，点B离岸上AC距离BC=30米，∠BAC=15°.甲在岸上跑步速度是水中游泳速度的√2倍，甲在水中游泳速度为3米/秒，设甲从A点到B点的时间为f秒，则f的最小值为____

.

解析 如图2，作∠CAD= 45°，记甲在岸上P点处入水，过点P作PH上AD于点H，此时，AP=√2.PH.又由于甲在岸上跑步的速度是水中游泳速度的√2倍，于是甲在岸上A所花时间等价于PH在水中所花时间，即甲从A点到B点的时间为PH+PB在水中游所花时间.过点B作BE⊥AD于点E，由点到直线垂线段最短可知PH+ PB≥BE，当且仅当B，P，日三点共线且点E与点H重合时等号成立.

题目以实际生活产生的研究性问题为背景，关键解决方案设计中的最优解.本题通过甲在岸上跑步速度与水中游泳速度之比，运用构造法把岸上的路程转化为水中的路程，再利用点到直线垂线段最短对线段之和的最小值求解，找到甲的入水点，从而提出最优方案.本题思维灵活，若用其他方法也可求解，但运算量较大.题目设计接近生活，符合高考对数学应用方面的考查要求.

来源3 教材习题

人民教育出版社普通高中课程标准实验教科书A版必修2第110页B组第8题：己知O

本题注重代数语言与几何语言互译，注重问题本质探索.解题若从代数单方面出发，解题难度明显较大.若从代数中蕴含的几何本质，则问题可迎刃而解.教材编者意图，以题目引导学生注重几何直观的重要性，以题目引领数形结合思想教学.

3.2 命制设想

设想1针对“灵感来源1”寻求古老的胡不归问题数学模型，揭示数学模型性质，看是否能用适当的函数来表示出来;

设想2在“灵感来源2”中，胡不归问题可创编具有生活意义的数学应用命题，这类数学文化题更贴近生活实际.从不同的高考命题角度看，此类型题能否再次设计成更加简洁易懂的数学问题;

设想3通过“灵感来源3”，可以初步认识在胡不归问题中，搭起“数”与“形”的桥梁为两点间的距离公式，命题设计可以从这一方面出发.

3.3 改进与定稿

鉴于以上“形”用“数”来表示，笔者决定用初等型函数形式体现问题，经过初步探讨，笔者命制初稿. 初稿若

说明题目直接以两点间距离的形式体现函数，对于学生而言，不难找出可用两点距离公式来转化成解析几何的形式，初稿后笔者发现，其一，题目暗含的运用“形”转化“数”太过明显;其二，对于线段题建模是有误差的.

第2稿若

说明经过不断思索，笔者降低题目难度并让模型靠近胡不归问题模型，使之达到命题有效性，解足问题，“2”改为“1”，使得点（m，m）与点（1，1）在直线y=x上，这时模型建立符合胡不归问题了.虽然

的设定不是很满意，于是决定在不改变问题背景和函数基本形态的情况下增加函数类型的复杂程度.

m∈R，则f（m）的最小值为____.

说明题目修改了函数的表示，部分以绝对值形式出现，这时题目函数的味道更浓，题目更加简洁了，对学生而言解题难度也有所提升.

4 解题思路

4.1 试题条件及目标

题目阅读量较少，条件有二，其一是：函数f（m）辅助说明条件一.从试题条件一分析，此函数类型包含绝对值函数和根式函数，不是高中常见初等函数类型.

试题目标为求f（m）的最小值.函数最值问题是高考命题、高中数学竞赛命题、高校自主招生命题常见题型，解决此类问题经常用到定义法、函数单调性法、导数法、换元法、配方法、不等式法、数形结合法等解题方法.

4.2 试题联想

联想1 |m-l|表示在数轴上点m到点1的距离;中点（m，m）到点（3，4）的距离.

由这两个联想结合函数类型，本题解题可以从“数”转化“形”入手.

4.3 试题拱桥

从以上两个联想出发，还是无法得到两个联想之间有何联系，这时需要适当转化，搭出|m-l|與成在平面直角坐标系表示为

此时问题这可转化为点（m，m）与（1，1）、（3，4）的关系.

当A，C，D三点共线且CD上直线y=l时，|AD|+|AC|取最小值，即f（m）取最小值为3，此时，点A的坐标为A（3，3）.

6 从学科素养角度评价试题命制

6.1 对直观想象素养的考查

直观想象为高中数学学科核心素养之一，从以胡不归问题模型的命题设计中，我们认识到函数本身体现自然规律，数皆可化为形，解答若借助直观想象，感知事物的形态，就可巧构形与数的关系解决数学问题.可见直观解决问题教学这种重要手段，是探索和形成论证思路的思维根本.通过直观想象构造论证求解，揭示函数本质，体现思维自然规律.

6.2 对数学建模素养的考查

此命题设计可让学生感受到数学文化问题初步模型的探索过程，对学生数学建模素养培养是有益的.数学建模渗入命题及教学过程中，让学生能够累积用数学建模解决疑难问题的宝贵经验，提升自身应用能力，增强自身创新品质.胡不归问题也是物理问题，跨学科设计题目，注重学科之间知识与技能关联，有利于培养学生运用模型解决问题能力.

参考文献

[1]裴光亚.数学是过程[J].中学数学，2002（8）：22-24

[2]陈敏，吴宝莹，数学核心素养的培养从教学过程的维度[J].课程改革，2015（4）：37-38