单分位数方法对时间序列尾指数变点检测及应用
周江娥 胡尧 商明菊




摘 要:多元时间序列中的尾指数变点检测在理论和实际应用中都有着广泛应用。本文利用单分位数方法(Single Quantile Method)构造检验统计量检测和估计出多元时间序列数据尾指数变点,证明其极限分布。在模拟研究中,分别产生三个经典的厚尾分布类型随机数进行模拟研究,结果表明,单分位数方法对多元时间序列尾指数的变点检测是有效的,尤其对分布变化造成的尾指数变化的情形更加敏感与准确。最后将该方法应用于深圳市香蜜湖路市委党校南行路段车流量数据,结果显示该方法能准确检测出交通流变点,根据存在的变点分析出交通流的变化规律。
关键词:单分位数方法; 变点; 多元时间序列; 厚尾分布; 尾指数
中图分类号:O212
文献标识码: A
通常,我们将样本用一个分布或者模型进行刻画,变点则是指其分布、模型或其参数突然发生改变之点称为变点,通过变点检测可以分析出造成该变点的原因,从而找到有效的解决办法。自Page以来,大量的研究都致力于变点分析这一理论及其在各个领域中的应用[1]。在现有的方法中,Cusum检验因其在实际应用中的易用性而长期流行,与似然法相比,原序列真实分布未知情况可使用Cusum方法。例如文献[2,3]。在金融和生物统计中,数据常具有尖峰厚尾的性质,尾指数是描述此特征的一个重要指标。实际应用中,大多数文献关注的是导致极端事件发生变化的均值或方差,但尾部的变化(即尾指数变化)会导致更多的极端事件。
极端现象的统计建模和分析是非常关键的,因为灾害和恐慌事件(如洪水、大地震和股市崩盘)的潜在风险可以事先确定,从而使它们得到充分的管理或预防。在此基础上,研究极值理论中的变点检验问题,特别是由于尾指数代表分布的肥胖程度,并确定了样本最大值等极值渐近分布的形状,因此本文重点研究分布尾指数的变点检测。尾指数估计问题是几十年来统计、金融、水文[4]、可靠性和通信工程中的一个核心问题。Quintos et al.和Kim et al.发展了一种检测分布尾指数参数变点的方法,这两种方法都是基于Hill的尾指标估计,都是针对厚尾分布而进行的[5,6]。根据Lee et al.提出的检验程序,考虑尾序过程,构造Cusum检验并证明尾序列过程在假设尾指数保持为常数的原假设下弱收敛于布朗运动[7]。
本文将根据Oka et al.提出的变点估计修正单分位数方法进行样本尾指数变点检测,利用Cusum检验思想,主要是针对多元时间序列尾指数变点检测[8]。采用单分位数方法对多元时间序列进行样本尾指数变点检测。文章主要从以下方面进行:首先,进行模型基本假设介绍、检验统计量的构造和统计量极限分布的证明;其次,变点存在性检验及临界值的模拟计算;然后,针对三个经典厚尾分布类型模拟数据进行模拟研究,最后,利用本文提出的方法对深圳市香蜜湖路市委党校南行路段车流量数据进行变点存在性研究分析。
1 模型理论介绍
1.1 模型基本假设
利用变点检测模型检测多元时间序列中样本尾指数的变化,我们假设所有随机变量都被定义在概率空间(Ω,P)中。假设样本观测值为{Zit,i=1,…,n,t=1,…,T}是一个非负随机变量序列,其i是指某个个体(如:年),t是指时间(如:天)。设m是将样本划分为m+1段的m个未知变点,及T1,…,Tm为对应未知变点。对于每个i,假设Zit~fj,对于t∈[Tj-1,Tj),j=1,…,m+1,其中T0=1,Tm+1=T+1,fj是其分布函數,使得fj在实际应用中不同于fj-1和fj+1。为了避免估计的序列样本量过少,进行变点检测时默认对原序列存在以下可能的划分:Λε={(T1,…,Tm):Tj-Tj-1≥εT,T1≥εT,Tm≤(1-ε)T},其中ε>0是个较小的常数。Kim et al.提出的基于累积和检测时间序列尾指数变化的模型,将其应用到多元时间序列尾指数变点检测中。尾指数是衡量样本尾部分布的肥胖程度的指标[9]。对于该变点检测问题,有如下假设:
2 变点存在性检验
2.1 变点存在性检验步骤
由尾指数计算公式得出的各样本尾指数情况如表1所示,可以看出在样本的参数变化时其尾指数也随之变化。 但在实际情况下,我们是无法从散乱的数据中观测到该变化。下面的模拟研究中我们将针对上述三个类型分布数据中检测其尾指数的变化,即尾指数变点存在性检验。
3.2 临界值的确定
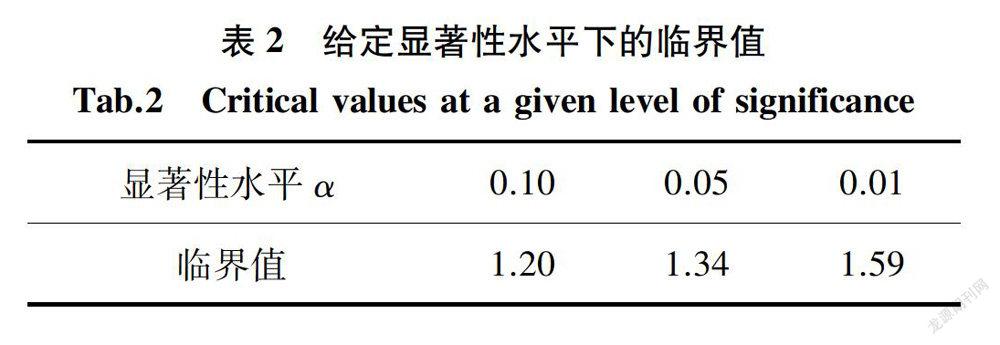
检验统计量的极限分布性质检测尾指数变点存在情况,由于临界值通过其极限分布不容易计算,所以通过蒙特卡洛模拟(Monte Carlo simulation)方式获得检验法则中的临界值,即在给定显著性水平为α的条件下,分别产生随机数εi,且εi~N(0,1)样本量为1000,模拟10000次,α分别取01,0.05,0.01,计算μn,1,得到10000次模拟最大值的(1-α)分位数即为对应α水平下的临界值,其结果展示如表2。
由上表可以看出单分位数方法对多元时间序列尾指数变点检测在显著性水平α=0.05下准确度相对最高,且针对三个分布类型数据当分布从正态分布变化到t分布时检测正确率很高,说明该方法针对分布变化导致尾指数变化情形的变点识别更加精确,且运算速度较快,尤其对于t分布的检测时间比其他两种分布都少。
对于多变点检测,本文采用二分法原理,结合二分法来对变点个数和位置的估计简单描述如下: 第一步,通过上文所述变点存在性检验方法在全部数据集{Zit}上检验变点是否存在,若没有变点则终止程序,表明整个数据集不存在变点; 否则,我们可以估计出第一个变点T^1。第二步,基于变点T^1将数据序列{Zit}分为两个子集{Zit}T^1-1t=1与{Zit}Tt=T^1,则类似地用同样的方法检验子序列{Zit}T^1-1t=1和{Zit}Tt=T^1中是否存在变点,并且相应地进行位置估计。无论何时,若不能检验出某个子序列存在变点,则说明这个子序列中不存在变点; 若检验出了变点,则继续利用二分法将该序列分开,再在每个子序列中检验是否存在变点并进行位置估计。一直持续上述过程,直至所有子序列中不再检验出变点为止。运用此方法,仅需要比较子序列没有变点和仅有一个变点的模型,并且可同时确定变点的个数和它们的位置,因而该方法简单而有效。
4 实例分析
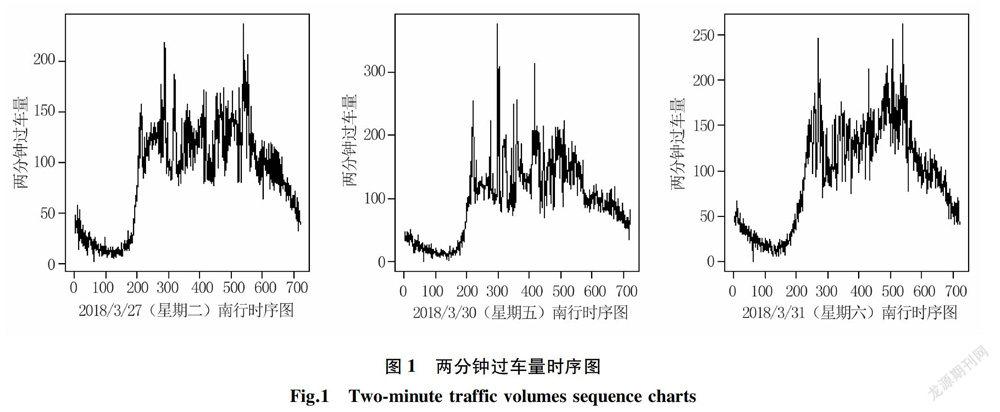
本实例分析数据源于深圳市局部区域道路的流量监测数据,主要选取深圳市香蜜湖路市委党校南行路段2018年3月27号(星期二)、2018年3月30号(星期五)和2018年3月31号(星期六)三天的数据为例,数据结构为每两分钟记录一次该路段车流量总数(一天共720个数据),根据实际数据得到过车量的时序图1所示。
分别以深圳市香蜜湖路市委党校南行路段2018年3月27号(星期二)、2018年3月30号(星期五)和2018年3月31号(星期六)三天的数据为例,利用本文的单分位数方法根据二分法原理将多变点转化为单变点问题进行变点检测,得到结果如图2、图3所示。
由图2(左)显示深圳市香蜜湖路市委党校南行路段2018年3月27号(星期二)车流量变点检测情况,检测结果显示存在三个变点,对应的位置分别是205、274、555,相对应的时间为 06∶46,09∶04、18∶26,2018年3月30号(星期五)车流量变点检测情况如图2(右)所示,检测结果显示存在四个变点,对应的位置分别是199、217、512、550且相对应的时间为 06∶34,07∶10、17∶00、18∶16,从检测结果容易看出工作日星期二和星期五有着类似的交通流变化规律,检测出早高峰7∶00~9∶00和晚高峰17∶00~19∶00都存在交通流变点,对于星期五而言变化情况更为复杂,这是因为星期五是一周中工作日的最后一天,人们都有各自的周末安排,在结束一周的工作后将出行旅游或者和朋友聚餐等活动,这就造成交通流变化规律有一定的变化,本文的检测结果和人们平时的出行规律相符合,证明了此方法的有效性。
2018年3月31号(星期六)车流量变点检测结果如图3所示。
从图3中2018年3月31号(星期六)车流量变点检测结果得到,在周末变点存在的时间为8∶22,15∶50,17∶56和上述工作日车流量变点检测结果相比,周末的早高峰要比工作日来得晚,而晚高峰变点存在情况和工作日相差不大,这是因为周末是人们在经过辛苦的一周工作后放松的时间,人们的生活习惯倾向于更加随意和散漫,人们都更愿意睡个舒服的懒觉再整理出门,这就导致了路段交通流变点的延迟,说明本文变点检测方法能有效地检测出交通流变点存在情况。
5 总结
本文通过单分位数方法对多元时间序列尾指数变化进行变点检测。通过模拟研究证明了该方法的有效性,通过对交通数据的实例分析,得到该方法能准确检测到交通流中存在的变点,进而对于出行者而言了解该信息可以避免出行高峰期,提高出行效率,对于相关交管部门而言可根据该信息有效且快速地采取解决方案,一定程度上舒缓交通压力。
参考文献:
[1][1]Page E S. Continuous inspection schemes [J]. Biometrika, 1954, 41: 100-116.
[2]Brown R L. Techniques for Testing the Constancy of Regression Relations Over Time[J]. Journal of the Royal Statistical Society, 1975, 37(2):149-192.
[3]Lee S, Nishiyama Y, Yoshida N. Test for Parameter Change in Diffusion Processes by Cusum Statistics Based on One-step Estimators[J]. Annals of the Institute of Statistical Mathematics, 2006, 58(2):211-222.
[4]白乙拉,劉国庆,李志军,等.芬兰Valkea-Kotinen 湖5月-10月水温长期变化趋势分析[J].渤海大学学报(自然科学版),2018,39(4):289-295.
[5]Quintos C, Fan Z, Philips P C B. Structural Change Tests in Tail Behaviour and the Asian Crisis[J]. Review of Economic Studies, 2001, 68(3):633-663.
[6]Kim M, Lee S. Test for tail index change in stationary time series with Pareto-type marginal distribution[J]. Bernoulli, 2009, 15(2):325-356.
[7]Lee S, Ha J, Na N S. The Cusum Test for Parameter Change in Time Series Models[J]. Scandinavian Journal of Statistics, 2003, 30(4):781-796.
[8]Oka T, Qu Z. Estimating structural changes in regression quantiles[J]. Journal of Econometrics, 2011, 162(2):248-267.
[9]Kim M, Lee S. Test for tail index change in stationary time series with Pareto-type marginal distribution[J]. Bernoulli, 2009, 15(2):325-356.
[10]Dupuis, Debbie J. Modeling Waves of Extreme Temperature: The Changing Tails of Four Cities[J]. Journal of the American Statistical Association, 2012, 107(497):24-39.
(责任编辑:曾 晶)

