做更专业的教师
张红娜

【摘要】本文围绕“小学数学‘厚重课堂的探索与实践”这一课题的研究,从引领教师做“厚重教师”这一角度出发,借助“教师专业知识考试”试题命制这一载体,通过对部分试题命题意图的分析,引领教师进一步“学课标、通教材、读学生、研教法”,使教师的专业素养更加“有高度、有广度、有深度、有灵活度”,形成正确的教师专业成长导向。
【关键词】厚重教师 专业知识考试 专业素养提升
2010年,我们提出了“厚重课堂”的教育思想和教学主张。多年来,我们组织全市学科教师,围绕河南省教育科学“十二五”规划重点课题——“小学数学‘厚重课堂的探索与实践”进行了系列化研究,研究成果获得了省基础教育教学成果一等奖。
该课题着重围绕小学数学“厚重课堂”所应具备的课堂教学质量标准(追求“五感”——情感、实感、动感、灵感、效感;突出“五味儿”——数学味儿、生活味儿、文化味儿、趣味儿、人情味儿)展开。达到该研究目标必备的前提和保障则是要求教师“厚练功底”“厚研教材”“厚读学生”“厚析课堂”“厚积反思”,从而做一名“厚重教师”,这是该课题实验要突破的难点。所以,在课题实验的过程中,我们重点围绕如何突破课题的“难点”开展工作,引领广大教师具有做“厚重教师”的意识和行为。
2018年,我们组织全市小学数学教师进行了“教师专业知识考试”,整套试题分“专业知识”和“教材教法”两大部分。在试题命制的过程中,我对“厚重教师”的内涵又有了深刻的理解,对如何引领一线教师做“厚重教师”也有了更加明确的思路。本文试结合此次专业知识考试的部分试题,谈谈命题时的真实考查意图,期望我们都能做更专业、更厚重的教师。
一、专业知识部分——让教师的专业功底更厚实
“专业知识部分”的命题围绕义务教育阶段的数学教学内容展开,遵循《义务教育数学课程标准(2011年版)》的要求,依照义务教育阶段的教材(人教版)编排,重在考查课标中提出的“十大核心概念”,力求使教师的专业素养更加“有高度、有广度、有深度、有灵活度”。
1.有高度
【典型试题】
操作:
(1)通过示意图表示出平行四边形、矩形、正方形、菱形之間的关系。
(2)作图中圆的内接正方形和外切正方形。(保留作图痕迹)
解答或证明:
(1)发现规律,并证明规律。
15×15=1×2×100+25
25×25=2×3×100+25
35×35=3×4×100+25
45×45=4×5×100+25
……
规律:(a×10+5)2= 。
规律证明:
(2)证明:三角形的外角等于与它不相邻的两个内角之和。
(3)我国古代数学名著《孙子算经》中记载了这样一道数学趣题:“今有雉(鸡)兔同笼,上有三十五头,下有九十四足,问雉兔各几何?”请你分别用下面三种不同的方法解答这个问题。①算术方法(假设法);②一元一次方程的方法;③二元一次方程组的方法。
【考查意图】
在“厚重课堂”的研究过程中,我们要求“厚重教师”在学科知识上要做到三“通”——“通晓”相关学科的知识;“通览”本学科的知识;“精通”本学段的知识。针对小学数学教师提出明确要求:“居高临下教小数”。因此,本次试卷中涉及一定量的中学数学知识,我们称其为“上位知识”。如:上述试题中的“菱形”“内接正方形和外切正方形”“证明”和“一元一次方程、二元一次方程组”等均涉及“上位知识”。这些知识,不要求小学生了解,但从事小学数学教学的教师们一定不能忘。因为,有了它们,我们的教学就站在了一定的高度,不同学段的学科知识之间的联系就会更加紧密,学生后续知识的发展就会更加脉络清晰。有了这样的“大教材观”和“学科知识观”,教师的专业功底就会更加扎实,数学课程标准的理念就会得到更好的落实。
2.有广度
【典型试题】
填空:
(1)边长是1000米的正方形的面积是1平方千米,边长是100米的正方形的面积是1公顷。你知道吗?边长10米的正方形的面积是1( )。加上它的话,所有相邻两个面积单位之间的进率都是100。
(2)教材中介绍了2、3、5的倍数的特征。你知道吗?4的倍数具有的特征是( )。
判断:
(1)当一个物体两个部分的长度的比大致符合 0.618∶1时,常会给人优美的视觉感受,所以我们把“0.618∶1”称为“黄金比”。 ( )
(2)“哥德巴赫猜想”的内容与质数、偶数有关。( )
(3)最早提出“用算筹区分正负数”的数学家是祖冲之。( )
【考查意图】
以上试题是对教材内容的拓展,旨在拓宽教师的专业知识面,了解更多相关的数学文化,使教师的专业知识更宽泛,真正做到“给学生一碗水,教师 要有一桶水,甚至长流水”。
3.有深度
【典型试题】
操作:
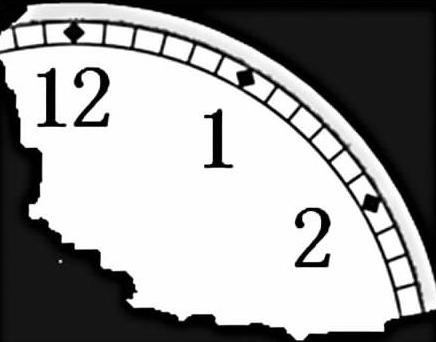
下图是一个残破的钟面,请在钟面上选择合适的两点连成一条线段,使其长度正好等于该圆形钟面的半径。(先画出线段,再说明理由)
【考查意图】
此题连接“12”和“2”所成的线段正好是该圆形钟面的半径。因为,想象如果是一个完整的钟面,点“12”“2”与圆心三者顺次连接组成一个三角形,它正好是頂角(以圆心所在的角)为60°的等腰三角形(两腰分别为半径),则可推理出该三角形为等边三角形,所以两点之间的线段之长正好与半径相等。此题如果考查学生,是有相当大难度的。但考查学科教师,还是有一定价值的。除了考查教师综合运用学科知识解决问题的能力,还能增强教师的空间观念、想象能力、推理能力、应用意识和创新意识等,使学科核心素养落实到位,同时引领教师在专业知识的“精”“深”上下功夫。
4.有灵活度
【典型试题】
判断:
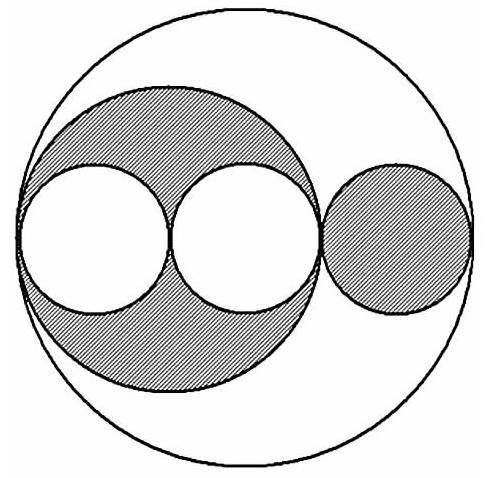
如下图,将三种不同直径的五个圆组合在一起,并让其中一些圆彼此相切。整个图中阴影部分的面积是13.2cm2,整个图中空白部分的面积是( )cm2。
A.13.2 B.26.4 C.39.6
【考查意图】
此题图中小、中、大三种圆均没有给出半径或直径的具体数据,只给出了阴影部分的总面积,按照正常的解题策略,应该是无从下手。如果换个角度来思考,此题便可迎刃而解:由小、中、大三种圆半径之比为1∶2∶3,可知三者面积之比为1∶4∶9,阴影部分的面积一共是其中的3份(中圆的阴影部分是2份,再加一个阴影小圆),则空白部分为其余的6份,正好是阴影部分的2倍,所以面积为26.4cm2。这样的解题策略,不仅省时,而且高效。最重要的是,提醒数学教师:数学问题的解决除了要遵循规律,还要善于在“换个角度看问题”中学会机智多变,不断培养思维的灵活性和敏捷性。
二、教材教法部分——让教师的教学素养更厚重
“教材教法部分”的命题重点围绕“课标、教材、学情和教法”等几个方面展开。借助试题的命制和考查,引领教师进一步“学课标、通教材、读学生、研教法”,厚练教学功底,提升学科素养,形成正确的教师专业成长导向。
1.学课标
【典型试题】
填空:
数学是研究数量关系和空间形式的科学。新课标将数学课程内容划分为四大领域。比如:“角的初步认识”属于( )课程领域; “平均数”属于( )课程领域;“20以内的进位加法”属于( )课程领域;“自行车里的数学”属于( )课程领域。
判断:
(1)新课标要求“综合与实践”的教学应当保证每学期至少一次。( )
(2)新课标提出的“四基”指的是“发现问题、提出问题、分析问题和解决问题”的四种基本能力。 ( )
(3)演绎推理用于探索思路,发现结论;合情推理用于证明结论。( )
简答:
新课标在“评价建议”中指出,“可以对部分学生采取‘延迟评价的方式”。请谈谈你对“延迟评价”意义的理解或实践。
【考查意图】
新课标是教师教学的纲领性文件。学习课标,是教师从事教学的重要前提和保障。教师只有对课标了然于心,才能正确理解学科教学理念,整体把握学科教学全局,有的放矢地贯彻落实。因此,对新课标的学习,我们提出了“反复学”的要求,不仅要“学懂”,还要“学深”“学透”,要贯穿在日常教学的全过程。我们曾以“你对新课标知多少”为主题,面向全市学科教师组织过教学基本功比赛活动,先后两次对新课标进行过深度学习。上述试题只是新课标学习考查中的少部分内容,期望通过不间断地考查,提醒教师不间断地学习课标。
2.通教材
【典型试题】
填空:
(1)人教版教材在各个年级都编排了“解决问题”的专项内容。其中,低年级的编写体例一般是:知道了什么?——怎样解答?——( );
中高年级的编写体例一般是:( )——分析与解答——回顾与反思。
(2)在人教版教材的编排体系中,关于“分数”和“小数”的学习,小学里主要经历了两个阶段。第一学段安排了“初步认识”:编排顺序是( );第二学段安排了“再认识”:编排顺序是( );(写出相关的单元名称及所在教材的册数即可)
(3)整数、小数、分数的加减法,其算理是相通的,即( )。
(4)长方体表面积的计算方法与圆柱体表面积的计算方法具有内在的统一性,都可以用( )方法来计算。
简答:
分数的基本性质与小数的基本性质有什么关系?请举例说明。
【考查意图】
上述前两道填空题分别从人教版教材专项内容的“编写体例”、相关知识的“编排体系”等方面进行了考查,后面几道题就知识点之间的联系进行了沟通。通过这些有代表性的“典型试题”,我们提醒并强调学科教师要意识到——“通教材”很重要。
3.读学生
【典型试题】
简答:
(1)教學“3的倍数的特征”一课前,学生认为“3的倍数的特征”可能是什么?为什么会有这样的想法?
(2)“平行四边形的面积”教学过程中,在“数方格求面积”这一环节,如果不给出“不满一格按半格算”的提示,学生能否在方格图中准确数出平行四边形的面积?
(3)学生在作业中这样简算下面的试题,你怎么评判?
0.25×125%×32 0.25×125%×32
= ×32×1.25 = × ×32
=8×1.25 =10
=10
【考查意图】
学生是我们教学的对象,也是教学的重要依据。在“厚重课堂”课题的研究中,我们提出了“厚读学生”的要求。从“课前、课中、课后”三个角度研读学生的知识基础、学习状态、真实思维等,为教学起点的选择、决策的调整、走向的把握等提供重要依据。如上述第1题:如果课前走进学生,就会发现受“2、5的倍数的特征”影响,多数学生认为“个位是0、3、6、9的数是3的倍数”,那么,教师的教学起点就可以从学生的“错误初念”开始展开,实现“以学定教”。第2题中,如果不给出“不满一格按半格算”的提示,相信部分学生是可以通过“平移”凑成整格进而顺利数出面积来的。这一“招”,恰是下一步推导面积计算公式的重要“手段”。所以,教师在此环节要充分相信学生并大胆放手,通过生生之间的相互启发让“数方格”求面积与“剪拼割补”求面积自然对接,水到渠成,实现真正意义上的“顺学而导”。第3题针对学生作业中出现的“非常规”现象,教师应该了解学生的真实想法,肯定他们的创新思维,进行客观公正的评判,让教学变得更加“个性化”和富有“人情味儿”。
4.研教法
【典型试题】
判断:
教学三角形的“稳定性”最好的方法是让学生通过学具体验其“拉不动”。( )
简答:
如何借助“几何直观”帮助学生思考、解决下面的问题。
计算: + + + + + +…=
【考查意图】
教学有法,但无定法,贵在得法。教学方法是帮学生搭建从“不知”到“知之”的桥梁。因此,“得法”显得尤为重要。很多教师教学三角形的“稳定性”的“得法”就是让学生通过学具体验其“拉不动”。
通过对上述试题的分析,我们对教师学科素养的提升有了更明确的目标和更清晰的思路。“学科教师是学生能直接观察到的学科形象。”因此,作为教师,我们要修炼我们的“职业气质”,更要修炼自己的“专业气质”。要爱自己从事的教学专业,更要学会“专业地去爱”。要“用纯净的心,做专业的事”,努力厚重自己的学科素养,为自己从事的专业做好“代言人”。
注:本文为河南省教育科学“十二五”规划2011年度重点课题“小学数学‘厚重课堂的探索与实践”(课题编号:[2011]-JKGHBB-0716)研究成果之一。

