题感
——一种重要的数学活动经验

王成杰 刘新春

(1.江苏省扬中高级中学212200; 2.扬中市教师发展中心212200)

1 引言

经常听到一些学生平时考试或高考后说，这次考试不在状态，平时会的方法都想不起来，一走出考场就会了.还有一些学生说，这次考试感觉特别好，做得很顺手.这些现象其实描述的就是解题的感觉，简称题感，所谓题感就是对数学问题的感知、预感、灵感，能直觉感知问题的求解思路和解法，是在解题中产生的特有的感觉.从更上位的观点来看，题感是数学直观的具体体现，史宁中教授认为：数学教学的根本，那就是培养学生的数学直观，因为数学的结论是“看”出来的，不是证出来的，依赖的是数学直观.“看”就是一种直观感觉.日本数学家小平邦彦也认为，数学就是一种感觉.题感好主要表现在：首先是具有敏锐的洞察力和预见性，能抓住本质，预感解题方向，迅速发现解题突破口，预测解题方法，对问题的解决方法达到直觉、顿悟的程度；第二，能感知解决问题思路的优劣，甚至能一眼发现问题中的错误，预见某些解题思路繁琐甚至无法解决问题；第三，能善于运用直觉思维、逆向思维、发散思维、简缩思维、整体思维等思维形式思考问题，遇到挫折能够及时调控思维，调整思考方向，对自己的思维过程能够自觉地反思、梳理，保存最简捷的思路和方法.题感好的最高境界是不断产生灵感，灵活自如创造性地解题.灵感来自何处？一方面，陈省身先生认为，灵感完全是苦功的结果，要不灵感不会来.换句话说灵感就是朝思暮想，如果你特别想解决一个问题，你走路、吃饭、睡觉、活动都在想着这个问题，灵感就很容易找上你，因为你目标明确，你的潜意识就会一直去帮你找答案，想办法，就容易产生灵感.另一方面，灵感可能是简缩思维与直觉思维的聚合与突变.简缩思维其实就是抓住本质、规律，抓住主要矛盾，摒弃细枝末节，简化思维链.而直觉是对问题的“顿悟”和“猜测”，直觉来源于经验与激活思维的某些诱因，如坚实的基础知识、数形结合获得的影像，以及对称等美感，直觉思维会被以上诱因触发，突然间领悟了某些道理或获得某些启示得到思路、方法、答案.

2 数学题感：在活动中产生

2.1 在知识理解中萌生

题感好首先建立在对基础知识的准确、深刻、全面理解，对数学思想方法的深刻把握和对数学思维的灵活运用.没有必要的数学基础知识作为基础，数学思想方法就没有载体，思维也就无法附着.数学思维离不开数学语言，而数学语言首先是由数学概念、符号、图形构成的，数学概念必须从大量的实际现象中，通过观察、比较、联想、概括、抽象形成概念，并通过正例强化和反例辨析才能更加深刻地理解概念，才可能具有更强的迁移性，更快捷地运用到解题中.数学定理、公式、法则和正确结论只有弄清了它的来龙去脉、推导方法和各种变形，才能灵活运用于解题，而数学思想方法则渗透在概念的形成与迁移、公式定理的猜想与发现、证明与变形、解题思路的分析突破之中，有了坚实的基础知识和融会贯通的思想方法，数学思维才能顺向快捷，逆向灵活，遇挫调控，多方发散，有机激活，甚至激发灵感产生.

案例1如图，E，F分别是边长为4的正方形ABCD的边DC，AB的中点.半径为1的圆O的圆心与正方形的中心重合，过AB边上一点P(0≤AP≤1)作圆O的切线，交边BC于点Q点，过Q点作圆O的另一条切线，交EF于点N.问是否存在常数m,使得mQN+NE为定值？ 如果存在，请求出常数m，并给出定值，如果不存在，请说明理由.

分析：从一般经验看，涉及直线与圆相切问题通常可建立直角坐标系，运用解析几何知识解决，从而得到一般方法.

解以A为原点，AB所在直线为x轴，建立平面直角坐标系．

设PA=a，则P(a,0),0≤a≤1，

设PQ的斜率为k，则PQ方程为y=k(x-a)，

令x=4得Q(4,k(4-a))，

因为点O在直线PQ上方，

设NQ的斜率为k1，

则NQ方程为y-k(4-a)=k1(x-4)，

令x=2得N(2,k(4-a)-2k1)，

所以NE=4+2k1-k(4-a)，

由NQ与圆O相切，

因为点O在直线NQ下方，

=2[-2k1-2+k(4-a)]，

所以mQN+NE

=2m[-2k1-2+k(4-a)]+4+2k1-k(4-a)

=(-2m+1)[2+2k1-k(4-a)]+2,

思考：观察以上解法，感觉运算量比较大，且运用知识的方法是“直译”知识，没有触及知识内核与问题本质；另一方面从图形直觉看，从正方形以及直线与圆相切的条件中可以发现许多垂直关系，且圆心是一个重要特征，如何将这些条件整合起来，找到一种更为简捷的本质关系？题感开始发挥作用了：

从这一解答的思维活动过程可以看出：对原有解法的不满意是产生题感的源头之一，扎实全面的数学知识是基础，将各个知识点的本质融合，加上一定的解题活动经验，通过不断地观察、尝试、思考，激活灵感，可能产生更加简捷的解法，印证和形成题感.

2.2 在解题训练中生长

学生通过恰到好处的训练能够深刻感悟解决数学问题的全部过程，学会正确审题，制定解题计划，分析解决问题的思路，迅速找到解决问题的突破口，准确选择简捷的方法解决问题，甚至创造方法求解问题，反思总结解题规律. 在解题教学中比告诉学生解题方法更重要的是指导学生自主探究解题思路，知道怎样找到解题思路，如何寻找题眼(即解决问题的突破口)，如何比较各种解法的优劣以及适用范围.如何将问题推广到更一般的情形，如何对问题逆向探究，如何将解题方法简捷优化、类比迁移，触类旁通，举一反三.教师不仅要展示正确的解题思路，还要暴露教师解题中的思维过程、错误与困惑，不仅要展示学生在解题过程中的优美解法和思维闪光点，更要鼓励学生暴露解题过程中的错误，揭示形成错误的原因，还要善于从学生的错误中发现创新的萌芽.教师还必须重视对学生的解题方法和学习方法的指导，揭示知识与方法、技能之间的内在联系，把自己成功的学习经验和失败的教训及其形成的原因和盘托出，供学生借鉴.

(1)设动点P满足PF2-PB2=4，求点P的轨迹；

(3)设t=9,求证：直线MN必过x轴上的一定点(其坐标与m无关).

分析：(1)(2)略，着重寻找(3)的解题思路：常规的思路是分别求出两条直线与椭圆的交点，建立两个交点所在直线的方程，通过直线方程寻找定点得到方法1.(解法过程略)

从一般的解题经验，能否先猜出定点，再验证一般情况成立？可以从特殊情形出发发现定点位置：当直线MN与x轴垂直时可求得定点坐标然后再验证一般情形.(解法过程略)

从图形中发现，直线AT、BT与椭圆的交点，也是直线MN、x轴与椭圆的交点，而由求双曲线的渐近线方程的经验，可以将两条直线的方程写成一个二元二次方程，题感提示我们，能否不求交点坐标，借助椭圆的方程和直线AT、BT方程直接求出直线MN方程，经过尝试发现是可行的，于是得到方法3：

由于t=9，

即m(x+3)-12y=0

①

即m(x-3)-6y=0

②

将①与②左右两边分别相乘有

m2(x2-9)-6my(x+3)-12my(x-3)+72y2=0

③

④

可以证明④式即为直线MN的方程，

令y=0，则x=1，

即直线MN必过x轴上的一定点，

定点坐标为(1,0).

以上从直觉思维和简缩思维中产生灵感获得方法3，表明数学题感可以从解题训练中培养、强化，并逐步内化为解题活动经验.

(Ⅰ)求动点P的轨迹方程；

(Ⅱ)设直线AP和BP分别与直线x=3交于点M,N，问：是否存在点P使得△PAB与△PMN的面积相等？若存在，求出点P的坐标；若不存在，说明理由.

分析1:(Ⅰ)动点P的轨迹方程易得x2+3y2=4(x≠±1)，解题过程略.

以下着重分析第(Ⅱ)小题.

解法2：由S△ABP=S△PMN可得

由比例性质，它们在x轴上的投影比相等，可得

(xP-xA)(xP-xB)=(xN-xP)(xM-xP),

即(xP+1)(xP-1)=(3-xP)(3-xP),

上述两种解法瞄准了几何图形的局部和细节(边或角)获得解法.但从题感的角度运用整体思维和简缩思维就能跳出细节，着眼于从几何图形的整体结构出发，在△ADN中，从△PAB与△PMN的面积相等、B为AD中点、M为ND中点，结合分析得到P是△ADN的重心，由于点A,M,N的横坐标已知，因而能便捷地求出P点的坐标.

解法3：连结AB并延长交直线x=3于点D，

连结AN，要使S△ABP=S△PMN，

须且只须S△AMD=S△BND，

由于B为AD中点，

只须M为ND中点即可.

此时点P是△ADN的重心，

由三角形的重心坐标公式可得

2.3 在反思顿悟中升华

题感不是教师教出来的，而是学生悟出来的.怎么悟，就需要解题.题感好必须不断悟题，一悟问题的条件之间、条件与结论之间的多向联系，比较差异，发现关系，寻找桥梁.二悟条件、结论与数学基础知识之间的联系，众多问题往往是“题在书外，根在书上”，即用书本知识解读条件、结论.三悟问题中条件、结论与数学思想方法之间的联系，即用数学思想方法来联结条件与结论之间的关系——解题思路.四悟解决问题失败的原因与成功的体验.五悟本题的解法与大脑中已有知识方法的关联.悟题的体验状态至少有三种层次：第一，只可意会(有时连意会都做不到)不能言传，捉摸不定，视之无形，百思不得其解.第二，一梦醒来，茅塞顿开，豁然开朗，浮想联翩，妙不可言，内心澄明，思维清澈，心灵共鸣.第三，唤醒沉睡的潜能，激活封存的记忆，开启封闭的心智，放飞禁锢的思维.

以上是学生的常见解法思路，是解题基本经验发挥了作用，一般情况下，本题的教学过程就结束了.这时指导学生反思以上解题过程，本题解法其突破口是从三角形的面积出发借助直线方程构建三角形面积与坐标之间的联系，而表示三角形的面积有多种形式，如

等等，题感提醒我们，能否不设直线方程，直接建立三角形面积与坐标之间的关系？学生经过反复思考讨论发现：

从表示面积的第三个公式可以发现，

两式相乘即有

展开得

配方得

即有

(b2x1x2+a2y1y2)2+a2b2(x1y2-x2y1)2=a4b4,

而此式正好含有三角形面积的表示形式，

联想结论

(b2x1x2+a2y1y2)2+a2b2(x1y2-x2y1)2=a4b4，

代入可得

化简得2x1x2+3y1y2=0，

即2x1x2=-3y1y2，两边平方消去y1,y2得

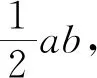
3 数学题感：一种活动经验

数学基本活动经验通常是指在数学目标的指引下，经历了实际操作、直观想象、归纳演绎、抽象概括、逻辑推理等数学活动过程，从量变到质变飞跃时形成的对相关数学活动起指导作用的认识、体验和观念，是学生在学习过程中获得的对数学知识、技能、思想之间如何联系的一种直观感受，是学生发现数学问题与知识、技能、思想之间联系的桥梁.数学基本活动经验的核心是思维活动经验.获得数学基本活动经验的过程大致可分为：经验萌发、明晰、概括、重构等阶段.解题活动是高中数学教学中的主要形式之一，良好的题感是数学活动经验的重要组成部分，对于学生积累数学活动经验具有很好的促进作用.因为题感是一种感觉、习惯和思维方式，也是一种经验，既有感性经验，又有理性经验，既来之直接经验，又取之间接经验.题感在数学知识的形成理解中萌生，在发现、提出、分析、解决数学问题的过程中生长，在反思顿悟中成熟，而这一过程正是帮助学生获得数学思考的基本活动经验的过程.一题多解或多题一解是训练学生解题灵感、解题策略和解题习惯的主要形式，也正是增加数学活动经验的载体.形成良好的题感就是获得数学活动经验,反之，题感根植于经验，数学活动经验丰富的学生的题感通常也比较优良.

培养学生良好的题感是培育数学核心素养的重要组成部分.题感基于解题的感觉，首先是直觉思维起作用，要求一眼就能看出问题的解答思路或答案，这是直观想象素养好的标志.面对大量的题目信息，学生能够快速整理提取、选择、连接，迅速找到核心——解题思路，这是数据分析素养的基本要求.对问题进行预判、调控、优化是促进逻辑推理素养的有效途径.把实际问题顺利转化为数学问题并能合理制定优化的解题策略，选择和创造快捷的方法解决问题，这是训练数学建模素养的主要环节.因此培养良好的题感是培育数学核心素养的重要组成部分.

数学题感是一种神奇的力量，是直觉洞察的结果，是思维习惯的结晶，是反思顿悟的升华，它在学习数学知识的过程中产生，在解题训练在成长，在反思顿悟中完善，逐步形成丰富的数学活动经验，并内化为数学素养.