透视分步突破，深度变式探究

王雷 葛艳

[摘  要] 函数综合题是中考数学的重点题型，其中不仅包含众多的函数曲线，同时涉及一些关键的知识联系点，因此可以充分考查学生的知识能力. 解析问题时，需充分挖掘问题本质，从知识联系性出发选取合适的方法，文章以一道函数综合题为例，进行分步突破，解后思考，并提出相应的教学建议.

[关键词] 一次函数;反比例函数;线段;点坐标

考题呈现

试题（2019江苏泰州中考）已知一次函数y1=kx+n（n<0）和反比例函数y2=■（m>0，x>0）.

（1）如圖1，若n=-2，且函数y1，y2的图像都经过点A（3，4）.

①试求m和k的值;

②请直接写出当y1>y2时x的取值范围.

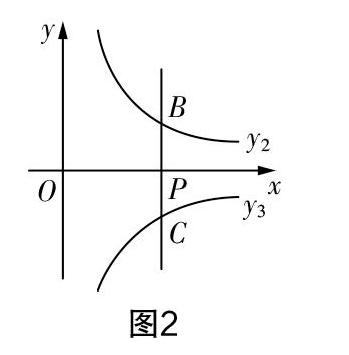
（2）如图2，过点P（1，0）作y轴的平行线l与函数y2的图像交于点B，与反比例函数y3=■（x>0）的图像交于点C.

①若k=2，直线l与函数y1的图像交于点D，当点B，C，D中的一点到另外两点的距离相等时，试求m-n的值;

②过点B作x轴的平行线，与函数y1的图像交于点E，当m-n的值为不大于1的任意实数时，点B，C之间的距离与点B，E之间的距离之和d始终是一个定值，求此时k的值及定值d.

分步突破

上述考题是中考常见的函数综合题，以一次函数与反比例函数为命题背景，涉及求函数解析式、取值范围和距离分析，以及定值求解等，由于考题有两问，每一问又细分为两小问，均含有各自的主干信息，所以下面对其分步突破.

1. 第一步：解构函数，巧定范围

题干给出了一次函数y1和反比例函数y2的解析式，对于第（1）问，设定n的值为-2，并给出了两函数的交点，所以第①问求函数解析式可以采用待定系数法，直接将点的坐标代入函数解析式即可. 将点A（3，4）代入一次函数解析式y1=kx-2中，可解得k=2. 将点A的坐标代入反比例函数解析式y2=■中，可解得m=12，所以m的值为12，k的值为2.

第②问分析y1>y2时x的取值范围，属于函数背景下的代数分析. 对于条件“y1>y2”，在函数图像中的表现为一次函数位于反比例函数图像的上方，因此问题转化为分析一次函数位于反比例函数图像上方时对应的x的取值范围. 而点A是两函数图像的交点，是其分界线，显然点A的右侧部分满足要求，又点A的横坐标为3，因此当y1>y2时，x的取值范围为x>3.

2. 第二步：分类讨论，定值变形

第（2）问中添加了反比例函数y3，通过作y轴的平行线产生了交点B和C. 第①问中设定点D是直线l与函数y1的交点，于是可求得点D的坐标为（1，2+n）. 根据l与函数y2，y3之间的交点可求得B，C的坐标，即B（1，m），C（1，n）. 点B和点C位于x轴的两侧，根据题干要求，实际上就是分析其中的中点情形，显然有三种情形：情形一是点D是BC的中点，情形二是点B是DC的中点，情形三是点C是BD的中点. 需要对其进行分类讨论，且线段长就是两点的纵坐标的差的绝对值.

情形一，当点D是BC的中点时，有BD=CD. 又BD=m-（2+n），CD=2，所以m-（2+n）=2，即m-n=4. 满足限制条件，所以该情形存在，此时m-n=4.

情形二，当点B是DC的中点时，有DB=BC. 又DB=2+n-m，BC=m-n，所以2+n-m=m-n，解得m-n=1. 满足限制条件，所以该情形存在，此时m-n=1.

情形三，当点C是BD的中点时，有BC=CD. 因为BC=m-n，CD=n-（2+n）=

-2<0，不可能，所以点C不可能是BD的中点.

综上可知，对于第（2）①问，m-n的值为4或1.

第②小问设定点E是过点B的平行于x轴的直线与直线y1的交点，所以点E的坐标为■，m. 根据定值构建的思路可知，d=BC+BE，只需要将所涉及的点的坐标代入其中即可. 当点E在点B左侧时，有d=m-n+1-■，分析该式为定值时d和k的值，只需对式子进行变形，将其中的参数以乘积形式表现即可，于是d=（m-n）1-■+1，所以当1-■=0时，显然d的取值与m，n无关，此时k=1，d=1. 当点E在点B的右侧时，有d=m-n+■-1，分析该式为定值时d和k的值，只需对式子进行变形，将其中的参数以乘积形式表现即可，于是d=（m-n）1+■-1，所以当1+■=0时，显然d的取值与m，n无关，此时k=-1，d=-1，矛盾，说明此种情形不存在. 综上可知，对于第（2）②问，k=1，d=1.

解后反思

上述是对考题的解析突破过程，考题考查了求函数解析式、取值确定和分析线段长，涉及一次函数、反比例函数的基础知识，以及图像中交点的求解方法，下面对突破过程进行深入反思.

1. 解析中的关键步骤

考题分为两大问，无论是求取值，还是分析距离关系，均需要准确把握函数图像的位置关系，明晰函数的交点. 而对于每一小问，还需要把握其中的关键步骤，如第（1）②问在分析y1>y2时x的取值时，需要理解不等式与函数图像之间的联系，即y1>y2不仅表示大小关系，在函数中还体现为图像的上下关系，基于该内容就可以直接获得突破方法. 又如第（2）①问分析三点之间的距离相等关系，其关键步骤是结合限制条件对三点之间的位置关系进行讨论，并结合点坐标进行细化，这也是函数背景下线段长与点坐标关系构建的方法. 第（2）②问中的含参数的代数式的定值讨论，解析的关键步骤是对代数式进行变形，即实现参数部分的因式分解，从而可通过设零将其消去.

2. 值得学习的内容

中考压轴题的学习价值在于，可以从中提炼出问题突破的思路和方法，从而掌握同类题的突破方法. 以第（1）②问为例，求“y1>y2时x的取值范围”，其解析本质就是数形结合，同时可以提炼出不等式问题的转化方法——图像分析法. 而对于第（2）问，实际上均可以归结为函数背景下的线段长分析. 从解析过程可知，利用点坐标来描述线段长是问题突破的核心，這也是函数与几何之间的知识联系点. 因此，求解与几何相联系的函数综合题时，要充分把握“点坐标”这一中间媒介，实现几何问题的代数转化.

3. 关于考题的变式

开展考题变式不仅可以深化问题认识，还可以拓展学生的解题思维，下面是以本考题所涉及的两个核心价值内容展开的变式探究.

变式1 （基于不等式图像解析方法进行变式）已知点A（3，b）是一次函数y1=kx+n与反比例函数y2=■（m>0，x>0）在第一象限的交点，若不等式kx+n>■的解为x>3，试分析k的正负.

思路点拨 由不等式的解可知，当03时，y1位于y2上方. 显然可以绘制出相应的图像，从而可确定一次函数单调递增，即k>0.

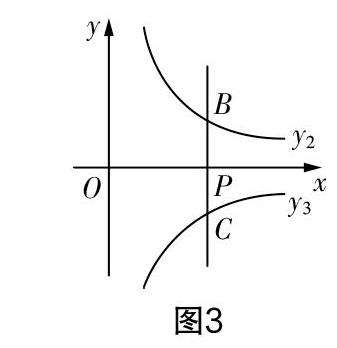
变式2（基于函数与几何的联系点进行变式）已知反比例函数y2=■（x>0），一次函数y1=-2x-2，如图3，过点P（1，0）作y轴的平行线l与函数y2的图像交于点B，与反比例函数y3=-■（x>0）的图像交于点C. 试分析在函数y1上是否存在一点D，使得∠BDC=90°. 若不存在，请说明理由;若存在，请求出点D的坐标.

思路点拨根据题干信息可求出B（1，12），C（1，-2），可将点D的坐标设为（a，-2a-2），在Rt△BCD中使用勾股定理可得BC2=BD2+CD2，然后利用点坐标可以分别求出线段长，基于线段长关系即可构建相应的代数方程，即可分析a是否有解.

■ 教学建议

1. 关注函数综合，解构曲线图像

函数综合题是中考的核心考题，一般因综合性强而解析难度大，实际上可以将函数综合看作是多条曲线之间的综合，因此解题时就可以通过分析曲线之间的联系点来加以突破. 而在日常教学中，需要教师对初中阶段所涉及的函数曲线进行系统归纳，包括一次函数、二次函数和反比例函数，让学生对函数的曲线特征、性质结构有一个充分的了解，能够根据函数解析式准确画出相应的图像，并能根据曲线之间的位置关系得出特征参数的值. 例如根据函数y1=kx+n（n<0）与反比例函数y2=■（m>0，x>0）相交可以得出k>0. 建立函数之间的图像联系是求解综合题的关键，也是数形结合策略分析问题的基础.

2. 重视突破方法，形成解题思路

综合题的突破除了需要具备扎实的基础知识外，还需要掌握相应的解析方法. 例如上述求解函数解析式所采用的待定系数法，分析距离问题时所采用的分类讨论和线段坐标化方法，正是在这些方法的灵活使用下才促使问题得到了解决. 因此，教学中需要教师对考题的解析方法加以总结提炼，让学生掌握根据考题特征选取合适方法的思路. 对于一些结构鲜明的考题，更应注重总结. 例如函数与几何综合题，应让学生把握函数与几何之间的联系点——点坐标，形成“函数解析式？圳点坐标？圳几何特征”的突破策略.

3. 注重考题变式，拓展数学思维

中考压轴题的问题形式多样，图像变化也十分灵活，所以开展考题教学时不能拘泥于问题本身，而应引导学生对背后的实质内容进行挖掘，并结合相关知识对其中的核心内容开展变式探究. 例如上述基于联系点对考题进行了不等式转化变式和几何特征变式，可使学生充分认识到函数图像与不等式、几何之间的关联. 而在变式探究过程中，则需要掌握适度原则，不能因变式不足使得探究无意义，也不能因过度变式造成超纲超范围的现象. 在变式探究的过程中，学生的数学思维可以得到锻炼，能促进学生创新思维的形成.