两类非线性方程(组)的对称约化和精确解
孙世飞 李雪霞 刘汉泽
(聊城大学 数学科学学院,山东 聊城 252059)
0 引言
随着非线性科学研究的不断发展,在数学物理领域中构造非线性方程组并得到其精确解已经成为了一项热门课题,包括非线性常微分方程(组)[1]、非线性偏微分方程(组)[2-4]和非线性差分方程(组)[5]如浅水波方程[6]、正则长波方程[7]、Drinfeld-Sokelov-wilson(DSW)[8,9]方程组等的研究都可以用来描述物理等其他领域的复杂现象,在诸多非线性方程和方程组的研究中,量子力学领域中重要的Schrödinger方程的多种精确解的研究也有着其重要的研究意义.
Schrödinger方程是由奥地利物理学家Schrödinger提出的用来描述微观粒子运动的量子力学中的一个基本方程,通过对每个微观系统的Schrödinger方程进行研究可以得到波函数的具体形式以及对应的能量,进而了解微观系统的性质. 非线性Schrödinger方程在非线性光纤、非线性光器件、光子晶体等多种非线性介质中作为可以描述非线性波动传播动力学的基本模型被广泛关注和研究、针对引入随机变量的各种修正的Schrödinger方程,采用解析和数值方法研究其孤子解具有现实意义;通过解析和数值的研究光孤子脉冲的动力学特性,可以进一步的研究光孤子脉冲在全光技术中的物理机制;通过相空间分析Schrödinger方程还可以对混沌动力学进行研究,通过研究基于非线性光纤和光纤器件的混沌动力学,可以寻找混沌出现的条件,而这些条件也在全光通信中为混沌加密等方向的研究提供了潜在的重要作用.
研究了如下形式的二阶CNS方程和三阶NLS方程两类不同阶数的非线性偏微分Schrödinger方程
iut+αu|u|2+uxx=0,
(1)
iut+uxxx+6|u|2ux+3u(|u|2)x=0,
(2)
其中α是系数,u是复函数振幅.Schrödinger方程在数学物理领域中是一种经典并且重要的非线性方程,但是由于非线性方程的复杂性和特殊性,目前并没有统一的计算工具和方法,在过去的几十年中,出现了很多求解非线性方程的一般方法,例如Hirota双线性方法[10,11]、辅助函数法[12,13]、F-展开法[14,15]、Exp-函数法[16,17]和李对称法[18-20]等,其中孙艳波采用不同形式的Hirota双线性方法对方程进行求解.通过位势变换引入新函数,将原方程转换成双线性导数方程进行求解[11];蔡国梁, 张风云等人用扩展的F-展开法求耦合Schrödinger-Boussinesq方程组的精确解;阮航宇利用变量分离法研究了(2+1)维NLS方程的局部结构,得到了一系列包含环孤子,呼吸子和瞬子等的局域解[21];李景美,张金良等人通过导出常系数柱(球)非线性Schrödinger方程与变系数非线性Schrödinger方程 (NLS) 的一个相似变换并通过G′/G展开法得到了变系数NLS方程的解[22];高秀丽,额尔敦布和等人通过求变分问题的极值和试探函数法等多个方法的组合得到了Cubic-非线性Schrödinger(CNS)方程的精确解[20]. 这些方法在求解非线性偏微分方程的研究中都逐渐成熟,但是并没有研究此类方程的李对称及相应结构,而在众多方法中,李对称方法因为可以判定方程的行波行为和其广泛适用性得到了广泛关注,本文通过复包络变换和李对称方法讨论了Schrödinger方程的李点对称和约化方程,并通过幂级数方法得到了约化方程的一系列新解,从而对于今后研究此类Schrödinger方程提供了更多的方向.
在本文中,第1部分引进复包络变换,将包含复值函数的Schrödinger方程转化为了实函数方程组,并借助Lie对称方法得到了对应实函数方程组的点对称;第2部分,根据第一部分得到的对称对实函数方程组进行对称约化,得到了部分精确解;第3部分,运用幂级数方法对两类方程的高阶约化方程进行研究,得到了新的精确解.
1 两类Schrödinger方程的复包络变换和李点对称
在包含复函数的非线性偏微分方程的研究中,为了检测方程有没有行波行为,常用的方法就是引入变换将复函数方程转化为实函数方程组,本文中引入复包络变换
u(x,t)=p(x,t)+iq(x,t),
(3)
其中i为虚数单位,将 (3) 代入方程 (1) 得到如下方程组
pt+αp2q+αq3+qxx=0,qt-αq2p-αp3-pxx=0.
(4)
同样将 (3) 式代入方程 (2) 得到对应的实函数方程组
pt+pxxx+12p2px-12q2px-24pqqx=0,qt+qxxx+12p2qx-12q2qx+24pqpx=0.
(5)
设方程组 (4) (5) 的单参数向量场为
(6)
其中ξ(x,t,p,q),τ(x,t,p,q),φ(x,t,p,q)和ψ(x,t,p,q)为向量场中的待定系数函数,如果向量场 (6) 存在方程组 (4) (5) 的对称,向量场需要满足以下条件
pr(i)V(Δ1)|Δ1=0=0,pr(j)V(Δ2)|Δ2=0=0.
(7)
pr(i)V表示向量场的i阶延拓,在方程组 (4) 中Δ1=pt+αp2q+αq3+qxx,Δ2=qt-αq2p-αp3-pxx,方程组 (5) 中Δ1=pt+pxxx+12p2px-12q2px-24pqqx,Δ2=qt+qxxx+12p2qx-12q2qx+24pqpx.
接下来用标准对称分析方法研究两类方程组的向量场.
(I) 方程组 (4)通过无穷小生成元可以得到无穷多个点对称,得到的李点对称为
(8)
其中
不变群的全体生成元V构成了一个五维李代数,并有以下一组基

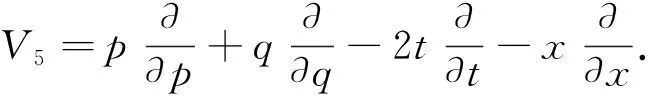
(9)
(II) 方程组(5)得到的李点对称为
(10)
其中
不变群的全体生成元V构成了一个三维李代数,有如下一组基
(11)
通过求得的方程的向量场,可以对非线性方程进行对称约化,从而使偏微分方程转化为常微分方程进行求解,通过向量场也可以对方程的守恒律进行研究.
2 两类非线性方程(组)的约化和精确解
在上一部分我们已经得到了方程 (4)和方程 (5)两类非线性方程组的向量场,在这一部分,将对两类方程组的对称约化及精确解进行研究.
首先考虑方程组 (4)的特殊向量场、约化方程和精确解
p=f(t),q=g(t).
(12)
将不变量 (12) 代入方程 (4) , 得到约化方程
f′+αf2g+αg3=0,g′-αg2f-αf3=0,
(13)
其中f′=df/dξ,g′=dg/dξ.
p=f(x-ct),q=g(x-ct).
(14)
将不变量 (14) 代入方程 (4),得到约化方程
cf′+αf2g+αg3+g″=0,g′-αg2f-αf3-f″=0,
(15)
其中f′=df/dξ,g′=dg/dξ.
-f′ξ-f+2αgf2+2αg3+2g″=0,g′ξ+g+2αg2f+2αf3+2f″=0,
(16)
其中f′=df/dξ,g′=dg/dξ.
接下来根据方程 (5) 的特殊向量场研究非线性方程组 (5) 的约化方程和精确解.
p=f(t),q=g(t).
(17)
将不变量 (17) 代入方程 (5) , 得到约化方程
f′=0,g′=0,
(18)
其中f′=df/dξ,g′=dg/dξ.因此方程组 (5) 有解p=c1,q=c2,其中c1,c2为任意常数,很明显解是无意义的.
p=f(x-ct),q=g(x-ct).
(19)
将不变量 (19) 代入方程组 (5),得到约化方程
-cf′+f‴+12f2f′-12g2f′-24fgg′=0, -cg′+g‴+12f2g′-12g2g′+24ff′g=0,
(20)
其中f′=df/dξ,g′=dg/dξ.
f′ξ+f-3f‴-36f2f′+36g2f′+72fgg′=0,g′ξ+g-3g‴-36f2g′+36g2g′-72ff′g=0,
(21)
其中f′=df/dξ,g′=dg/dξ.
值得注意的是,约化方程 (16) 和 (21) 都是高阶的非线性微分方程,我们将在下一节对这两个方程进行讨论和研究.
3 两类非线性方程组的幂级数解
在第二部分,通过Lie对称分析已经得到了方程(4)和方程(5)两类非线性方程组的对称及约化方程,在本节将对高阶约化方程(16)和(21)进行研究,通过幂级数解得到了含有非恒量系数的幂级数形式解.
设方程组有下列形式的幂级数解
(22)
将式 (22) 代入方程 (16) 得
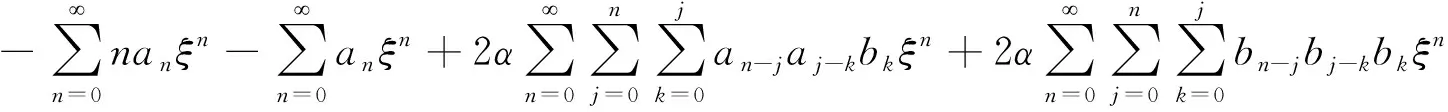
(23a)
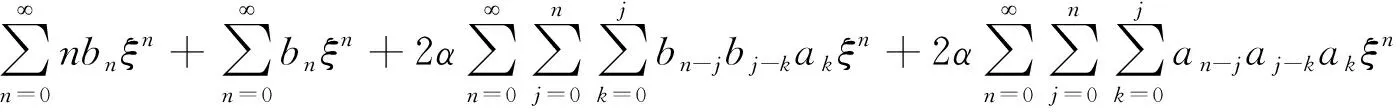
(23b)
比较相同系数项,可得
(24)
其中n=0,1,2,.对于任意选取的常数a0,a1,b0和b1都可以得到
(25)
根据递推公式,an和bn的其余各项都可以通过式(24)得出,这表明方程(16)存在系数为式(24)的幂级数解.则方程(24)有如下形式的幂级数解
(26)
则非线性方程组 (4) 的精确解为
(27)
将 (22) 式代入方程(21) 得
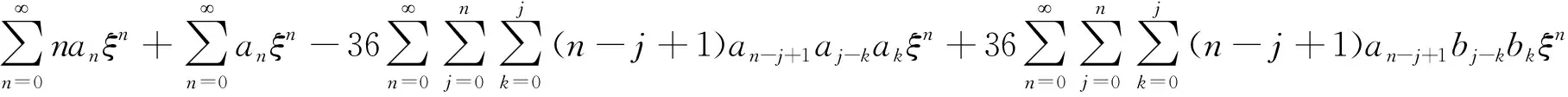
(28)
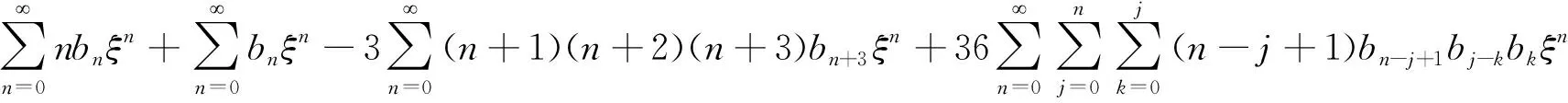
(29)
比较同类项,同理可得an+3和bn+3的表达式
(30)
(31)
其中n=0,1,2,…对于任意选取的常数a0,a1,b0和b1,方程 (21) 存在如下形式的解
(32)
非线性方程(5)的解为
(33)
(34)
本文中应用幂级数方法对方程(16)和(21)两类不同阶的Schrödinger方程复包络变换后的的方程组的精确解进行研究,得到了相应的幂级数解,这表示幂级数方法在求解不同阶的多种非线性方程和非线性方程组中都有其强大的适用性和重要性.在数学物理领域通过得到的幂级数解也可以得到所研究方程的精确解并解释一系列复杂的物理现象,因此该方法在理论和应用上都很方便.
4 结论
本文通过Lie对称分析和幂级数函数法对CNS和NLS两类Schrödinger方程进行研究,通过复包络变换和李对称得到了两类方程的李点对称和约化方程,进而通过约化方程得到了两类方程的高阶约化方程的幂级数解,这些解在数学物理方面有很重要的特征,也证明了李对称方法和幂级数函数方法是研究和求解非线性方程(组)的有效方法.

