裂隙网络非达西渗流REV及非达西系数张量研究

牛玉龙，王 媛，于 可，冯 迪

（1. 河海大学 岩土力学与堤坝工程教育部重点实验室，江苏 南京 210098；2. 中国长江三峡集团公司，北京 100038；3. 河海大学 隧道与城市轨道工程研究所，江苏 南京 210098）

1 研究背景

在采用有限元软件进行工程区渗流模拟时，往往需要确定裂隙岩体的等效渗透系数张量，同时，等效渗透系数张量也是表征裂隙岩体渗流各向异性的重要参数。对于裂隙岩体等效渗透系数张量的确定，就涉及到确定渗流所需的表征单元体积（Representative Elementary Volume，REV）问题。因此，确定裂隙岩体渗流的REV对于研究裂隙岩体的渗流各向异性特性具有重要的意义。

离散裂隙网络模型被广泛应用于裂隙岩体渗流REV及等效渗透系数张量的研究。Long等［1］首先研究了离散裂隙网络进行渗流分析时，多大的尺寸才可被认为是连续介质体。Oda［2-3］通过研究裂隙岩体的渗透张量及其各向异性来对裂隙岩体的REV进行了探讨。Min等［4］根据现场勘察裂隙几何参数服从的分布规律，利用Monte Carlo方法生成了离散裂隙网络，并提出了使用CV值和预测误差作为确定REV的标准。Baghbanan等［5］和Klimczak等［6］研究了裂隙开度与裂隙长度是否存在相关关系情况下的REV，发现考虑相关性确定的裂隙岩体REV和渗透率张量更大。刘日成等［7］分析了不同的开口度分布形式对岩体裂隙网络等效渗透系数方向性以及REV的影响。上述研究都是基于裂隙渗流服从立方定律的裂隙网络达西渗流模型，然后以等效渗透系数作为判断渗流REV的参数，并以此确定裂隙网络的等效渗透系数张量。但随着研究的深入，刘日成等［8-9］、张燕等［10］和尹乾等［11］进行了小尺度（边长最大不超过1 m）的数值或室内试验，发现随着水力梯度的增加，裂隙网络渗流也不再服从达西定律。因此，非达西渗流状态下裂隙网络的渗透特性不能再单以等效渗透系数进行表征，进而非达西渗流状态下裂隙网络的渗流REV亦不能再单以等效渗透系数进行确定。

对于裂隙岩体非达西渗流状态下水力特性的研究，基于单裂隙立方定律的传统离散裂隙网络模型亦不再适用。因此，研究学者们开始改进传统离散裂隙网络模型，用以研究裂隙网络非达西渗流特性。柴军瑞［12］和徐维生等［13-14］将单裂隙立方定律替换为单裂隙非达西渗流指数型公式，熊祥斌［15］和刘日成等［16］将单裂隙立方定律中等效水力隙宽替换为了关于水力梯度的函数，继而构成了离散裂隙网络的非线性渗流方程组，再通过迭代法求解，从而实现了对裂隙网络非达西渗流的计算模拟。同时，熊祥斌［15］和刘日成等［16］研究发现，在相同水力梯度条件下，考虑惯性效应（即非达西渗流）的裂隙网络等效渗透系数会比不考虑时的偏小。但是，非达西渗流是非线性渗流，不同水力梯度下的惯性效应亦不相同，这意味着不同的水力梯度对应不同的等效渗透系数张量。对于存在高水力梯度的大坝或深埋隧洞等工程，整个工程区的水力梯度差异性较大，只采用等效渗透系数张量明显无法较好地模拟出整个工程区渗流场情况。因此，需要引进新系数张量来反映等效渗透系数张量随水力梯度变化的特性，同时，需要利用改进的离散裂隙网络模型对新系数张量进行研究。

本文采用可以反映裂隙岩体非达西渗流各向异性的Forchheimer定律为理论基础，进而引入等效非达西系数张量用于反映等效渗透系数张量随水力梯度变化的特性，从而裂隙岩体非达西渗流特性将由等效渗透系数张量与等效非达西系数张量两个张量共同表征。为研究确定两个张量之间的关系及其分别确定的REV是否存在差异性，本文采用改进线素法模型模拟离散裂隙网络模型的非达西渗流，确定裂隙岩体的非达西渗流REV与等效非达西系数张量，以期为后续模拟工程区非达西渗流场所需有效计算参数和合理计算范围提供参考依据。

2 理论背景

2.1 单裂隙运动方程 对于单裂隙渗流往往将裂隙简化为两个光滑平行板构成的裂隙，从而建立了立方定律［17］：

式中：q为单裂隙的流量；∇P 为压力梯度；w为垂直于流动方向的裂缝宽度；bh为等效水力隙宽；μ为黏度。

随着压力梯度的增加，裂隙中流速的增加，裂隙中流体流动的惯性效应愈加明显，进而导致压力梯度∇P 与流量q之间不再严格为线性关系时，立方定律无法再用于定量描述这种非线性关系。研究学者们建立了很多非线性渗流方程，其中Forchheimer方程由于具有较为明确的物理意义［18］，而被广泛采用。本文亦采用Forchheimer方程：

式中：a、c 分别为黏滞力项和惯性力项系数。对于单裂隙而言，系数a 与c 可以分别通过下式得到［19］：

式中：k为裂隙的渗透率；β为非达西系数；ρ为水的密度；Dh为裂隙的等效过流横截面。

从式（3）的定义来看，当裂隙中的流速足够小时，非线性项cq2远小于线性项aq，则式（2）可以简化为式（1），线性项a值代表了达西渗透系数的倒数，可以用来描述裂隙达西渗流的情况，与立方定律形式一致。

2.2 裂隙网络渗透张量 裂隙岩体中的裂隙常成组分布，每组裂隙有较为稳定的产状，使得裂隙岩体的渗透性具有明显的各向异性，如果将裂隙介质的透水性平均到整个岩体，就可以将整个岩体等效成各向异性的渗透介质。对于各向异性介质，达西定律可表示为：

式中：uj为j方向的流速；Qj为j方向的流量；A为过流横截面面积；Ji为i方向的水力梯度；P，i为i方向的压力梯度；g为重力加速度；Kji为等效渗透系数张量，记做K。

由于本文研究的是二维平面裂隙网络，不需要考虑位置水头的影响，只须考虑压力水头的影响，因此，本文中水力梯度能与压力梯度进行直接换算。对于裂隙网络而言，当水力梯度（压力梯度）大于一定值时，流速与水力梯度（压力梯度）的比值也不再为常量，也就不再满足达西定律，裂隙网络中的渗流也就进入了非达西渗流状态，同样可以采用Forchheimer 定律来描述这种非线性关系。对于渗流各向异性介质的Forchheimer定律［20］可表示为：

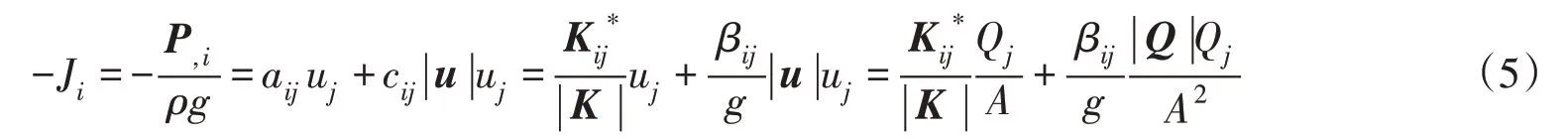
式中：aij、cij分别为黏滞力项与惯性力项系数张量；Kij为渗透系数张量；βij为非达西系数张量；u为流速矢量；Q 为对应流速矢量u的流量； |u |为流速的模； |Q |为流量的模；为等效渗透系数矩阵的逆矩阵，记做K-1；βij为等效非达西系数张量，记做β。

从式（5）可以看出，某一水力梯度（压力梯度）的分量不仅与流速（流量）相应分量成二次多项式关系，而且还与流速（流量）其他方向的分量也成二次多项式关系。对于裂隙网络采用等效连续介质实现非达西渗流的模拟，不仅需要求得裂隙网络的等效渗透系数张量K，还需要求得裂隙网络的等效非达西系数张量β。等效渗透系数张量与等效非达西系数张量将是等效连续介质非达西渗流模型中最为重要的参数。

3 线素法模型求解非达西渗流

线素法模型的基本理论与推导过程详见文献［21］，这里重点阐述线素法模型求解非达西渗流的方法。对任一个二维裂隙网络而言，都可以假设成其由N个裂隙节点和M个线元组成，且设任一线元j对应一个裂隙隙宽为aj且线长为lj的裂隙段。整个裂隙网络的节点水头与节点流量可以用下式表示：

式中：E 为裂隙网络的N×M 阶衔接矩阵；Tl 为1×M 阶线元水力传导矩阵；H 为N×1 阶节点水头向量；G为N×1阶节点源项，表示N×1阶节点的净流量。

根据裂隙网络施加的边界，将边界条件代入式（6），就可以得到相应边界上的水头或者流量，这便是基于单裂隙立方定律的线素法模型求解裂隙网络达西渗流的过程。当水力梯度大于某一个值时，裂隙中流体不再符合立方定律，这里采用Forchheimer方程对于裂隙非达西渗流进行描述，则任一个线元j的流量与水力梯度可被写为：

式中：aj、cj分别为线元j非达西渗流的一次项与二次项系数；hj为线元j的深度，hj=1 m；qj为线元j的流量；∆Hj为线元j 的水头差；βj为线元j 的非达西系数。求解上面的一元二次方程，由于流量为正，所以线元j的流量为：

由式（8）可知，Tlj是线元j水头差∆Hj的函数，将其代入式（6），则形成了整个裂隙网络的非达西渗流方程组。由于Tlj与水头有关，则式（6）构成的非达西渗流方程组为非线性方程组，需要采用迭代法进行求解。这里采用以下的迭代运算步骤进行求解：（1）给定各线元的初始水头差∆H0=0，则初始的Tl0为达西状态下的Tl，代入式（6），求解得到各节点的水头H1；（2）第1次迭代，将求得的各节点水头H1，可以得到各线元的水头差∆H1，进而将其代入式（8），可得到各线元的Tl1，再代入式（6），求解得到各节点的水头H2；（3）第n次迭代，求得的各节点水头Hn（n=2，3…），可以得到各线元的水头差∆Hn，进而将其代入式（8），可得到各线元的Tln，再代入式（6），求解得到各节点的水头Hn+1；（4）将max（Hn+1-Hn）＜max（H）×10-5m 作为非线性方程组迭代的收敛标准，当满足标准时，输出G，若不满足，继续进行迭代。

4 非达西渗流REV与非达西系数张量

4.1 裂隙网络的构建 本次采用的裂隙网络的几何参数是在Min等［4］和Baghbanan等［22］文中采用是英格兰Cambria 郡Sellafield地区一个位点特征的地质调查结果。表1给出了裂隙网络几何参数的相关信息，包括4个裂缝组，裂缝的方向遵循Fisher分布规律，基于这些参数采用Monte Carlo法生成一个离散裂隙网络模型，进而确定此裂隙网络的等效渗透系数张量与等效非达西系数张量。

表1 生成离散裂缝网络（DFN）的裂隙参数

通过上述参数生成了一个300 m×300 m的大范围的裂隙网络作为研究渗透张量相关性质的二维裂隙网络，由于裂隙的平均迹线长为0.92 m，所以此裂隙网络的渗流REV不会很大，因此为了减少计算量，从中截取了一个20 m×20 m范围的裂隙网络作为分析对象，如图1（a）所示。

对于一个给定的裂隙网络，首先需要研究其是否可以存在REV，并在确定REV的基础上得到此裂隙网络的等效渗透张量。为此，以该分析域的中心点为基准点，将分别截取边长从1 m到10 m的正方形计算区域，如图1（a）所示。为了进一步判断在某一边长时等效渗透系数以及等效非达西系数是否能形成渗透张量，将分析边框按间隔为30°顺时针旋转截取出计算模型，直至旋转360°，共可截取12个边长一致的裂隙网络计算模型，图1（b）为分析范围边长为10m时裂隙网络的计算工况及计算模型。结合不同边长与不同角度，对于此裂隙网络共需120个计算模型。

4.2 达西渗流下的REV及等效渗透系数张量 对于达西渗流而言，对旋转裂隙网络模型进行方向等效渗透系数计算的数值实验，可验证计算得到相关区域的等效方向渗透系数是否可近似表示为张量。如果裂隙网络模型的等效渗透系数具有张量性质，则压力梯度方向上的方向等效渗透系数椭圆便可拟合得到。

图1 确定裂隙网络渗透性REV的计算方法

本文首先进行裂隙网路的达西渗流模拟，为确定某一计算模型的等效渗透系数张量，需要对计算模型的4个边界施加不同的水压边界。这里设沿计算角度的方向设定为x轴，垂直x轴并逆时针旋转的为y轴，图2示意了计算边长为5 m、计算角度为0o时计算模型沿x、y方向压力梯度分布的边界条件，沿x方向压力梯度分布时，在左、右边界施加固定水压边界，上、下边界施加由左右边界水压确定的线性水压边界；沿y方向压力梯度分布时，则左右边界与上下边界的设定互换（水压值不变）。根据线素法建立的式（6）结合上述水压边界可以计算得到4条边界上每条边界的净流量，然后将左、右边界净流量的平均值作为x方向的流量，将上、下边界净流量的平均值作为y方向的流量，如下式：

式中：Qx、Qy分别为x、y方向的流量；Qx1、Qx2分别为左、右边界的净流量；Qy1、Qy2分别为上、下边界的净流量。

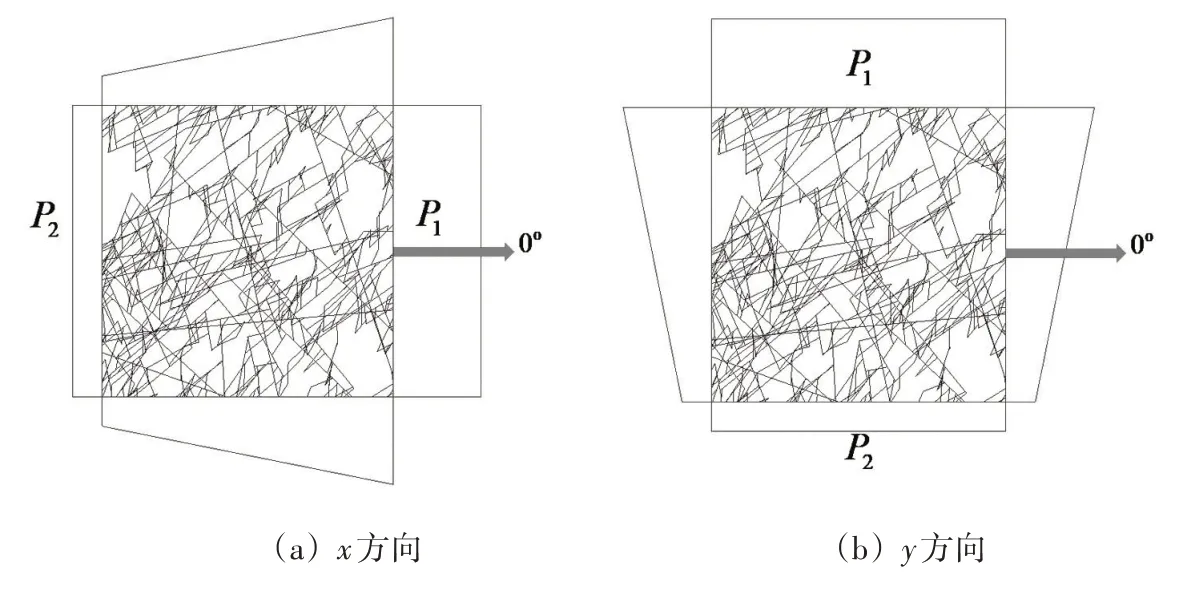
图2 裂隙网络计算模型的边界条件

根据达西定律公式，结合裂隙网络计算模型的边界条件可以计算出裂隙网络的等效渗透系数张量的各个分量Kxx、Kyy、Kxy和Kyx。根据沿x、y方向的压力梯度分布的边界条件，可建立两个方程组：

将计算出的某一边长下各个方向上1 Kxx的点绘制于极坐标中，以各个方向1 Kxx是否能够近似构成椭圆，来判断裂隙网络在某一边长时是否存在渗透张量及此分析区域的裂隙网络是否可以等效为连续介质渗透模型。为了进一步确定裂隙网络REV的大小，这里采用回归分析的相关系数R2作为判定裂隙网络REV大小的参数，根据图3显示，随着分析区域边长的增大，相关系数R2也逐渐增大，在边长为6 m时，R2已经大于0.9，此后，R2不再随分析区域边长增大而增大而是趋于稳定，因此可认为对于此裂隙网络而言，边长为6 m时已经具有将裂隙网络渗透性等效为连续介质渗透模型的基础，因此根据相关系数R2确定的REV为6 m。对应的渗透系数张量为：

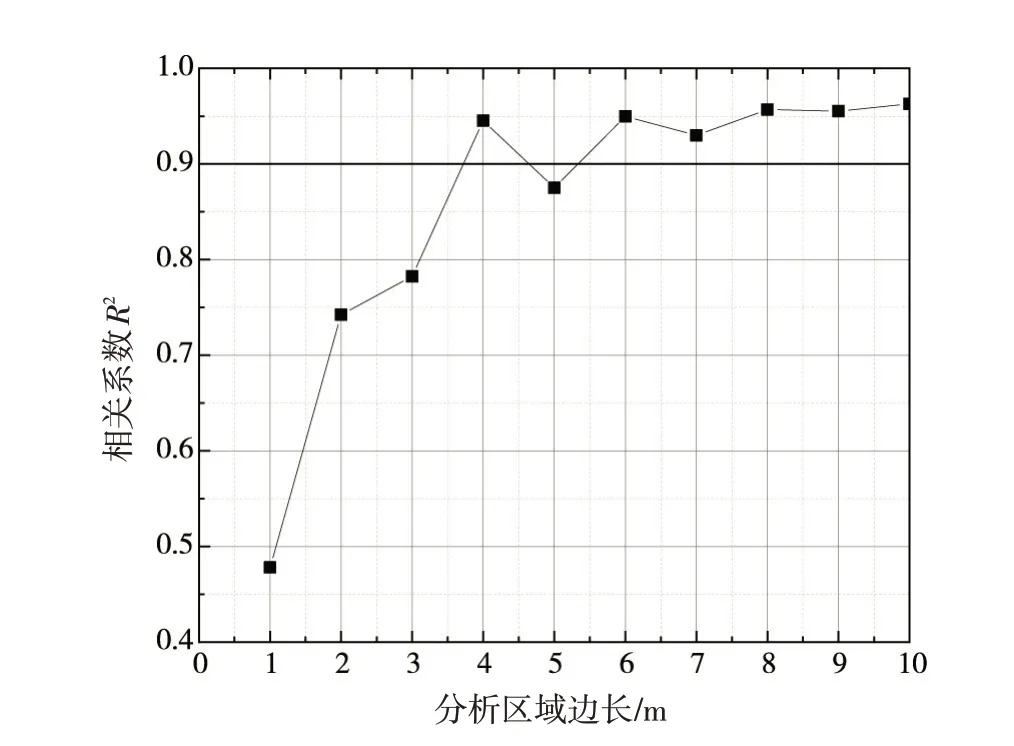
图3 等效渗透系数拟合渗透椭圆的相关系数R2随分析区域边长的变化曲线

进一步通过等效渗透系数张量可以确定其渗透椭圆的主方向为18.13o。图4分别给出了分析区域边长在1、3和6 m时的等效渗透系数椭圆，从图4可以看出此裂隙网络具有渗流各向异性，且在6 m时已具有很好的张量性。

图4 不同边长下等效渗透系数的渗透椭圆

4.3 非达西渗流下的REV及等效非达西系数张量 根据式（8）可知，模拟裂隙网络的非达西渗流在知道每条裂隙的水力隙宽a的同时也应确定每条裂隙的非达西系数β，秦峰等［23］试验研究结果显示，光滑平行板模型的非达西系数跟隙宽相关。根据表1可知，裂隙网络中裂隙的平均隙宽为65 μm，为较为准确的确定隙宽为65 μm 时光滑平行板模型的非达西系数β，这里采用Fluent［24］进行计算模拟，计算出不同压力梯度下的流量。根据达西定律可以计算出不同压力梯度下的等效渗透系数如图5（a）所示。从图5（a）可见，在压力梯度大于1 kPa/m（即水力梯度为0.1）时，渗透系数开始明显偏离立方定律。从水力梯度与裂隙平均流速之间的关系（如图5（b））也显示，在低水力梯度时，流速与立方定律一致，随后随着水力梯度的增加，流速逐渐偏离立方定律。采用式（2）与式（3）拟合得到隙宽65 μm光滑平行板模型的非达西系数β=679.2m-1。

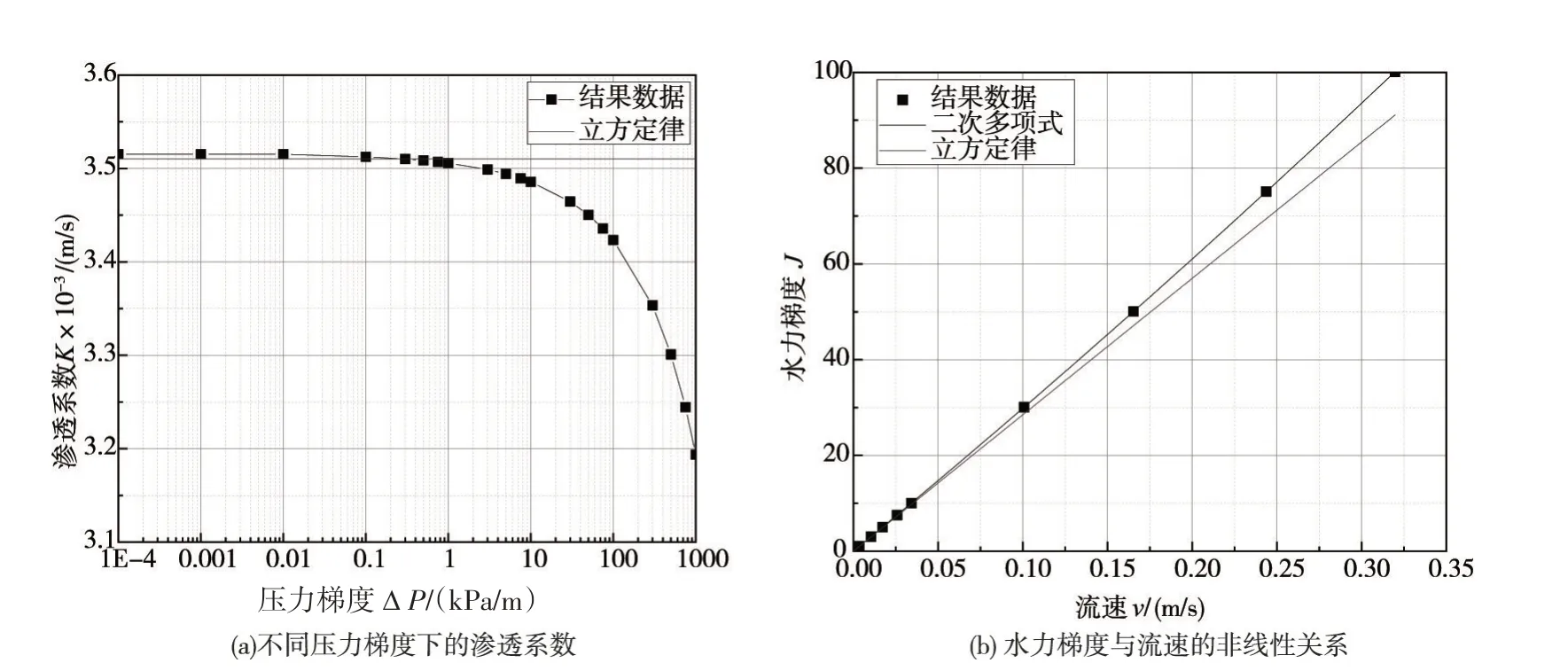
图5 隙宽为65μm时光滑平板模型的数值模拟结果

对于非达西渗流而言，对旋转裂隙网络模型进行方向非达西渗流计算的数值实验，可验证Forchheimer方程计算得到不同分析范围的等效方向渗透系数与等效方向非达西系数两个张量是否稳定。如果裂隙网络模型的等效渗透系数与等效方向非达西系数的两个张量稳定，则压力梯度方向上的等效方向渗透系数椭圆与等效方向非达西系数椭圆便皆可拟合得到。

对于裂隙网络非达西渗流模拟求等效渗透系数张量与等效非达西系数张量，与裂隙网络达西渗流模拟需要采用的边界条件设置方法一致（如图2），根据沿x，y方向的压力梯度分布的边界条件，可建立两个Forchheimer方程组：

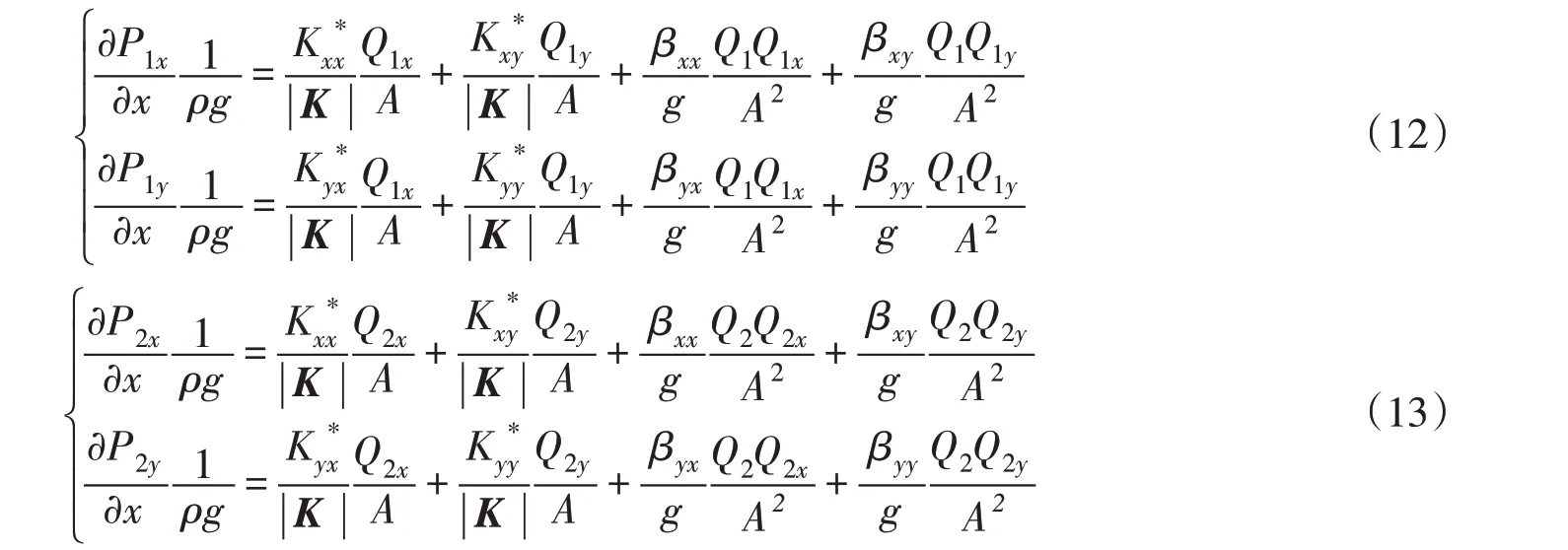
在1个压力梯度下也可以得到4个方程，但与达西渗流不同是非达西渗流方程组不仅存在等效渗透系数张量K4 个系数，而且存在等效非达西系数β 张量4 个系数，这样就形成了1 个欠定线性方程组。本文通过模拟9个不同压力梯度（水力梯度）情况下的渗流情况，这里选用的9个水力梯度依次为0.001、0.01、0.1、1、10、30、50、75、100，就可以建立4×9个线性方程，进而形成了1个超定线性方程组，然后采用最小二乘法求解超定线性方程组，从而求得某一分析边长某一角度计算模型的等效渗透系数张量K和等效非达西系数张量β。

将非达西渗流计算结果求得的等效渗透系数张量，采用与达西渗流计算结果求出的等效渗透系数张量采用相同方法拟合渗透椭圆，即将某一边长下各个方向上Forchheimer方程求得1 Kxx的点绘制于极坐标中，如果拟合的椭圆与达西渗流时的椭圆具有一致性，说明非达西渗流计算亦可准确求得等效渗透系数张量。将不同分析区域边长下达西与非达西渗流计算结果拟合得到主渗透系数与主方向角度列于表2，从表2 可见，达西与非达西渗流拟合出主渗透系数K1与K2的误差皆在0.04%之内，主方向角度α 的误差除边长为1 m 时的误差在0.255%，其余边长下的误差都在0.02%之内。因此，Forchheimer方程计算结果求得的等效渗透系数张量具有较高的精度，即采用Forchheimer方程也可以求得的达西渗流时的等效渗透系数张量。

表2 达西与非达西渗流拟合等效主渗透系数结果

图6 等效非达西系数拟合渗透椭圆的相关系数R2随分析区域边长的变化曲线

为了进一步确定裂隙网络在非达西渗流状态下REV的大小，本文采用等效非达西系数回归分析的相关系数R2作为判定裂隙网络REV大小的参数。根据图6显示，随着分析区域边长的增大，相关系数R2也整体趋势逐渐增大，在边长为8 m 时，R2已经大于0.9，且此后R2基本趋于稳定。但是图3与图6里的R2在到达稳定值之前都存在一定的波动情况，这主要是由于在到达REV之前等效渗透系数会围绕一个稳定值波动［25］，进而导致了采用等效渗透系数拟合的系数R2产生波动。因此可认为，对于此裂隙网络而言，边长为8 m时已经具有将裂隙网络非达西渗透性等效为可用于非达西渗流计算的连续介质渗透模型的基础，因此根据相关系数R2确定的REV 为8 m。对应边长下的等效非达西系数张量为：

图7 不同边长下等效非达西系数的渗透椭圆

进一步通过等效非达西张量可以确定其渗透椭圆的主方向为16.55°。图7分别给出了分析区域边长在2、5和8 m时的等效非达西系数椭圆。从图7也可以看出，此裂隙网络等效非达西系数具有各向异性，在边长为8 m时拟合椭圆基本稳定，等效非达西系数已具有很好的张量性。这说明此裂隙网络在非达西渗流状态下也存在REV，非达西渗流特性可用等效非达西系数较好的表示。从等效渗透系数张量与等效非达西系数张量的主方向可知，两者基本一致。但是从渗透椭圆的形状来看，等效渗透系数椭圆的长轴与等效非达西系数椭圆的长轴之间的夹角为90°，可定性的反映出等效渗透系数越小，等效非达西系数越大，这与许凯等［26］、Li等［27］和Takhanov［28］总结的等效非达西系数与等效渗透系数的次幂呈反比例的公式反映的规律相一致。

4.4 非达西系数张量确定REV的讨论 采用英格兰Sellafield地区实测裂隙数据生成了一个裂隙网络，对其进行达西渗流计算与非达西渗流计算，采用等效渗透系数拟合渗透椭圆的相关系数R2大于0.9时，确定的裂隙网络REV为6 m；采用等效非达西系数拟合渗透椭圆的相关系数R2大于0.9时，确定的裂隙网络REV为8 m。反映出对于同一裂隙网络而言，采用等效连续介质模型模拟非达西渗流需要确定渗透参数的REV要比模拟达西渗流需要确定渗透参数的REV要大。由于裂隙岩体非达西渗流广泛存在，确定非达西渗流状态下裂隙网络的REV及等效非达西系数张量具有更为重要的工程意义与科学价值。

因国内外关于裂隙网络非达西渗流状态下REV的研究较少，所以关于裂隙网络等效渗透系数与等效非达西系数确定的REV不一致性的原因也还处于探索研究阶段，但开展了一些关于确定渗透介质非达西系数β的研究，也建立了不同的非达西系数β计算公式，这些公式表明β不仅与渗透率k有关，还与其他介质参数相关。如Macdonald等［29］、Evan等［30］、Geertsma［31］发现其还与多孔介质的有效孔隙率ϕ有关；Knupp等［32］指出β还与惯性系数CF有关，其中CF代表了固体多孔基质施加的微观形式阻力，它取决于每个代表性体积内固体的几何形状；Li等［27］和Veyskarami等［33］提出β与许多裂隙岩体的物理参数（特别是ϕ、k和曲折度τ）有关。由此可知，渗透介质的非达西系数β要比渗透率k反映出的介质的物理参数更为丰富，进而可导致等效非达西系数稳定所需要的REV要比等效渗透系数确定的REV更大。

5 结论

裂隙网络非达西渗流研究中的单裂隙不再符合立方定律，成为了非线性渗流，根据改进线素法及Forchheimer定律可以计算得到与线素法及达西定律一致的等效渗透系数张量。等效非达西系数张量确定的渗流REV要比等效渗透系数张量确定的渗流REV要大。根据等效渗透系数的渗透椭圆与等效非达西系数的渗透椭圆可知，对于同一裂隙网络，等效渗透系数张量与等效非达西系数张量的主轴方向是一致的，但是两者的长轴互相垂直。

本文首次采用包含等效非达西系数张量的Forchheimer 方程对裂隙网络非达西渗流特性进行研究，只研究了一个固定隙宽的裂隙网络，旨在为定量研究裂隙网络非达西渗流的水力特性提供一种新的思路与方法。本文没有对裂隙隙宽随机变化的情况进行研究，而裂隙隙宽变化对于等效非达西系数张量及其确定REV的影响还需要进一步探讨研究。