航标运行状态模式识别和数值预测

陈麒龙 陆一军

摘 要：针对航标运行状态模式识别依赖经验阈值的现状，为检验经验阈值是否具有普适性，提出基于概率的阈值模式识别效率度量算法。实验结果表明：该算法能准确度量阈值的模式识别效率;经检验，经验阈值不具备普适性。因而，提出基于概率的模式识别模型。实验结果表明：以概率作为阈值具有普适性，该模型能准确识别频繁模式和异常模式，且性能更好。为实现数值预测，提出基于概率密度的加权平均算法。实验结果表明：该算法的预测精度较高。本文为航标运行状态模式识别和数值预测提出了新的解决方案。

关键词：水路运输;航标;概率;模式识别;数值预测

航标遥测数据是反映航标运行状态的数值信息，包括：数据采集时间（Time）、电压（Voltage）、电流（Current）、航标位置（Longitude、Latitude）、离位距离（Distance）。频繁模式表示航标的“常态”，异常模式表示航标的“非常态”。对频繁模式和异常模式的识别，传统方法是依据经验阈值进行分类，存在主观臆断的问题。对航标运行状态的数值预测，目前仍处于研究阶段。如何检验经验阈值是否具有普适性，如何实现航标运行状态的数值预测，是亟待解决的问题。

对数据的频繁模式和异常模式的模式识别，已有不少算法和模型，如：基于相关性度量算法、基于频繁子树算法、基于最大熵隐马尔科夫模型，以及基于统计特征的支持向量机 [1-4]。移动对象位置预测的模型有：马尔科夫模型、高斯混合模型、卷积神经网络模型[5-7]。核密度估计（kernel density estimation，KDE）是一种估计数据的概率密度函数（probability density function，PDF）的算法，利用概率密度函数可以计算出给定数值区间的概率。概率可以用来度量经验阈值的模式识别效率，以此来检验经验阈值是否有效，判定经验阈值是否具有普适性。概率反映随机事件发生的可能性，是客观的，以概率作为阈值进行分类，就是将“大概率”的数据作为“常态”，将“小概率”的数据作为“非常态”，从而使阈值成为一种客观的指标，而具有普适性。概率密度与概率是正相关的，将概率密度转化为权重，以加权平均数作为预测值，既消减了极端值的影响，又使预测值趋于“大概率”。相对于相关性度量算法、频繁子树算法、马尔科夫模型、支持向量机、高斯混合模型、卷积神经网络模型等，核密度估计和概率的计算过程更为简单，算法和模型易于解释，且性能良好，适合航标运行状态模式识别和数值预测。

1 经验阈值检验

1.1核密度估计原理

1.2 实例分析

已知经验阈值：电压10.8 V，电流0.09 A，离位距离150 m。以洋山港主航道的Y4#灯浮标连续60天凌晨3时的航标遥测数据为例（如表1），检验经验阈值是否有效，是否具有普适性。

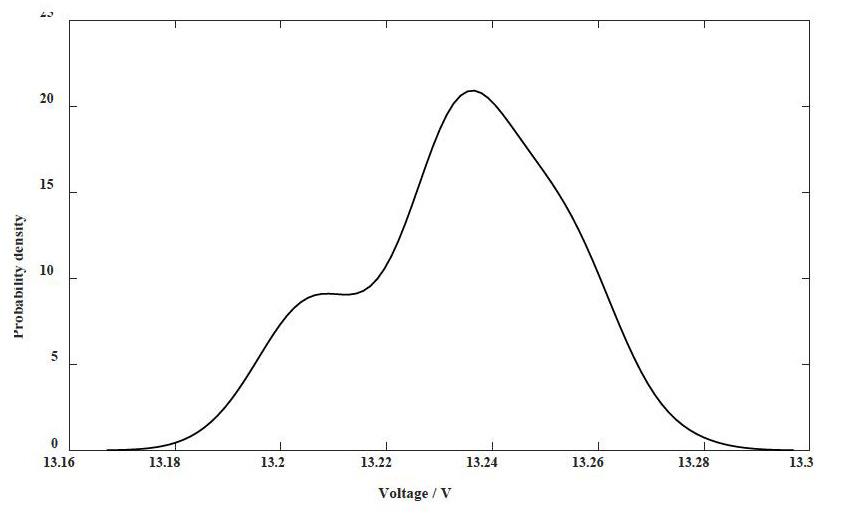
电压的概率密度分布如图1所示。对电压经验阈值构造区间为（0，10.8]，计算出电压小于或等于10.8 V的概率为0，表明在凌晨3时，以“10.8 V”作为电压阈值无法有效识别异常模式，应当增大阈值。当阈值为“13.2 V”时，区间（0，13.2]的概率为0.0651，表明在该时段，以“13.2 V”作为阈值识别异常模式的效率为6.51%，识别频繁模式的效率为93.49%。

电流的概率密度分布如图2所示。对电流经验阈值构造区间为[0，0.09]，计算出电流小于或等于0.09 A的概率为0.0506，表明在凌晨3时，以“0.09 A”作为电流阈值，识别异常模式的效率为5.06%，识别频繁模式的效率为94.94%，电流经验阈值有效。

离位距离的概率密度分布如图3所示。对离位距离经验阈值构造区间为[150，+∞），计算出离位距离大于或等于150 m的概率为0，表明在凌晨3时，以“150 m”作为离位距离阈值，无法有效识别异常模式，应当减小阈值。当阈值为“75 m”时，区间[75，+∞）的概率为0.0436， 表明在该时段，以“75 m”作为阈值识别异常模式的效率为4.36%，识别频繁模式的效率為95.64%。

以上实验表明：

（1）概率可以准确度量阈值的模式识别效率，可以用来检验经验阈值是否有效;

（2）经验阈值不具有普适性;

（3）利用概率可以找到合适的阈值。

2 模式识别

2.1 基于概率的模式识别原理

基于概率的模式识别的思路是：以理论概率作为阈值，将概率小于理论概率的样本单元作为异常模式，而概率大于理论概率的样本单元作为频繁模式。模式识别流程是：第一步，对样本容量为n的样本估计概率密度函数;第二步，以新观测值为中心构造区间;第三步，积分计算区间的概率;第四步，计算理论概率作为阈值，将区间的概率与阈值进行比较和分类。

区间长度应当根据样本数据精度来设置，假设新观测值为xi，样本数据的精度为b，那么区间为：[xi-（b/2） ， xi+（b/2）]。阈值a的计算公式为：a=b/R，R表示样本数据的极差，即：R=max（x）- min（x）。阈值的本质是：将样本的值域等间隔划分为m个区间，区间长度为b，样本单元落入某一区间的理论概率，即：m=R/b，a=1/m=b/R。

2.2实例分析

以洋山港主航道Y4#灯浮标“12/31 3：08”的航标遥测数据为例（电压13.228 V，电流0.098 A，离位距离43.6 m）。

电压的数据精度为0.001，样本数据的极差为0.08。因此，阈值为0.0125。新观测值13.228的区间为[13.2275，13.2285]，区间的概率为0.0171，大于阈值，为频繁模式。

电流的数据精度为0.001，样本数据的极差为0.08。因此，阈值为0.0125。新观测值0.098的区间为[0.0975， 0.0985]，区间的概率为0.0860，大于阈值，为频繁模式。

离位距离的数据精度为0.1，样本数据的极差为63.2。因此，阈值为0.0016。新观测值43.6的区间为[43.55， 43.65]，区间的概率为0.0013，小于阈值，为异常模式。

以上实验可以得出结论：

（1）以概率作为阈值，使阈值成为一种客观的指标，具备普适性;

（2）基于概率的模式识别模型能够有效识别频繁模式和异常模式。

2.3 与传统方法比较

传统方法的优点是：直接进行数值对比，计算量小。缺点是：①阈值不具备普适性，如果阈值设置不合理就无法识别异常模式;②阈值设置过程繁琐，为保证阈值有效，需要先度量阈值的模式识别效率，找出合适的阈值;③当灯器设备的规格型号改变时，就必须重新设置电压和电流的阈值;④阈值的模式识别效率需要定期评估，需要定期调整阈值。

新模型的优点是：①以概率作为阈值，具有普适性;②阈值设置简单、灵活可控，可以使用理论概率，也可以使用其他概率;③灯器的型号规格改变时，无需重新设置电压和电流的阈值;④模型易于解释，阈值就是模式识别的效率，对于给定的观测值，阈值越小，分类结果越偏向频繁模式，阈值越大，分类结果越偏向异常模式。缺点是：需要计算概率密度函数和概率，比传统方法的计算量大。

综上所述，新模型的性能比传统方法更好，但是计算量更大。 在航标管理上，总是希望发现航标潜在的异常，而且现在的服务器性能完全能够满足新模型的计算需求。因此，推荐使用新模型。

3 数值预测

3.1基于概率密度的加权平均算法

3.2 实例分析

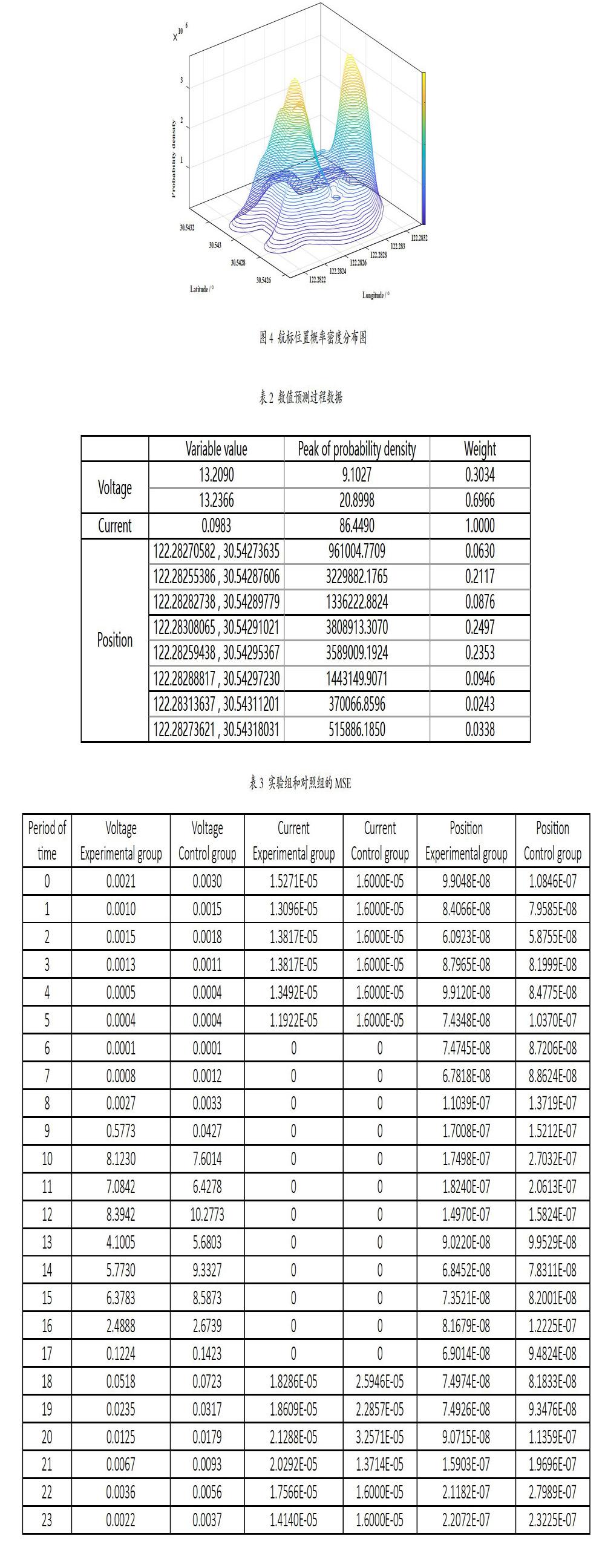
已知“12月31日凌晨3时”的实测数据：电压13.228 V、电流0.098 A、航标位置（122.28244440 °， 30.54266667 °）。以表1的数据为样本，计算“12月31日凌晨3时”的预测值及误差，过程数据如表2所示。

电压的概率密度是双峰分布（如图1），预测值为13.2282，误差为0.0002;电流的概率密度是单峰分布（如图2），因此权重为1，预测值为0.0983，误差为0.0003;航标位置的概率密度是多峰分布（如图4），分别对经度和纬度计算加权平均数，预测值为（122.28278039 °，30.54292107 °），以欧氏距离表示的误差为0.00042。

3.3 数值预测精度评估

以洋山港主航道Y4#灯浮标12月1日至12月7日各时段的数值预测为例。实验组：新算法，对照组：中位数。度量指标：均方误差，                            ，xi是预测值，yi是实测值。如表3所示，各时段的实验组MSE都比较小，表明新算法的预测精度较高;从各时段的MSE看，大多数时段的实验组比对照组小，且MSE之和，实验组也比对照组小，表明新算法的预测精度优于中位数。

3.4统计性质分析

样本数据的特性对预测精度的影响体现在：样本数据的方差越小，则MSE越小;反之，样本数据的方差越大，则MSE越大。将概率密度峰值转化为权重，以加权平均数作为预测值，消减了极端值的影响，使预测值趋于“大概率”。概率密度峰值反映的是“常态”情况下的数值水平，未来偶然出现的“非常态”的实测值，将导致短期内的MSE变大，但是对长期的MSE影响不大。

4 结论

针对航标运行状态模式识别依赖经验阈值的现状，为检验经验阈值的普适性，提出基于概率的阈值模式识别效率度量算法，并用于检验经验阈值。经检验，经验阈值不具备普适性。因而，提出基于概率的模式识别模型，该模型能够有效识别频繁模式和异常模式，而且比传统方法的性能更好。为实现数值预测，提出基于概率密度的加权平均算法，该算法的数值预测精度较高。本文为航标运行状态模式识别和数值预测提供了新的解决方案。下一步，将研究航标漂移、灯器设备故障导致的“持续非常态”情况下的航标运行状态数值预测，拟从短期观测数据着手，分析数值变化趋势，比较和分析线性回归模型、非线性回归模型、时间序列模型的拟合效果和预测精度，寻找合适的模型。

参考文献：

[1] 任永功， 高鹏， 张志鹏. 一种利用相关性度量的不确定数据频繁模式挖掘[J]. 小型微型计算机系统， 2019， 40（03）：623-627.

[2] 吉小洪， 徐爱萍. 基于TrieMerging机制数据流滑动窗口模型的频繁模式挖掘[J/OL]. 计算机应用研究：1-7[2020-02-20]. https：//doi.org/10.19734/j.issn.1001-3695.2019.01.0006.

[3] 胡江， 赵冬梅， 张旭， 等. 基于最大熵隐马尔科夫模型的電网故障诊断方法[J]. 电网技术， 2019， 43（09）：3368-3375.

[4] 刘玉敏， 刘莉. 基于统计特征的动态过程质量异常模式识别[J]. 统计与决策， 2017（19）：32-36.

[5] 宋路杰， 孟凡荣， 袁冠. 基于Markov模型与轨迹相似度的移动对象位置预测算法[J]. 计算机应用， 2016， 36（01）：39-43+65.

[6] 乔少杰， 金琨， 韩楠， 等. 一种基于高斯混合模型的轨迹预测算法[J]. 软件学报， 2015， 26（05）：1048-1063.

[7] 肖延辉， 王欣， 冯文刚， 等. 基于长短记忆型卷积神经网络的犯罪地理位置预测方法[J]. 数据分析与知识发现， 2018， 2（10）：15-20.

[8] 关绍云， 郑丽坤， 金一宁， 等. 基于高斯核函数的局部离群点检测算法[J]. 哈尔滨商业大学学报（自然科学版）， 2019， 35（02）：185-190+203.

[9] Andrew Harvey， Vitaliy Oryshchenko. Kernel density estimation for time series data[J]. International Journal of Forecasting， 2012， 28（01）：3-14.

[10] Moses Charikar， Paris Siminelakis. Hashing-Based-Estimators for Kernel Density in High Dimensions[C]// 2017 IEEE 58th Annual Symposium on Foundations of Computer Science （FOCS）. IEEE， 2017.

[11] 马梦知， 范厚明， 黄莒森， 等. 基于非参数核密度估计的集装箱码头交通需求预测模型[J]. 大连海事大学学报（自然科学版）， 2019， 45（01）：77-84.

[12] 程媛， 迟荣华， 黄少滨， 等. 基于非参数密度估计的不确定轨迹预测方法[J]. 自动化学报， 2019， 45（04）：153-164.