蝴蝶定理对合对应关系的统一形式及其应用

赵临龙， 朱亮卫， 于 婷

（1.安康学院数学与统计学院，陕西安康 725000； 2.陕西理工大学数学与计算机科学学院，陕西汉中 723000）

1 问题背景

2018 年，张峻铭、刘利益在《蝴蝶定理的一个推广》［1］中，给出蝴蝶定理的推广结论.

命题1（蝴蝶定理） 如图1，过圆的弦EF中点P引两弦AD、BC，连接AB、CD分别交EF于X、Y，则PX=PY.

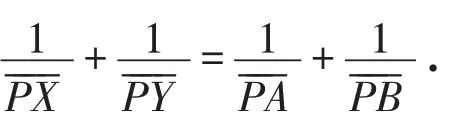
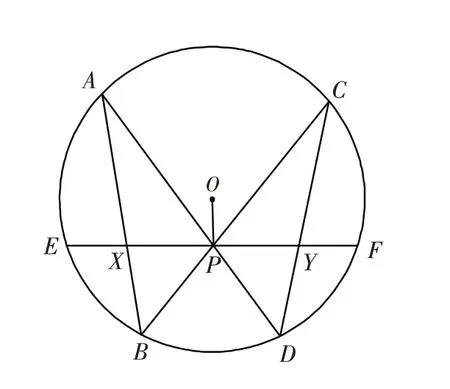
图1 蝴蝶定理Fig.1 Butterfly theorem

命题3（Klamkin 蝴蝶定理） 过圆的弦EF任意点P，取EF上关于P的两个对称点M、N，分别过M、N作两弦AD、BC，连接AB、CD分别交EF于X、Y，则PX=PY.（注：在相关文献中，多有Klamkin不等式，而文献［1］提到Klamkin蝴蝶定理）.

文献［1］指出：命题2和命题3分别舍弃了P的中点性和交点性，得到了看起来不太兼容的两个结论. 是否存在一个定理可将二者整合起来，文献［1］给出“圆内蝴蝶定理”和“圆外蝴蝶定理”结论.

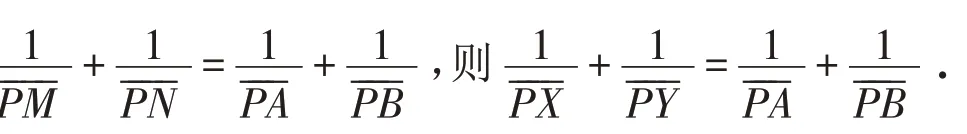
命题5 对⊙O外一条直线l 作垂线OP，过点P作⊙O弦AD、BC，连接AB、CD分别交EF于X、Y，则PX=PY.

2 问题讨论

文献［1］所讨论的问题涉及内容广泛，对研究蝴蝶定理变形命题有一定意义，但文中也出现错误的结论.

2002年，单壿在《平面几何中的小花》［2］给出命题5的证明. 2007年，蒋红瑛在《蝴蝶定理的一个推广及应用》［3］给出命题3的证明.

在命题4中，当点M、N合于弦EF上点P时，此时结论：

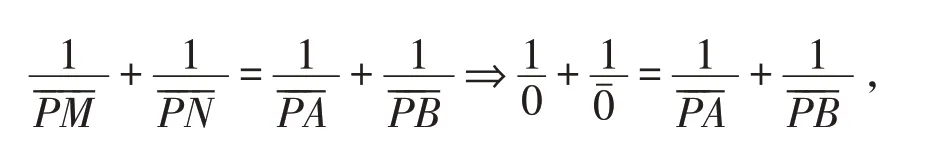
显然，等式不成立. 即命题4并非是蝴蝶定理的统一形式.

3 理论建立

现将圆推广为一般的二次曲线，用射影几何对合对应方法给出统一的结论.

命题6 如图2、图3，过二次曲线弦AB外一点M引二次曲线的两弦CD，EF分别交弦AB于G、H，CF、ED分别交AB于P、Q，设点N为GH的中点，记AN=a，BN=b，GN=NH=d，PN=x，QN=y，其中小写字母均表示有向线段值，则

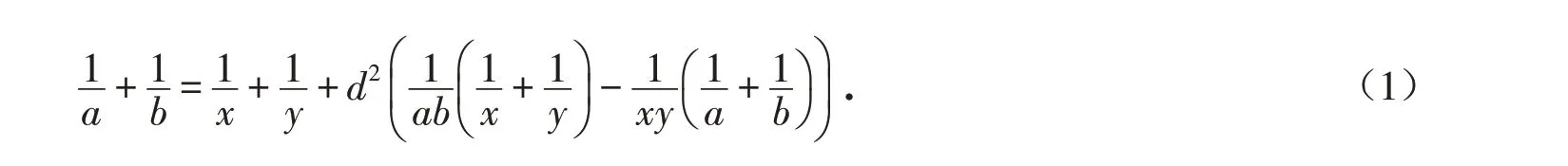
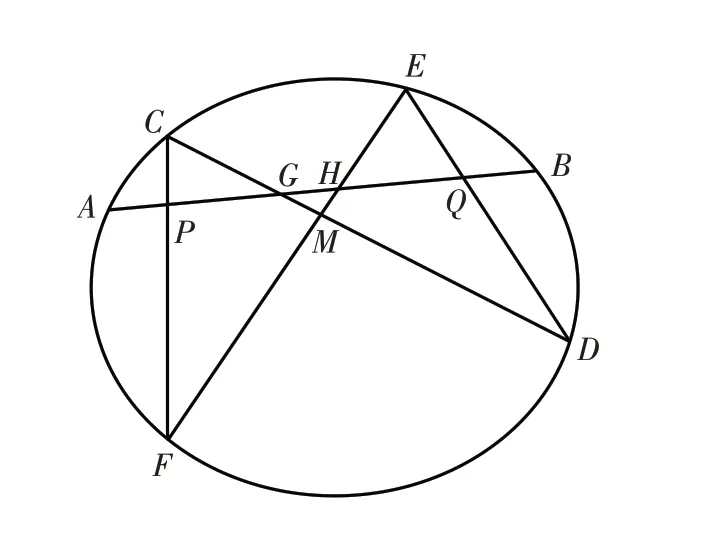
图2 内型蝴蝶定理Fig.2 Inner butterfly theorem

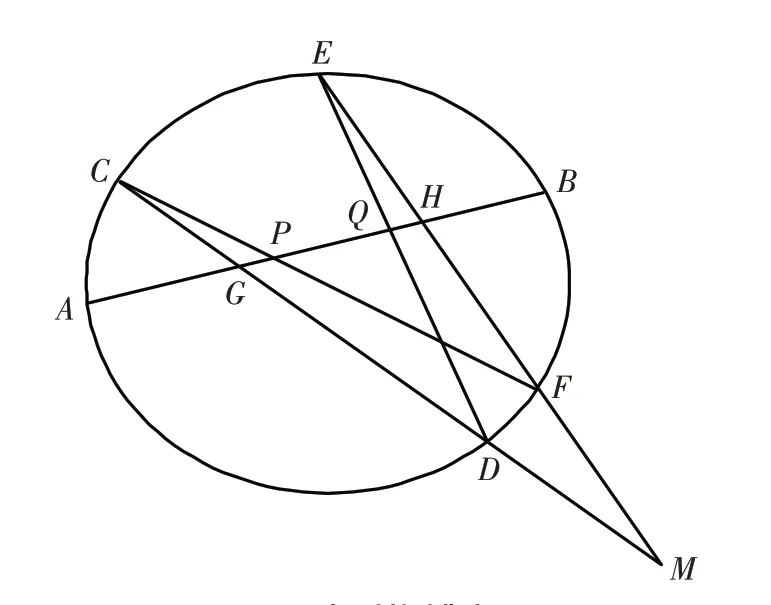
图3 外型蝴蝶定理Fig.3 Exterior butterfly theorem

证明 如图2、图3，将点C、E看成二次曲线上的两个对应线束，则由线束与点列透视对应关系［4］得到：

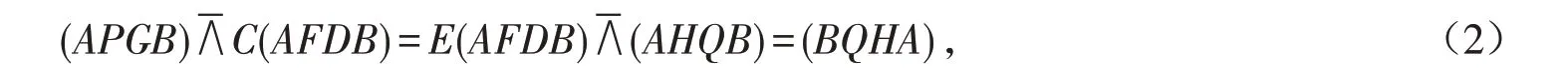
即有对合对应关系：A→B、B→A、P→Q、G→H. 此时，设GH 中点为N，记NA=a，NB=b，GN=NH=d，NP=x，NQ=y，则由对合对应关系［4］：

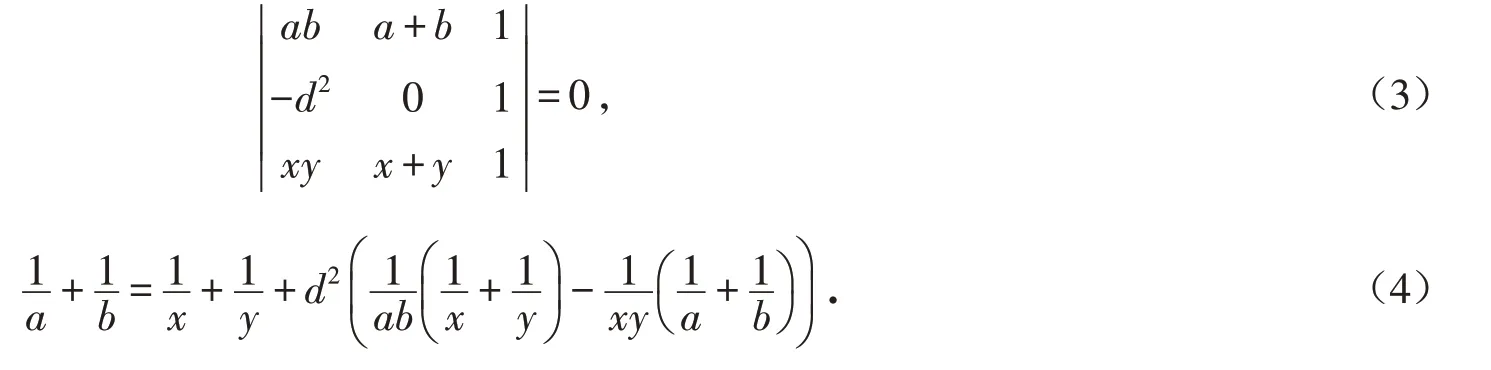
显然，命题6将蝴蝶定理的二次曲线内型形式和外型形式统一起来，其结构与文献［5］基本一致.

值得注意的是：在命题6中，二次曲线弦AB可以是二次曲线外的线段AB. 故有结论.

推论1 过二次曲线外的线段AB外一点M引二次曲线的两弦CD、EF分别交线段AB于G、H，CF、ED分别交线段AB 于P、Q，设点N 为GH 的中点，记AN=a，BN=b，GN=NH=d，PN=x，QN=y，其中线段均表示有向线段，则

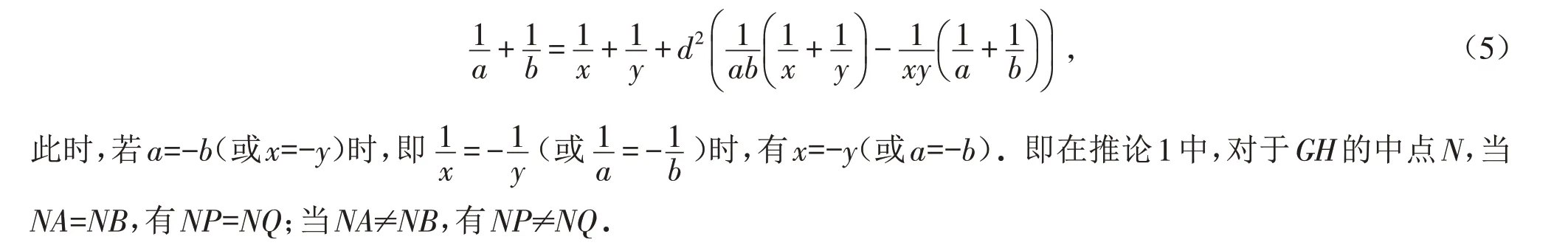
在命题5中，由于点A、B为关于点M对称的共轭虚点，即仍然有MA=MB，因此有结论MP=MQ. 即命题5是推论1的特殊情况，而且这里证法是文献［6］的另外一种射影几何证明方法.

另外，由于（2）式对不同的对应元素，确定一个对合对应关系式，则有结论.

推论2 如图2、图3，过四点C、D、E、F的二次曲线交直线l 于A、B两点，过直线AB外一点M引该二次曲线的两弦CD，EF分别交线段AB于G、H，CF、ED分别交线段AB于P、Q，设点N为GH上一点，记AN=a，BN=b，GN=c，NH=d，PN=x，QN=y，其中线段均表示有向线段，则

推论3 过四点C、D、E、F的二次曲线束Γi(i=1,2,…)交直线l 于Ai、Bi(i=1,2,…)两点，对于直线l 上一点N，记NAi=xi、Bi=yi(i=1,2,…)，其中线段均表示有向线段，则二次曲线束Γi(i=1,2,…)中的任意3条，满足关系：

由于Γi(i=1,2,…)都经过四点C、D、E、F，则每一条Γi(i=1,2,…)关于直线l 的两点Ai、Bi(i=1,2,…)的有向线段坐标都满足（6）式，而由对合对应关系（6）式的唯一性，取二次曲线束Γi(i=1,2,…)中的任意3条，其关于直线l 的两点Ai、Bi(i=1,2,3)的有向线段坐标都满足（6）式，即（7）式成立.

4 理论应用

例1 如图4，PQ 是非退化的二阶曲线Γ1的弦，M、E、F 是PQ上的点，M是PQ的中点，同时也是EF的中点. 过点F的弦交Γ1于A、B，过点E 的弦交Γ1于C、D. 令过B、C、A、D 四点的任一二阶曲线Γ2与直线PQ的交点为S、T，则点M亦为TS的中点［7］.

证明 如图4，将直线对AD、BC 看作退化的二次曲线，则三对二次曲线在直线PQ的有向线段坐标满足：

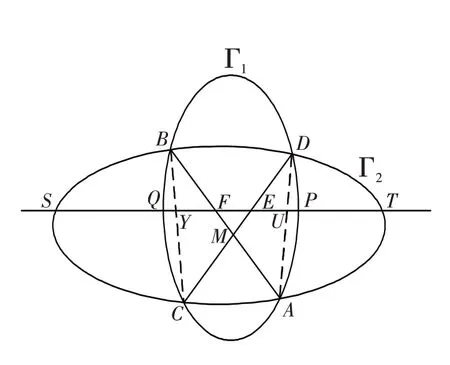
图4 两条蝴蝶定理形式Fig.4 The form of two butterfly theorems

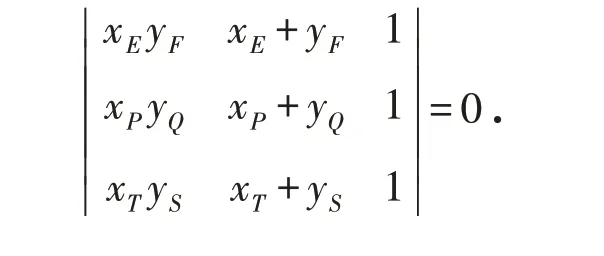
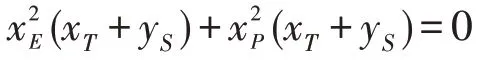
例2 如图5，如果直线l 与二次曲线c1相交于点A1、B1，与二次曲线c2相交于点A2、B2. 那么对由c1、c2所形成的二次曲线束中的任一条二次曲线c3，设它与l 的交点为A3、B3，探讨二次曲线在直线l 上交点的关系.

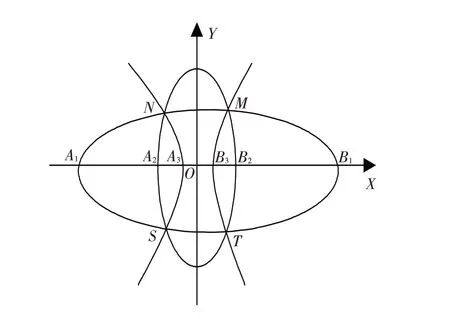
图5 三条蝴蝶定理形式Fig.5 The form of three butterfly theorems

证明 如图5，在直线l 取点O，记有向线段OAi=ai，OBi=bi(i=1,2,3)，则有：

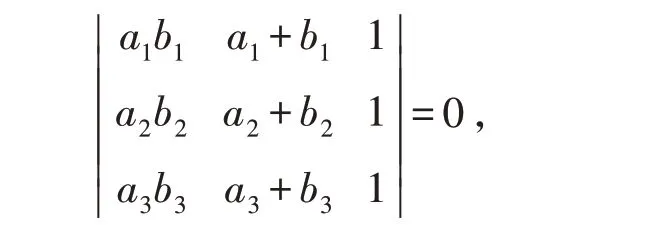
则

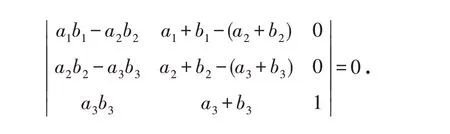
即

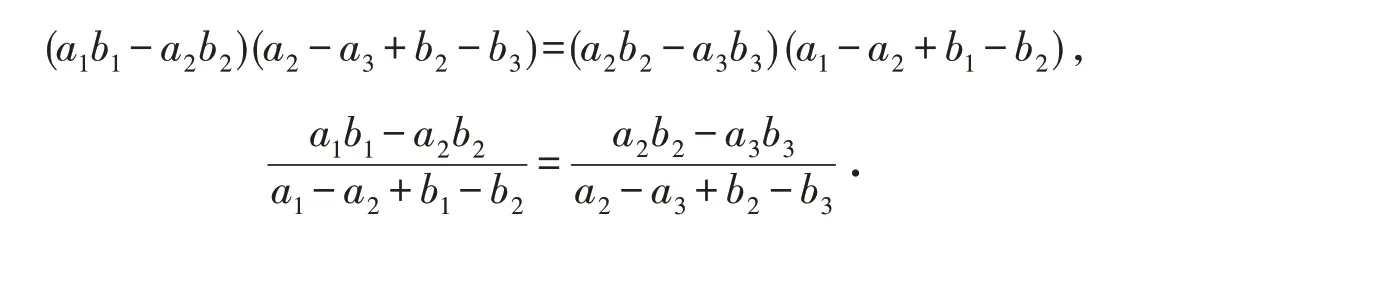
同理，有

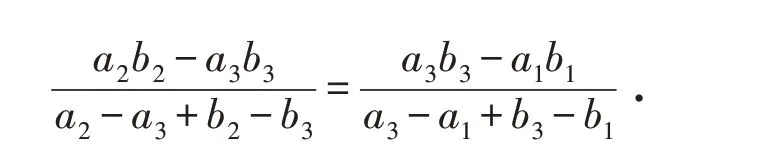
即有结论：

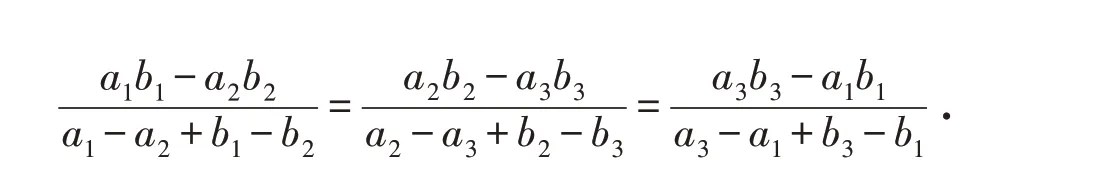
其几何意义：二次曲线中的任意两条与直线l 上交点坐标的有向线段满足不变量关系：

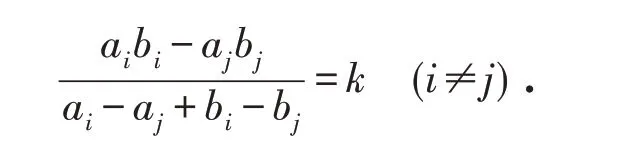
推论4 过四点C、D、E、F的二次曲线束Γi(i=1,2,…)交直线l 于Ai、Bi(i=1,2,…)两点，对于直线l 上一点N，记NAi=xi、Bi=yi(i=1,2,…)，其中线段均表示有向线段，则二次曲线束Γi(i=1,2,…)中的任意2条，满足不变量关系：

文献［8］和［9］利用解析几何讨论了例2的代数形式，没有给出其相应的几何本质特征. 因此，我们曾经在文献［10］和［11］中提出：模型、联想、转化是数学解题创新的关键点.

另外文献［2］所给出的关系式：

是否成立，需要进一步探讨.