改进的基于可分属性的立方攻击*

穆道光，李 枫，张文政

（保密通信重点实验室，四川 成都 610041）

0 引言

立方分析是2009 年欧密会上以色列密码学者Dinur 和Shamir 提出的一种密码算法分析方法[1]，目前已成为对称密码算法中一种常见的分析方法，针对许多典型的流密码算法、哈希算法、认证加密算法等，采用立方分析能得到很好的分析效果。

传统的立方分析是在选定立方变量集后，通过概率测试方法判断其超级多项式（superpoly）是否是关于密钥比特之间的线性或者二次关系式，最后使用代数方法求解关于密钥比特之间的线性或者二次关系式，恢复出密钥比特。攻击者能够选取的立方变量集的大小取决于其实际计算能力，当前一般不超过40。

2017 年美密会上，日本密码学者Todo 等人提出了基于可分属性的立方分析方法[2]。借助于混合整数线性规划（Mixed Integer Linear Programming，MILP）求解工具，该方法可以判断出较大规模立方变量集（如≥70）对应的超级多项式中包含的密钥比特变量。2018 年美密会上，王庆菊等对Todo 等的基于可分属性的立方分析方法作了改进[3]，提出了标记技术（flag technique）、单项式枚举（term enumeration）、代数次数评估（degree evaluation）等方法，能够进一步判断出立方变量集对应的超级多项式的代数式次数、可能包含的单项式及数量。2019 年，叶等人改进了王庆菊等提出的单项式枚举方法[4]，使得在更短的时间内可以得到立方变量集对应的超级多项式可能包含的单项式及数量，但是判断的超级多项式中可能包含的单项式及数量并没有减少，因此攻击所需要的时间复杂的并没有降低。

针对基于可分属性的立方攻击，本文提出了一种改进的单项式枚举算法，该算法相较于之前的算法，能够将更多的不存在于超级多项式中的单项式排除，从而得到的单项式数量更少，新的攻击所需要的时间复杂得到降低。

在第2 节介绍相关的基本知识，在第3 节中给出改进的单项式枚举算法，在第4 节中通过对初始化5 拍MORUS-640-128 算法的分析，验证了改进的单项式枚举算法的有效性，并将改进的单项式枚举算法用于初始化6 拍MORUS-640-128 算法的分析，得到的攻击时间复杂较文献[4]的分析结果有明显地降低。在第5 节中对本文进行了总结。

1 基本知识

1.1 比特可分属性及其传播路径

可分属性的概念由日本学者Todo 等在2015 年的欧密会上提出[5]，它是对积分区分器的一种推广。随后Todo 等针对比特向量集又提出了比特可分属性[6]，2016 年向泽军等建立了比特可分属性传播的混合整数规模（MILP）模型[7]。

定义1： 比特可分属性，令X为上的一个多重向量集；对x，记u[i]，x[i]、u[i]表 示x、u的 第i个 分 量；集 合K={k0,k1,k2,…}，其中，i=0,1,2,…。当πu(x)=xu满足下面的关系式(1)时，称X具有可分属性。

定义2：可分属性传播路径，假设一个迭代密码算法的轮函数为f(X,V)，输入的多重集X具有起始可分属性，经过i轮作用后得到的输出集具备可分属性，r轮可分属性传播如下：

1.2 基于可分属性的立方攻击

基于可分属性的立方攻击方法主要依据以下性质1。

性质1：令f(X,V)为关于n元密钥比特变量和m元公开IV 变量的布尔函数，集合I={i0,i1,…,i|I|-1} ⊆{0,1,…,m-1}为立方变量集合，pI为I对应的超级多项式。xj为第j个密钥比特变量。如果不存在可分属性传播路径，则pI中不包含密钥比特xj。

运用性质1，攻击者可以找出pI中包含的所有密钥比特，我们用集合J表pI示中包含的所有密钥比特。

将性质1 作一般性推广，有如下性质2。

性质2：令f(X,V)为关于n元密钥比特变量和m元公开IV变量的布尔函数，集合I={i0,i1,…,i|I|-1} ⊆{0,1,…,m-1}为立方变量集合，pI为I对应的超级多项式。集合T={j0,j1,…,j|T|-1} ⊆{0,1,2,…,n-1}，如果不存在可分属性传播路径，则pI中不包含单项式xj0,xj1,xj2,…,xj|T|-1。

根据性质2，王庆菊等在文献[3]中提出了pI的代数式次数上界判断方法，通过在比特可分属性传播的MILP 模型中设置目标函数为，求解MILP 模型，目标函数返回值即为pI的代数式次数上界d,d≥deg(pI)。

根据性质2，王庆菊在文献[3]中提出了一种单项式枚举方法，通过在比特可分属性传播的MILP 模型中增加约束，其中0 ≤t≤d，该MILP 模型的一个可行解即对应了pI中可能存在的一个次数为t的单项式，该MILP 模型的所有可行解对应了pI中所有可能存在的次数为t的单项式，记pI中次数为t的单项式集合为Jt。

对选定的一个立方变量集I，在立方攻击离线阶段需要的时间复杂度为；在立方攻击离线阶段需要的时间复杂度为，假设I对应的超级多项式pI为平衡布尔函数，该立方变量集I恢复1 比特密钥信息的时间复杂度为。

1.3 标记技术

考虑比特运算：(s1,s2)→(s1,s2,s1·s2)，根据比特可分属性传播规则，当输入的比特可分属性为(0,1)时，输出的比特可分属性为{(0,1,0),(0,0,1)}；当输入的比特可分属性为(1,0)时，输出的比特可分属性为{(1,0,0),(0,0,1)}。

当s1取固定值0 时，s1·s2恒为0。因此，s1取固定值0，输入比特可分属性(0,1)时，输出的比特可分属性为(0,1,0)，即这时候不存在可分属性传播路径(0,1)→(0,0,1)。

类似地，当s2取固定值0 时，s1·s2恒为0。因此，s2取固定值0，输入比特可分属性(1,0)时，输出的比特可分属性为(1,0,0)，即这时候不存在可分属性传播路径(1,0)→(0,0,1)。

针对这种情况，王庆菊等在文献[3]中提出了标记技术，在每个比特位置υi，额外增加一个辅助标记符号υi.F。当该位置的比特取值恒为0 时，其标记符号υi.F设置为0c，当该位置的比特取值恒为1 时，其标记符号υi.F设置为1c，当该位置的比特取值不固定时，其标记符号υi.F设置为δ。

标记符号在比特运算中传递规则如下：

（1）比特复制运算x→(x,x)：0c→(0c,0c)，1c→(1c,1c)，δ→(δ,δ)；

（2）比特异或运算x·y→z：(1c,1c)→0c，(0c,α)→α，(α,0c)→α，(δ,α)→δ，(α,δ)→δ，这里α∈{0c,1c,δ}。

（3）比特与运算x·y→z：(δ,δ) →δ，(1c,α)→α，(α,1c)→α，(0c,α)→0c，(α,0c)→0c，这里α∈{0c,1c,δ}。

通过设置标记符号，当遇到(s1,s2)→(s1,s2,s1·s2)运算时，如果s1或者s2的标记符号为0c，将排除比特可分属性传播路径(0,1)→(0,0,1)或者(1,0)→(0,0,1)。

2 改进的单项式枚举算法

性质2 给出了判断立方变量集I对应的超级多项式pI中不包含单项式xj0,xj1,xj2,…,xj|T|-1的理论依据。但反过来，对于一个集合T={j0,j1,…,j|T|-1}⊆{0,1,2,…,n-1}，如果存在可分属性传播路径，pI中不一定包含单项式xj0,xj1,xj2,…,xj|T|-1。例如假设超级多项式pI=x1x2x3+x1x4，对T∈{{1,2},{1,3},{2,3},{1,4}}，都存在可分属性传播路径(WTn||WIm)→1，但pI中不包含单项式x1x2、x1x3、x2x3。

集 合T={j0,j1,…,j|T|-1} ⊆{0,1,2,…,|J|-1}。记J为pI中包含的密钥比特集合，假设J={x0,x1,…,x|J|-1}，则超级多项式pI可以分解为pI=xj0,xj1,…,xj|T|-1g(X´)+h(x0,x1,…,x|J|-1)，其中g(X´)为变量取自X´=J-T上的布尔函数，h(x0,x1,…,x|J|-1)中的项均不包含因子xj0,xj1,…,xj|T|-1。

只有当固定所有的x∈X´为0 时，g(0)=1，即pI中仍然包含单项式xj0,xj1,…,xj|T|-1，则说明xj0,xj1,…,xj|T|-1∈Jt。因此，我们有下面的命题1。

命题1 令f(X,V) 为关于n元密钥比特变量X∈和m元公开IV变量V∈的布尔函数，集合I={i0,i1,…,i|I|-1} ⊆{0,1,…,m-1}为立方变量集合，pI为I对应的超级多项式。J为pI中包含的密钥比特集合，不妨假设J={x0,x1,…,x|J|-1}，集合T={j0,j1,…,j|T|-1} ⊆{0,1,2,…,|J|-1}，对所有的x∈X´=J-T,x=0。如果不存在可分属性传播路径，则pI中不包含单项式xj0,xj1,xj2,…,xj|T|-1。

由于所有的x∈X´=J-T,x=0，故pI=g(0)xj0,xj1,…,xj|T|-1+h(x0,x1,…,x|J|-1)。pI中仅有一项xj0,xj1,…,xj|T|-1g(0)满足时，故g(0)=0，表明pI中不包含单项式xj0,xj1,xj2,…,xj|T|-1，即xj0,xj1,xj2,…,xj|T|-1∉J|T|。证明完毕。

由命题1，我们在文献[3]中算法5 的基础上提出了一种改进的单项式枚举算法。

算法：改进的单项式枚举算法

输入：立方变量集I，非立方变量集赋值IV，次数t，pI中包含的密钥比特集J，输出比特位置output。

步骤1：新建MILP 模型 M，一个空集合Jt；

步骤2： 声明m个MILP 变量vi，其中i=0,1,2,…,m-1，代表公开变量；声明n个MILP 变量xi，其中i=0,1,2,…,n-1，代表密钥变量；

步骤3：对所有的vi，i∈I，在 M中增加约束条件vi=1，并将vi的标记符号赋值为vi.F=δ；

步骤4：对所有的vi，i∉I，在 M中增加约束条件vi=0，并将vi的标记符号赋值为vi.F=IV[i]；

步骤6：根据算法轮函数、输出比特位置output，按照可分属性传播规则，更新 M；

步骤7：求解 M模型，如果模型无可行解，跳至步骤13；

步骤8：记可行解中集合{xi|xi=1}为T，新建MILP 模型*M，并对*M 模型运行步骤2 至步骤4，对xi∈J-T，xi.F=0c；

步骤9：对xi∈T，在*M 中增加约束条件xi=1；对xi∉T，在*M 中增加约束条件xi=0；

步骤10：根据算法轮函数、输出比特位置output，按照可分属性传播规则，更新*M ；

步骤11：求解*M，如果模型有可行解，将单项式纳入Jt；

步骤13：输出Jt。

改进的单项式枚举算法相较于之前的算法，能够将更多的不存在于pI中的t次单项式排除，从而改进的单项式枚举算法得到的|Jt|更小。由于立方变量集I恢复1 比特密钥信息的时间复杂度为，因此，采用改进的单项式枚举算法将使得立方变量集I恢复1 比特密钥信息的时间复杂度得到降低。

3 对MORUS-640-128 算法的分析

3.1 MORUS-640-128 算法简介

MORUS 算法是CAESAR 竞赛末轮7 个候选认证加密算法之一，由新加坡南洋理工大学伍宏军等提交。MORUS-640-128 算法是MORUS 算法其中一个版本，使用128 比特密钥和128 比特初始向量IV，内部状态寄存器大小为640 比特。MORUS-640-128算法加密与认证过程包括初始化阶段、关联数据处理阶段、加密阶段、标签生成阶段四个阶段。我们的分析只涉及到MORUS-640-128 算法的初始化阶段，因此只对该阶段进行介绍。

记MORUS-640-128 算法的128 比特密钥为K，128 比特初始向量为IV，640 比特的内部状态寄存器初始状态为，其 中均为128 比特。

MORUS-640-128 算法的初始化阶段分为初始状态载入和16拍状态更新。初始状态载入过程如下：

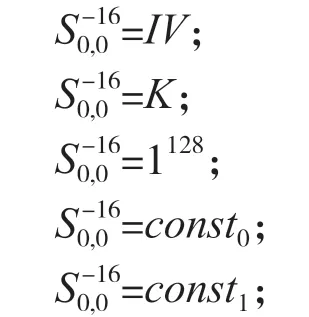
这里1128表示128 比特全1 向量，const0、const1均为128 比特常数。

初始状态载入完毕后进行16 拍状态更新，每拍包含5 轮运算，具体如下（i=-16 至-1）：

其中，b0=5，b1=31，b2=7，b3=22，b4=13；w0=32，w1=64，w2=96，w3=64，w4=32；函数Rotl(X,b)表示将X分为4 个32 比特数，每个32 比特数循环左移b位。

3.2 初始化5 拍MORUS-640-128 算法的分析

对初始化5 拍的MORUS-640-128 算法，我们选取一个3 维立方变量集I={5,8,97}，非立方变量均固定为0，输出比特位置为，i从0 到127 变化，分别通过三种不同的方法计算I对应的超级多项式pI中1 次单项式集合J1。

方法一：直接计算，记输出比特关于密钥K和初始向量IV的布尔函数为f(K,IV)，用CI表示非立方变量均固定为0，立方变量集I中的元素遍历所有可能值所组成的向量集合。

首先，取K为全0，即K=0128，计算⊕IV∈CI f(K,IV)，得到pI中常数项值c=⊕IV∈CI f(0128,IV)；

其次，对j=0,1,2,…,127，依次取K为kj，其中kj表示128 比特向量在第j比特位置取1，其他位置取0，计算⊕IV∈CI f(kj,IV)，得到pI中1 次单项式xj的系数aj=c⊕(⊕IV∈CI f(kj,IV))；所有满足系数aj=1 的xj构成了pI中1 次单项式集合，记得到的集合为。

方法二：采用第3 节中改进的单项式枚举算法，输入立方变量集I，次数为1，pI中包含的密钥比特集J={xj|j=0,1,2,…,127}，非立方变量固定为全0，输出比特位置；得到的集合记为。

方法三：采用文献[3]中的算法5，通过在比特可分属性传播的MILP 模型中增加约束，该MILP 模型的一个可行解即对应了pI中可能存在的一个次数为1 的单项式，该MILP 模型的所有可行解对应了pI中所有可能存在的次数为1的单项式，记得到的集合为。

3.3 初始化6 拍MORUS-640-128 算法的分析

文献[4]中叶等人采用基于可分属性的立方攻击对初始化为6 轮MORUS-640-128 算法进行了分析，选取了24 个立方变量集I和输出比特位置，非立方变量固定取0，给出了它们超级多项式中可能包含的单项式和数量，其结果见文献[4]中附表9。

我们采用3 节中改进的单项式枚举算法，对这些立方变量集I和它们相应输出比特位置，重新判断他们对应的超级多项式中可能包含的单项式及数量。整个分析过程如下：

步骤1：选取文献[4]中附表9 中的一个立方变量集I，非立方变量固定为0，运行文献[3]中算法1，得到I对应超级多项式中包含的密钥比特集J。

步骤2：立方变量集I，非立方变量固定为0，运行文献[3]中算法2，得到I对应超级多项式pI的代数次数上界d。

步骤3：对t=0 至d，运行第3 节中改进的单项式枚举算法，得到pI中可能包含的所有t 次单项式集合Jt。

我们的分析结果见表2。

表1 、、中元素个数

表1 、、中元素个数

表2 初始化6 拍MORUS-640-128 的分析结果

其中，单项式数量num，时间复杂度。最后一列为文献[4]中的攻击时间复杂度。

以立方变量集I={3,4,7,15,20,24,30,31,40,43,50,60,70,79,86,89,95,96,97,102,103,106,111,116}，输出比特位置取为例，该立方变量集I对应的超级多项式pI的代数次数上界为14，下表3 给出了pI中t次单项式数量|Jt|的情况（t=0 至14）。

由表3 可知，我们得到pI中单项式数量为=800，假设I对应的超级多项式pI为平衡布尔函数下，则该立方变量集I恢复1比特密钥信息所需要的时间复杂度为。相比较而言，文献[4]得到的pI中单项式数量为60928，所需要的时间复杂度约为239.9。

表3 t 次单项式数量

4 结语

立方攻击是一种典型的对称密码算法分析方法。针对基于可分属性的立方攻击，提出了一种改进的单项式枚举算法，该算法相较于之前的算法，能够将更多的不存在于超级多项式中的单项式排除，从而导致新的攻击所需要的时间复杂得到降低。针对初始化5 拍MORUS-640-128 算法的分析验证了新的攻击方法的有效性。针对初始化6 拍MORUS-640-128 算法的攻击所需要的时间复杂度较之前的分析结果更低。