单自由度圆柱涡激振动特性及其影响因素分析❋

袁方正， 袁德奎， 曾 攀， 刘长根

(天津大学机械工程学院力学系，天津 300354)

在来流作用下深水立管发生涡激振动 (Vortex induced vibration, VIV) 是一个在海洋工程中普遍的现象，同时也是引起立管产生疲劳损坏的主要原因之一。水流流经钝尾体如圆柱类结构时，会在尾流区发生流动分离并产生周期性泄放的漩涡，尾涡的周期性泄放会导致圆柱受到周期性的荷载，从而诱发涡激振动。涡激振动的多自由度、强非线性的特点决定了它是一个复杂的流固耦合问题。当立管结构发生涡激振动且振动频率接近系统自身的固有频率时，会发生共振，促使结构物产生大幅度的振动，从而对海洋结构物产生破坏。随着人们对海洋资源的开发，对圆柱涡激振动现象的研究也显得更为迫切。

实验是研究涡激振动问题的主要的方法之一，大多数对涡激振动特性和其产生机理的认识都是来源于实验。Feng[1]在风洞中展开了高质量比低阻尼比的单自由度涡激振动实验，该实验发现振动存在两个响应分支，并观测到分支在切换时存在迟滞(Hysteretic loop)现象。Williamson团队在水中对圆柱的涡激振动进行了大量实验研究[2-5]，发现圆柱进行涡激振动的锁定区间范围与质量比m*有关。现有的实验不仅增加了学者对圆柱涡激振动特征和机理的认知，也为检验和发展相应的数值模拟方法奠定了基础。计算机性能的提高使CFD(计算流体力学)方法成为研究涡激振动的主要方法之一。Sanchis等[6]认为质量比是影响圆柱体振动特性的重要因素。陈正寿等[7]讨论了质量比不同的圆柱在相同约化速度下，由于单双自由度的不同所造成的振动特性的差别，简要分析了顺流向振动对横流向振动的影响程度。曹淑刚等[8]探讨了不同质量比对圆柱涡激振动的顺流向频率的影响。此前的研究工作对有关质量阻尼比m*ζ与阻尼比ζ对振动特性影响的研究较少，也没有从理论，实验，数值模拟3个方面综合考虑这一问题。

本文在已有研究的基础上，对流体荷载进行线性分解推导得到了锁定区间柱体响应的频率比、振幅与流体荷载和系统物性参数之间的定性关系。根据推导得出的结果，结合相关的经典实验，对圆柱涡激振动特性的影响因素(质量比，阻尼比，质量阻尼比)开展了系统的数值实验，对比了不同因素下圆柱锁定区间、振幅、升阻力系数等关键参数和特征，进一步分析了不同质量比，阻尼比，质量阻尼比对圆柱涡激振动特性的影响。

1 线性化分析

基于单自由度刚性圆柱振动的轴向对称性，可将模型简化为图1所示的二维单自由度振动系统。

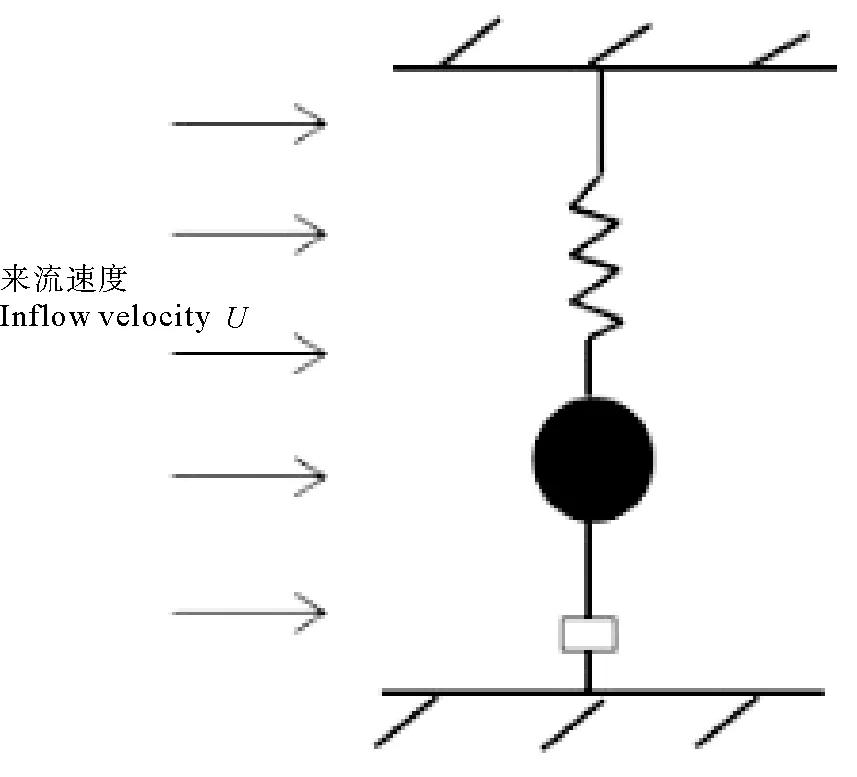
图1 单自由度横向振动的物理模型

弹性支承的二维圆柱单自由度振动系统实际上是一种弹簧-质量-阻尼系统，其振动方程为：

(1)

式中：m为单位长度的圆柱质量，y为圆柱偏离平衡位置的位移，k为弹簧刚度系数，c为振动系统的阻尼系数，Fy(t)为圆柱受到的升力。

在锁定区，将圆柱的振动近似认为简谐振动，且泄涡频率完全被固定在圆柱振动频率上。因此假设圆柱横向位移y的表达式为：

y=Asin(ωext)。

(2)

式中：A为圆柱的振幅；ωex为圆柱的振动圆频率。圆柱所受升力无量纲化后的升力系数为：

CL=Clsin(ωext+φ)。

(3)

式中：Cl为升力系数的幅值；φ表示升力系数与位移时间历程的相位角。根据Parkinson[9]的方法：将升力系数进行分解，如下：

CL=Clvcos(ωext)+Cla[-sin(ωext)]。

(4)

由式(4)和式(5)可得：

Clv=Clsin(φ),Cla=-Clcos(φ)，

(5)

φ=arctan(-Clv/Cla)。

(6)

式中：Clv为横向流体荷载的阻尼分量，体现系统能量的积累与耗散；Cla为横向流体荷载的惯性分量，与附加质量有关。

下面对该式(1)进行无量纲化：

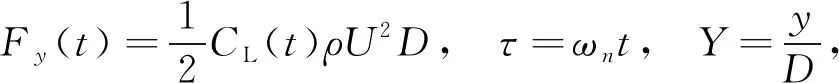
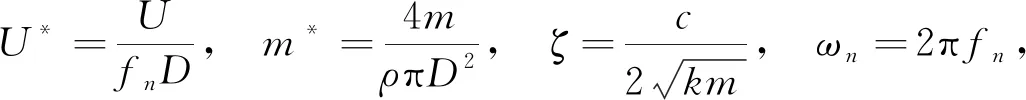
式中：CL为无量纲升力系数；Y为无量纲位移，U为来流速度；D为圆柱直径；U*为约化速度；fex为圆柱实际振动频率；fn为圆柱固有频率；ωn为固有圆频率；ρ为流体密度。将振动方程进行无量纲化，可得：

(7)

再将式(2)与式(4)无量纲结果代入式(2)中，可得：

(8)

(9)

式(8)和式(9)反映了频率比、振幅与流体荷载和系统物性参数之间的关系，可以定性反映出锁定区间柱体的振动特性。但是引入了相关假设，因此流体荷载系数分解得到的上述两式只能在当流体荷载频率完全被圆柱振动频率所捕获时才有定性参考作用。由于分析需要，暂且假定当圆柱处于锁定区间内时，流体荷载频率(泄涡频率)与振动频率及圆柱固有频率都相等(这在高质量比是近似成立的，但在低质量比情况下会有差异)，并且圆柱的振动可以由正弦函数来表示。则由式(8) 可知，在锁定区间组合因子m*ζ越大，可能导致A*越小；由式 (9) 可见，在锁定区间假定频率比固定，则m*越大可能使得U*越大，进入锁定的约化速度越大即锁定段延后，锁定区间变窄。

2 实验结果分析

美国康奈尔大学的Williamson教授等沿用了Feng的经典实验设计，对低质量比低阻尼比圆柱的涡激振动进行了大量实验研究。根据上一节的线性化分析得出的结论将Williamson系列实验的结果进行了分类整理(见图2)。

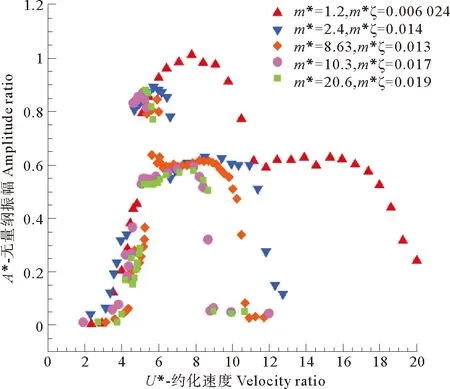
图2 Williamson实验结果

从图中可以看出：圆柱振动系统的组合因子m*ζ和质量比m*的不同会导致圆柱振动特性出现较大差异。具体表现为组合因子m*ζ决定了圆柱的振幅，在质量比一定的情况下，其越小则振动的幅值越大；而在组合因子一定的情况下，圆柱的锁定区间范围主要受质量比m*的影响，质量比越小则锁定区间的范围越大。这表明线性化分析的结果与实验结果相符，都反映出涡激振动特性受到m*ζ和m*的影响较大。下文将对不同的质量比和质量阻尼比的圆柱进行系统的数值模拟，以期从数值模拟的角度上对影响涡激振动特性的因素进行定量的分析。

3 数学模型及求解方法

3.1 流动控制方程

将问题简化为不可压缩流体在与圆柱轴线垂直的平面内的二维流动，可写出如下的雷诺平均纳维斯托克斯方程(RANS)：

(10)

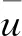
3.2 湍流模型

根据文献[10]所得出的结论，采用SSTk-ω湍流模型对RANS方程进行封闭。SST(Shear Stress Transport)k-ω模型通过添加一个混合函数使得模型在近壁面处为k-ω模型，而在远离壁面的充分湍动区则为高雷诺数k-ε模型，是对k-ω模型的改进，输运方程如下：

(11)

式中：k为湍动能；ω为比耗散率；和分别为k、ω方程的湍流普朗特数；μt为湍流黏性系数；F1为混合函数。模型对湍流黏度的定义考虑了湍流剪切力的输运，湍流模型的细节详见文献[11]。该模型考虑了湍流剪切力效应，在模拟逆压梯度、边界层分离、近壁区的绕流旋流等有较大优势。

3.3 模型设置及求解方法

计算网格划分见图3。整个计算域长40D、宽20D，圆柱圆心距离计算域上边界和右边界离分别为10D和30D。采用混合网格画法，在圆柱外设置半径为4D的圆形区域，此区域划分为结构化网格，使其随着圆柱一起运动，从而保证了边界层网格的稳定，且适当减小由于网格运动产生的网格畸变率导致的数值不稳定，并且对圆柱周边网格进行加密以保证计算的空间分辨率。外部区域为三角形非结构网格，以保证使用动网格弹性光顺技术时的灵活性。

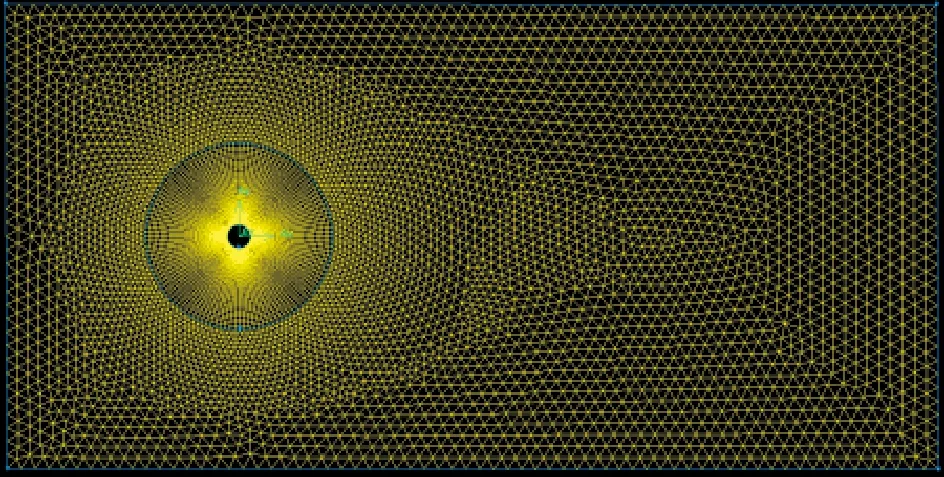
图3 计算域网格

利用有限体积法求解涡激振动的流场：时间离散采用二阶隐式格式，用二阶迎风格式对对流项进行离散，同时用SIMPLEC算法求解压力速度耦合方程。用四阶Runge-Kutta法求解结构振动方程。每一个时间步内的具体求解过程为：(1)求解RANS方程获得流场；(2)对柱面的应力积分以获得升力；(3)将无量纲化的升力代入结构振动方程中，求解振动方程获得圆柱的位移和速度；(4)将圆柱的运动信息传递给求解器，再用动网格功能实现网格更新。如此反复迭代，直至达到设定的收敛精度，实现流固耦合计算。其中后三步都是基于C语言环境编写代码实现。

3.4 网格收敛检验

数值计算精度和效率很大程度上依赖于网格的质量。为兼顾分辨率和计算效率，在开展正式的模拟之前对网格收敛性进行检验是必需的。本文针对所要开展的模拟工作按以下步骤系统检验了网格收敛性。

首先分析了边界网格(主要是第一层的网格无量纲高度y+和圆周网格数)对计算精度和效率的的影响，并从中选择最接近实验结果的壁面边界处理方法。参数设置参考Williamson[2]的实验：圆柱直径D=0.038 1 m，阻尼比ζ=0.005 4，质量比m*=2.4，约化速度为9，雷诺数处于亚临界范围。

根据经验，y+是1的量级，y+要在模拟结束后才可获得，因此具体使用时可先采用经验公式[12]：

y+=0.172Re0.9(y1/D)。

(12)

对网格第一层高度进行估算，得到结果后再不断调整网格直到达到符合条件的y+值。本文设置了两组工况分别研究了y+、圆周网格数不同引起结果的差异，计算结果见表1。

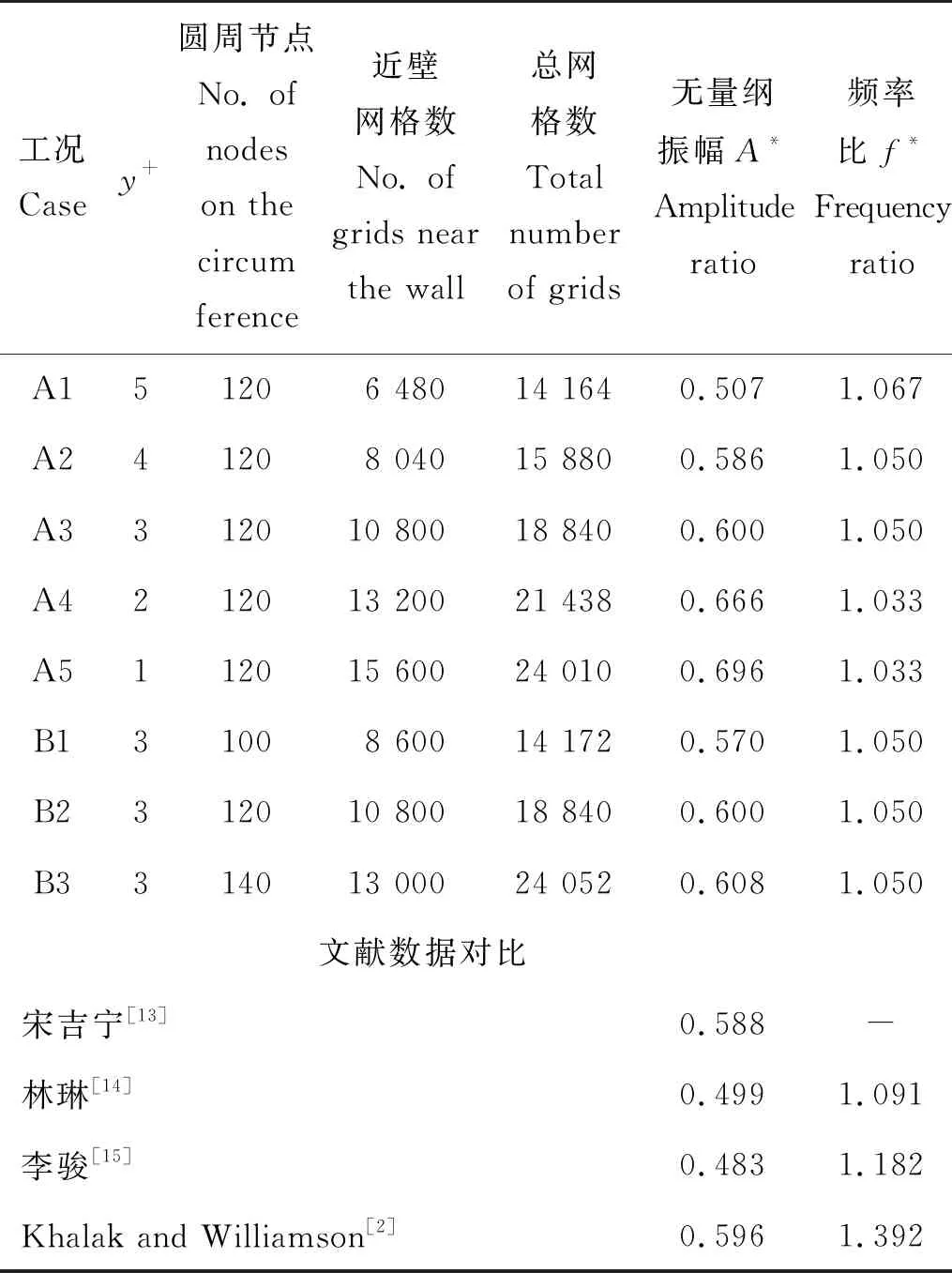
表1 不同工况下的结果及对比

A组工况对比了y+的不同，可知y+为3时结果较理想；B组工况比较了不同的圆周网格数的影响，主要考察计算效率，可知当圆周网格数为120时，网格满足收敛要求。综合来看，采用B2工况进行后续计算可以满足网格收敛性要求。

4 计算结果及分析

4.1 不同质量比、组合因子对涡激振动特性的影响

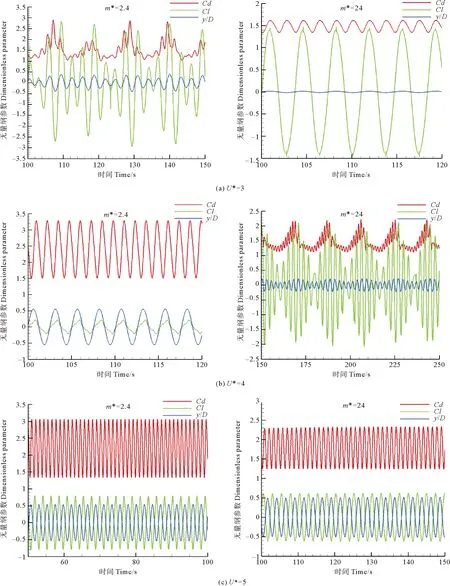
为了对涡激振动的影响因素进行分析，首先研究了固定阻尼比ζ=0.000 54的情况下，不同质量比圆柱涡激振动特性的差异。对比了高低两种质量比工况：m*=2.4，ζ=0.000 54 (m*ζ=0.001 3) 和m*=24，ζ=0.000 54 (m*ζ=0.013)。得出了不同质量比圆柱的振幅随约化速度的变化曲线，结果见图4。

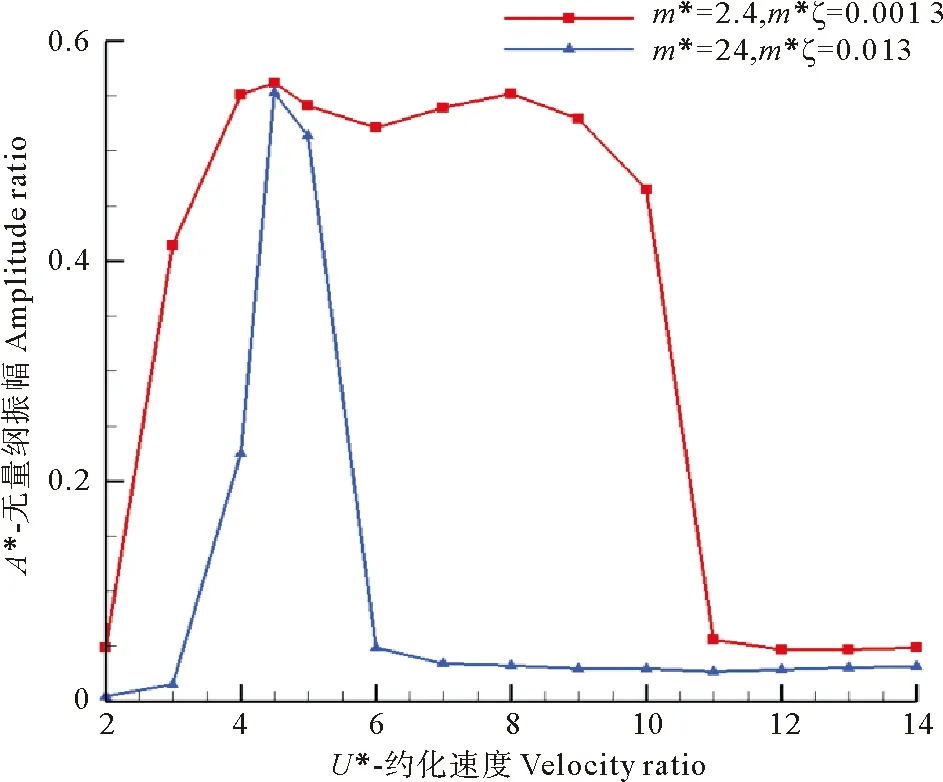
图4 ζ=0.000 54时不同质量比圆柱的振幅响应

从图4可以看出当固定ζ=0.000 54改变质量比时，圆柱振动特性发生了较大变化。当质量比减小时，圆柱在锁定区的最大振幅略微上升，整体振幅也有较大增长；从锁定段来看，随着质量比减小，圆柱的锁定区间有了大范围的扩展，大质量比情况对应锁定段约为U*∈[4.5,5]，而小质量比情况约为U*∈[4,10]，锁定区间长度相差了一个数量级。

图5给出了不同约化速度下2种质量比圆柱振动的力系数和位移的时间历程曲线。可以看出，对于不同的质量比，都存在差拍和位移升力相位角180°转变等现象。对于m*=24的圆柱，当U*=3时位于初始分支，振幅很小；当U*=4，可以观察到力系数和位移都出现了明显的多频振动的拍现象，表明振动进入过渡区，振幅有所增大；而后振幅再次增大，差拍现象消失，曲线重新变为稳定简谐振动状态，表明圆柱进入锁定区；最后当U*=6时，位移大幅减小，圆柱进入解锁区。对于m*=2.4的圆柱，当U*=3时进入过渡区；当U*=12时，圆柱已经进入解锁区。

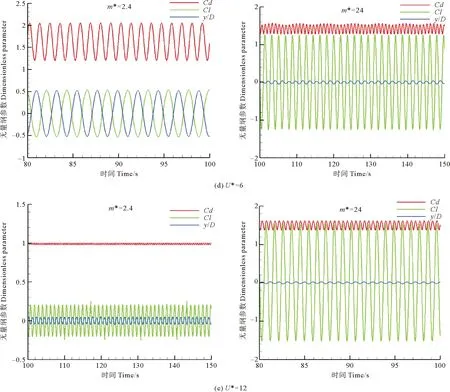
图5 不同约化速度下Cd、Cl、y/D的时间曲线

以上分析表明：在固定ζ=0.000 54的情况下改变质量比m*，质量比m*和组合因子m*ζ均发生了变化，由此导致锁定区的振幅和锁定范围都发生变化。

为了进一步验证理论分析与实验给出的结论，接下来将分别对m*和m*ζ的影响进行讨论。

4.2 质量比对涡激振动特性的影响

在固定组合因子m*ζ=0.013的情况下，选取了m*=1.2、2、2.4、6、24五种质量比，通过数值模拟来研究不同质量比对涡激振动特性产生的影响。

图6给出了质量比的变化所导致的涡激振动特性的差异。从图中可见，随着质量比逐渐减小，圆柱的锁定范围有逐渐扩大的趋势，但在锁定区的最大振幅基本相同。此外，可以观察到锁定区间的扩大是“两头延伸”的，即低质量比比高质量比更早进入锁定且退出锁定的约化速度延迟。从锁定范围扩大的位置来看，扩大的锁定区主要发生在高流速一端。当质量比减小到1.2时，锁定区间覆盖了整个约化速度范围，并可以观察到其振幅变化趋势是逐渐减小而非快速减小到非锁定段。在图6同时也表明了振动圆柱的最大振幅由组合因子m*ζ决定，当组合因子相等时，圆柱处于锁定状态的最大振动幅值基本相等，锁定区间内的振幅也基本相等。

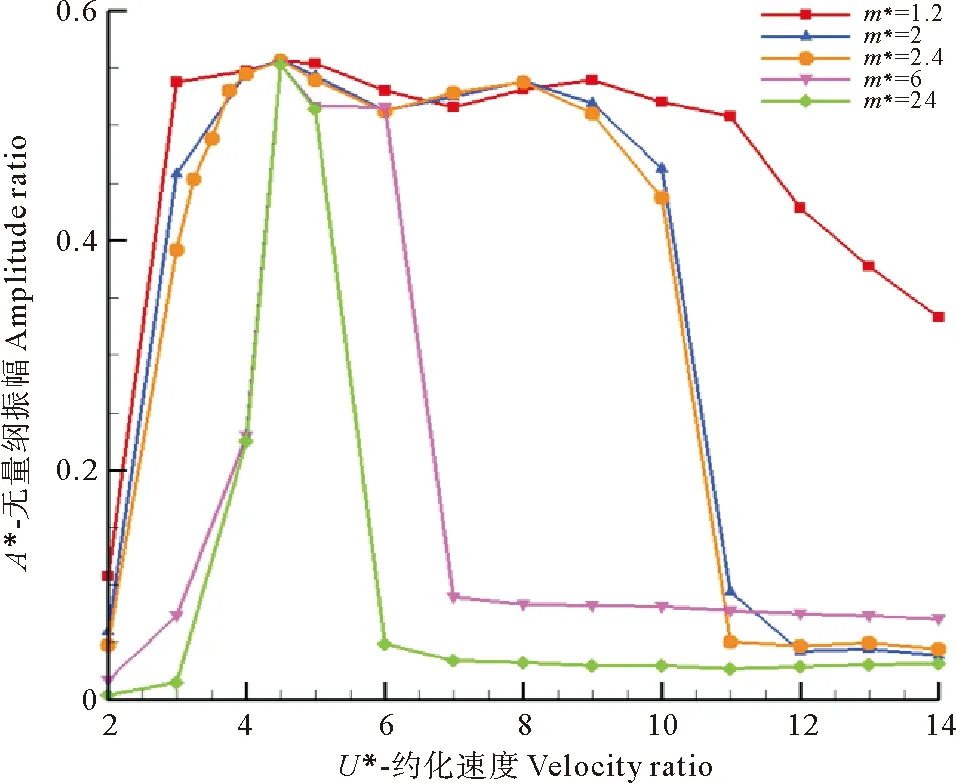
图6 时不同质量比圆柱的振幅响应

在线性化分析时，由式 (9) 得出的m*越小，锁定区间变大这一结论只在高质量比的条件下(假定此时泄涡频率完全固定在圆柱固有频率上)成立，而从图中可以看出，质量比较低时，锁定区间的范围仍会随着质量比的减小逐渐变大，这表明线性化分析得出的锁定区间范围的大小与质量比成负相关关系的结论可推广至低质量比的情况。

4.3 组合因子对涡激振动特性的影响

最后，为了研究组合因子的影响，对固定质量比m*=2.4并采用不同的阻尼比即不同组合因子的情况进行了涡激振动的数值模拟。

图7给出了当m*=2.4时，圆柱在3种不同组合因子下的涡激振动响应。从中可以看出，在固定m*=2.4的情况下，3种组合因子得到的响应幅值随约化速度的变化趋势是一致的。而且可以看出高低振幅切换的位置也相同，对应锁定区间的范围一致。从振幅的角度来看，在锁定区间内，随着组合因子的减小，整个区间的振幅呈现增大趋势，但是增大的幅度十分有限。脱离锁定后，3种组合因子得到的解锁区振幅响应差异不大。

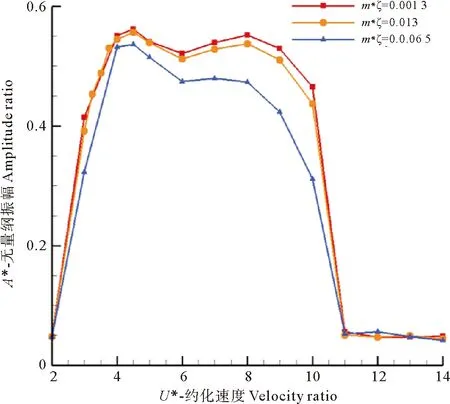
图7 m*=2.4时不同组合因子圆柱的振幅响应

5 结论

本文在前人实验结果的基础上，采用线性化分析和数值模拟相结合的方法，对影响涡激振动特性的参数进行了分析，结果表明：

(1)锁定区间柱体响应的频率比、振幅与流体荷载和系统物性参数之间具有确定的关系：圆柱的振幅与质量阻尼比成负相关关系，锁定区间范围的大小与质量比成负相关关系。

(2)当圆柱处在锁定状态时，其振幅大小由组合因子m*ζ决定。组合因子越小，圆柱的振幅越大，反之则越小，但是组合因子对振幅的影响幅度有限；柱体锁定区间范围的大小由质量比m*决定，质量比越小，锁定范围越大，反之则越小，质量比对锁定区间范围的大小有显著影响，影响的主要范围是在约化速度较大一端。

(3)数值模拟的结果与线性化分析和实验结果一致，并且表明线性化分析得出的锁定区间范围的大小与质量比仍成负相关关系的结果可推广至低质量比情况下。此外，数值模拟不仅捕获了涡激振动中的“拍”现象，并且可反应出上下端分支位移与升力之间相位发生180°变化。