例谈几何画板在圆的轨迹问题中的应用
兰州市第五十一中学
圆的轨迹问题是高中数学中学生较难理解的一种问题类型.在以往的教学中,教师习惯于告诉学生“死”的结论,让学生在记忆的基础之上进行运用.学生由于缺乏“动”的直观感受,对此类问题往往一知半解,缺乏深入认同和深刻理解.本文以圆的方程一章中的轨迹问题为例,采用几何画板演示的方法,加深学生的直观印象,并通过变式训练,让学生彻底掌握圆的轨迹问题的求解方法,并能灵活运用.
1.直接法
例1平面中已知线段AB,且| |AB=4,若动点P满足,求动点P的轨迹方程.
问题分析:直接法求解轨迹方程的基本步骤是:建系、设点、列式、化简、说明.其中建系、设点是描述轨迹问题的必然之路.此题若以AB为x轴、AB的中垂线为y轴建立直角坐标系,可以化简运算,降低解题难度.
代数求解:以AB为x轴,AB的中垂线为y轴,建立平面直角坐标系(图略),则点A(-2,0),点B(2,0).设动点P(x,y).由 条 件可知:,化简得P点的轨迹方程为:
几何优化:代数法直接的求解过程很难让学生完全建立起对此类问题轨迹为圆的认知,而且圆心的偏移也让学生想象起来有一定的难度.利用几何画板动态演示,则很形象地说明P点的轨迹为圆.
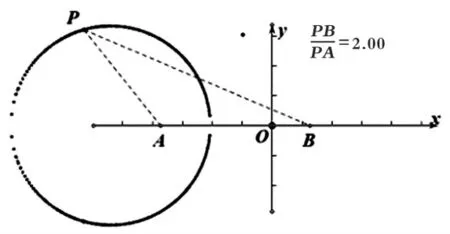
图1
变式1:坐标系中已知线段AB的端点坐标分别为:A(-1,-1),B(2,2),若动点P满足,求动点P的轨迹方程.
问题分析:此问题已经在具体的坐标系中给定特定的点,难点在于这两点都不在坐标轴上,所以求得圆的方程会更具一般化.但仍然可以通过代数法进行求解,利用几何法进行优化[1].
代数求解 :设动点P(x,y).由条件可知 :3,化简,得P点的轨迹方程为:


图2
2.定义法
例2已知直线l∶y=k(x-4)与圆O:x2+y2=4相交于A、B两点,当k变动时,求AB中点P的轨迹方程.
问题分析:定义法是利用圆的定义,即到定点的距离等于定长,判断出轨迹为圆.然后利用几何关系进行代数求解.本题不难发现OP、CP、OC三边长满足勾股定理,易得圆的方程.
代数求解:直线l∶y=k(x-4)恒过点C(4,0),设中点P的坐标为(x,y),连接OP,易知OP⊥AB,则有OP2+CP2=OC2,即x2+y2+(x-4)2+y2=16,化简得:(x-2)2+y2=4,再由中点P在圆O内部,可知x2+y2<4.
几何优化:一些学生对此类问题的几何特征挖掘较为困难,原因是对于动态的问题在脑海中把握不变的本质[3].本题若采用几何画板演示,学生不难发现当k变动时,PD的长度保持不变(直角三角形斜边上的中线始终是斜边的一半),所以P点的轨迹必然为圆.容易看到,P点在圆O外部时,没有轨迹.
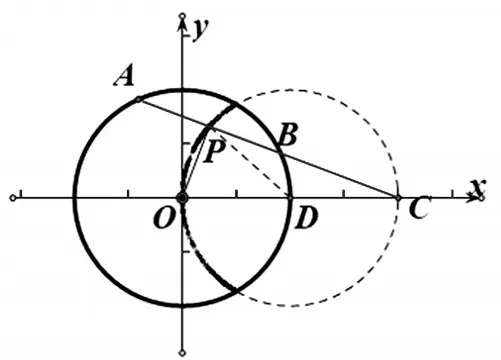
图3
变式2:已知线段AB的长度为4,且端点A、B分别在x轴、y轴上移动,求线段AB的中点P的轨迹方程.
问题分析:本题的难点仍然在于对P点的轨迹为圆的挖掘.在代数求解过程中,则可以利用两点间的中点公式以及距离公式进行转化求解.
代数求解:设P点的坐标为(x,y),A点的坐标为(x0,0),B点的坐标为(0,y0).由|AB|=4得,化简得:由中点坐标公式可得:x=2x0,y=2y0.代入得P点轨迹为:x2+y2=4.
几何优化:采用几何画板将更为直观地看到:除线段AB同在x轴、y轴两种特殊情况外,A、B点均能和坐标圆点O构成直角三角形.0P作为斜边上的中线,始终保持长度为2,轨迹方程为x2+y2=4.当A、B同在x轴或y轴上时,P点坐标仍满足上式.

图4
3.相关点法
例3 已知线段AB的中点P(2,2),点A在圆O:x2+y2=4上移动,求线段AB的端点B的轨迹方程.
问题分析:此类问题是线段的中点确定,一个端点随着圆上的另一个端点移动.采用代数法求解应寻找相关点之间的联系,从而建立方程.此题中主要用到的是中点公式.
求解过程:设P点的坐标为(x,y),A点的坐标为(x0,y0),由中点坐标公式可知:x0=4-x,y0=4-y.代入圆的方程可得:(4-x)2+(4-y)2=4.化简可得:(x-4)2+(y-4)2=4.
优化策略:本题中相关点的运动,用几何画板进行动态演示,可以形象地展示出B点的轨迹为圆.该圆的方程也可以用特殊位置求解.即连接OB两点,根据图象不难求得轨迹圆的圆心为(4,4),半径为2.
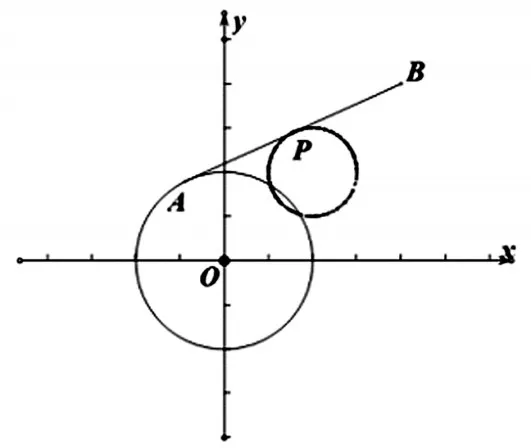
图5
变式3:已知线段AB的端点B(4,4),点A在圆O:x2+y2=4上移动,求线段AB中点P的轨迹方程.
问题分析:本题改变条件,变为线段的一个端点确定,另一个端点在圆上运动,求随之引起的中点变化轨迹.仍然可以利用上述代数方法求解.
求解过程:设P点的坐标为(x,y),A点的坐标为(x0,y0),由中点坐标公式可知:x0=2x-4,y0=2y-4.代入圆的方程可得:(2x-4)2+(2y-4)2=4.化简可得:(x-2)2+(y-2)2=1.
优化策略:本题中相关点的运动,用几何画板进行动态演示,可以形象地展示出P点的轨迹为圆.该圆的方程也可以用特殊位置求解.即连接OB两点,根据图象不难求得轨迹圆的圆心为(2,2),半径为1.

图6
总之,圆的轨迹问题是高中数学中的重要内容,是综合性较强的问题,主要考查学生动态思维能力和图象感知能力.在此类问题的教学中,教师应避免灌输式地讲授,直接告诉学生“死”的规律和方法,而应该用动态演示的方法,让学生直观感知到知识内在的原理.通过几何画板的演示,可以较为容易地实现培养学生动态思维能力的目标,从而让学生提炼方法,把握运动本质,真正做到举一反三.

