关于圆切线的考向例析与探究思考

顾亚平

[摘  要] 圓切线是初中几何的重点，其性质、定理也是常考知识. 分析近几年的中考试题会发现，中考试题题型灵活，考查知识点多，综合性强，对学生的知识综合运用能力及思维能力有着较高的要求，所以结合考查方法对圆切线内容加以探究有着重要的意义. 文章结合实例对几个圆切线常见考查视角进行探讨，提出相应的建议.

[关键词] 圆切线;考向;性质;判定;三角形;翻折

圆是初中数学的核心图形，含有众多的考点，其中与圆切线相关的定理既是中考考查的重点，又是几何问题突破的关键. 而切线的考查方向及视角较为多样，下面结合实例对圆切线的考向进行探究.

关于圆切线的考向举例

圆切线的概念相对容易理解，但切线背后隐含了几何数量关系和位置关系，由切线所构成的直角更是特殊图形形成的基础. 中考对圆切线的考向较多，其中有如下几个重要方向：圆切线的计算及证明、三角形的内切圆、切线性质的推理与计算.

1. 切线的计算及证明

论证圆切线的关系有多种考查方式，通常有如下两个方向：一是从动点角度命题，直接考证圆运动过程中与直线的交点;二是从量的角度出发，偏重与圆相切时隐含的数量关系. 但无论如何命题，考查切线的判定定理这一本质是不变的，只需要充分结合切线的判定方法来构建思路即可.

例1  （2019年遂宁中考卷）如图1，△ABC内接于⊙O，直径AD交BC于点E，延长AD至点F，使DF=2OD，连接FC并延长交过点A的切线于点G，且满足AG∥BC，连接OC. 若cos∠BAC= ，BC=6.

（1）求证：∠COD=∠BAC;

（2）求⊙O的半径OC的长;

（3）求证：CF是⊙O的切线.

解析  此处主要剖析第（3）问，证明OC⊥GF或∠OCF=90°即可. 直接进行角度推导存在一定的难度，可在图形中提取相似三角形. 已知Rt△COE，若能证明△COE与△FOC相似，即可直接推导出∠OCF=∠OEC=90°，即CF是⊙O的切线，过程如下.

因为DF=2OD，所以OF=3OD=3OC. 所以 = = . 又∠COE=∠FOC，所以△COE∽△FOC. 由相似三角形的性质可得∠OCF=∠OEC=90°. 所以CF是⊙O的切线.

评析  切线的计算及证明，实质就是考查圆相切关系的证明方法. 相切意味着垂直，故可通过角度推导和三角形边长关系分析来加以论证. 该考查方向还可以综合三角形相似、勾股定理、三角形全等等知识.

2. 三角形的内切圆

三角形的内切圆是考查圆切线的另一特殊考向. 三角形的内切圆与三角形的三条边均相切，此时的圆心为三角形的内心. 分析图像可知，圆心到三角形三边的距离相等，深入分析可将其与角平分线的性质相关联，故该考向主要考查三角形内切圆的性质、角平分线的性质等.

例2  （2019年兴化期末卷）如图2，△ABC的周长为20 cm，BC=6 cm，△ABC的内切圆为⊙O，MN是⊙O的切线，MN与AB相交于点M，与CA相交于点N，则△AMN的周长为______.

解析  题干设定△ABC的内切圆为⊙O，则圆心O到△ABC三条边的距离相等. 同时可在图形中提取角平分线，获得相应的全等三角形，进而进行等线段转化，完成△AMN的周长求解，具体如下.

过点O分别作AB，BC，AC和MN的垂线，垂足分别为E，F，D，G，连接BO. 分析可知OF=OE，显然BO为∠FBE的平分线，进而可证△FBO≌△EBO. 由全等性质可得BE=BF. 同理可得CF=CD，DN=NG，EM=GM，AD=AE. 因为△ABC的周长为20 cm，BC=6 cm，所以可推得AE=AD=4. 所以△AMN的周长=AM+AN+MN=AE+AD=8.

评析  三角形的内切圆问题涉及角平分线、三角形全等等知识，利用其中的等角和全等图形可完成等线段转化，因此，其中的周长问题实则就是等线段转化问题. 可见，理解考向的本质是解题突破的关键.

3. 切线性质的推理与计算

切线性质的推理与计算是常见的考查方向，虽考点一般，但其中涉及的知识点较多，通常融合了三角函数，圆周角、圆心角、弧、弦之间的关系，深刻理解切线的性质，充分利用其性质进行关联转化是问题突破的关键.

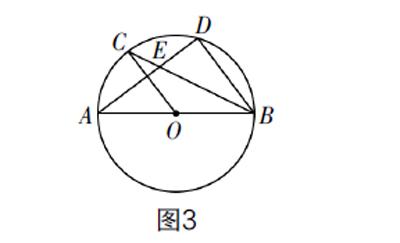
例3  （2019年成都中考卷）如图3，AB是⊙O的直径，C，D为⊙O上的两点，OC∥BD，弦AD，BC相交于点E.

（1）求证： = ;

（2）若CE=1，EB=3，求⊙O的半径;

（3）在（2）的条件下，过点C作⊙O的切线，交BA的延长线于点P，过点P作PQ∥CB交⊙O于F，Q两点（点F在线段PQ上），求PQ的长.

解析  上述与圆相关的问题涉及证明弧长相等、求圆半径长和求线段长三大问题，分析时需要充分利用圆的性质.

（1）等弧所对的圆周角相等，只需证明∠OBC=∠CBD即可. 由于OC=OB，所以∠OBC=∠OCB. 又OC∥BD，所以∠OCB=∠CBD. 所以∠OBC=∠CBD. 所以 = .

（2）求⊙O的半径可先求直径AB，连接AC，则∠ACB=90°. 分析可知BC=4，△ACE∽△BCA，由相似性质可得 = ，则AC2=CB·CE=4. 所以AC=2. 在Rt△ACB中，由勾股定理可得AB= =2 ，所以⊙O的半径为 .

（3）根据题干信息作图，再过点O作PQ的垂线，垂足为H，如图4. 因为PC是⊙O的切线，所以∠PCO=90°. 所以∠PCA=∠BCO=∠CBO. 又∠CPB=∠CPA，所以△APC∽△CPB. 由相似性质可得PC=2PA，PC2=PA·PB，所以PA= ，PO= . 分析可证△PHO∽△BCA，由相似性质可得 = = ，可解得PH= ，OH= ，所以HQ= = . 所以PQ=PH+HQ= .

评析 上述求证弧长相等及求线段长，考查了切线性质等与圆相关的知识，其中相似三角形的性质、勾股定理是本题思路构建的关键. 因此，对于圆切线的综合性问题，应关注复合图形的特点，充分利用特殊图形及特殊关系来进行线段、角度的转化.

4. 几何翻折与圆切线

几何翻折是初中几何的重点内容，圆切线知识也可与几何翻折联合起来考查. 解析时需要充分理解图形翻折的过程，利用翻折过程中“变”与“不变”的量、圆的切线性质来剖析图形、构建思路.

例4  如图5，AB为⊙O的直径，点C在⊙O上，现将 沿着直线BC进行翻折，恰好 的中点D落在圆心O处. 连接OC，CD，BD，过点C的切线与BA的延长线交于点P，连接AD，于PB的另外一侧作∠MPB=∠ADC.

（1）分析PM与⊙O的位置关系，并简述理由;

（2）若PC= ，试求四边形OCDB的面积.

解析  （1）连接DO并延长交PM于点E. 根据折叠性质可得OC=DC，BO=BD，又BD=CD，所以四边形OBDC为菱形. 由菱形性质可得OD⊥BC. 又OD=OC=OB，所以△OCD和△OBD均为等边三角形. 所以∠COP=∠EOP=60°. 通过证明PM∥BC得到OE⊥PM，进一步推得OE= OP，根据切线的性质可得OC⊥PC，且有OC= OP，故OC=OE，从而可判定PM是⊙O的切线.

（2）在Rt△OPC中，OC= PC=1，所以四边形OCDB的面积=2S =2× ×12= .

评析  本题的翻折背景中涉及圆切线的性质，由切线中的垂直关系来构造图形是突破的关键. 综合考查折叠、圆切线性质、圆周角定理也是中考的重点考向，在复习阶段应重视对几何知识的整合，提升解题的综合能力.

关于圆切线考向的学习建议

1. 挖掘定理，串联定理

圆切线的判定、性质定理虽内容较为简单，但在学习时应深入挖掘定理内涵，理解其中的知识原理，如圆与线段相切中隐含着如下特殊关系：数量关系——圆半径与圆心到切线的距离相等，垂直关系——切线和圆心与切点的连线垂直. 而对于切线判定定理，则应把握其中的条件，包括公共点、垂直关系等. 定理之间并不是独立存在的，学习几何定理时还应联系前后知识加以串联，关注圆切线与角平分线性质、勾股定理、圆周角定理等定理之间的联系，建立完整的定理体系，为后续综合问题的突破奠定基础.

2. 考向综合，技能提升

圆的性质定理是中考的重点，上述例子探讨了圆切线性质定理的主要考向，其中包括基本的相切论证、线长推断，也涉及综合性的三角形与圆内切、翻折与圆切线. 从考查内容来看，涉及相似性质、全等性质、勾股定理、角平分线性质、三角函数、翻折特性等，这些内容是平面几何的核心，因此对于该部分的学习需要立足基础，综合知识，发展思维. 同时，圆切线问题的解决离不开辅助线，合理添加辅助线有助于挖掘圆内特性，有利于解题思路的构建，因此应掌握圆切线问题中辅助线添加的技巧，增强作图能力，促进综合素养的提升.

总之，圆切线的考向较多，充分理解定理、把握知识关联、关注问题类型、总结解题技巧是该内容学习的关键. 另外，圆切线问题的求解中渗透着数学思想，合理利用数形结合、模型思想、转化思想可提高解题效率，故应重视思想方法的学习，综合提升解題能力.