新线搜索条件下的Dai-Yuan型共轭梯度法

曹尹平，周光辉

（淮北师范大学 数学科学学院，安徽 淮北 235000）

0 引言

考虑大规模无约束优化问题，即min{f(x)|x∈Rn}，其中f(x):Rn→R 是一阶连续的可微函数. 在求解上述问题时，共轭梯度法凭借其计算简便，收敛速度快，存储数据少且具有二次终止性等优点，被广泛应用于处理诸多最优化问题，也是目前较为常用的有效方法之一. 其迭代形式为：

其中：gk=∇f(xk)为目标函数f的梯度函数，αk为步长因子，dk为搜索方向，βk为参数标量. 由式（1）可知，影响共轭梯度法的2个重要因素就是搜索方向dk与步长因子αk，而搜索方向dk的改变取决于参数标量βk的变化. 自从1964年Fletcher等提出非线性共轭梯度法之后，经历数十年的发展，诸多专家学者提出4种经典共轭梯度法，在搜索方向dk上改变其参数标量βk的多种变化形式［1-5］：

其中：yk-1=(gk-gk-1)，‖· ‖ 表示为欧几里得范数. 当目标函数f是严格凸二次函数且采用精确线搜索确定步长因子αk时，上述经典共轭梯度法可以相互等价. 但由于精确线搜索要求过于严格，计算量较大，且部分算法无法到达理想效果. 因此在实际应用中常常采用非精确线搜索确定步长因子αk，其中较为常用的非精确线搜索有如下几种：强（弱）Wolfe 线搜索［6-7］，Armijo 线搜索［8］，Grippo-Lucidi 线搜索［9］和Goldstein线搜索［10-11］等. 然而算法在考虑非精确线搜索的时候，往往需要考虑如下2个关键问题：1.非精确线搜索准则所确立的步长因子αk是否存在；2.采用非精确线搜索准则运算的共轭梯度法是否具有全局收敛性. 在实际的运算过程中，每种线搜索都有其独特的优点与不足，步长因子αk的确定需要一定的运算时间，所以线搜索的选择会对算法的运算效率有所影响. 因此线搜索的选取也是判定算法优劣的重要一步.

2017年，Yuan等［12］提出一种新型非精确线搜索（modified weak Wolfe-Powell line search，简称MWWP型线搜索），MWWP型线搜索形式如下：

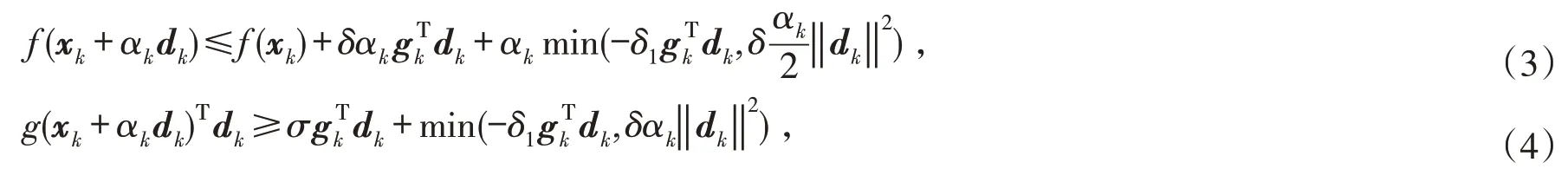
基于文献［12］提供的一种新型线搜索，本文将新型线搜索与Dai-Yuan型共轭梯度法结合，构建新算法并证明其全局收敛性. 与其他非精确线搜索进行数值实验对比，说明新型线搜索条件的Dai-Yuan 型共轭梯度法在求解无约束最优化问题时是有效的.

1 新线搜索下的Dai-Yuan共轭梯度法

基于MWWP型线搜索（3）和（4），构造算法框架如下：

算法1

步骤 1 给定初值.且当k=1 时d1=-g1. 如果‖gk‖≤ε，则停止.

步骤2 采用MWWP线搜索（3）和（4），计算步长αk.

步骤3 令xk+1=xk+αkdk，如果‖gk+1‖≤ε，则停止.

步骤4 利用βkDY与dk=-gk+βkdk-1迭代公式，计算下降方向.

步骤5 令k=k+1，进入循环返回步骤2.

为证明新型共轭梯度法的全局收敛性，需要下列假设.

假设（H1）目标函数f(x)在水平集Ω={x∈ Rn|f(x)≤f(x1)}上有下界，其中x1为初始点.

（H2）目标函数f(x)在水平集Ω的某一领域N内连续可微，梯度函数gk=∇f(xk). 满足Lipschitz 条件，即存在常数L>0 使‖g(x)-g(y) ‖≤L‖x-y‖,∀x,y∈N.

2 全局收敛性

Yuan等［12］提出MWWP型线搜索具有以下2种形式：

由于形式②中的δ1的取值由δ的取值范围所决定，所以一般情况下不具备全局收敛性，因此讨论MWWP线搜索在形式①的条件算法1的全局收敛性.

引理1序列{xk,αk,dk,gk}均由算法1 产生，且在满足MWWP 线搜索满足形式①的条件下，即成立，则关系式对于任意k都成立.

证明当k=1时，d1=-g1，则成立

假设当n=k-1时，有成立，则当n=k时有：

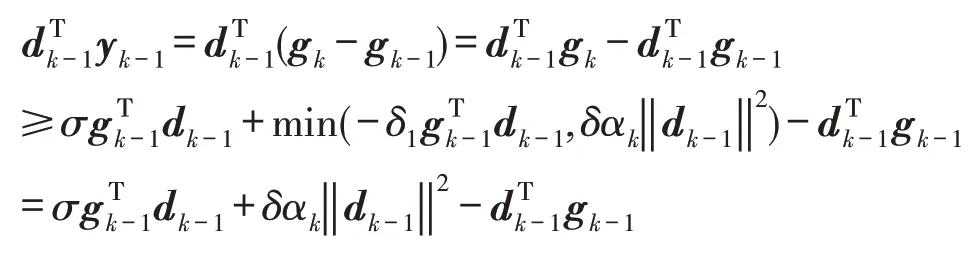
再由Dai-Yuan公式可知

由此可知，搜索方向是充分下降的.

引理2考虑算法1满足假设与引理1，序列{xk,αk,dk,gk}均由算法1产生，且MWWP线搜索满足形式①，由此可得

证明由假设（H1），f(xk+αkdk) 与f(xk) 有下界，且δ1<δ和成立. 如果α→∞，则成立.

再由上述假设与MWWP线搜索结合可得

对上述不等式进行求和得

再由假设（H2）与MWWP线搜索形式①条件有

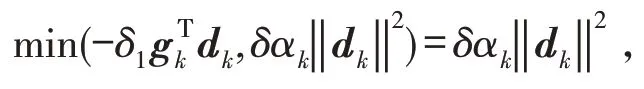
可得

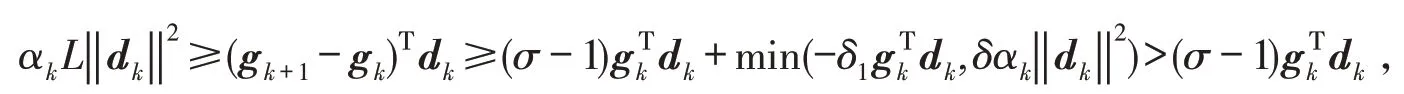
定理1考虑算法1 满足假设与引理1 与2，序列{xk,αk,dk,gk}均由算法1 产生，且MWWP 线搜索满足形式①，则或者gk=0 对于某个k成立，或者

证明若gk=0 对于某个k成立，则xk为点列的稳定点，定理恒成立. 否则，采用反正法.

假设定理不成立，则 ‖gk‖>0，对于任意k都成立. 设常数c，‖gk‖>0，∀k，由搜索方向迭代公式对上式变形得再两端取模平方，移项得：

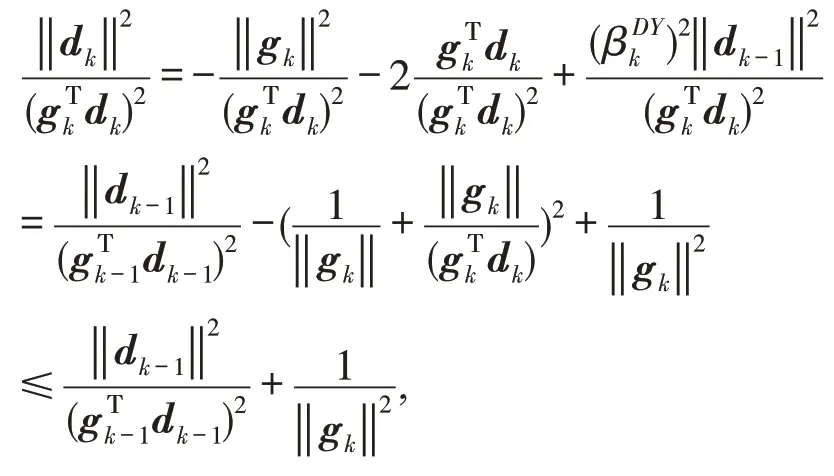
如果定理不成立，则存在常数c>0 使得‖gk‖>c对于所有k. 将其代入上述不等式中可得由此可知而上述求和与引理2中式（5）相矛盾. 由此可知假设不成立，定理成立.

3 数值实验

为检测算法的实际数值结果，对于常用的无约束测试函数集文献［14］中的算例进行模拟测试，并且与经典Dai-Yuan 型共轭梯度法进行数值比较. 经典算法将采用标准Wolfe 线搜索准则进行测试，算法1采用MWWP 线搜索进行测试. 算法的测试环境在Matlab 7.0，Win 7.0 操作系统，Intel（R）Core（TM）I5-3210M CPU 2.50GHz 4.00GB 内存下进行的. 其中算法1 中MWWP 线搜索参数选取如下：δ=0.49 ，δ1=0.24，σ=0.67.经典算法中Wolfe线搜索参数选取如下：δ=0.49，σ=0.67，ε=10-5，算法终止的条件为‖gk‖<ε或迭代次数超过1 000. 当终止条件是因为迭代次数超过1 000时，则认为该算法对此算例失效. 在实验中，对算法1与经典Dai-Yuan型算法分别在100维，1 000维和2 000维3种维数下，对函数进行测试比对. 测试函数见表1，将数值结果绘制成Dolan 性能对比图［15］（见图1～图6），其中Algorithm 1所代表的就是算法1，DY-method所代表的就是经典Dai-Yuan型算法.

表1 测试函数

图1 100维迭代次数对比

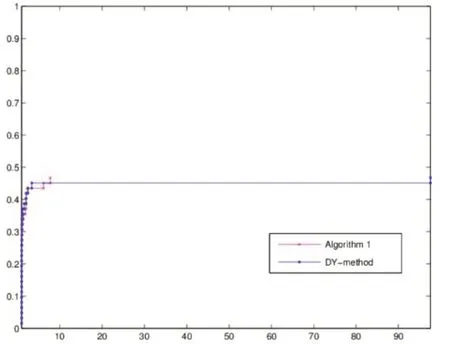
图2 100维迭代时间对比

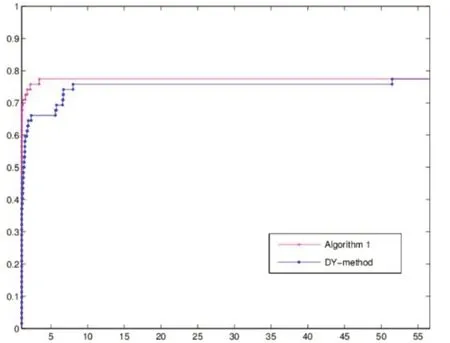
图3 1 000维迭代次数对比

图4 1 000维迭代时间对比

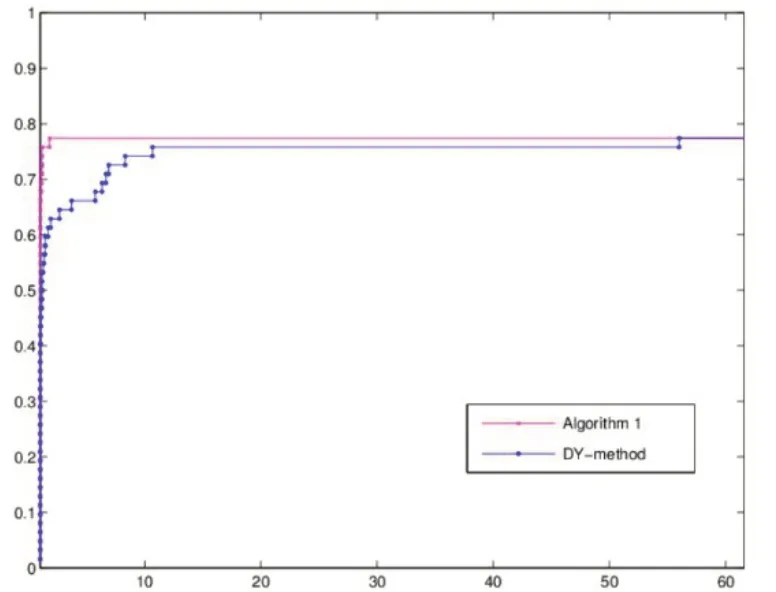
图5 2 000维迭代次数对比

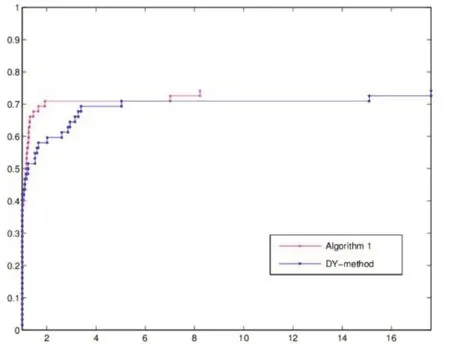
图6 2 000维迭代时间对比

4 数值结果分析

通过Dolan 性能图可以发现，采用MWWP 线搜索的Dai-Yuan 型共轭梯度法在迭代次数上是优于Wolfe线搜索下的Dai-Yuan型共轭梯度法的，而迭代时间的性能曲线在低维度时出现交叉，但是随着维度的上升，MWWP线搜索的优势趋于明显. 由此说明，采用MWWP线搜索的Dai-Yuan 型共轭梯度法适合解决较大规模的无约束优化问题.