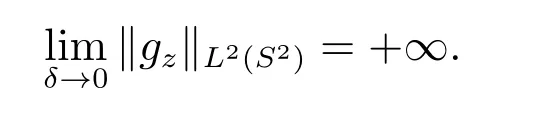基于单频数据重构散射障碍的新型线性采样方法
丁 濛
(北京信息科技大学计算机学院,北京 100101)
1 引言
散射及反散射的数学理论与计算一直是应用数学领域中的重要课题,其成果在地质勘探、无损探测、医学成像等领域都具有广泛的应用.散射研究入射波与介质的相互作用,而反散射则研究通过介质外部可测的波场探测其形状或内部属性.数学上,反散射主要研究解的唯一性、稳定性及设计高效、稳定的数值算法.目前,对该问题的研究,无论在唯一性方面还是在数值算法方面都取得了丰富的研究成果,例如基于远场数据反演散射障碍的唯一性定理[1-4]、迭代优化型算法[5-7]及采样型方法[8-11]等,详细内容可参考相关专著[12-14].
线性采样方法(LSM)是近年来反散射理论中一类非常流行的非迭代型重建算法,它由Colton 和Kirsch 于1996 年首先提出[9].其主要思想是考虑第一类算子方程
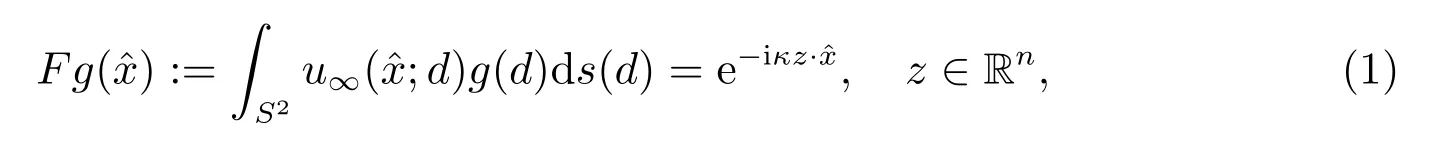
这里,F :L2(S2)→L2(S2)为定义在R3中单位球面S2上的远场算子,u∞为散射场的远场模式,它是定义在S2×S2上的解析函数,在实际中通常被认为是一个可观测量.针对方程(1),可证明如下定理.
定理1[9]若κ2>0 不是-Δ 算子的Dirichlet 特征值,则对任意的z ∈D, ε >0,存在函数gz,ε∈L2(S2),使得
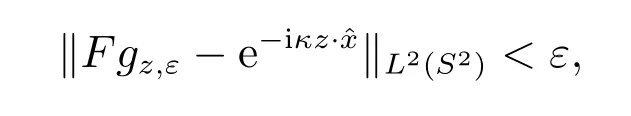
且
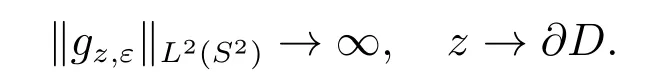

1) 不需要先验地知道障碍D 的物理性质;
2) 不需要数值求解正散射问题.
因此,近二十年来,LSM 被广泛应用于一般偏微分方程反问题中,如文献[15-17]等.然而,就像定理1 所描述的那样,传统的LSM 仅在κ2>0 不是区域D 上-Δ 的Dirichlet 特征值时有效.那么自然地会产生“当κ2是-Δ 的Dirichlet 特征值时,LSM 是否依然有效?”这个问题.为了解决这一问题,文献[18]首先借助修改边界积分方程积分核的方式给出了一个变种的第一类远场算子方程,并通过研究相应的远场算子的性质,证明了改良后的LSM 在每个固定的波数下都是有效的.然而这种方式很难推广到更为复杂的反散射问题中,例如半空间中障碍反散射问题、无界带状区域中障碍反散射问题等.
本文主要以Dirichlet 障碍为例,研究了一类反散射问题的数值计算方法,目的是在波数无任何先验信息下,发展一种快速有效的新型线性采样方法,并且使得该方法能够很容易推广到其他复杂情形.为此,本文在第2 节给出了散射问题的描述,并呈现了解的一些基本性质;然后,在第3 节给出了本文的主要结果及其证明,核心思想是通过引入带阻尼边界条件的辅助边值问题,把原问题转化为特殊入射波下的散射问题,从而可以建立起相应算子的单射及稠密性.
2 问题描述
令D 为R3中C2-光滑的有界区域,其边界为∂D.考虑平面波
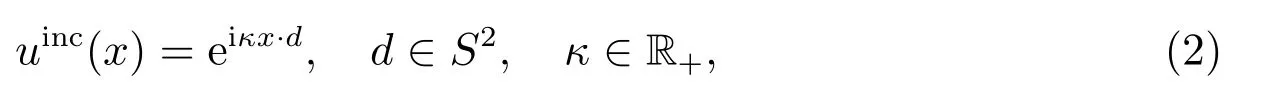
入射到障碍D,则其散射由Helmholtz 方程所描述
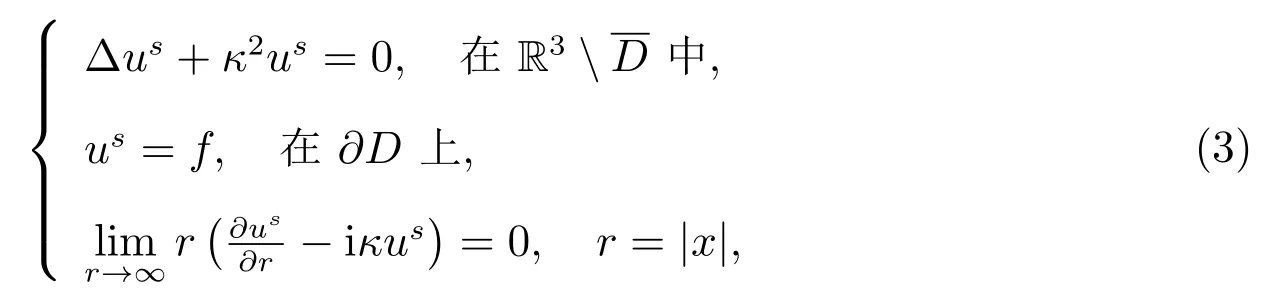
其中f =-uinc.(3)式中的第三个条件被称为Sommerfeld 辐射条件.
利用Green 公式及Sommerfeld 辐射条件,散射场us有如下渐近形式

定理2[14]对于f ∈H1/2(∂D),边值问题(3)有唯一解us且满足
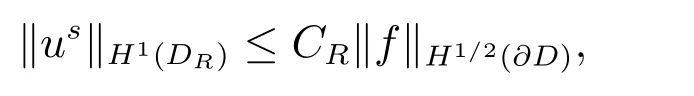
现在引入算子Lf := u∞.由定理2 可知,L 是H1/2(∂D)到L2(S2)上的有界线性算子.进一步地,关于L 也有如下性质.

3 主要结果及证明
本节将研究问题(3)的反散射问题,即通过测量远场模式u∞反演障碍D 的位置和形状,其目标是提出一类新型的线性采样方法,使得该方法在任意给定的波数下都是有效的,同时又易推广到其他情形.


令w :=us-ps,易验证w 满足如下问题
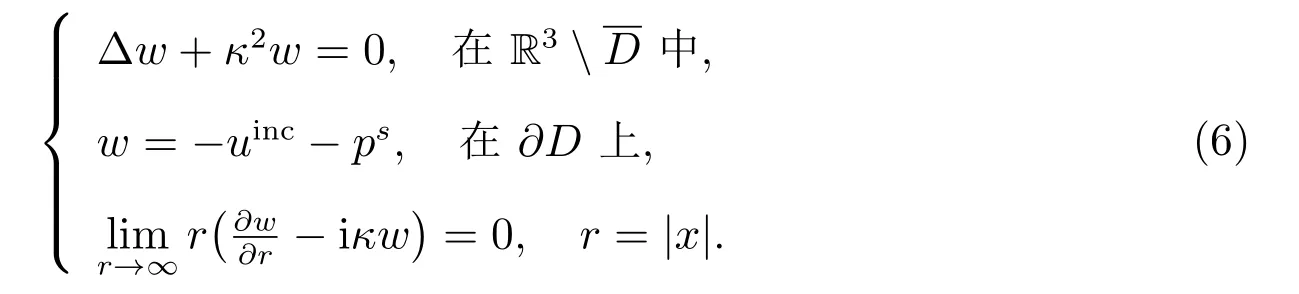
再令p:=uinc+ps及定义入射算子H :L2(S2)→H1/2(∂D):
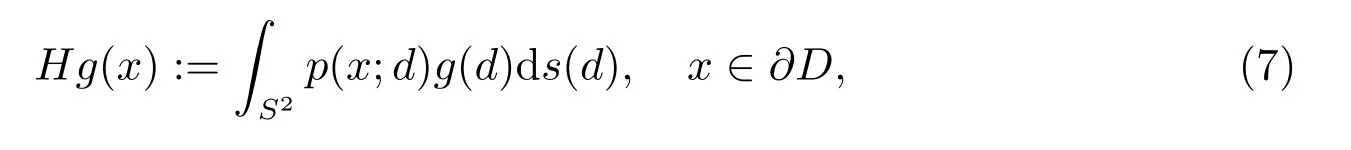
则可以证明如下结果.

证明 为了证明H 的单射,引入函数

若存在g ∈L2(S2)使得Hg =0,则U|∂D=0.再由p 与U 的定义可知,U 满足如下问题

利用Green 定理及Holmgren’s 唯一性定理易得,当x ∈R3Bδ(x*)时,U(x)=0.又因为p=uinc+ps,所以

由(8)式可知其左端和右端同时为0.若不然,不难发现(8)的右端满足Sommefeld 辐射条件,而左端不满足Sommefeld 辐射条件,这导致了矛盾.然后,利用唯一延拓原理及文献[13, 定理3.19]可得g =0.故H 为单射.
为了证明Range(H)在L2(S2)上的稠密性,根据泛函分析中的理论可知,这等价于证明H 的伴随算子H*: H-1/2(∂D) →L2(S2)是单射.为此,对于ψ ∈H-1/2(∂D),首先通过积分交换次序可得

其中H*定义为
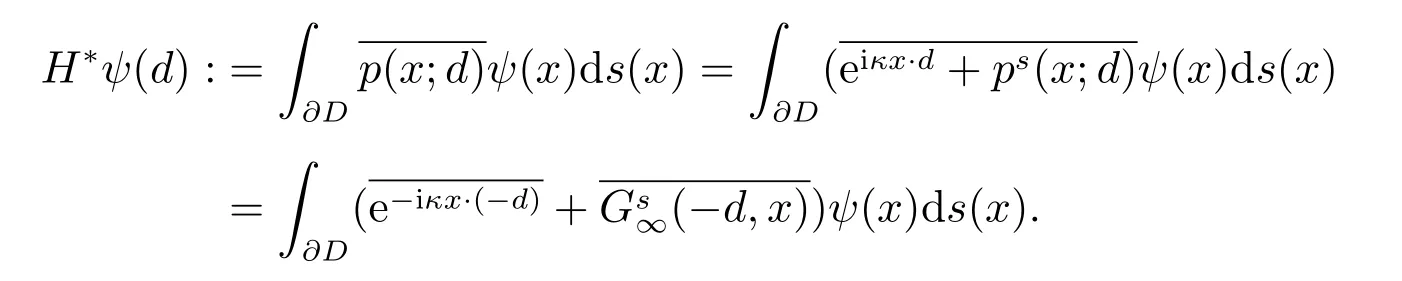
上式的推导中已经利用了(5)的解的混合交互关系
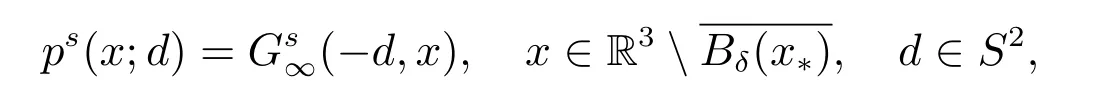
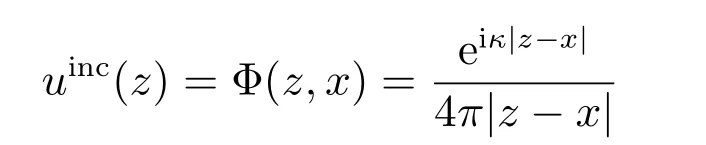
时,散射解ps:=Gs(z,x)对应的远场模式.
定义函数

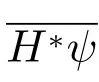

下一步,引入新的远场算子FM:L2(S2)→L2(S2):
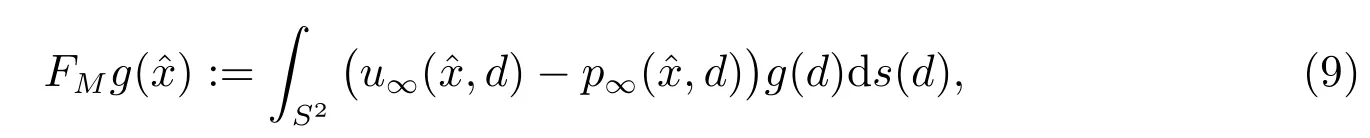
其中u∞与p∞分别对应于问题(3)和(5)中解的远场模式.那么,本文提出的新型采样方法主要基于求解第一类积分方程

针对方程(10),可以得出如下的主要结果.
定理3(i) 若z ∈D,对任意的ε >0,存在gz,ε∈L2(S2),满足
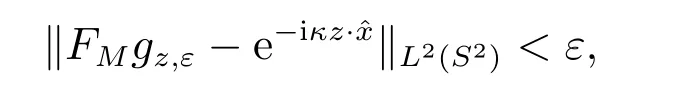
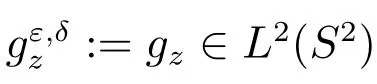
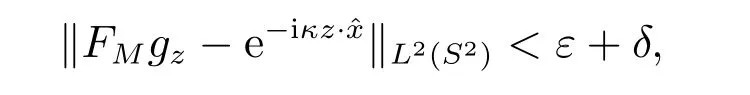
证明 为了证明(i),首先证明下面的充分必要条件

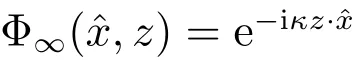
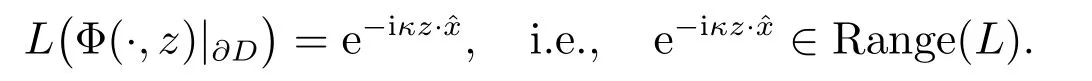
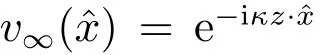
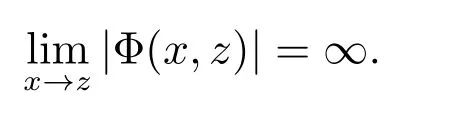
这矛盾于
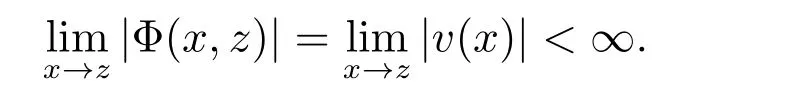
再若z ∈∂D,则

这也矛盾于

因此假设z /∈D 不成立,即z ∈D.故(11)式成立.
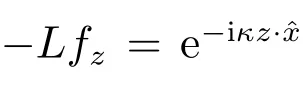

注意到,根据线性叠加原理得FM=-LH.这联合(12)及L 的有界性进一步得
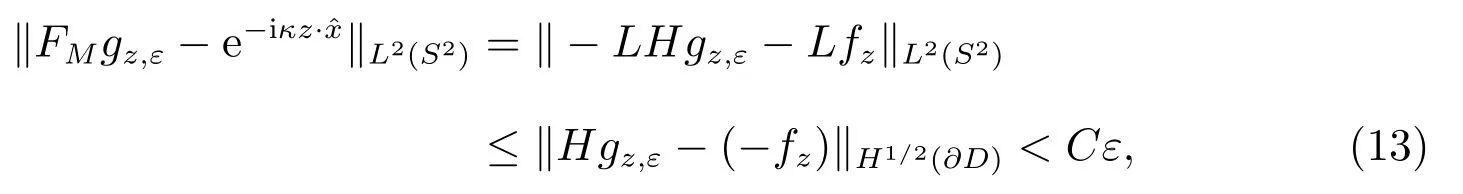
这里,C >0 是一个固定常数,仅依赖L 的范数.

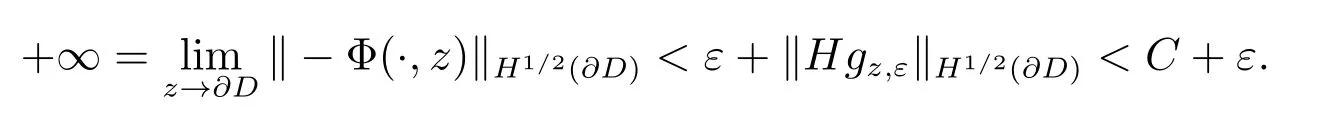
这是个矛盾.因此
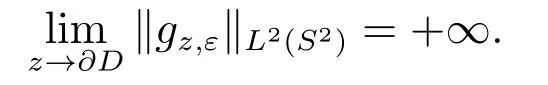
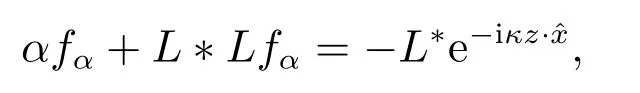
其解可表示为如下形式
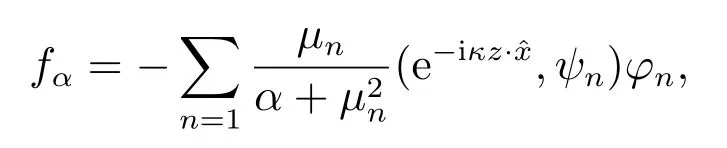
其中(μn,ψn,φn)为算子L 的奇异值系统.注意到,根据文献[12, 定理2.13],fα是相应的Tikhonov 泛函的极小值.因此,对于给定的δ >0,通过选择正则化参数α,下式成立
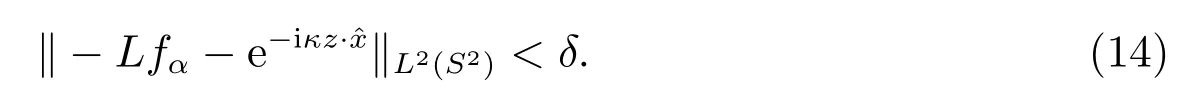
再利用Picard 定理,可得
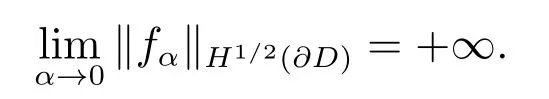
另一方面,由于Range(H) 在H1/2(∂D)中是稠密的(引理2),所以存在函数gz∈L2(S2),使得对于给定的ε >0,
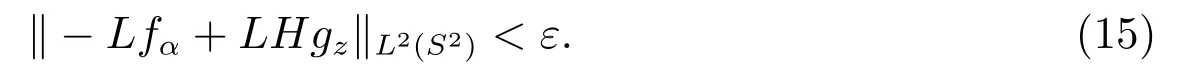
再联合(14)及(15)式可得

最后,类似于情形(i),容易证明