一种基于LS-WTLS的稳健平面拟合方法

欧江霞，邓雄文，蔡茂欣，邱 敏

(广州市地质调查院，广州 510440)

引 言

平面拟合可用于建(构)筑物倾斜监测、边坡变形监测、隧道断面监测、3-D激光扫描点云滤波[1-2]等工程领域，其精度会对变形分析、点云滤波和3-D建模效果产生重要影响。鉴此，有必要在传统拟合方法基础上，顾及误差数据比例及其大小对拟合结果产生的影响，构造最佳平面拟合方法，提高所求平面参量的准确度。

目前，常用平面拟合方法包括传统最小二乘(least squares，LS)法、总体最小二乘(total least squares，TLS)法[3-5]、混合总体最小二乘(mixed TLS,MTLS)法[6]等，以上方法均将各点当做独立等精度观测值处理，由于受观测环境、系统误差等因素影响，观测数据3-D坐标x,y,z3个方向上均含有误差且各点点位精度均不相同，若采用上述方法进行平面拟合，所得参量解并非平面参量的最或然值。因此，国内外学者在加权总体最小二乘(weighted total least squares，WTLS)模型[7-8]基础上，顾及各点点位精度差异性，结合基于方差-协方差膨胀的抗差估计，提出了加权总体最小二乘平面拟合算法，同时对抗差估计中的权因子函数进行了深入探讨，构造了多种定权准则及与其相对应的平面拟合方法[9-11]，一定程度上提高了平面参量解的准确度。但对于各WTLS法，其已虽将平面模型中的常数项当做无需修正项对待，但实际拟合过程中，常数项因受点位拟合权值影响，准确度较低。

本文中提出了一种基于LS-WTLS混合解算平面参量的方法，该方法将平面参量划分为含误差与不含误差(常数项)两部分，综合利用WTLS法、LS法对这两部分参量进行解算，即顾及到各点点位精度，选用WTLS模型，在此基础上，以稳健估计中的IGGⅢ(由中国科学院测量与地球物理研究所(Institute of Geodesy & Geophysics,IGG)提出的一种抗差估计方法,IGGⅢ是第3种衍生方法)方案权因子为定权函数[11-15]，在参量迭代解算过程中确定各点拟合权重，并自适应的对拟合权阵进行合理修正，提高误差项参量解算精度，与此同时，又以三倍权因子中误差为阈值剔除粗差数据，利用LS法求取常数项，有效抵抗点位拟合权值对常数项解算的影响。

1 基于LS-WTLS的稳健平面拟合方法

1.1 顾及双矩阵误差的平面方程混合模型

设平面方程为：

Z(i)=aX(i)+bY(i)+c,(i=1,2,…,n)

(1)

式中，a,b,c为待求平面参量，定义a,b为误差项参量，c为常数项参量。下标(i)表示迭代。顾及观测向量误差与系数矩阵误差的平面方程变量误差模型为：

Z-e=(A1+EA1)ξ1+A2ξ2

(2)

式中，Z为含有随机误差e矩阵的n×1维观测向量；A=[A1,A2]为系数矩阵，A1为误差项系数矩阵，A2为常数项系数矩阵；ξ=[ξ1,ξ2]T为代估参量矩阵，ξ1为误差参量矩阵，ξ2为常数项矩阵：

(3)

式中，v表示计算值与实测值之差。在满足‖(ΔA1,ΔZ)‖F=min的约束条件下(‖·‖F为F范数)，可求得ξ的值。

1.2 基于LS-WTLS的平面参量解算及精度评定

参照WTLS模型迭代解算方法，可将(2)式可改写成如下形式：

Z-e=Aξ(i)+A(i)δξ-Eξ(i)

(4)

式中，A(i)=A-E(i)，δξ=ξ(i+1)-ξ(i)，根据(4)式构造拉格朗日目标函数：

Aξ(i)-A(i)δξ-e+(ξ(i)T⊗I)e]

(5)

式中，λ为n×1维拉格朗日乘数,I是单位矩阵，T表转置。通过对(5)式求导、求极值即可计算出λ及参量ξ(i)的代估值。

(6)

(7)

式中，QZ,QA,Q0分别为PZ,PA,P0的广义逆。

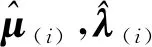
(8)

(9)

(5)利用(10)式计算各残差V(i):

(10)

(6)根据V(i)及IGGⅢ方案(见(11)式)计算权因子ω(i)，令P(i)=P(i)ω(i)，之后根据准则重新设定权阵PA(i+1),PZ(i+1):

(11)

式中，V(i)为残差，σ为中误差，k0=1.0～1.5，k1=2.5～3.0，本文中取k0=1.5,k1=2.5。

(12)

(13)

式中，d(i)为点至拟合平面的距离。

2 算例分析

为对本文中所构建平面拟合方法的适用性及优越性进行验证，分别利用其对模拟平面数据、实测平面数据进行拟合。

2.1 模拟数据

设要拟合的平面方程为Z=3X+4Y+5，依次抽取4组观测数据，并分别按照0%,5%,10%,20%的比例加入粗差(大小为3σ0～5σ0，σ0为每组观测数据的中误差)，每个观测数据中，X,Y分别为[0,1000],[0,2000]区间内的随机整数，相应的Z为[5,11005]区间内的随机整数，同时在模拟数据中加入随机误差e，且随机误差e服从均值为0、标准差为σ2I的正态分布(σ=0.3，I为单位阵)。

Table 1 Plane parameters and fitting precision of simulated data

分别利用LS法、TLS法(奇异值分解(singular value deeoniposition,SVD))、LS-TLS法、IGGⅢ-LS-TLS法[5]、LS-WTLS混合法(本文中算法)对上述4组观测数据进行拟合实验，各方法计算得到的平面参量及精度评定指标如表1所示。

表1中，当粗差比例为0%时，各方法所得参量解非常接近实际参量值，单位拟合中误差与平面拟合精度较小，由此说明各方法的拟合效果均比较好，仅由于数据取位原因导致各方法所得参量值与实际参量值之间存在一定偏差。

当粗差比例由5%递增到20%时，各方法所得参量解与实际参量值的偏差越来越大，单位权中误差与平面拟合精度呈递增趋势，由此说明，拟合效果随粗差的增加而变差。其中，LS法受粗差影响，拟合效果较粗差比例为0%时明显下降；TLS法过多顾及到系数矩阵不含误差部分，整体拟合效果最差；LS-TLS法虽顾及平面参量的常数项不含误差，对两部分参量进行独立解算，但其未考虑到各观测值精度差异，因此拟合效果不稳定；IGGⅢ-LS-TLS法综合考虑了含误差参量与常数项的区别，对其进行了独立解算，同时根据各观测值的精度，确定其参量平面拟合的权重，因此获得了较好的拟合效果；LS-WTLS混合法在IGGⅢ-LS-TLS法的基础上，引入加权总体最小二乘模型，以拟合残差为依据、IGGⅢ方案为定权准则，在含误差参量迭代解算过程中，其可自适应地修正观测向量权阵及系数矩阵权阵，以获取最能合理反映各观测值精度的权值，同时又以三倍权因子中误差为阈值，剔除观测数据中的异常数据，再利用LS法计算得到常数项的值，最终，通过有限次的迭代计算，获得了最为可靠参量解，该方法较好抵抗了粗差干扰，各项拟合指标均优于其它算法，拟合精度最高。

2.2 实测数据

表2中[16]，X为坝体温度实测值、Y为水位压力实测值、Z为大坝水平位移实测值(X,Y,Z无具体单位),3个向量构成Z=aX+bY+c的平面关系。再次利用LS法、TLS法(奇异值分解(SVD))、LS-TLS法、IGGⅢ-LS-TLS法、LS-WTLS混合法(本文中算法)对表2中的实测数据进行拟合实验，所得平面参量及精度评定指标如表3所示。

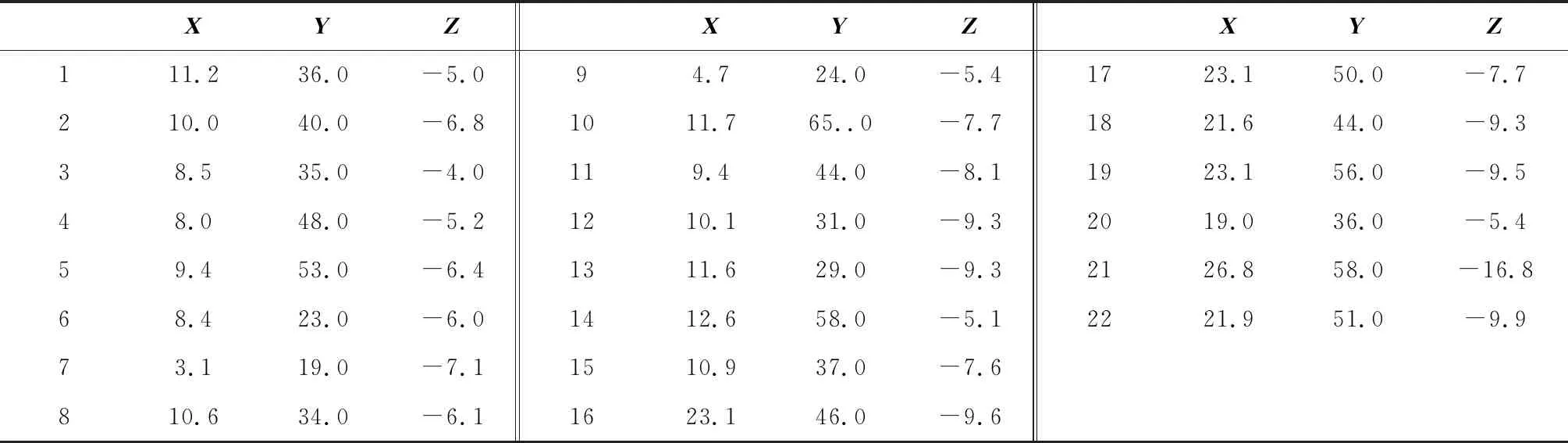
Table 2 Observed data of plane

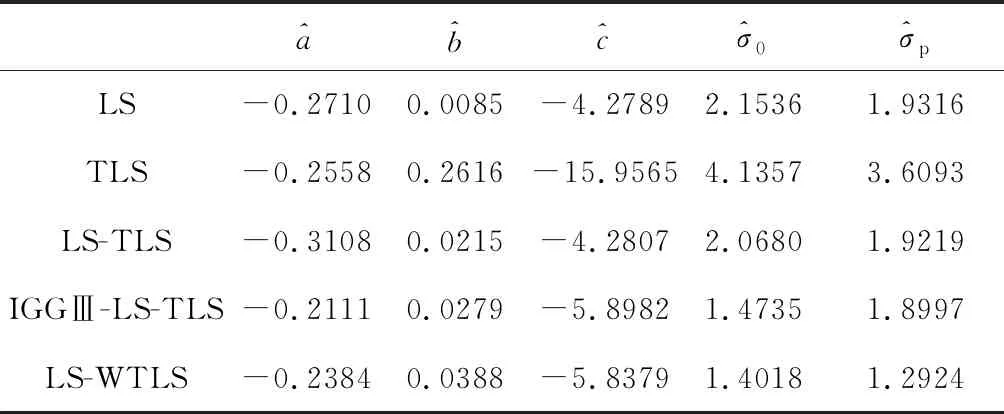
Table 3 Plane parameters and fitting precision of observed data

3 结 论

提出了一种对平面含误差与不含误差(常数项)两部分参量进行独立解算的LS-WTLS平面拟合方法。在误差项参量解算过程中，顾及平面数据各点精度存在差异，本文中依据稳健估计中各权函数特点及其适用范围，选用IGGⅢ方案对加权总体最小二乘平面拟合方法进行改进，其可在模型参量解算过程中，通过计算点与平面模型的相关关系，自适应地调整各点拟合权值，优化拟合权阵；对于常数项，先以三倍权因子中误差为阈值剔除观测数据中的粗差，再利用LS法进行解算。模拟平面数据及实测平面数据的拟合实例表明，该方法具备较好的可行性及优越性，利用该方法拟合得到的平面参量解可靠性更高。

基于LS-WTLS的稳健平面拟合方法较最小二乘法、总体最小二乘法、混合总体最小二乘法更为稳健，但在解算过程中，当数据量过大时，由于权值的自适应修正过程较为复杂，迭代计算较为繁琐，解算所需时间较多，如何提高解算效率值得进一步深入研究。