常见复合三角形问题的题型归类与求解策略
云南 唐明超 子银奎
解三角形是高中数学的核心知识点,重点研究三角形的三条边与三个角共六个基本元素,常规试题中一般是给出六个元素中的某几个具有关联的元素求解另外几个元素,主要考查正弦定理、余弦定理、三角形内角和定理、三角恒等变换等知识点的综合应用.解单个三角形的过程相对简单,但是解答有公共边的两个或三个三角形的复合问题就显得相对复杂,虽然本质还是解三角形,但问题的分析与解决过程对抽象概括能力、推理论证能力与运算求解能力的要求比较高,主要体现在正弦定理与余弦定理的有效选择以及多个知识点的综合运用.本文基于解三角形的基本原理和方法对一类具有公共边的复合三角形问题进行归类,并尝试对此类题型进行分析,给出一般性的求解策略,为学生开展学习、为教师开展教学研究活动提供参考素材.
类型1 解有一条公共边的两个三角形
1.1三角形内角平分线问题
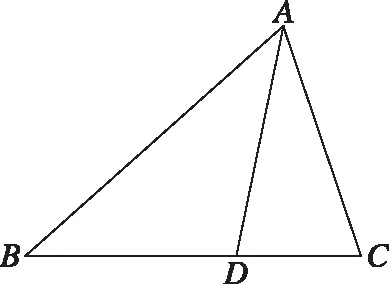
【例1】(2015·全国卷Ⅱ理·17)△ABC中,D是BC上的点,AD平分∠BAC,△ABD面积是△ADC面积的2倍.
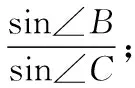
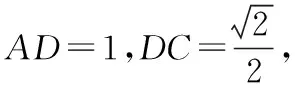
试题分析:从试题的呈现方式上看,试题由两个具有公共边的三角形复合得来,图形中含有三个不同的三角形,而且公共边恰好是大三角形的内角平分线;从知识的角度看,本题主要考查正弦定理、余弦定理等平面几何知识的综合运用.第(Ⅰ)问的求解需要根据已知条件中的面积关系并借助三角形的面积公式进行转化,选用三角形的不同面积公式可以得到不同的解法如下.



对于第(Ⅱ)问的解答需要充分用好已知条件及第(Ⅰ)问的结论,寻找相关量间的逻辑联系,建立已知量与未知量之间的等量关系,通过解方程得出答案,突出三角形中的方程思想.

1.2三角形的中线问题

试题分析:公共边是大三角形的中线,根据邻角或补角的性质可以考虑运用余弦定理建立方程组解题.

评析:该种方法具有一定的局限性,仅适用于确定了两个或确定更多基本量的三角形问题,对于其他类型的问题要尝试用好三角形的中线性质,灵活运用向量间的基本关系进行转化进而实现解题,如例3.
【例3】(2012·浙江卷理·15改编)在△ABC中,M是BC的中点,AM=1,∠BAC=60°,则△ABC面积的最大值=________.
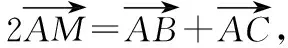


评析:对于公共边是中线的解三角形问题,首先要结合已知条件确定三角形的基本量,从已知基本量最多的三角形入手,利用余弦定理或是正弦定理构造关于边与角的方程组,通过解方程组实现三角形基本量的求解;但如果三角形中已知的基本量不足3个时要考虑借助中线的性质综合向量运算实现向量与数值之间的转化实现解题.
1.3三角形的高线问题
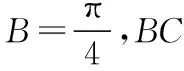


试题分析:当公共边为三角形的高线时,复合三角形中出现两个直角三角形,此时既可以考虑使用勾股定理也可以结合已知条件合理选用正弦定理和余弦定理解题,当然出现垂直这个特殊的几何特征,坐标法也是一种简单快捷的方法.


评析:在平面几何图形中求相关几何量时,需寻找各个三角形之间的内在逻辑联系,交叉使用公共条件,常常将所涉及的已知几何量与所要求的几何量集中到某一个三角形中,然后选用正弦定理与余弦定理求解.该题还可以使用坐标系法和向量运算实现解题,由于题目较基础,此处不予展开.
1.4其他三角形中连接顶点与对边任意一点的复合问题
【例5】(2019·浙江卷·14)在△ABC中,∠ABC=90°,AB=4,BC=3,点D在线段AC上,若∠BDC=45°,则BD=________,cos∠ABD=________.

试题分析:解决一般性的复合三角形问题,要基于已知条件寻找基本量之间的数量关系,尽可能地将三角形的边角关系确定下来,再借助正弦定理与余弦定理先计算已知基本量最多的三角形的边和角,多次运用正弦定理和余弦定理实现解题.

评析:利用正、余弦定理解决实际问题往往需要将实际问题抽象概括后尽可能地让已知量与未知量全部集中在一个三角形中,这样既可以使用正弦定理也可以使用余弦定理求解;实际问题经抽象概括后,已知量与未知量涉及两个或两个以上三角形,这时需作出这些三角形,先处理有两个条件及以上的三角形,再逐步解答其他的三角形,有时需要设出未知量,从几个三角形中列出方程(组),通过解方程(组)得出所要的解.
1.5三角形中连接三个顶点与内部任意一点的复合问题


(Ⅱ)若∠APB=150°,求tan∠PBA的值.

试题分析:该题可以理解为由三个两两共边的三角形复合而来,整体看上去相对复杂,但是认真读题后发现问题的本质还是解三角形,所以弄清楚三角形边与角的关系,将未知量固定于某个已知量较多的三角形中,逆向思考要解决该问题还需要什么条件,用什么定理,最后正向书写解答过程即可.


评析:解该题的关键在于列方程前把要知道的边用目标角表示出来,通过分析题目发现要解决第(Ⅰ)问首先要建立关于PA的方程,而建立方程先要确定一个包含PA边的三角形;第(Ⅱ)问的关键点还是要用目标角θ将未知边PB表示出来,再利用三角形内角和定理确定第三个角,这样在△PBA中就找到了四个可以建立关系的基本量,从而实现弦切互化得出结果;当然本题出现了垂直关系,还可以借助平面直角坐标系利用坐标运算实现解题.
类型2 三角形复合为四边形的问题
2.1四边形对角互补问题
【例7】(2014·全国卷Ⅱ文·17)四边形ABCD的内角A与C互补,AB=1,BC=3,CD=DA=2.
(Ⅰ)求C和BD;
(Ⅱ)求四边形ABCD的面积.
试题分析:该题中具有公共边的两个三角形复合为对角互补的四边形,而且四边形的边都是已知的,对于其中的任意一个三角形均能找出三个有关系的基本量;又由两个角互补可知余弦值互为相反数,所以可以考虑用两次余弦定理求出未知量;第(Ⅱ)问在第(Ⅰ)问的基础上很容易,分别求出两个三角形的面积,从而得出四边形的面积.


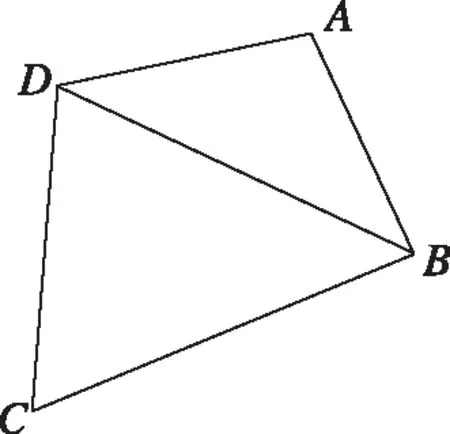
评析:整个解答过程完全基于三角形基本量的运算,虽然题目呈现的是四边形的边角关系,但是本质还是解三角形,用好对角互补这一条件,既可以根据余弦值互为相反数还可以根据正弦值相等建立等量关系实现解题.
2.2四边形的其他问题
【例8】(2018·全国卷Ⅰ理·17)在平面四边形ABCD中,∠ADC=90°,∠A=45°,AB=2,BD=5.
(Ⅰ)求cos∠ADB;
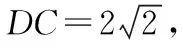
试题分析:该题中的两个三角形均有至少两个已知的基本量,可以很自然地想到利用余弦定理或是正弦定理求解,仔细观察发现△ABD中已知两边及其一边的对角,可以考虑将第(Ⅰ)问中未知量的求解置于△ABD中,进一步选择最简便的方法;第(Ⅱ)问在第(Ⅰ)问的基础之上可以利用两角互余确定cos∠BDC,从而求得BC.


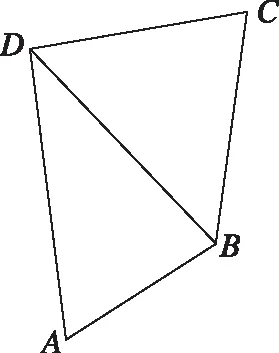
评析:解答该题的关键在于找出已知的基本量,将要求的基本量固定于一个具体的三角形中,合理选择正弦定理与余弦定理实现基本量的计算,另外注意利用互余的两个角正弦值与余弦值相等建立等量关系.


