非线性椭圆障碍问题很弱解的全局可积性
佟玉霞,杨雅琦,周艳霞
(华北理工大学理学院,河北 唐山063210)
1.引言
设Ω ⊂Rn(n ≥2)是一个有界正则区域,1 <p <n,这里正则域指的是具有有限测度并使得下文Hodge分解(引理2.1)成立的区域.例如,Lipschitz域和A型区域是正则的.
令ψ为Ω中任意取值于R ∪{-∞,+∞}的函数,θ ∈W1,r(Ω).令
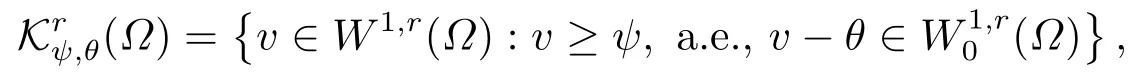
其中函数ψ为障碍函数,θ为边值函数.
本文考虑非线性椭圆方程


并且B(x,ξ)满足

现在介绍引理2.1中扰动向量场的Hodge分解|∇(v-u)|p-2∇(v-u)∈Lr/(r-p+1)(Ω):
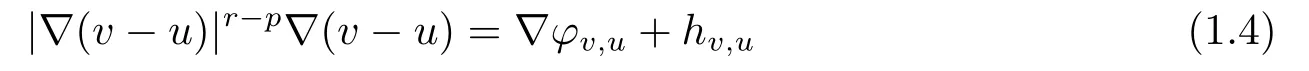
定义1.1称为(1.1)的-障碍问题的很弱解,max{1,p-1}<r <p,如果

上面定义中“很弱”的含义是指解u的可积指数r可以小于自然指数p,这不同于通常的经典弱解Ω)的假设.
首先回顾很弱解的相关进展.Iwaniec在文[1]中首次提出了很弱解的概念,对p-调和张量和弱拟正则映射,其弱导数的可积性低于自然指数.此外,Iwaniec-Sbordone[2]和Iwaniec等[3]分别考虑了变分积分的弱极小和r充分接近p时的弱p-调和型方程的正则性; 通过对扰动向量场的Hodge分解的方法,得到了变分积分的弱极小和弱p-调和方程的很弱解实际上是经典意义下的弱解.另一方面,与Iwaniec使用的方法不同的是,Lewis[4]通过调和分析技术获得了某些椭圆型方程很弱解的高阶可积性.后来,Lewis的调和分析技术又扩展到p-拉普拉斯算子[5-6]的抛物型方程组,以及各种非标准增长的椭圆和抛物型方程组[7-10].这从本质上说是使用了弱导数的逆Hlder不等式从而提高可积性来实现的[11].Greco等在文[12]中研究了非齐次p-调和方程
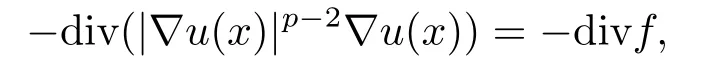
获得了算子H的估计.郑神州和方爱农[13]研究了非线性椭圆方程组

的很弱解,并且在扰动向量场的Hodge 分解的基础上,得到了其很弱解的微商具有自我提高的可积性.有关很弱解的更多结果,参见[1,4,12,14].
本文研究的可积性问题在非线性椭圆偏微分方程的正则性理论和相应的障碍问题中占有重要地位.在文[15]中,GAO等研究解决在某些合适的强制性条件和控制增长条件下,一类各项异性椭圆方程

令t >0,Ω ⊂Rn,弱Lt-空间或Marcinkiewicz空间[16]指的是包含所有满足
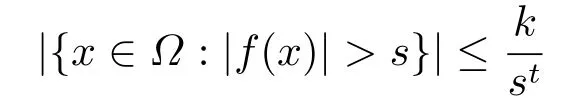
的可测函数f构成的空间,其中正常数k = k(f),s >0,|E|是E的n维测度.记为弱Lt-空间或(Ω).注意到,对于某些t >1,|Ω| <∞,如果f ∈(Ω),则对于任意的1 ≤τ <t,有f ∈Lτ(Ω).
本文主要结果如下.
定理1.1设θ*= max{θ,ψ},θ*∈W1,q(Ω),q >r.假设算子A(x,∇u)和B(x,∇u)满足结构性条件(1.2)和(1.3).那么存在一个常数ε0= ε0(n,p,Λ1,Λ2,λ) >0,使得对于(1.1)的(Ω)-障碍问题的任意很弱解u ∈θ+(Ω),max{1,p-1}<r <p <n,有

本文证明受高红亚和郑神州等人的论文[13,16,19-20]的启发,因为定义式(1.5)中很弱解不能做为容许函数,因此通过Hodge分解构造一个适当的容许函数.也就是说,本文的关键是通过Hodge分解选择一个合适的容许函数[2,13],然后根据Stampacchia引理[19]实现最终目标.需要说明的是,文[21]也考虑了一类A-调和方程的障碍问题的很弱解的全局可积性,但是其采用的方法主要是通过建立关于很弱解的梯度的弱逆Hlder不等式从而提高可积性来实现的.本文与其采用的方法是不同的.
2.预备知识
本节将介绍一些有用的引理.这些引理将在证明主要结论时起重要作用.用C(n,p,Λ1,···)表示仅依赖于规定数量的常数,各行中的常数C可能有不同.
首先,给出向量场的Hodge分解,见文[13]中的引理2.2.
引理2.1设v ∈(Ω,Rm),max{1,p-1}<r <p.则一定存在和散度自由的矩阵场h ∈(Ω,Rn×m),使得
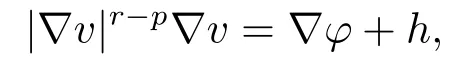
并且有估计式

其中C =C(n,p,Ω).
下面一个有效的工具就是著名的Stampacchia引理,参见文[22]中的引理4.1.
引理2.2令α,β为正常数,递减函数φ:[s0,+∞)→[0,+∞),满足
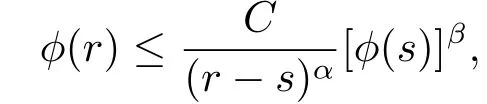
其中常数C >0,r >s ≥s0.于是
(i) 若β >1,则φ(s0+d)=0,这里
(ii) 若β =1,则当s ≥s0时,有
(iii) 若β <1,则当s ≥s0>0时,有

3.定理1.1的证明
证令θ*=max{θ,ψ}.对于任意的L >0,令

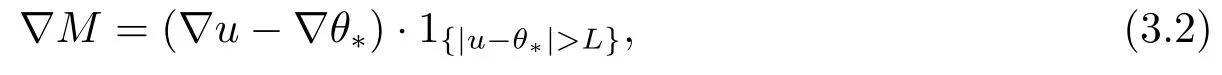
其中1{|u-θ*|>L}是集合E的特征函数,即当x ∈E时,1E=1.否则1E=0.
令

1) 显然v ∈W1,r(Ω);

因此(ψ-θ)+属于因此θ*∈θ+于是在∂Ω上θ*= max{θ,ψ} = θ = u,于是在∂Ω上M =0,从而v ∈θ+(Ω);
3) 第一种情况,当u-θ*<-L时,v = u-(u-θ*+L) = θ*-L >u ≥ψ; 第二种情况,有v =u ≥ψ; 第三种情况,v =u-(u-θ*-L)=θ*+L ≥θ*≥ψ.
因此,有

现在引入扰动向量场|∇(v-u)|p-2∇(v-u) ∈Lr/(r-p+1)(E)的Hodge分解,如引理2.1所示.于是,
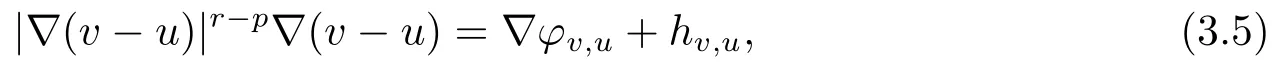
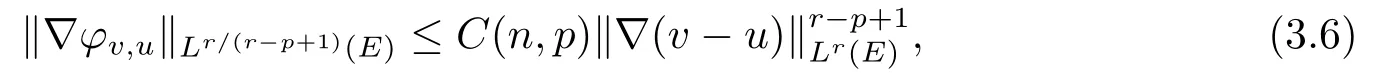
且
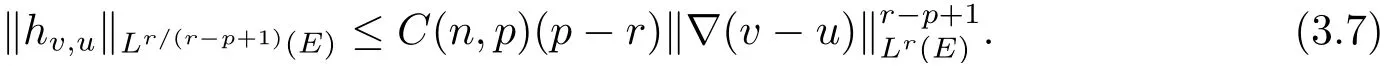

上式左侧利用(1.2),得到

这表明
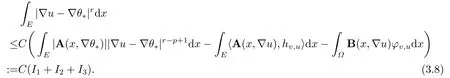
使 用(1.2),(1.3),(3.7),(3.6),Hlder不等式,Young不等式 和Sobolev-Poincar´e不等式,I1,I2,I3可估计如下:

这里ε >0足够小.


这里限制0 <p-r <ε0,其中ε0为待定常数.


并且

将J1和J2的估计值放在一起,得到
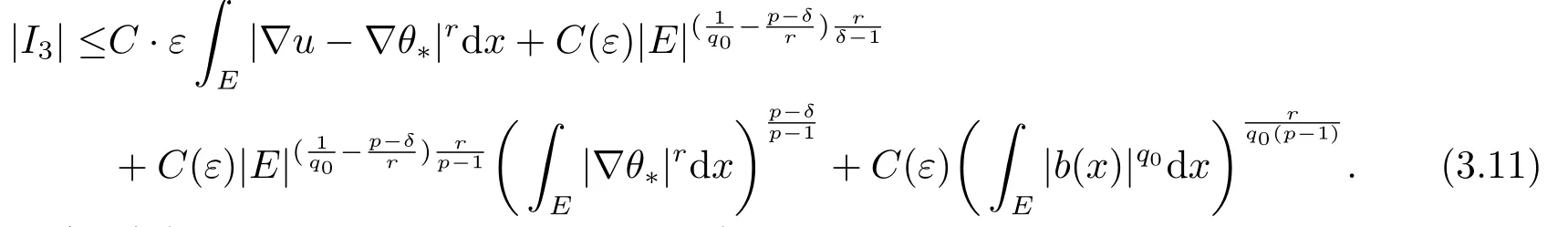
因此,结合(3.8),(3.9),(3.10)和(3.11),可得
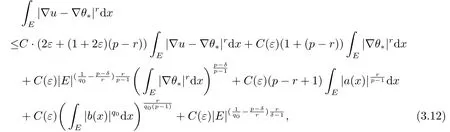
其中0 <p-r <ε0,取正常数ε,ε0足够小,使得于是(3.12)右边的第一项可以被左边吸收,于是得到

由于θ*∈W1,q(Ω),q >r,使用Hlder不等式可得
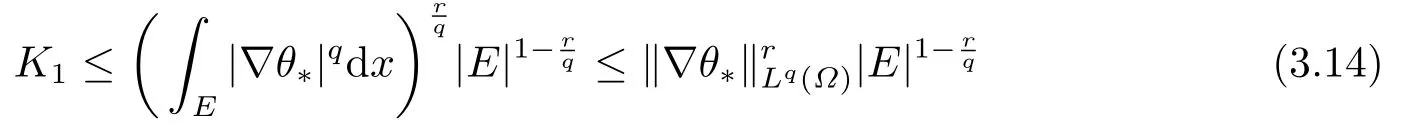
和


于是


和


于是有

将K1,K2,K3,K4和K5的估计值代入(3.13),得到
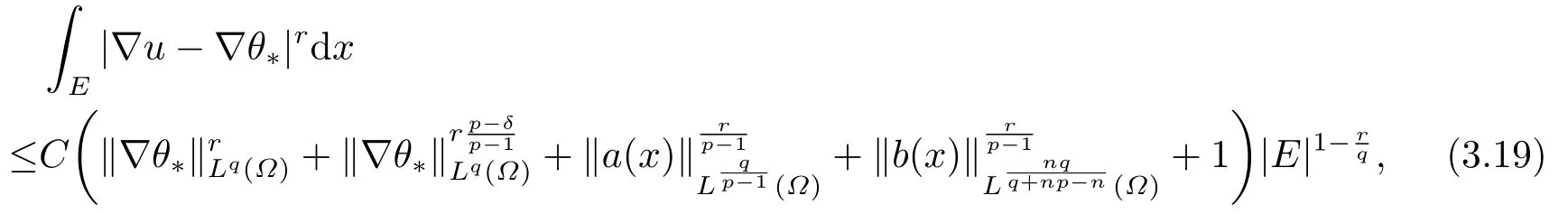
其中C =C(n,p,q,λ,Λ1,Λ2,δ,|Ω|).
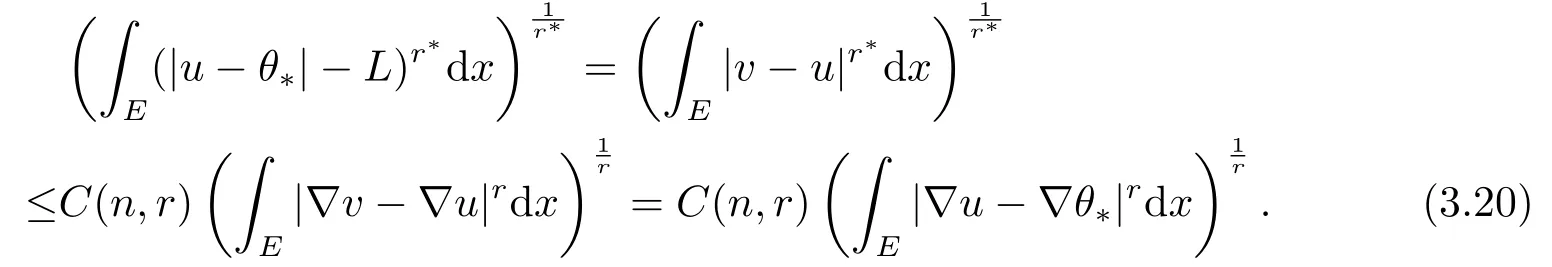

通过整理(3.19),(3.20),(3.21) 和E ={|u-θ*|>L},得到

其中C*=C*(n,p,q,λ,Λ1,Λ2,δ,|Ω|).于是有



情形(i) 如果1 ≤q <n,有β <1.在这种情况下,如果s ≥1,由引理2.2可以得到

其中
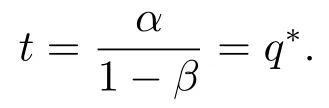
如果0 <s <1,有
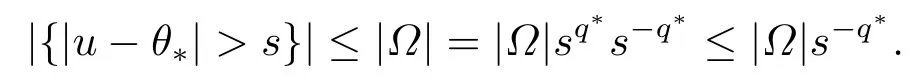
综上,得到

情形(ii) 如果q =n,有β =1.任意的1 ≤τ <∞,由(3.23)知
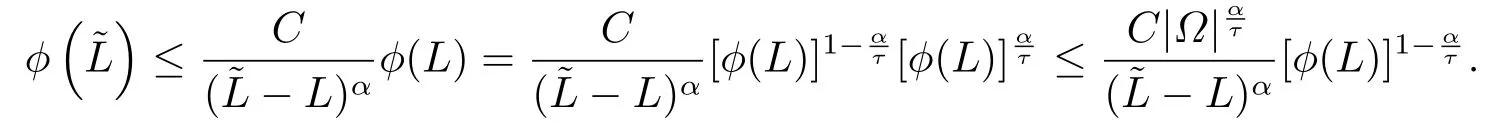
综上,根据Stampacchia引理得到u ∈θ*+Lτ(Ω).
情形(iii) 如果q >n,有β >1.引理2.2意味着对某些
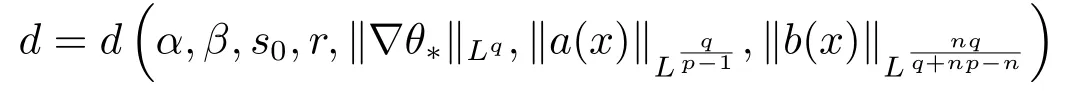
有φ(d)=0.因此|{|u-θ*|>d}|=0,这里u-θ*≤d在Ω中几乎处处成立.于是

证明完毕.
- 应用数学的其它文章
- New Iteration Method for a Quadratic Matrix Equation Associated with an M-Matrix
- 具有随机保费和交易费用的最优投资-再保险策略
- 带有N策略的不可靠重试队列的均衡策略分析
- A Smoothing Newton Algorithm for Tensor Complementarity Problem Based on the Modulus-Based Reformulation
- The Center Problems and Time-Reversibility with Respect to a Linear Involution
- Boundary Value and Initial Value Problems with Impulsive Terms for Nonlinear Conformable Fractional Differential Equations

