高考数学开放性问题的类型及求解探索

童其林

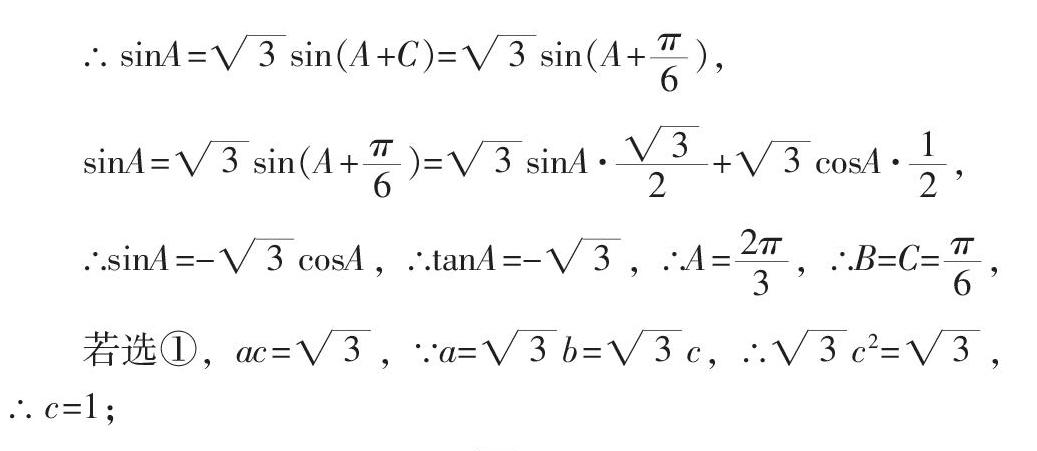
高考评价体系由“一核四层四翼”组成，其中，“一核”是高考的核心功能，即“立德树人、服务选才、引导教学”，回答“为什么考”的问题;“四层”为高考的考查内容，即“核心价值、学科素养、关键能力、必备知识”，回答“考什么”的问题;“四翼”为高考的考查要求，即“基础性、综合性、应用性、创新性”，回答“怎么考”的问题. 那么，在“四翼”考查要求下，有哪些命题原则？在“四翼”考查要求下，新高考有哪些新题型？

一般来说，在“四翼”考查要求下，新高考数学有以下三个命题原则：一是注重学科间的渗透和交叉，适当增加具有自然科学和社会人文学科情境的试题，促进学科间的融合以及对核心素养的有效考查;二是关注探究能力、数学学习能力的考查，设计结论开放、解题方法多样、答案不唯一、结构不良的试题，增强试题的开放性和探究性，对学生的创新能力进行考查;三是通过调整试卷结构，打破固有模式，探索试题排列新方式，努力破除复习备考中题海战术和套路训练的影响.

在“四翼”考查要求下，新高考数学将有以下五种新题型：一是多选题，选择题答案不唯一，存在多个正确选项;二是逻辑思维题，以日常生活情境考查推理、论证、比较、评价等逻辑思维能力;三是数据分析题，给出一些材料背景，以及相关数据，要求考生读懂材料，获取信息，根据材料给出的情境、原理以及猜测等，自主分析数据，得出结论，并解决问题;四是举例题，要求考生通过给出的已知结论、性质和定理等条件，从题干中获取信息，整理信息，写出符合题干的结论或具体实例;五是开放题，问答题开放设问，答案并不唯一，要求考生能綜合运用所学知识，进行探究，分析问题并最终解决问题.

本文主要谈谈开放性问题的类型及求解. 所谓开放型问题是相对有明确条件和明确结论的封闭式问题而言的，是指题目的条件不完备或结论不确定的问题.

一、条件开放型

这类题目的特点是给出了题目的结论，但没有给出满足结论的条件，并且这类条件常常是不唯一的，需要解题者从结论出发，通过逆向思维去判断能够追溯出产生结论的条件，并通过推理予以确认.这种条件探究性问题实质上是寻找使命题为真的充分条件（未必是充要条件）.解决此类问题的策略有两种，一种是将结论作为已知条件，逐步探索，找出结论成立所需的条件，这也是我们通常所说的“分析法”;第二种是假设题目中指定的探索条件，把它作为已知，并结合其他题设进行推导，如果能正确推导出结论，则此探索条件就可以作为题设条件，直觉联想、较好的洞察力都将有助于这一类问题的解答.

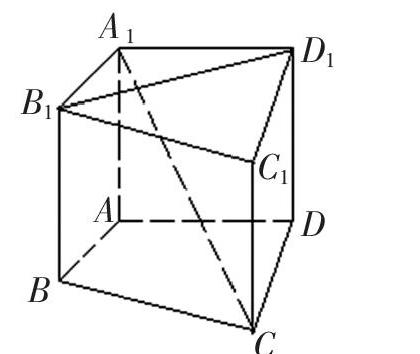
例1. 如图，在直四棱柱A1B1C1D1—ABCD中，当底面四边形ABCD满足条件__________时，有A1C⊥B1D1（注：填上你认为正确的条件即可，不必考虑所有可能的情况）

解析：本题是条件探索型试题，即寻找结论A1C⊥B1D1成立的充分条件，由AA1⊥平面A1C1以及A1C⊥B1D1（平面A1C1的一条斜线A1C与面内的一条直线B1D1互相垂直），容易联想到三垂线定理及其逆定理. 因此，欲使A1C⊥B1D1，只需B1D1与CA1在平面A1C1上的射影垂直即可. 显然，CA1在平面A1C1上的射影为A1C1，故当B1D1⊥A1C1时，有A1C⊥B1D1，又由于直四棱柱的上、下底面互相平行，从而B1D1∥BD，A1C1∥AC. 因此，当BD⊥AC时，有A1C⊥B1D1. 由于本题是要探求使A1C⊥B1D1成立的充分条件，故当四边形ABCD为菱形或正方形时，依然有BD⊥AC，从而有A1C⊥B1D1，故可以填：①AC⊥BD或②四边形ABCD为菱形，或③四边形ABCD为正方形中的任一个条件即可.

点评：AC⊥BD是结论A1C⊥B1D1成立的充要条件，而所填的ABCD是正方形或菱形则是使结论A1C⊥B1D1成立的充分而不必要的条件.本例中，满足题意的充分条件不唯一，具有开放性特点，这类试题重在考查基础知识的灵活运用以及归纳探索能力.

例2. 有一道题目由于纸张破损，有一条件看不清楚，具体如下：

在△ABC中，已知a=■，____________，2cos2（■）=（■-1）cosB，求角A.

经推断，破损处的条件为三角形一边的长度，该题的答案A=60°是唯一确定的，试将条件补充完整，即空白处应填的条件是__________.

解析：2cos2（■）=（■-1）cosB？圳2·■=（■-1）cosB？圳cosB=■.

又B∈（0°， 180°），所以B=45°.

（1）■=■？圯b=■，

检验：■=■？圳■=■？圳sinA=■，又A∈（0°， 180°），且a>b，所以A=60°或者A=120°，这与已知角A的解为唯一解矛盾.

（2）B=45°，又A=60°，所以C=75°，

■=■？c=■.

检验：■=■？圳■=■？圳sinA=■. 又A∈（0°，180°），且c>a，所以A=60°.

故应填的条件是：c=■.

点评：本题所求的边要么是b，要么是c，但还要满足三角形存在这个条件，所以检验是必要的，否则容易忽视隐含条件而引起错误.

例3. 在①ac=■，②csinA=3，③c=■b这三个条件中任选一个，补充在下面问题中，若问题中的三角形存在，求c的值;若问题中的三角形不存在，说明理由.

问题：是否存在△ABC，它的内角A， B， C的对边分别为a， b， c，且sinA=■sinB，C=■，________？

注：如果选择多个条件分别解答，按第一个解答计分.

解析：在△ABC中，它的内角A， B， C的对边分别为a， b， c，且sinA=■sinB，C=■，这是公共条件. 在此条件下，从①ac=■，②csinA=3，③c=■b这三个条件中任选一个，求问题中的三角形是否存在，若存在，求c的值，若不存在，说明理由.

公共条件怎样用？通常有两种转化方法，一是在sinA=■sinB中，利用正弦定理角化边，得到a，b的比例关系，再设出长度长度，由余弦定理得到c的长度，根据选择的条件进行分析判断和求解;二是利用诱导公式和两角和的三角函数公式求得tanA的值，得到角A， B， C的值，然后根据选择的条件进行分析判断和求解. 具体解法有如下几种：

解法一：由sinA=■sinB可得：■=■，不妨设a=■m，b=m（m>0），

则c2=a2+b2-2abcosC=3m2+m2-2×■m×m×■=m2，即c=m.

选择条件①的解法：

据此可得：ac=■m×m=■m2=■，∴ m=1，此时c=m=1.

选择条件②的解法：

据此可得：cosA=■=■=-■，

则sinA=■=■，此时：csinA=m×■=3，则：c=m=2■.

选择条件③的解法：

可得■=■=1，c=b，

与条件c=■b矛盾，则问题中的三角形不存在.

解法二：∵ sinA=■sinB，C=■，B=？仔-（A+C），

∴ sinA=■sin（A+C）=■sin（A+■），

sinA=■sin（A+■）=■sinA·■+■cosA·■，

∴sinA=-■cosA，∴tanA=-■，∴A=■，∴B=C=■，

若选①，ac=■，∵a=■b=■c，∴■c2=■，∴ c=1;

若选②，csinA=3，则■=3，c=2■;

若选③，与条件c=■b矛盾.

点评：在处理三角形中的边角关系时，一般全部化为角的关系，或全部化为边的关系.题中若出现边的一次式一般采用到正弦定理，出现边的二次式一般采用到余弦定理.应用正、余弦定理时，注意公式变式的应用.解决三角形问题时，注意角的限制范围.

值得注意的是，本例属于结构不良问题.结构不良的问题并不是指问题本身有什么错误或者不恰当，而是指它没有明确的结构或者解决途径. 例如，修电脑，其初始状态不明确，要先检查电脑故障状态在哪？再如，让学生考察当地城市环境污染状况，写一篇论文，其初始状态、目标状态、甚至问题的解决方案都不明确，是名副其实的结构不良问题. 近年来，结构不良问题引起了研究者的关注，因为现实生活中充斥着大量结构不良问题需要解决者从诸多现象中自己分析、设计出解决方案. 数学“结构不良”问题比开放性问题的范畴更大、更广.

二、结论开放型

这类题目的特点是给出一定的条件，要求从条件出发去探索结论，而结论往往是不唯一的，甚至是不确定的，或给出特例后通过归纳得出一般性结论. 解决此类问题的策略有：从已知条件出发，运用所学过的知识进行推理、探究或实验得出结论;通过归纳得出一般性结论，再去证明;对多种结论进行优化（内含分类讨论）等.

例4 老师给出一个函数y=f（x），四个学生甲、乙、丙、丁各指出这个函数的一个性质：

甲：对于x∈R，都有f（1+x）=f（1-x）;

乙：在（-∞， 0] 上函数递减;

丙：在（0， +∞）上函数递增;

丁：f（0）不是函数的最小值.

如果其中恰有三个人说得正确，请写出一个这样的函数：____________.

解析：首先看甲的话，所谓“对于x∈R，都有f（1+x）=f（1-x）”，其含义即为：函数f（x）的图像关于直线x=1对称.数形结合，不难发现：甲与丙的话相矛盾.（在对称轴的两侧，函数的单调性相反）

因此，我们只需选择满足甲、乙、丁（或乙、丙、丁）条件的函数即可.

如果我们希望找到满足甲、乙、丁条件的函数，则需要认识到：所谓函数在（-∞，0]上单调递减，并不是说函数f（x）的单调递减区间只有（-∞，0].考虑到关于直线x=1的对称性，我们不妨构造函数，使之在（-∞，1] 上单调递减，这样，既不与乙的话矛盾，也满足丁所说的性质.如f（x）=（x-1）2即可.

实际上，f（x）=（x-1）2+m（m∈R）都满足题设，有无数个.

如果希望找到满足乙、丙、丁条件的函数，则分段函数是必然的选择.如f（x）=-x+1， x≤0x， x>0.

实际上，f（x）=-x+k（k>0）， x≤0x， x>0也满足题设，有无数个.

点评：本题考查考生对于函数性质的理解和掌握.思考这样的问题，常常需要从熟悉的函数（一次、二次、反比例函数，指数、对数、三角函数等）入手，另外，分段函数往往是解决问题的关键.另外，本题也是举例题，属于开放性问题的范畴.

例5. 函数f（x）的定义域为R，且f（x+1）与f（x+2）都为奇函数，则（）

A. f（x）为奇函数B. f（x）为周期函数

C. f（x+3）为奇函数 D. f（x+4）为偶函数

解析：因为g（x）= f（x+1）是奇函数，所以g（-x）+g（x）=0，即f（-x+1）+ f（x+1）=0，所以f（x）关于（1，0）对称，同理 f（-x+2）+ f（x+2）=0，f（x）關于点（2， 0）对称.

因此，f（2-x）+ f（x）=0，f（（4-x）+ f（x）=0，所以f（2-x）=f（4-x），所以f（x）= f（2+x），所以f（x）是以2为周期的函数. 所以f（x），f（x+3）f（x+4），均为奇函数. ABC正确，所以选ABC.

点评：在新高考中（比如2020年高考的山东卷、海南卷），这样的多选题一般有四道，通常设置在第9题至12题之间. 对于本题而言理解和记住函数对称性和周期性的三个结论是很重要的：

定理1. 函数 y= f（x）的图像关于点A（a， b）对称的充要条件是f（x）+ f（2a-x）=2b.

推论1：函数 y= f（x）的图像关于原点O对称的充要条件是f（x）+ f（-x）=0.

推论2：函数 y= f（x）的图像关于点A（a， b）对称的充要条件是f（a+x）+ f（a-x）=2b.

定理2. 函數 y= f（x）的图像关于直线x=a对称的充要条件是f（a+x）= f（a-x），即f（x）= f（2a-x）.

推论：函数 y= f（x）的图像关于y轴对称的充要条件是

f（x）= f（-x）.

定理3. ①若函数y= f（x）图像同时关于点A（a， c）和点B（b，c）成中心对称（a≠b），则y= f（x）是周期函数，且2|a-b| 是其一个周期.

②若函数y= f（x）图像同时关于直线x=a和直线x=b成轴对称（a≠b），则y= f（x）是周期函数，且2|a-b| 是其一个周期.

③若函数y= f（x）图像既关于点A（a， c）成中心对称又关于直线x=b成轴对称（a≠b），则y= f（x）是周期函数，且4|a-b|是其一个周期.

（以上结论的证明留给读者）

例6. 已知a>0，b>0，且a+b=1，则（）

A. a2+b2≥■B. 2a-b>■

C. log2a+log2b≥-2D. ■+■≤■

解析：对于A，a2+b2=a2+（1-a）2=2a2-2a+1=2（a-■）2+■≥■，

当且仅当a=b=■时，等号成立，故A正确;

对于B，a-b=2a-1>-1，所以2a-b>2-1=■，故B正确;

对于C， log2a+log2b=log2ab≤log2（■）2=log2■=-2，

当且仅当a=b=■时，等号成立，故C不正确;

对于D，因为（■+■）2=1+2■≤1+a+b=2，

所以■+■≤■，当且仅当a=b=■时，等号成立，故D正确，故选：ABD.

点评：本题主要考查不等式的性质，综合了基本不等式，指数函数及对数函数的单调性，侧重考查数学运算的核心素养.

三、条件和结论都开放型

有些题目条件和结论都是不确定的，但是给出了一定量的信息和情景，要求解题者在题目给出的情景中，自行设定条件，自己寻找结论，自己构建命题并进行演绎推理.

例7. ？琢、？茁是两个不同的平面，m、n是平面？琢及？茁之外的两条不同直线. 给出四个论断：①m⊥n;②？琢⊥？茁;③n⊥？茁;④m⊥？琢. 以其中三个论断作为条件，余下一个论断作为结论，写出你认为正确的一个命题：______________.

解析：本题通过改变条件与结论之间呈现的顺序与组合，使问题具备了探索性，将分析—猜想—证明的思维过程巧妙地融入了解题过程;同时也使问题具有了开放性，走出了数学答案唯一确定的误区. 它们以新颖的知识呈现方式改变考生的常规思维，考查考生的创新能力.

答案是：②③④？圯①或①③④？圯②.

例8. 三角形ABC的三个内角A， B， C的对边的长分别为a， b， c，有下列两个条件：（Ⅰ）a， b， c成等差数列;（Ⅱ）a， b， c成等比数列.

现给出三个结论：

①0

请你选取给定的两个条件中的一个条件为条件，三个结论中的两个为结论，组建一个你认为正确的命题，并证明之.

解析：可以组建如下正确的命题：

命题一：△ABC中，若a、b、c成等差数列，求证：（Ⅰ）0

命题二：△ABC中，若a、b、c成等差数列，求证：（Ⅰ）0

命题三：△ABC中，若a、b、c成等差数列，求证：（Ⅰ）acosC+ccosA=■;（Ⅱ）1<■≤■.

命题四：△ABC中，若a、b、c成等比数列，求证：（Ⅰ）0

下面给予证明：

命题一：（Ⅰ）因为a、b、c成等差数列，所以2b=a+c，故b=■.

cosB=■=■=■≥■=■.

又B∈（0， ？仔），所以0

（Ⅱ）acosC+ccosA=a×■+c×■=b=■.

命题二：（Ⅰ）同命题一（Ⅰ）.

（Ⅱ）■=■=cosB+sinB=■cos（B-■）.

因为0

cos（B-■）≤1，所以1<■cos（B-■）≤■.

命题三：可证明0

命题四：（Ⅰ）因为a、b、c成等比数列，所以b2=ac，cosB=■=■≥■=■，且B∈（0， ？仔），所以0

（Ⅱ）同命题二（Ⅱ）.

点评：在考场上，只要四个命题中选择一种，并证明即可，但在平时的学习过程中，应该尝试各种可能的情形进行分析求解.

练习题

1. 设同时抛掷两个质地均匀的四面分别标有1，2，3，4的正四面体一次. 记事件A={第一个四面体向下的一面出现偶数};事件B={第二个四面体向下的一面出现奇数};C={两个四面体向下的一面或者同时出现奇数或者同时出现偶数}. 给出下列说法：

① P（A）=P（B）=P（C）;② P（AB）=P（AC）=P（BC）;

③ P（ABC）=■;④ P（A）P（B）P（C）=■，

其中正确的有（ ）

A. 0个B. 1个C. 2个D. 3個

2. 已知函数f（x）=lnx-x+■，给出下列四个结论，则所有正确结论是（ ）

A. 曲线y=f（x）在x=1处的切线方程为x+y-1=0

B. f（x）恰有2个零点

C. f（x）既有最大值，又有最小值

D. 若x1x2>0且f（x1）+ f（x2）=0，则x1x2=1

3. 能说明“若f（x）>f（0）对任意的x∈（0，2]都成立，则f（x）在 [0， 2] 上是增函数“为假命题的一个函数是_________.

4. 已知l，m是平面？琢外的两条不同直线.给出下列三个论断：① l⊥m;② m∥？琢;③ l⊥？琢.

以其中的两个论断作为条件，余下的一个论断作为结论，写出一个正确的命题：__________.

5. 已知△ABC的内角 A， B， C 的对应边分别为 a， b， c，

在①■cosC（acosB+bcosA）=csinC;

② asin■=csinA;

③（sinB-sinA）2=sin2C-sinBsinA，

这三个条件中任选一个，补充在下面问题中，当____________时，求sinA·sinB的最大值.

练习题参考答案

1. D. 2. ABD. 3. y=sinx，或者f（x）=0，x=04-x，x∈（0， 2]（答案不唯一）

4. 如果l⊥α，m∥α，则l⊥m.

5. 解析：若选①，则由正弦定理■cosC（sinAcosB+sinBcosA）=sinCsinC，■cosCsin（A+B）=sinCsinC，■=tanC，C=■.

若选②，则由正弦定理知：

sinAsin■=sinCsinA，cos■=sinC=2sin■cos■

sin■=■，C=■.

若选③，则有正弦定理知（b-a）2=c2-bc，

∴ b2+a2-c2=bc，由余弦定理知：cosC=■，C=■，

A+B=■，∴ sinA·sinB=sinA·sin（■-A）=sinA·（■cosA+■sinA）=■sinA·cosA+■sin2A=■sin2A+■（1-cos2A）=■sin（2A-■）+■.

∵ A∈（0，■），∴ 2A-■∈（-■，■）.

所以当A=■时，sinA·sinB的最大值是■.

责任编辑 徐国坚