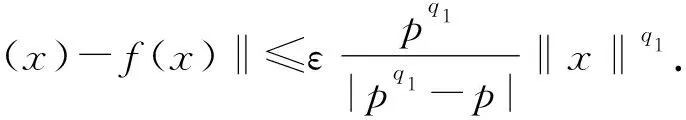Banach 3-Lie代数上两类映射的稳定性

秦宇帆，林 洁，姜敬敬

(1.中国民航大学理学院，天津 300300；2.中国民航大学中欧航空工程师学院，天津 300300)

0 引言

1985年，Filippov[1]引进了n-Lie代数(或Filippov代数)的概念.n元Lie积是n-线性、反对称的，且满足广义的Jacobi恒等式.当n=3时，3元Lie积是Nambu括号的特殊情形，Nambu括号是由Nambu[2]在1973年引进的，并且在物理上广为人知.3-Lie代数被应用于多重M2-膜的相关研究中，且其与数学、数学物理的许多重要领域有紧密联系[3-4].因此，许多研究者对3-Lie代数感兴趣.[5-12]

函数方程的稳定性在1940年首次被Ulam[6]提出，他提出下列问题：在什么情况下存在一个可加映射逼近一个近似可加映射？设A和B是两个Banach空间，Hyers证明了若ε>0，f：A→B满足

‖f(x+y)-f(x)-f(y)‖≤ε，∀x，y∈A，

则存在唯一的可加映射T：A→B使得

‖f(x)-T(x)‖≤ε，∀x，y∈A.

近年来，不断有这方面的成果涌现出来.文献[7]给出了n阶阿贝尔群G中函数方程

的广义稳定性结论和应用(p是一固定的正整数)[7]；文献[8]建立了关于函数方程

的3-Lie乘子的稳定性和超稳定性.

本文中，记C是复数域，N是自然数集.

1 预备知识

定义1.1[1]设A是一个向量空间，[-，-，-]：A×A×A→A是A上的一个3-线性反对称运算.若∀x，y，a，b，c∈A有[x，y[a，b，c]]=[[x，y，a]，b，c]+[a，[x，y，b]，c]+[a，b，[x，y，c]]，则称(A，[-，-，-])为一个3-Lie代数.

定义1.2设A是一个3-Lie代数.若在A上存在一个范数‖·‖使得

‖[x，y，z]‖≤‖x‖‖y‖‖z‖，∀x，y，z∈A，

则称A为一个赋范3-Lie代数.若(A，‖·‖)是一个Banach空间，则称赋范3-Lie代数A为一个Banach 3-Lie代数.

定义1.3[9]设A是一个3-Lie代数，H，D，ɡ：A→A为线性映射.如果∀x，y，z∈A，有H([x，y，z])=[H(x)，H(y)，H(z)]，则称H是A上的一个同态；若∀x，y，z∈A，有D([x，y，z])=[D(x)，y，z]+[x，D(y)，z]+[x，y，D(z)]，则称D是A上的一个导子；若存在线性映射ɡ1，ɡ2，ɡ3：A→A，使得

[ɡ(x)，y，z]+[x，ɡ1(y)，z]+[x，y，ɡ2(z)]=ɡ3([x，y，z])，∀x，y，z∈A，

则称ɡ是A上的一个广义导子.

2 Banach 3-Lie代数上同态的稳定性

引理2.1[10]设V和W是两个C-向量空间.f：V→W是一个可加映射，满足f(μx)=μf(x)，∀x∈V，μ∈T1∶={λ∈C||λ|=1}，则f是C-线性的.

引理2.2设p是一个正整数，f：A→A是一个映射，满足

(1)

则f是C-线性的.

证明在(1)式中，取x=y=z=0，μ=1，则f(0)=0.再令(1)式中x=y=0，得pf(μz)=pμf(z)，∀z∈A，μ∈T1.故f(μz)=μf(z)，∀z∈A，μ∈T1.

下证f是可加的.用pz代替(1)式中的x，y，且令μ=-1，有

pf(z)=f(pz)，∀z∈A.

进而有

pf(x+y)=f(px+py)，∀x，y∈A.

再用px，py分别代替(1)式中的x和y，且取z=0，得

pf(x+y)=f(px+py)，∀x，y∈A.

显然有

f(px+py)=f(px)+f(py)，∀x，y∈A.

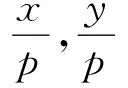
定理2.1设A是C上的一个Banach 3-Lie代数，φ，ψ1：A×A×A→[0，+∞)是映射且满足：

(2)

(3)

(4)

∀x，y，z∈A.假设f：A→A是一个映射使得f(0)=0，且：

(5)

‖f([x，y，z])-[f(x)，f(y)，f(z)]‖≤ψ1(x，y，z)，

(6)

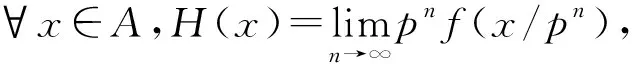
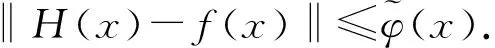
(7)

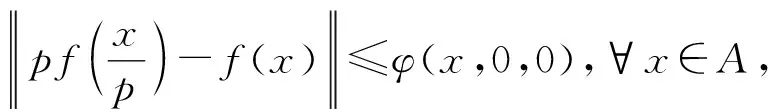
(8)

∀x∈A，n∈N.用x/pm代替(8)式中的x，且不等式两边同乘pm得

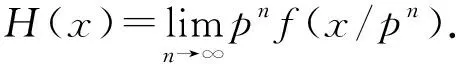
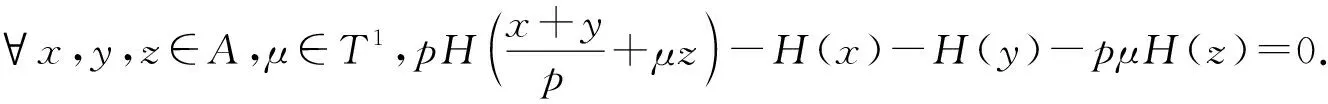
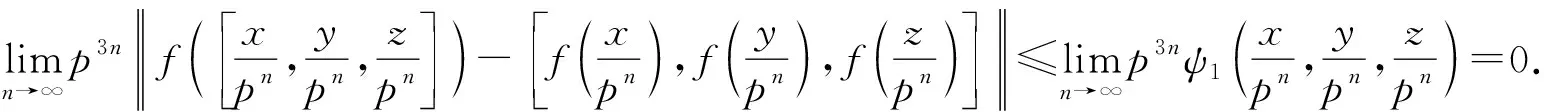
∀x，y，z∈A.故H是一个同态.

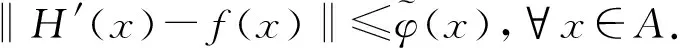
则

所以H′(x)=H(x)，∀x∈A.

推论2.1设A是一个Banach 3-Lie代数，ε，p1，p2，p3，p4，p5，p6，p7，p8，q1，q2，q3是实数且满足ε>0，p1，p2，p4，p6>1(或p1，p2，p4，p6<1)，q1，q2，q3>1(或q1，q2，q3<1)，f：A→A是一个映射使得f(0)=0且对∀x，y，z∈A，

‖f([x，y，z])-[f(x)，f(y)，f(z)]‖≤
ε(‖x‖p1+‖x‖p2‖y‖p3+‖x‖p4‖z‖p5+‖x‖p6‖y‖p7‖z‖p8).

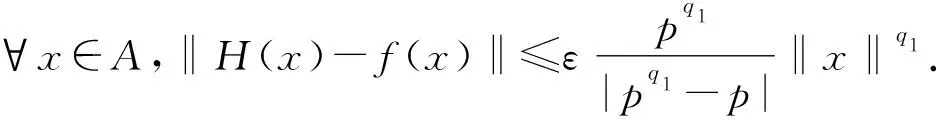
3 Banach 3-Lie代数上的导子的稳定性

定理3.1设A是C上的Banach 3-Lie代数，φ，ψ1：A×A×A→[0，+∞)是映射且满足：

∀x，y，z∈A.假设f：A→A是一个映射使得f(0)=0，且对∀x，y，z∈A，μ∈T1，以下不等式成立：

‖f([x，y，z])-[f(x)，y，z]-[x，f(y)，z]-[x，y，f(z)]‖≤ψ1(x，y，z)，

则存在唯一导子D：A→A使得

证明类似于定理2.1的证明，此处略去.

推论3.1在与推论2.1相同的条件下，f：A→A是一个映射，满足f(0)=0，且

‖f([x，y，z])-[f(x)，y，z]-[x，f(y)，z]-[x，y，f(z)]‖≤
ε(‖x‖p1+‖x‖p2‖y‖p3+‖x‖p4‖z‖p5+‖x‖p6‖y‖p7‖z‖p8)，

∀x，y，z∈A.则存在唯一导子D：A→A满足

4 Banach 3-Lie代数上的广义导子的稳定性

定理4.1设A是C上的一个Banach 3-Lie代数，φ，ψ1：A×A×A→[0，+∞)是映射，满足：

∀x，y，z∈A.假设f，f1，f2，f3：A→A是映射使得f(0)=0，f1(0)=0，f2(0)=0，f3(0)=0，且：

‖[f(x)，y，z]+[x，f1(y)，z]+[x，y，f2(z)]-f3([x，y，z])‖≤ψ1(x，y，z)，

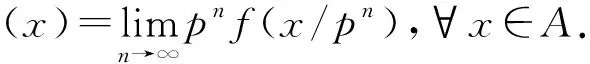
证明类似于定理2.1的证明，此处略去.

推论4.1在与推论2.1相同的条件下，f，f1，f2，f3：A→A是映射，f(0)=0，f1(0)=0，f2(0)=0，f3(0)=0，且满足：

‖[f(x)，y，z]+[x，f1(y)，z]+[x，y，f2(z)]-f3([x，y，z])‖≤
ε(‖x‖p1+‖x‖p2‖y‖p3+‖x‖p4‖z‖p5+‖x‖p6‖y‖p7‖z‖p8)，