基于低秩矩阵填充的推荐算法

潘 伟，胡春安

(江西理工大学信息工程学院，赣州 341000)

在许多实际问题中，如信号处理[1-2]、多标签分类[3-4]、推荐系统[5]等问题，数据是以矩阵的形式呈现的，由于各种原因，对于某个矩阵，无法得到整个矩阵的元素值，有很大一部分元素是缺失的，如何将这些缺失的值准确合理地填充，是矩阵填充要解决的问题。

在推荐系统中，评分矩阵的行和列通常是相互关联的，而低秩矩阵假设可以很好地反映出行与列之间的相关性。然而，矩阵的秩函数是非凸的、不连续的，即最小化矩阵的秩是一个不确定能不能在多项式时间内解决(NP-hard)的问题，为了解决这个问题，通常的方法是将矩阵Y∈Rm×n分解成两个低秩矩阵U和V，其中U∈Rm×r，V∈Rn×r，秩r远小于m和n，使得UVT和原矩阵Y在已知元素位置处尽量相等。通常使用梯度下降和交替最小化方法来优化求解[6-7]。由于目标函数在U和V中不是联合凸的，这种方法的收敛速度很慢。

另一种方法是用矩阵的奇异值的和，即矩阵的核范数，来替代矩阵的秩进行求解。Candès等[8]提出矩阵的核范数是矩阵秩的包络，使用凸优化模型来解决此问题，将最小化矩阵的秩问题转化为核范数最小化模型来进行求解。针对该模型，有很多优化算法被提出。半定规划(semi-definite programming)[8]是早期提出来的一个方法，然而该方法的时间复杂度和空间复杂度较高且只适用于矩阵维数很小的情况下。为此，文献[9]提出了一种适用于较大规模的矩阵填充的奇异值阈值算法(singular value thresholding，SVT)，该算法在交替迭代的过程中保持了矩阵填充时的低秩性，然而该算法涉及奇异值分解，计算量会随着矩阵规模变大而增加。文献[10]提出了APG(accelerated proximal gradient)算法，其收敛速度相比于SVT更有竞争力。另外，压缩感知[11]领域的贝叶斯学习方法[12-13]也可以应用到矩阵填充问题上。在贝叶斯框架下，低秩矩阵填充问题的拟合误差和低秩性可以自动地平衡。贝叶斯学习方法虽然可以提高重构性能，但是它在学习过程中有着烦琐的矩阵求逆运算。广义近似消息传递(generalized approximate message passing，GAMP)[14]是近年来提出的消息传递框架下的贝叶斯迭代算法，其优点是在迭代计算时不需要计算逆矩阵，在迭代过程中，各数值的计算与先验分布参数的取值有关。

现针对推荐系统中的评分矩阵稀疏性问题，用矩阵填充来进行建模，提出一种新的矩阵填充方法，首先采用分层高斯先验模型[15]促进矩阵的低秩性，然后通过GAMP迭代得到评分矩阵后验分布的近似估计，规避贝叶斯学习算法中矩阵求逆的过程，同时加入阻尼步骤以促进算法收敛，得到填充后的评分矩阵，最后在真实数据集上进行实验评估，以期在预测用户实际评分时得到更好的预测精度。

1 低秩矩阵填充理论

矩阵填充技术是近年来提出的一类数据降维模型，主要研究了对于一个未知的矩阵，如何通过已知的部分矩阵元素来合理地将缺失的数据进行填充。如果不加其他的约束，仅由部分少量的矩阵元素来恢复出整个矩阵，则满足要求的矩阵有无数多个，因此矩阵填充是一个非适定性问题。然而，若原始矩阵Y∈RM×N是一个受约束的低秩矩阵，则可以通过优化方法，将原始矩阵Y分解成低秩矩阵X与稀疏的噪声矩阵E之和，从而使得矩阵X与原矩阵Y之间的差异最小化。从数学上讲，对矩阵Y进行恢复的优化问题可表述为

(1)

由于式(1)所示的优化问题是NP(nondeterminism polynomial)难问题，文献[8]利用矩阵的秩与其非零奇异值的个数相等这个性质将此优化问题的秩函数进行凸松弛，即用矩阵的核范数替代矩阵的秩，因此问题可转化为

(2)

2 基于低秩矩阵填充的推荐算法

2.1 分层高斯先验

为了促进矩阵X的低秩性，采用了一种分层高斯先验模型[15]。在模型的第一层，假设矩阵X的列xn相互独立且服从均值为零、方差为Σ-1的高斯分布，公式为

(3)

式(3)中：Σ∈RM×M为精度矩阵。在模型的第二层，采用了Wishart分布作为超先验来描述第一层概率模型的超参数Σ,表示为

(4)

式(4)中：∝为等价于某一乘法常数；det(·)为矩阵的行列式；tr(·)为矩阵的迹；v为Wishart分布的自由度；W∈RM×M为Wishart分布的尺度矩阵。

假设噪声矩阵E的每一个元素是独立同分布的随机变量并且服从均值为零、方差为γ-1的高斯分布。为了学习γ，将Gamma超先验添加到γ之上，因此有

p(γ)=Gamma(γ|a,b)=Γ(a)-1baγa-1e-bγ

(5)

2.2 变分贝叶斯方法

在概率模型中，令y为观测数据，θ{X，Σ，γ}为所有的隐变量。变分贝叶斯的基本原理是通过最大化边际似然下界来获取p(θ|y)的近似后验分布q(θ)。其中边际似然下界定义为

(6)

根据文献[16]，假设q(θ)可以按照其组成变量θ分解，即存在如式(7)的表示形式，即

q(X，Σ,γ)=qx(X)qΣ(Σ)qγ(γ)

(7)

通过这样的分解形式，可以很方便地采用交替更新的方式来最大化边际似然下界L(q)。因此有

(8)

式(8)中：c为归一化常数，用来保证式(8)左边的函数成为一个积分为1的概率密度函数。详细的贝叶斯推理过程如下。

2.2.1 更新qx(X)

计算qx(X)的过程可以分解为计算矩阵X的每个列xn的近似后验分布，即qx(xn)。而qx(xn)的近似后验分布计算公式为

lnqx(xn)∝〈ln[p(yn|xn)p(xn|Σ)]〉qΣ(Σ)qγ(γ)∝

(9)

式(9)中：yn为矩阵Y的第n列；On为矩阵Ω的第n列；Ω为矩阵Y中非零元素的位置矩阵。可以看出，xn服从高斯分布，即

qx(xn)=N(xn|μn,Qn)

(10)

式(10)中：μn=〈γ〉QnOnyn，Qn=(〈γ〉On+〈Σ〉)-1。

2.2.2 更新qΣ(Σ)

qΣ(Σ)的近似后验分布可以通过式(11)来获得，即

〈XTX〉)Σ]

(11)

因此，Σ服从Wishart分布，即

(12)

(13)

(14)

(15)

2.2.3 更新qγ(γ)

通过对qγ(γ)变分优化得到，即

lnqγ(γ)∝〈lnp(Y|X,γ)p(γ)〉qx(X)∝

(16)

式(16)中：ymn和xmn分别为矩阵Y和X的第m行第n列的元素；S为矩阵Y中元素值不为空的元素下标的集合；L为集合S中元素值不为空的元素数目。

因此，qγ(γ)服从Gamma分布，即

(17)

(18)

(19)

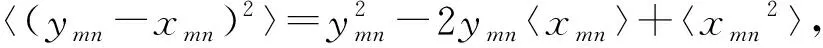
2.3 广义近似消息传递

广义近似消息传递是由循环信念传播框架发展而来的一种低复杂度的算法，其通过中心极限定理来有效地计算后验分布的近似估计，可以将信号的后验概率密度函数分解为简单的概率密度函数。因此广义近似消息传递可以从观测值y中得到xn的后验分布近似估计。

根据文献[14]，广义近似消息传递主要存在两个重要的近似：

近似一在输入端通过式(20)来近似真实后验分布p(xm|y)，即

(20)

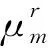
近似二在输出端通过式(21)近似真实后验分布p(zi|y)。公式为

(21)

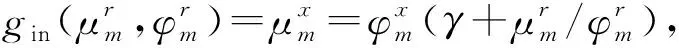
根据文献[14]，广义近似消息传递迭代的详细步骤如下：

(1)对于任意的i∈{1,2,…,M}，计算

(22)

(23)

(24)

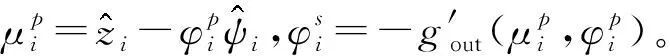
(2)对于任意的m∈{1,2,…,M}，计算

(25)

(26)

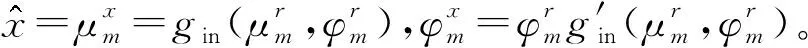
Rangan等[17]研究了在GAMP算法中加入阻尼的步骤保证算法的收敛性，因此在本文算法中也加入阻尼运算，公式为

(27)

(28)

(29)

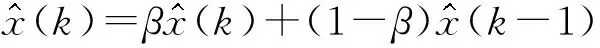
(30)

式中：阻尼系数β的取值范围是0<β<1。

2.4 算法总结

现将提出的基于低秩矩阵填充的推荐算法步骤总结如下：

算法:基于低秩矩阵填充的推荐算法Input: rating matrix Y∈RM×N, relative error ε, maximum iterations KOutput: the predicted rating matrix X∈RM×N1: Initialize parameter a,b,β,v,W and γ;2: Σ←(Y YT)/N+I;3: for k=1 to K do4: compute qx(X) by using the damped GAMP;5: update Σ using Eq.(12);6: update γ using Eq.(17);7: if x(k)-x(k-1)F/x(k)F<ε8: then stop9: end for10: return X

3 实验

3.1 实验数据集与评估方法

为保证实验结果的可比性，实验采用推荐系统研究中常用的MovieLens 100k数据集[18]，该数据集包含了10万条取值范围在1～5的整型评分数据，这些评分数据是943名用户对1 682部电影的评分记录。因此这些评分数据可以组成一个943行 1 682列的评分矩阵。

平均绝对误差(mean absolute error，MAE)和均方根误差(root mean squared error，RMSE)是推荐领域常用的检验算法性能的评估方法。本文实验采用MAE和RMSE作为评价标准。

MAE的定义为

(31)

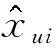
RMSE的定义为

(32)

从定义来看，这两种指标都是通过计算预测的评分值和实际的评分值之间的误差来度量推荐算法的性能。MAE和RMSE小，意味着该算法的预测精度高，推荐性能好。

3.2 实验结果及分析

算法中参数设定为：a=b=10-6，β=0.9，v=γ=1，W=10-10I，I为单位矩阵，ε=10-5。

第一个实验考虑迭代次数对实验结果的影响。图1所示为本算法在迭代学习过程中评价标准MAE和RMSE随着迭代次数的增大而逐渐下降的变化趋势。实验结果表明，在迭代次数多于1 400后，MAE为0.725左右，RMSE为0.925左右，MAE和RMSE开始收敛并逐渐趋于稳定，即评分预测的准确性趋于稳定。

图1 迭代求解RMSE收敛走势图Fig.1 Convergence tends of RMSE over iterations

第二个实验是为了比较本文算法的性能，选择了近年来提出的层次矩阵分解(hierarchical matrix factorization，HMF)算法[19]、多重图正则化矩阵填充(multiple graphs regularized matrix completion，MGRMC)算法[20]作为对比算法。HMF算法使用非负矩阵分解作为基本模型，同时利用了用户和项目的显式反馈和隐式反馈构成一种分层结构，解决了单一使用隐式反馈方法的不足。MGRMC算法建立矩阵的行和列的多图关系，将单一图正则化矩阵填充技术扩展到多重图正则化矩阵填充，使得算法效果优于单一图正则化矩阵填充。实验的结果如表1所示。

表1 三种算法的实验结果对比Table 1 Comparison of experimental results of three algorithms

由表1中三种算法的实验结果对比可以看出，本文提出的算法在MovieLens 100 k数据集上的MAE和RMSE都是最低的，说明本文算法效果优于其他两种对比算法。相较于HMF算法，本文算法的MAE和RMSE分别降低了3.33%和3.85%；相较于MGRMC算法，本文算法的MAE和RMSE分别降低了1.36%和1.07%。

4 结论

提出了一种基于低秩矩阵填充技术的推荐算法，通过采用分层高斯先验模型，促进矩阵的低秩性，基于这一模型使用变分贝叶斯方法完成矩阵填充，并在广义近似消息传递中加入阻尼步骤。通过实验证明该算法在预测用户评分的精度上胜于基于图正则化矩阵填充的方法和层次矩阵分解方法，能够进一步提高推荐算法性能。