三点圆法参数自适应插补算法

曹智梅

（广东松山职业技术学院，广东韶关 512126）

0 引言

普通数控机床具备直线和圆弧插补功能。对于非圆曲线的加工，通常是在曲线上取若干个点，在保证插补误差的前提下，两相邻点间采用直线的方式进行插补，这种插补计算方便，数学处理简单，但所得的逼近点数量较多，逼近线段较短，且各直线段连接处存在尖角，影响零件的加工质量。随着科技的进步，数控系统计算能力的增强，社会对数控加工产品的质量要求越来越高，圆弧插补得到了更广泛的应用。

圆弧插补就是在插补误差允许的范围内，用无数条微小的圆弧段来替代非圆曲线。采用微小圆弧段进给时，要解决各段圆弧尺寸的计算，以及圆弧顺逆的判断，以便使用系统已有的G02/G03指令来加工。与直线插补相比，圆弧插补能减少插补的段落数，提高插补质量。

采用圆弧段逼近曲线，目前常采用的方法有三点圆法、曲率圆法、相切圆法［1］等。其中曲率圆法的本质是二点圆法，其计算过程中涉及到四次方程的求解，计算复杂。而相切圆法虽然加工出的零件表面质量好，但整个计算过程非常复杂，同时要将曲线的拐点作为计算单元的分割点，增加了数控编程的难度。

三点圆法是在非圆曲线上按一定规律取3个已知点，根据三点定圆的原理计算圆弧的基本尺寸，再通过控制最大插补误差来修正插补点的位置。本文对传统三点圆法进行了改进，以参数中间点替代极值点［2］，简化三点圆法插补误差计算，在满足加工质量的前提下，其计算过程简便，插补效率高。

1 圆弧计算及顺逆判断

1.1 圆弧计算

三点圆弧计算如图1所示。

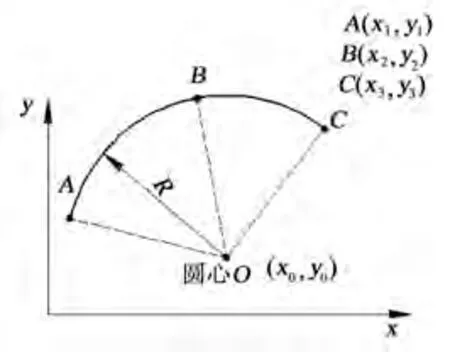
图1 三点圆弧计算

已知A（x1，y1）、B（x2，y2）、C（x3，y3）为圆上的三点，假设圆心坐标O（x0，y0），圆弧半径为R，如图1所示，则根据圆的特性可知，AO=BO=CO=R。则有：

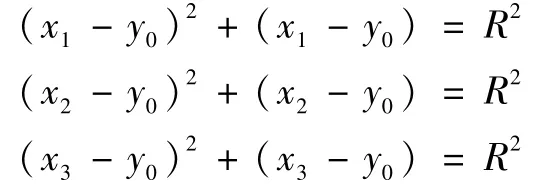
分别将3个方程式展开：

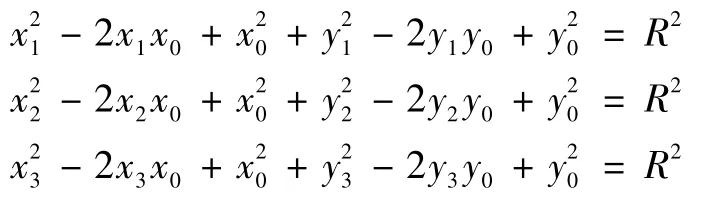
将方程两两相减，并令：

若D=0则：

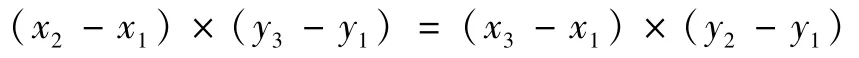
即A、B、C三点共线或有两个点重合或三点重合。

当D≠0可解得：

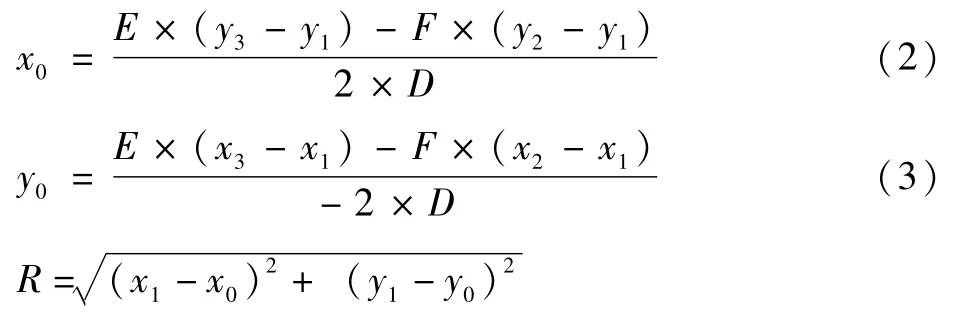
1.2 圆弧顺逆判断方法

在数控机床中要编写通过三点的圆弧程序，除了要计算圆弧的圆心坐标和半径，还必须判断出圆弧是顺时针还是逆时针，从而决定程序中采用G02还是G03。顺（逆）时针圆弧如图2所示。图2（a）～（b）的两段圆弧均通过A、B、C三点，其中A为圆弧的起点，B为圆弧的中点，C为圆弧的终点。

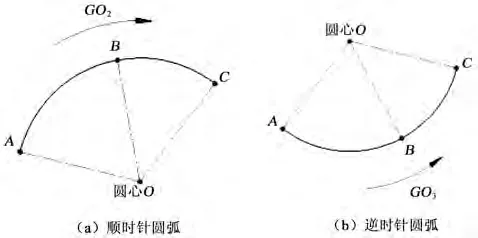
图2 顺（逆）时针圆弧

可以很直观地看出，对于图2（a），当点A绕着圆心经过点B到达点C，即AO经过BO到达CO时，其旋转的方向与时钟的转动方向相同，即为顺时针圆弧，同理，对于图2（b）则为逆时针圆弧。

在进行程序编程时，由于在曲线上选用的三点是在动态变化的，无法采用这种直观的方法进行圆弧顺逆的判断，必须要找到一个条件来判断，而且这个条件是可以用公式进行量化，通过量化的结果进行判断，并且判断的结果是唯一。

李柯等［3］介绍了采用角度的正切来判断圆弧顺逆，这种方法没有考虑到角度正切无意思的情况，且整个判断过程复杂，计算难度大。与之相比，利用向量叉积来判断圆弧的顺逆是一个比较好的选择。

1.3 向量叉积含义

两个向量的叉积为一个新的向量。根据定义，两个向量的叉积大小等于这两个向量组成的平行四边形的面积，其方向垂直于两个向量所决定的平面，其指向按右手定则从第一个向量转向第二个向量。当向量叉积为负时，表示从第一个向量旋转到第二个向量是顺时针；当向量叉积为正时，表示从第一个向量旋转到第二个向量是逆时针。

向量的叉积对圆弧的顺逆判断有一个很好的提示，如图3所示。图中，三点圆弧中的起点A和中点B两点构成的向，起点A和终点C两点构成的向量对于图3（a），按右手定则，向量的指向为垂直于当前平面指向屏幕内部，即向量叉积为负值，对照图2可知，此时圆弧为顺时针；对于图3（b），按右手定则，向量的指向为垂直于当前平面指向屏幕外部，即向量叉积为正值，对照图2可知，此时圆弧为逆时针。

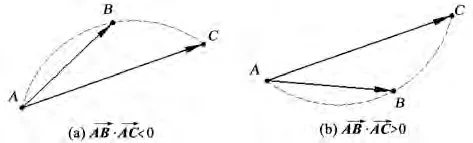
图3 向量叉积的正负

1.4 圆弧顺逆判断条件

已知A（x1，y1）、B（x2，y2）、C（x1，y1）三点，则向=（x2-x1，y2-x1），=（x3-x1，y3-x1），向和向的叉积为2×2的行列式，则：

利用右手法则进行判断：

2 三点圆法插补误差计算

插补算法的原理就是通过控制最大插补误差来完成插补点的筛选，所以插补误差的计算是整个插补算法的核心［4］。

2.1 两点间的距离公式

若已知A（x1，y1）、B（x2，y2）两点，则两点间的距离d可用公式表达为

2.2 插补误差算法原理

插补误差算法原理如图4所示。

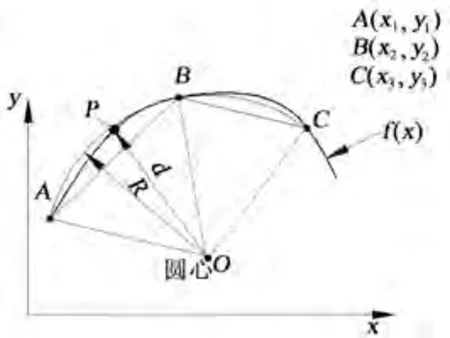
图4 插补误差算法原理

在要加工的曲线f（x）上依次取三点A、B、C，过三点作圆弧，圆弧的圆心为点O，圆弧的半径为R，则AO=BO=CO=R。设P为曲线上从A到C间的任意一点，P到点O的距离为d，即d=PO。则曲线f（x）在AC间的插补误差δ可表示为δ=|d-R|，最大误差为：

式中：最大误差δmax即为插补误差。若在式中，A、B、C三点坐标已知，则R为常数，求δmax则转化为求d的极值，即点P到点O的极值距离，由于点P为曲线上AC间的任意一点，求的极值即为求点O到曲线f（x）（x∈［x1，x3］）的最大（或最短）距离。

2.3 点到曲线极值距离的求解

求点到曲线的极值距离，就是求点到曲线的最大（或最短）距离。可采用二元函数条件极值的拉格朗日乘数法，再比较边界点到原点的距离，这些点也就是要找的极值点。

这种计算点到曲线极值距离的方法虽然比较精确，但计算过程较复杂，涉及到格朗日函数的构建以及偏导数的求解，且对于若干段微小圆弧插补来说，此种方法也不便采用。

2.4 插补误差简化算法（一级简化）

求解点到曲线的极值距离相对复杂。换一种思路，如果将该段曲线离散点的数量取成有限点，求各离散点到圆心的距离，并找出各距离中的极值，由于此段圆弧是微小段，所取点的数量不必多，甚至仅取少数几个点即可满足误差精度计算要求。

图5 插补误差简化算法

插补误差简化算法如图5所示。在曲线f（x）上，依次取A（x1，y1）、B （x2，y2）、C （x3，y3）。由于所取的三点A、B、C既在圆弧上，又在曲线上，因此该三点对应的插补误差为0，误差的极值点在AB间，或BC间。为求极值，将AB间和BC间分别将参数进行n等分，即AB间和BC间各取n-1个点，AB间每相邻的两个点间的参数增量为间每相邻的两个点间的参数增量为，设AB段中的第i个点为Hi，则Hi（xhi，yhi）坐标为：

设BC段中的第i个点为Ki，则Ki（xki，yki）坐标为：

则点Hi和Ki到圆弧圆心点O（x0，y0）的距离分别为：

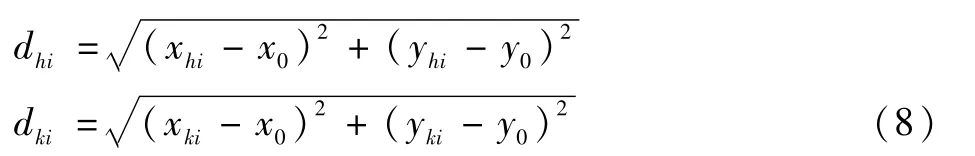
当i的取值从1到n-1时，计算每个对应的点Hi和Ki到圆心的距离，找出其极值点，即求出插补误差δh和δk，若整个圆弧段的允许插补误差为δ允，则：

设曲线f（x）的允许插补误差为δ允，通过比较δh、δk、δ允三者的大小，可以实现参数自适应的插补算法。当时δh≤δ允且δk≤δ允，直接进入下一段圆弧的插补，否则减少A、B、C三点间的参数增量，重新计算。

2.5 插补误差的实用简化算法（二级简化）

上述求δh和δk计算中，分别将AB和BC进行参数n等分（n≥2），n取得越大，则计算精度越高，但带来的问题是计算量成几何级数增加。

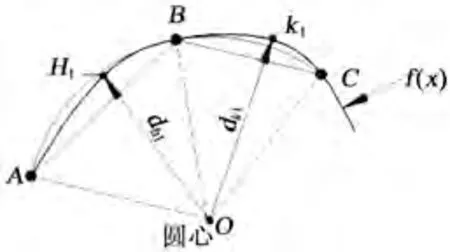
图6 插补误差实用简化算法

在实际加工中，为了简化计算，可以将n取最小值2（此时i=1）。如图6所示，此时仅在AB和BC段分别进行参数二等分，即在AB和BC两段各取一个参数中间点H1和K1，并将H1和K1作为误差的极值点。分别用两点间的距离公式计算H1和K1到圆心的距离dh1和dk1，此时δh=|dh1-R|，δk=|dk1-R|。

3 三点圆法参数自适应插

3.1 插补算法的参数表达

与一般的曲线方程相比，参数方程具有更好的计算特性，为了方便计算，通常要将曲线方程y=f（x）改写成参数方程的形式，即：

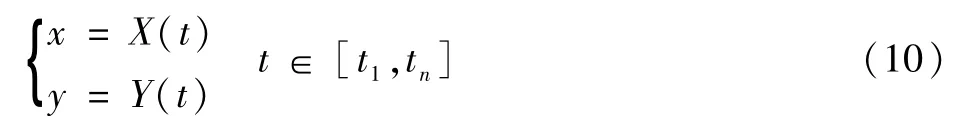
在曲线上依次取A、B、C三点，若A、B、C点对应的参数分别为t1、t2、t3，为了计算方便，令，即三点按等参数Δt的方式进行选取。

AB和BC段的参数中间点H1、K1对应的参数分别为：

求出H1和K1两点的参数就可以求出两点的坐标：

通过两点的坐标，分别计算点到圆心的距离，并计算δh和δk，比较δh、δk和δ允三者的大小关系。当δh、δk在允许的误差范围内时，继续进行下一段圆弧的插补；当δh、δk不同时满足插补误差条件时，则重新取点进行插补运算，直至圆弧插补满足误差条件为止。

3.2 算法流程框图

在设计算法流程框图时，把参数作为变量，通过控制插补误差来修正插补参数，通过参数的改变来不断重新选取插补点，直至插补结束。

首先按等参数Δt的方式在曲线上取A、B、C三点，并计算三点的坐标。

再接下来，计算圆弧的圆心坐标O（x0，y0），圆弧的半径R，计算参数中间点H1和K1的坐标，计算H1和K1到圆心的距离以及δh和δk。

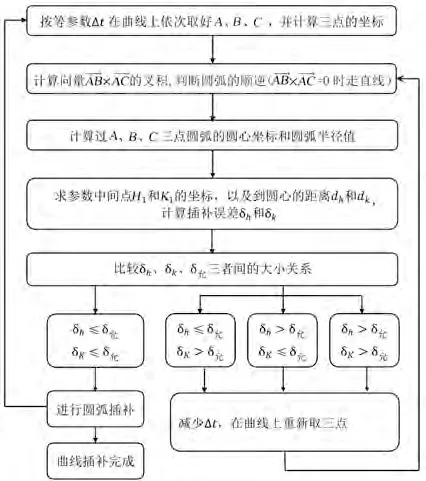
图7 三点圆法插补算法流程

比较δh、δk和δ允三者的大小关系。当δh≤δ允和δk≤δ允同时满足时，继续进行下一段圆弧的插补；不同时满足时，减少参数增量Δt，重新取A、B、C三点进行运算，直至满足误差许可条件为止。图7所示为三点圆法插补算法流程。

4 插补应用实例

4.1 加工椭圆曲线

椭圆曲线在实际中应用广泛，数控考证和数控大赛中常有涉及。若要加工的椭圆曲线方程为为方便各点的坐标计算，将椭圆的标准方程转化为参数方程：。设加工的起点为（50，0），根据三点圆法参数自适应插补算法原理，编写宏程序O0001［5］，如表1所示。

表1 宏程序O0001

续表

4.2 插补算法分析

为了更好地分析插补算法效果，将程序O0001导入数控仿真软件进行验证。由于椭圆为轴对称图形，故只验证t∈［0，90］的区间，即第一象限。其验证的加工轨迹如图6所示。

在进行编程时，只控制了最大插补误差，而没有限制最小插补误差，所以在实际加工中，参数增量的选取对插补过程有着一定的影响。在程序O0001中，分别增加3个变量，一个计算插补的圆弧段数，一个计算最大插补误差，一个计算最小插补误差，并将3个变量最终以坐标的形式输出。在进行插补时，初始设置的参数增量会对插补计算产生影响。表2所示为对Δt=2、Δt=4、Δt=6、Δt=10、Δt=12参数增量情况进行的误差统计。

图6 第一象限椭圆仿真加工轨迹

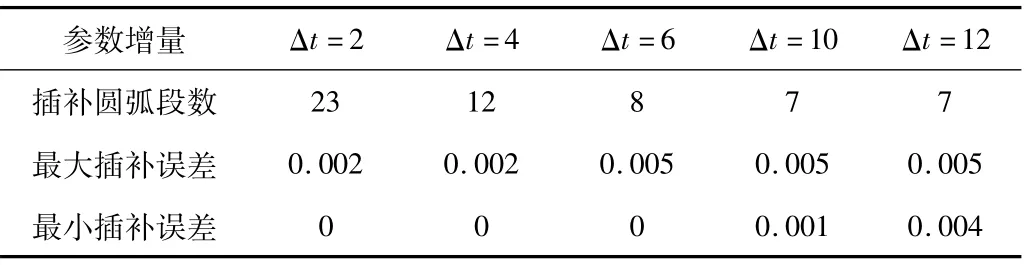
表2 参数增量对插补的影响

从表2可以看出，随着参数增量的增加，插补所需要的圆弧段逐渐减少，最终趋于恒定，当插补参数增量较小时，其最大插补误差小于允许误差，其插补的圆弧段数量增多，插补质量相对较好，但插补时间较长。

当参数增量的增加时，最大插补误差也增大，最终趋于恒定值0.005（插补允许误差，由程序来控制），所以也可以看出，参数增量的改变不会改变最大插补误差，从而也验证了该算法的正确性。但最小插补误差也始终小于最大插补误差，所以整个插补范围内都满足插补误差要求。当然，合理选择参数增量的大小可以减少插补圆弧段数，减少插补时间，提高插补效率。

将程序输入数控机床进行加工，加工出的产品也满足插补误差条件，进一步验证了算法正确性。

5 结束语

本文在研究圆弧插补的基础上，提出三点圆法参数自适应插补算法，主要研究工作有：

（1）已知圆弧上的三点，计算出圆弧圆心的坐标和圆弧半径，并分析出三点共线的情形；

（2）利用向量的叉积来判断圆弧的顺逆，并推导出判别公式，该判别方法简单，通用性强；

（3）分析三点圆法插补的误差计算原理，以参数中间点替代极值点来计算插补误差，简化计算过程，在插补过程中，合理选择参数增量的大小，可以提高插补效率；

（4）提出三点圆法参数自适应插补算法，给出了算法的插补原理和算法流程图，该算法能应用于抛物线、双曲线、正弦曲线、椭圆等多种非圆曲线，通用性强，与文献［6］的方法相比，具有更好的算法优势；

（5）以椭圆曲线的加工为例，给出了三点圆法参数自适应插补算法的完整程序，并在仿真软件和机床上验证了算法的正确性和适用性。