含末端质量的悬臂梁随机非线性振动的随机平均法

解娜娜， 葛 根

(天津工业大学 机械工程学院，天津 300387)

悬臂梁作为一种应用广泛的基础性结构，其动力学问题一直是学者们研究的重点。Zavodney等[1-2]进行了含集中质量的悬臂梁振动试验，在试验测试的基础上，采用多尺度法进行了理论分析，并用试验数据验证了分析的正确性。Nayfeh等[3]讨论了几何非线性和惯性非线性对响应的影响是否等效，在多尺度法的基础上，得出了几何非线性产生渐硬效应、惯性非线性产生渐软效应的结论。Dwivedy等[4]将多尺度法推广到高阶多尺度法，并将其应用于悬臂梁的动力学研究。Hamda等[5]比较了多尺度法和谐波平衡法的精度。悬臂梁振动常用的方法除了多尺度法外还有许多其它的方法，比如能量平衡法和变分法[6-7]， Nikkar等用这些方法研究了带有中间集中质量的均匀悬臂梁的大振幅自由振动。除此之外，学者们将激励从确定的简谐激励推广到随机噪声，如Feng等[8-9]用窄带噪声激励悬臂梁模型，并用多尺度法进行分析。Ge等[10]将随机平均方法应用于受高斯白噪声横向激励的悬臂梁模型。

在许多悬臂梁振动试验研究中，需要将附着在悬臂梁上的加速度传感器视为不可忽略的集中质量。由于振动过程中的横向和轴向都有位移，不可避免地在方程中产生惯性非线性项(在部分文献中称之为和坐标相关的质量coordinate-dependent mass)[11-12]，但是传统的随机平均法[13-15]只能解决拟线性振子或含有刚性非线性项的振子。当含有惯性非线性项时，现有的随机平均法尚不能完全适用。所以本文提出了一种可适用于含末端质量悬臂梁振动的改进强非线性随机平均法，这种方法将原本解决仅含有刚性非线性项的随机平均法扩展到了能解决既含有刚度非线性又含有惯性非线性的振子。

文中首先用凯恩方程对含有末端质量块的悬臂梁进行了建模，将模型的系数与Zavodney等用牛顿力学建立的含集中质量的模型系数进行了比较，发现当把文献[16]162中的边界条件改为与本文相同时，模型系数是相同的，这一比较证明了我们建模的正确性。然后构造了振子的哈密尔顿函数，利用该函数导出了关于瞬时振幅和瞬时相位的一组随机微分方程，随后用能量平衡法[17]得到了平均化频率表达式。本文的随机平均法将随机微分方程组简化为一维伊藤随机微分方程。基于伊藤方程，得到了末端质量取不同值时的瞬态振幅的稳态概率密度以及速度-位移的稳态联合概率密度。蒙特卡罗法数值模拟充分说明了本文方法的有效性。

1 建 模

图1 基座激励下含有尖端质量的细长均匀不可拉伸悬臂梁

如图1所示，由于梁是不可拉伸的，微段P的位移矢量为

dP=ui+[w(s,τ)+h(τ)]j

(1)

P的轴向位移和Mt的轴向位移为

(2)

式中，ξ为s的形式变量。

对式(2)求时间的导数，得到P的速度vP和加速度aP为

(3)

(4)

同样地，尖端质量Mt的速度和加速度为

(5)

(6)

梁的弯曲变形能

(7)

其中的弯矩M

(8)

悬臂梁的i阶横向位移可以设为式(9)

wi(s,τ)=φi(s)qi(τ)

(9)

(10)

式(10)的边界条件为

将式(3)～(9)代入式(10)，得到式(11)

(11)

引入无量纲变换

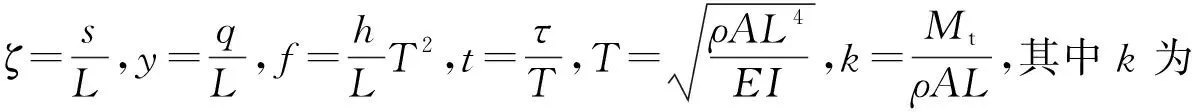
(12)

其中的系数为

模态函数是

φi(ζ)=cosh(λiζ)-cos(λiζ)+

(13)

式(13)虽然是由线性悬臂梁振动模型推导出来的，但在非线性动力学问题中仍是有效的。λi是超越频率方程式(14)的根。

kλ[cos(λ)sinh(λ)-sin(λ)cosh(λ)]·

[1+cos(λ)cosh(λ)]=0

(14)

表1 式(12)的系数

(15)

式(15)的系数,如表2所示。

表2 式(15)的系数

式(15)可被写为

(16)

式中：x为关于时间的t的变量，x的二阶导数前的括号内(1+α2x2)被称为惯性非线性项(坐标相关质量coordinate-dependent mass);α2为惯性非线性系数;α1为刚度非线性系数;ω为线性基础圆频率;μ为线性阻尼系数;γ为外激系数;η(t)为外激励信号。

当η(t)是高斯白噪声时，随机平均法是一种有效的求解方法。随机平均法有标准随机平均法(幅值包线随机平均)、能量包线随机平均[19]240-243等几种。Ge等曾利用能量平衡法改进了幅值包线随机平均法。这些随机平均法目前只能解决不含惯性非线性的振子的随机振动问题。为处理式(16)中惯性非线性，Ge等[20]采用一种近似变形：在式(16)上每项乘以(1+α2x2)-1，然后将(1+α2x2)-1用马克劳林展式近似为(1-α2x2)，如此这个方程被化简为形式上不含惯性非线性项的近似方程，随后该近似方程用随机平均法得以求解。文献[21]也采用类似泰勒展开的方法对加速度项进行的近似后采用路径积分法(path integral solution, PIS)求解含集中质量的悬臂梁响应的稳态概率密度函数数值解。Ge等提出的近似(1+α2x2)-1≈(1-α2x2)实际有很大的局限性，因为这个近似仅在x很小时才能成立。因此，目前需要一种能对式(16)直接求随机平均的方法。

2 公式变形

式(16)的动能为

(17)

式(16)保守力的势能为

(18)

则哈密尔顿函数为

(19)

假设位移、速度为

θ=Φ(t)+τ(t)

(20)

式中:A是随机瞬时等效振幅;τ(t)是随机相位。随机频率为

(21)

把式(20)代入式(19)，当θ=0，哈密尔顿函数为

(22)

当θ≠0，哈密尔顿函数为

(23)

显然处于稳态时，H1=H2在任何时候都成立，可以解得

(24)

其中

M(Acosθ)=1+α2A2cos2θ

(25)

我们现对x=Acosθ求时间导数得

(26)

化简得

(27)

再对y=-Aνsinθ求时间导数，结合式(25)中第二个式可得

(28)

(29)

(30)

(31)

如此联立式(27)和式(31)，并考虑

(32)

将式(32)代入式(27)，可得：

(33)

目前为止，我们已经将式(16)化为了式(32)、(33)这个随机微分方程组。

(34)

此结果已经被多次验证[22-23]。

如此，可知式(32)、式(33)中θ(t)可重新表示为

θ(t)=ω(A)t+τ(t)

(35)

3 随机平均

将式(32)、式(33)重新表示为标准形式

(36)

其中

(37)

首先式(37)这个结果中的漂移项m1，m2含有惯性非线性项M(Acosθ),而扩散项b11，b21则不含有，说明惯性非线性项只对漂移项起作用。其次，如果忽略惯性非线性，则式(37)就和文献[19]240-242中的表达式完全一致，这说明了上述的推导的正确性。如此可将式(36)用随机平均原理化简为一个一维伊藤微分方程。

dA=m(A)dt+σ(A)dW(t)

(38)

其中m(A)为漂移项，σ2(A)为扩散项，W(t)为标准的单位维纳过程。m(A)和σ2(A)表达式由式(39)得出

(39)

Rij(τ)=

(40)

其中的算子E[·]表示数学期望，δ(τ)为狄拉克-德尔塔函数。

由式(39)可以计算出m(A)和σ2(A)表达式分别如下

(41)

其中各系数为

a6=α1(3Dα1α2+40α1μω2+22α2μω4)

a4=4(5Dα1α2ω2+44α1μω4+8α2μω6)

a2=-4(Dα1ω2-4μω6)

a0=-8Dω4

(42)

4 稳态概率密度

基于伊藤方程的平均福克-普兰克-柯尔莫哥洛夫方程(Fokker-Planck-Kolmogorov, FPK)为

(43)

(44)

常数N是归一化系数。

只需把式(41)、(42)代入式(44)可得稳态概率密度函数式(45)

(45)

如此可知关于哈密尔顿函数H的稳态概率和振幅A的稳态概率密度关系如下

(46)

振幅A和哈密尔顿函数H的关系可由式(22)反解出来

(47)

只需把式(47)代入式(46)即可得到关于哈密尔顿函数H的稳态概率。

再接下来，关于x和y的联合概率密度又可以由哈密尔顿函数H的稳态概率得到

(48)

5 数值模拟

(实线：式(45)解析解；圆点：数值模拟)

关于位移x和速度y的联合概率密度函数的计算如下。先定义一个平面{-0.2≤x≤0.2,-0.6≤y≤0.6}，以步长Δx=0.013,Δy=0.04划分30×30网格。对刚才稳态的n=2 000×200 000个点统计落在每个格子里的点数，如此可计算出每个格子里的概率值，将概率值除以格子面积Δx·Δy即可得每个格子的概率密度函数值。理论值式(47)和其数值模拟的结果如图3所示。

(a) k=0,式(48)理论预测值

从图2、图3可以发现，无论是等效振幅A还是速度和位移联合概率密度的理论预测结果和蒙特卡罗数值模拟结果对应非常良好。这说明了本文方法的有效性。

6 结 论

本文研究了一种可应用于含有末端质量的悬臂梁振动的随机平均法，将原本只能处理含有非线性刚度的随机平均法发展到了能处理同时含有刚性非线性项和惯性非线性项的随机微分方程组，我们发现：

(1) 惯性非线性只影响随机微分方程的漂移项，不影响扩散项。

(2) 在微分方程组化简为伊藤方程后，在伊藤方程基础上，得到概率密度函数的表达式。数值模拟和概率密度函数的理论预测与模拟结果完美对应。

总的来说，本文方法有效地扩大了随机平均法的使用范围。