正则系对有局部单位半群的刻画
梁星亮 赵宪钟 任苗苗
(1. 西北大学数学学院, 陕西 西安 710127; 2. 陕西科技大学文理学院, 陕西 西安 710021)
1 引言
半群的分类问题是半群理论中的核心问题之一, 其中半群的S- 系理论是研究半群同调分类的一种有效方法. 20 世纪60 年代, 很多学者致力于幺半群同调分类问题的研究, 利用幺半群上系范畴中对象的性质刻画幺半群, 已有许多重要研究成果面世[1-10].幺半群上S- 系的正则性作为半群的von Neumann 正则性的一种重要推广, 从20 世纪80 年代开始备受学者们的关注. 1985 年, 文献[11] 首次在幺半群的S- 系范畴中引入了正则系的概念, 并利用S- 系的正则性给出了幺半群是群以及可消幺半群的刻画; 1995 年, 文献[12] 给出了所有正则左S- 系是平坦的幺半群的特征刻画; 2004 年,文献[13] 在幺半群的S- 系范畴中引入了正则系的一个推广, 称之为C(P) 系, 研究了与C(P)系有关的同调分类问题,给出了所有S-系具有C(P)性质,以及S-系的C(P)性质与其它平坦性质一致的幺半群的刻画; 2018 年, 文献[14] 在此基础上进一步做了推广, 引入了C(P′) 系, 并给出了幺半群是C(P′) 幺半群以及正则幺半群的特征刻画. 上述研究的主要对象是幺半群, 所考虑的范畴是幺半群上的系范畴. 众所周知, 更多半群并无幺元, 且许多幺半群的经典刻画对于不含幺元的半群未必成立. 基于此, 本文将有局部单位半群理论与幺半群理论的同调分类方法有机结合, 在有局部单位半群上的酉系范畴中引入正则对象, 通过研究正则对象的性质来刻画有局部单位半群的特征, 为不含幺元半群的同调分类研究提供新的思路.
2 预备知识
本文假设S是半群(未必含有幺元1),E(S) 表示S的所有幂等元构成的集合. 本节给出文中要用到的定义以及相关引理.
定义2.1[15]称半群S有局部单位, 如果对任意的s ∈S, 存在幂等元e,f ∈S使得es=s=sf, 同时称e是S的一个左单位元,f是S的一个右单位元.
显然, 幺半群、正则半群和富足半群都是有局部单位半群.
定义2.2[15]设S是半群,A是非空集合. 若有S×A到A的映射f:S×A →A满足
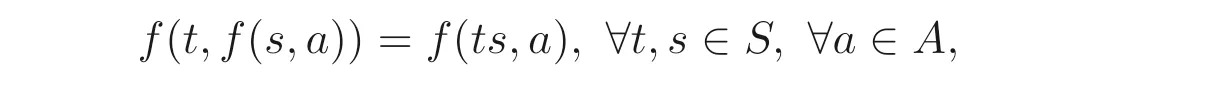
则称(A,f) 是左S- 系, 或称S左作用于A上. 为了方便起见, 记f(s,a)=sa, 于是上式变为
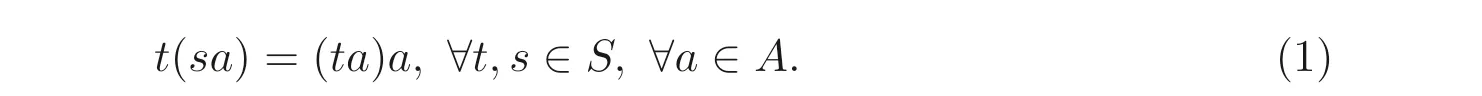
此时, 左S- 系(A,f) 简记为A或SA. 特别地, 当S是幺半群时, 如果映射f在条件(1) 基础上又满足1a=a, ∀a ∈A, 则称A是单式左S- 系.
定义2.3[15]设A,B都是左S- 系. 称映射f:A →B为从A到B的左S- 同态, 如果f(sa) =sf(a), ∀s ∈S, ∀a ∈A. 所有左S- 系以及左S- 系之间的S- 同态构成一个范畴, 称为左S- 系范畴.
定义2.4[15]设S是半群,A是左S- 系. 称A是酉S- 系, 如果SA=A. 所有的酉左S- 系和它们之间的S- 系同态构成左S- 系范畴的一个全子范畴, 称为酉左S- 系范畴.
下面给出有局部单位半群上酉系的一个重要性质.
引理2.1设S是有局部单位半群,A是酉左S- 系. 则对于任意元素a ∈A, 存在e ∈E(S), 使得a=ea.
证明对于任意元素a ∈A, 由A的酉性可知, 存在s ∈S,a′∈A使得a=sa′. 因为S是有局部单位半群, 所以存在e ∈E(S), 使得s=es. 因此,a=sa′=esa′=ea.
定义2.5[15]设A是右S- 系,B是左S- 系, 作卡氏积A×B, 令
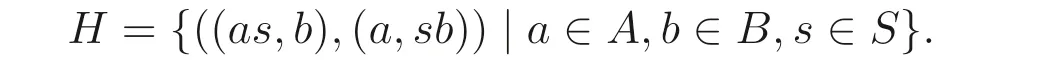
记ρ=ρ(H) 为由H生成的A×B上的最小等价关系. 称商集A×B/ρ为A和B的张量积, 记为A ⊗B, (a,b) 所在的等价类记为a ⊗b.
由定义2.5 以及等价关系的定义可得到A ⊗B中两个元素相等的具体刻画.
引理2.2设A是酉右S- 系,B是酉左S- 系,a,a′∈A,b,b′∈B, 则在A ⊗B中a⊗b=a′⊗b′的充要条件是存在a1,··· ,an ∈A,b1,··· ,bn ∈B,s1,t1,··· ,sn,tn ∈S,使得
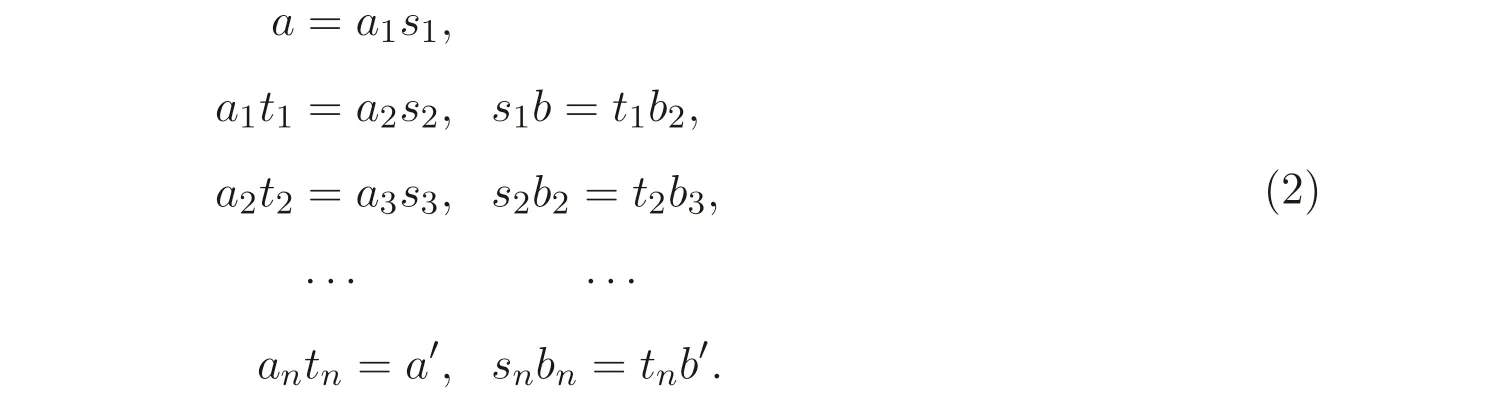
证明规定A×B上的关系σ如下: 对任意的a,a′∈A,b,b′∈B, (a,b)σ(a′,b′)⇔存在a1,··· ,an ∈A,b1,··· ,bn ∈B,s1,t1,··· ,sn,tn ∈S, 使得等式组(2) 成立. 下证σ是A×B上的等价关系.
因为S是有局部单位半群, 且A是酉S- 系, 所以对于a ∈A, 存在e ∈E(S), 使得a=a·e. 从而有a=a·e, a·e=a, e·b=b, 即(a,b)σ(a,b), 故反身性成立. 对称性显然. 下证传递性.
设(a,b)σ(a′,b′),(a′,b′)σ(a′′,b′′), 则对于a′∈A, 存在f ∈E(S), 使得a′=a′f. 从而有如下等式组:即(a,b)σ(a′′,b′′). 因此σ是等价关系.
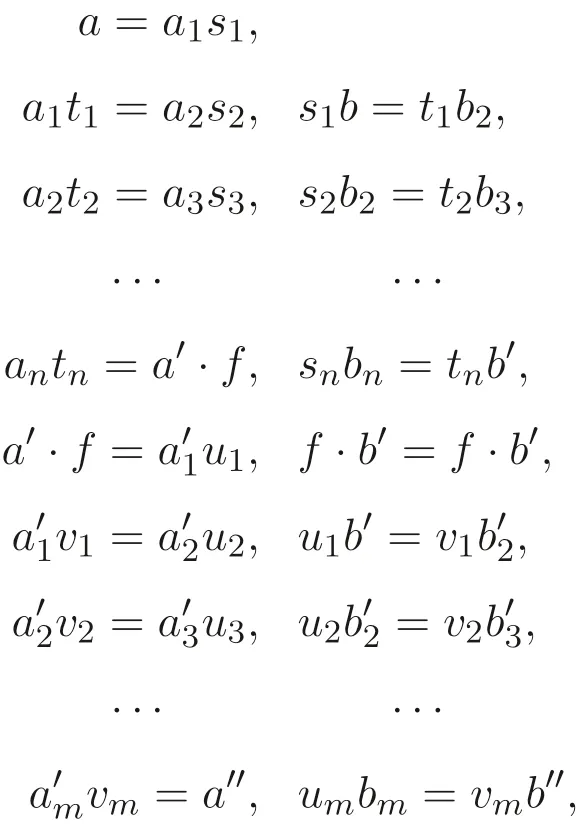
对于任意((as,b),(a,sb))∈H, 由于a ∈A, 所以存在e ∈E(S), 使得a=ae. 从而有
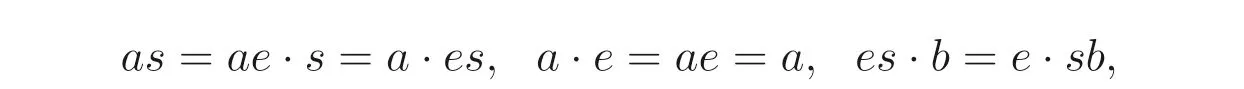
所以(as,b)σ(a,sb), 从而ρ ⊆σ.
设(a,b)σ(a′,b′). 则有
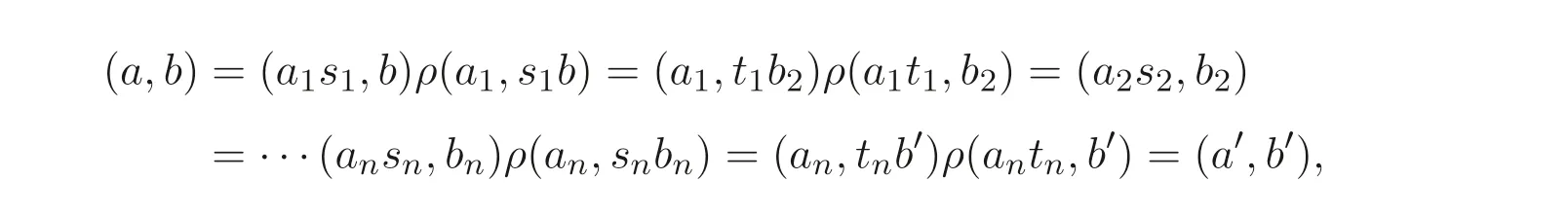
即(a,b)ρ(a′,b′), 所以σ ⊆ρ. 故由定义即得结论.
由文献[2] 知, 张量函子−⊗B把单同态不一定变为单映射. 因此, 引入了
定义2.6称左S- 系A是主弱平坦的, 如果对于S的任意主右理想I, 映射I ⊗A →S ⊗A是单的.
定义2.7[15]设S是半群, 称S- 系P是投射的, 如果对于任意S- 满同态φ:A →B, 任意S- 同态f:P →B, 存在S- 同态g:P →A使得f=φ°g.
如果半群S的任意主左理想是投射左S- 系, 则称S是左PP半群.
下面给出投射系的性质与结构刻画.
引理2.3[15]设S是有局部单位半群, 则左S- 系Se,e ∈E(S), 是投射的.
引理2.4[15]设S是有局部单位半群, 循环S- 系Sx是投射的当且仅当存在S的幂等元e, 使得Sx ≃Se.

下文除特殊声明以外, 半群均指有局部单位半群,S- 系均是酉左S- 系.
3 正则系
本节在酉系范畴中引入正则对象, 探讨它的基本性质, 给出正则对象中元素的等价描述, 揭示正则性与余直积以及正合序列之间的关系.
定义3.1设A是S- 系,a ∈A, 称a是A中的正则元, 如果存在S- 同态f:Sa →S, 使得f(a)a=a.
设S是正则半群,s ∈S, 则存在s′∈S, 使得ss′s=s, 作映射f:Ss →S为f(ts)=tss′. 容易验证f是左S- 同态, 且f(s)s=ss′s=s, 所以S是左S- 系中的正则元.
注3.1半群S中的正则元和左S- 系中的正则元是不一致的, 前者是指von Neumann 正则, 而后者是指定义2.1 意义下的正则.
下面给出S- 系中正则元的基本性质.
命题3.1设A是S- 系,a ∈A, 以下三条等价:
(1)a是A中的正则元;
(2) 存在e ∈E(S), 使得ea=a, 并且对于任意p,q ∈S, 若pa=qa, 则pe=qe;
(3)Sa是投射S- 系.
证明(1)⇒(2) 设Sa →S是S- 同态且满足f(a)a=a, 记e=f(a)∈S. 则
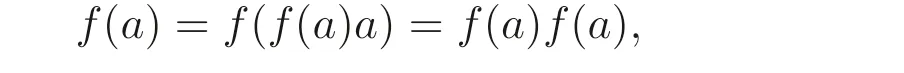
这说明e ∈E(S), 且ea=a. 假设p,q ∈S, 使得pa=qa. 则

(2)⇒(3) 定义映射φ:Sa →Se如下:
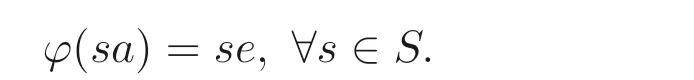
则由条件(2) 易知φ是有定义的. 若se=te, 则sa=sea=tea=ta, 这说明φ是单的. 易证φ也是S- 满同态, 因此φ:Sa →Se就是同构. 再由引理2.3 知,Sa是投射的.
(3)⇒(1) 设Sa是投射的, 根据引理2.4, 存在S- 同构g:Sa →Se, 其中e ∈E(S).设g(a)=s,g(ta)=e, 其中t ∈S, 则有
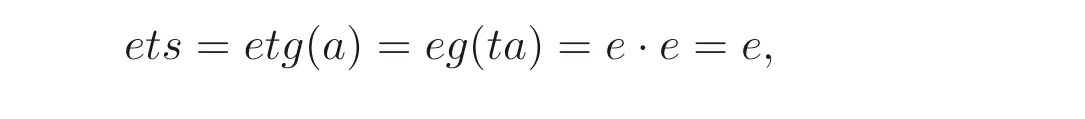
所以setset=seet=set, 即set ∈E(S). 令e′=set. 作映射h:Sa →Se′为h(xa)=xe′,x ∈S. 若xa=ya, 则xs=ys, 从而xe′=ye′, 说明h有定义. 而且对于任意的z ∈S, 有
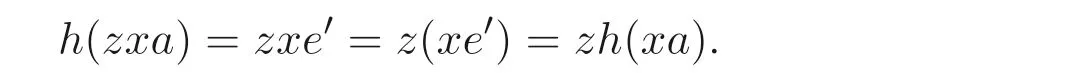
这说明h是S- 同态, 并且h(a)=e′, 这是因为对于a ∈A, 存在v ∈E(S) 使得a=va,从而有
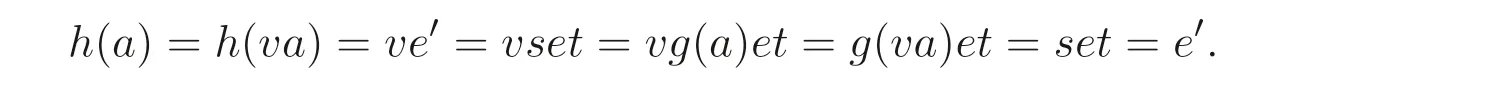
设xe′=ye′, 则
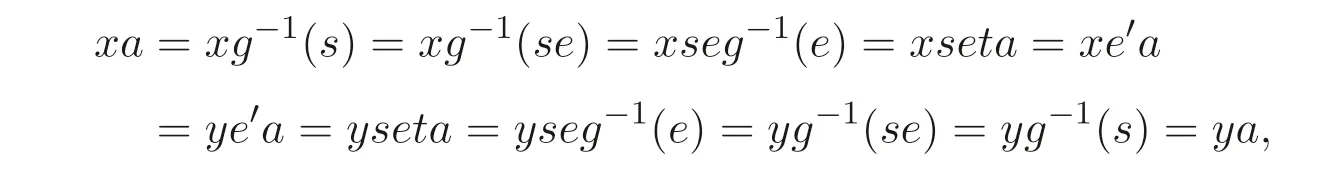
所以h是单的, 从而h是S- 同构. 由
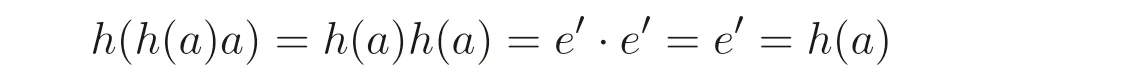
可推出h(a)a=a, 故a是A中的正则元.
定义3.2设A是S- 系. 如果A中的所有元素都是A的正则元, 则称A是正则S- 系.
命题3.1 的一个直接推论是
推论3.1S- 系A是正则的当且仅当A的任意循环子系都是投射的.
下面给出正则S- 系的例子.
例3.1(1) 若S是正则半群, 则S作为左S- 系SS是正则的.
(2) 设S是右可消半群, 则由命题3.1 的条件(2) 可知S是正则S- 系. 事实上, 由下面的命题3.2 可知此时任意投射S- 系都是正则的.
下面刻画S- 系的正则性与子系以及余直积之间的关系.命题3.2设S是有局部单位的半群. 则
(1) 正则S- 系的任意子系仍是正则系;
(2) 正则S- 系的余直积仍是正则系.
证明(1) 由正则系的定义以及命题3.1 可得.

下面命题说明S- 系的满同态保持正则性质.
命题3.3设S是有局部单位的半群, 是左S- 满同态, 若B是正则S- 系, 则A也是正则S- 系.
证明设a ∈A. 根据命题3.1, 存在e ∈E(S), 使得a=ea. 对任意p,q ∈S,若pa=qa, 则有pg(a) =g(pa) =g(qa) =qg(a). 因为B是正则的,g(a)∈B,且g(a)=g(ea)=eg(a), 所以由命题3.2 知pe=qe. 这说明a是正则元, 因此,A是正则S- 系.
根据命题3.3 和S- 系Rees 短正合序列的定义, 易得
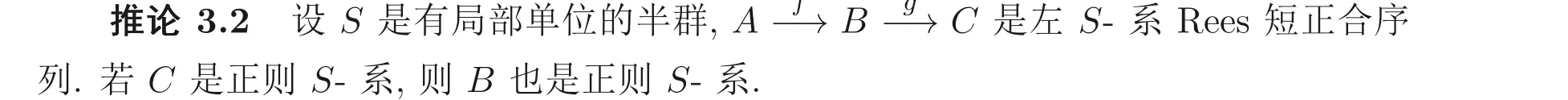
4 正则系对有局部单位半群的刻画
本节利用S- 系的正则性质对有局部单位半群进行同调分类, 给出所有正则系是主弱平坦的和投射的有局部单位半群的特征刻画. 为此, 首先给出
命题4.1若存在正则S- 系, 则S- 系中有一个最大的正则左理想.
证明设A是正则S-系,a ∈A, 则由命题3.1 知Sa是投射的. 根据引理2.4 有S-同构Sa →Se,e ∈E(S). 再由命题3.2 知Sa是正则S- 系, 所以Se也是正则S- 系,这说明S中有正则左理想.
令T为S的所有正则左理想的并, 则由命题3.2 也知T是正则的. 显然T是最大的正则左理想.
以下总是以T(S) 表示S的最大正则左理想.
下面通过研究S- 系的正则性与主弱平坦性之间的关系, 给出有局部单位半群的特征刻画.
定理4.1对于有局部单位半群S, 以下两条等价:
(1) 所有正则S- 系是主弱平坦的;
(2) 对于任意s ∈S, 任意的e2=e ∈T(S),se是S的von Neumann 正则元.
证明(1)⇒(2) 设s ∈S,e2=e ∈T(S). 如果Sse=Se, 则存在t ∈S, 使得tse=e, 所以se=setse, 即se是von Neumann 正则元. 下设Sse ̸=Se. 构造S-系M如下:
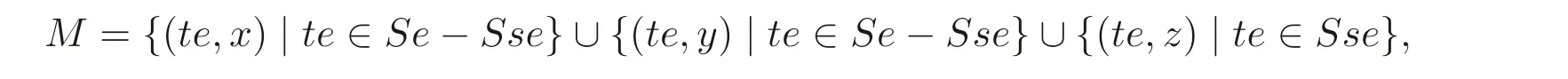
这里x,y,z是三个符号, 规定S在M上的作用为
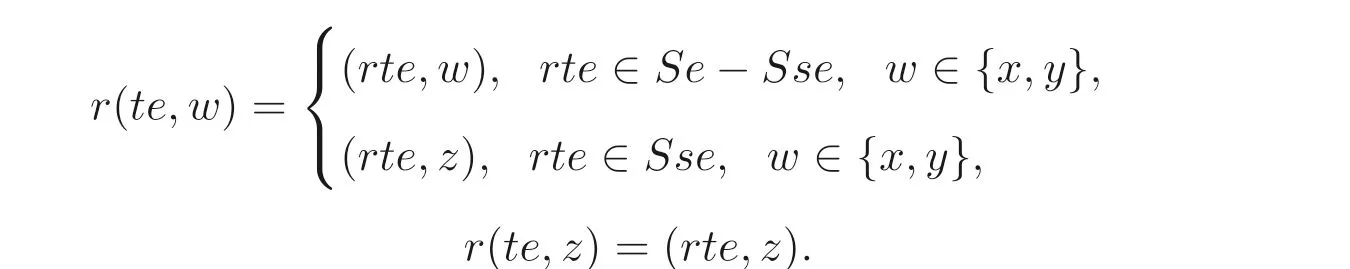
容易验证M按照上述定义构成一个左S- 系. 显然有S- 系同构S(e,x)≃Se ≃S(e,y).由于Se ≤T(S), 所以由命题3.2 知Se是正则系, 从而S(e,x) 和S(e,y) 是正则系. 再根据命题3.2,M=S(e,x)∪S(e,y) 是正则系, 从而由条件知M是主弱平坦的.
因为se(e,x)=(se,z)=se(e,y), 由M的主弱平坦性知在seS ⊗M中有
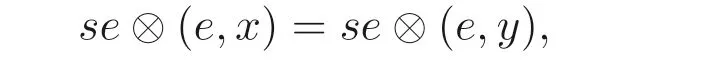

所以存在s1,t1,··· ,sn,tn ∈S,a1,a2,··· ,an ∈M,u2,··· ,un ∈seS, 使得设ai=(pi,wi),其中pi ∈S,wi ∈x,y,z. 由上述等式组可知存在某个i,使得tipi ∈Sse,从而有
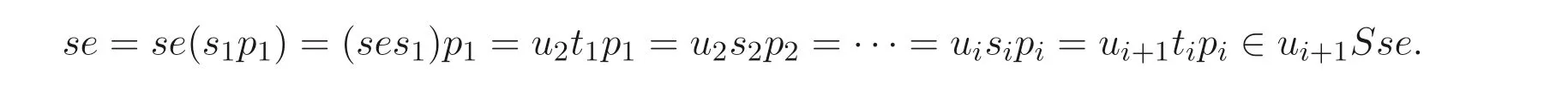
又因为ui+1∈seS, 所以se=seSse, 即se是von Neumann 正则元.
(2)⇒(1) 设A是正则S- 系,a,a′∈A,s ∈S, 在S ⊗A中有s ⊗a=s ⊗a′. 则由引理2.2 知, 存在a2,a3,··· ,an ∈A,s1,s2,··· ,sn ∈S,u1,v1,··· ,un,vn ∈S, 使得
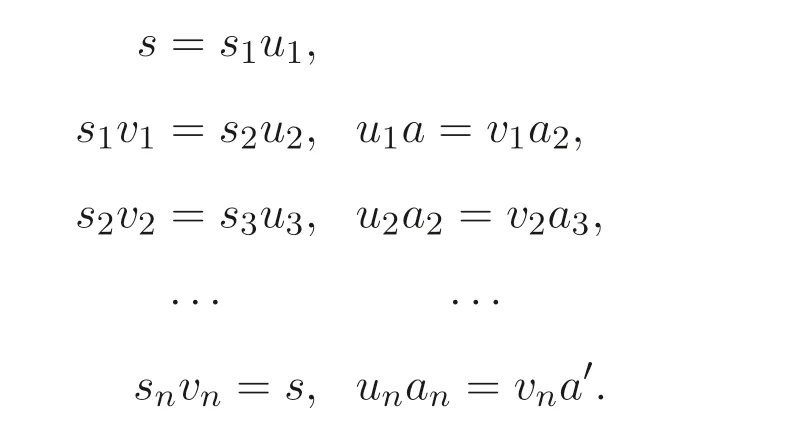
记a1=a,an+1=a′. 因为a1,··· ,an+1是A中的正则元, 所以由命题3.1 知, 存在e1,··· ,en+1∈E(S) 使得{a1,e1},{a2,e2},··· ,{an+1,en+1}是A的正则对. 因此有如下等式组
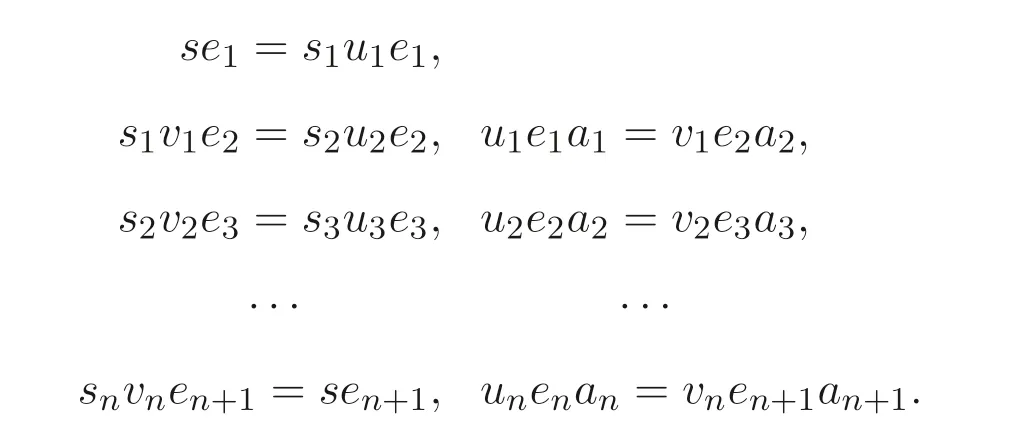
下面对n用数学归纳法, 证明在sS ⊗A中有s ⊗a=s ⊗a′.
设n= 1. 则有se1=s1u1e1, s1v1e2=se2, u1e1a=v1e2a′. 由命题3.2 的证明知Se1是正则左理想, 所以e1∈T(S). 由条件知u1e1是von Neumann 正则元, 故存在w1∈S, 使得u1e1=u1e1w1u1e1. 从而有
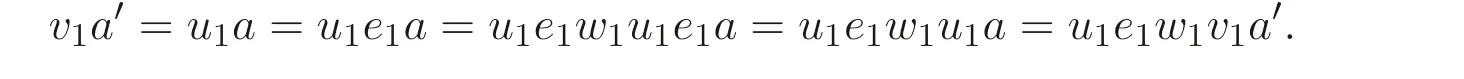
因为{a′,e2}是正则对, 所以有v1e2=u1e1w1v1e2. 因此, 在sS ⊗A中有

设n≥2. 因为Se1≃Sa1是正则系, 所以e1∈T(S). 因此存在w1∈S, 使得u1e1=u1e1w1u1e1. 从而有
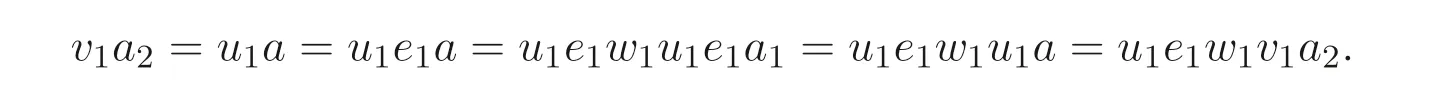
由于{a2,e2}是正则对, 所以有v1e2=u1e1w1v1e2. 因此,
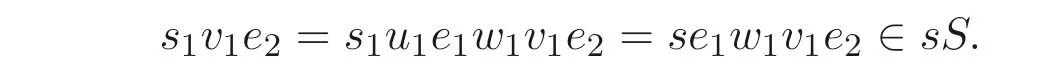
利用归纳假定知, 在sS ⊗A中有
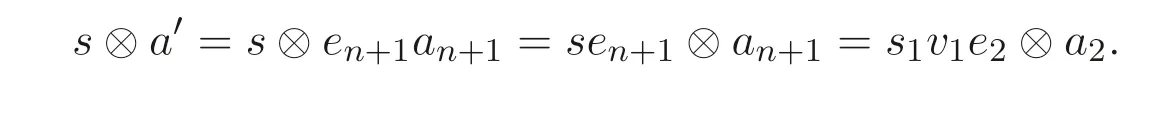
由于s2u2e2=s1v1e2∈SS, 再利用归纳假定可知, 在sS ⊗A中有
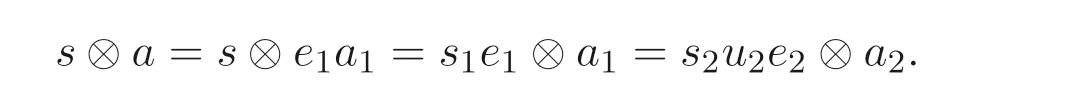
因此, 在sS ⊗A中有
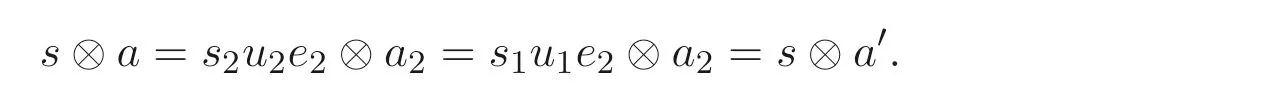
故A是主弱平坦的.
推论4.1对于有局部单位半群S, 以下两条等价:
(1)S是正则半群;
(2)S是左PP半群, 并且所有正则S- 系是主弱平坦的.
证明S是左PP半群当且仅当sS是正则S- 系, 当且仅当T(S) =S, 所以由定理4.1 即得本推论.
接下来通过研究S- 系的正则性与投射性之间的关系, 给出有局部单位半群的特征刻画. 为此, 先引入
命题4.2设A是有限生成S- 系. 若A是投射的, 则A是有限个循环子系的不交并.
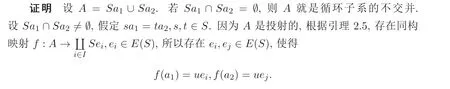
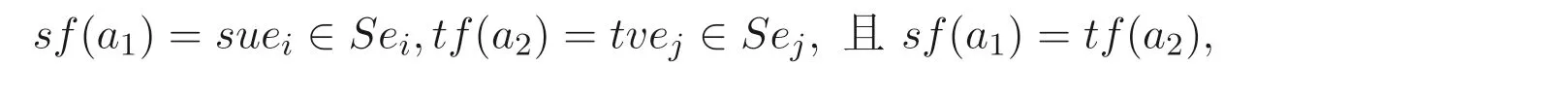
又因为所以i=j, 由A的结构可知,f−1(ei)∈Sa1或者f−1(ei)∈Sa2. 若f−1(ei)∈Sa1,则a2∈Sa1, 所以A=Sa1. 若f−1(ei)∈Sa2, 则a1∈Sa2, 从而A=Sa2. 因此,A是循环子系的不交并.
设A=Sa1∪Sa2···∪San, 利用数学归纳法, 类似于上面的证明即可得出结论.
下面给出所有正则系是投射的等价刻画:
定理4.2对于有局部单位半群S, 以下两条等价:
(1) 所有正则S- 系是投射的;
(2) 对任意e2=e ∈T(S),Se是S的极小左理想.
证明(1)⇒(2) 设e2=e ∈T(S). 则Se是S的左理想. 设I是S的左理想并且I ≤Se,I ̸=Se. 类似于定理4.1 的证明构造正则S- 系M, 由条件知M是投射的.由命题4.2 知M是循环子系的不交并. 但这是不可能的, 因为
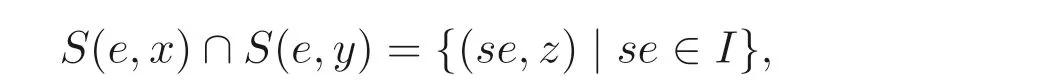
所以Se是极小左理想.
(2)⇒(1) 设A是正则S- 系. 则对任意a ∈A, 有S- 系同构Sa ≃Se, 所以Se是正则的, 从而e2=e ∈T(S). 由条件即知Se是极小左理想, 因此Sa是单S- 系, 即中Sa没有真子系. 容易证明A是若干个单子系的余直积, 而每个单子系是投射的, 所以A是投射的.

