Landau damping of twisted waves in Cairns distribution with anisotropic temperature

Sunggeun LEE and Hankwon LIM

School of Energy and Chemical Engineering, UNIST, 50, UNIST-gil, Eonyang-eup, Ulju-gun, Ulsan 44919, Republic of Korea

Abstract The consideration of orbital angular momentum of an electric field (twisted mode)is applied to the kinetic theory of plasma.The linearized Vlasov–Poisson equation is solved for the anisotropic thermal distributed bi-Maxwellian and Cairns distributions of electrons to obtain the damping rates of twisted waves.The dispersion relation and Landau damping of Langmuir twisted modes are obtained.The presence of twisted modes opens up two more possibilities in Landau damping and dispersion relations.This may generate a mixture with ion sound waves.It seems to play the role of a control parameter of Landau damping.

Keywords: Landau damping, Cairns distribution function, anisotropic

1.Introduction

The linearization of the Vlasov–Poisson equation may give a result of dissipation,even without a collision in plasma.It is a collisionless wave damping (because of the absence of collision) discovered by purely mathematical inspiration.This so-called Landau damping had been missed in the first observations of linearized equations, but Landau [1] found it through pure mathematical consideration.It is well known that both the dissipation and dispersion relations depend on the distributions of electrons,ions and dusts.Landau damping[1]for Langmuir oscillations[2]originates from an exchange in energy between waves and plasma particles characterizing collisionless plasmas.Coherent oscillations can decay exponentially and its experimental observation was reported in[3].It may be applied in galaxy formation, where stars can be considered as particles of plasma with gravitational interaction rather than electromagnetic ones.Spiral arms can be formed in the gas of stars due to instabilities, but Landau damping causes limitations in this process.There are collective oscillation modes in plasma that can be identified with Landau damping.It has been extended to non-Maxwellian particle distribution, background plasma non-uniformities,magnetic fields, multiple plasma species, nonlinear effects,and so on.

Landau damping can be seen in many areas of plasma physics: supplementary heating of magnetically confined plasma in fusion devices, in high-energy tail formations of particle distribution functions, in fast charged particle beam relaxation, in laser–particle interactions [4], in particle acceleration by means of plasma accelerators [5], for the heating of coronal gas [6] and for that of interstellar medium[7].Landau damping has applications in areas such as superfluids [8] and quarks [9] as well.Many of its basics are treated in [10].

The thermal Maxwellian distribution is an ideal distribution, but the distribution function deviates from the Maxwellian one in the real world.The existence of non-Maxwellian distribution of space plasmas from outer space observation has been confirmed with the properties of superthermal particles and anisotropy, such as solar corona,solar flares and solar wind particles [11, 12].Besides the active solar area,the magnetosphere[11,13]has also features of non-Maxwellian distribution.

The conditions for the existence of Landau resonance were established with the first introduction of its concept[14]and a detailed examination of Maxwellian plasma was performed.A study on the electrostatic ion waves for non-Maxwellian or Lorentzian distributed unmagnetized pair-ion plasma was conducted [15].Electron-ion-dust plasma for non-Maxwellian distribution (Lorentzian or kappa) showed the existence of the dust-acoustic mode[16].Landau damping in unmagnetized kappa distributed plasma composed of electrons and positively and negatively charged ions was studied in ion-acoustic waves [17].The Buneman instability affected by a nonthermal ion based on ion streaming was studied in Lorentzian dusty plasma[18].The growth rates and the real frequency term of the unstable root were shown to be suppressed by the nonthermal effect.Both numerical and analytical study on the three-dimensional Cairns and Kappa–Cairns distribution functions were implemented in [19].

We consider Landau damping in the presence of electrostatic orbital angular momentum (OAM).The angular momentum of an electromagnetic wave consists of an intrinsic part (spin angular momentum (SAM)) and an extrinsic part OAM).Extensive studies on OAM can be found in [20].In a laser beam the paraxial approximation of OAM is interpreted as Laguerre–Gaussian distribution[21].Based on the OAM of propagation of photons through random aberrations on coherence, rotational coherence function is derived [22].As three exact eigenmodes with OAM,photons,phonons and plasmons were studied in [23].The nonparaxial form of OAM was studied in [24].Various related works on plasmas have been carried out [25–28].The instabilities coming from stimulated scattering of coherent circularly polarized electromagnetic waves with OAM were studied in[29]and OAM helped form a tornado-like structure [30].The OAM exchange between electromagnetic and electrostatic waves in plasma [31] can be induced by stimulated Raman and Brillouin backscattering.The possibility of twisted dust-acoustic waves of a vortex beam carrying OAM was discussed in [32].

Astrophysical application of OAM based on the new development of the measurement of OAM with limitations was discussed in[33].The astronomical application following astronomical observables was studied in [34] suggesting calculus tools.The generation of OAM by rotating black holes [35–37] and gravitational waves [38] was studied.

Various types of electromagnetic instabilities can arise in a uniform plasma by anisotropy as an average of kinetic energy.Electron anisotropic velocity distribution can drive such an instability, e.g.Weibel instability [39].In unmagnetized plasma, Weibel instability with a non-Maxwellian distribution function was discussed [40].Weibel plasma instability has a wide range of applicability [41].

Landau damping of dust-acoustic waves in general(α,q)or hybrid nonthermal distribution is studied in [42].The wave frequency depending onq(α) increases by decreasing the nonextensive parameter,q(α).The general form of the non-Maxwellian distribution function, called the Vasyliunas–Cairns distribution function, is discussed numerically in [43, 44].Kappa–Cairns distribution is discussed in [45].More highly energetic particles can be generated by this Kappa–Cairns distribution than that of both Kappa and Cairns distributions.Linear and nonlinear Alfven wave propagations in generalized (r,q)distribution were studied in [46].Tsalli’s distribution function[47–50]is applied to show the nonexistence of unstable acoustic modes in a pair-ion plasma in [51].Landau damping and instabilities of waves in Tsalli’s or nonextensive distribution were discussed in [52–56].

This paper will discuss the anisotropic thermal distributed Cairns distribution function for Langmuir waves with twisted electrostatic waves carrying OAM.In space, there is a chance for distribution to deviate from equilibrium.We apply such existing distribution functions interacting with twisted waves carrying OAM.It is important to have as many numerical results as possible for comparison with future observational data.First,we introduce shortly twisted waves in section 2 for later convenience.Section 3 discusses the dispersion relation and Landau damping for both bi-Maxwellian and Cairns distribution functions.The bi-Maxwellian distribution is an anisotropic Maxwellian one and the Cairns distribution reduces to bi-Maxwellian in a certain limit.We compare these results depending on the presence of a twisted wave.This paper finishes with a discussion and conclusions in section 4.

2.Twisted waves

This section reviews twisted waves [57, 58], which seems to be helpful for the remaining study.Even though the twisted wave of an electromagnetic field carrying OAM is generated in the laboratory, it can be generated by a black hole or gravitational wave.

The twisted Langmuir waves for the Poisson–Vlasov equation after linearization by puttingwith the conditionand neglecting higherorder terms satisfy the following equation:

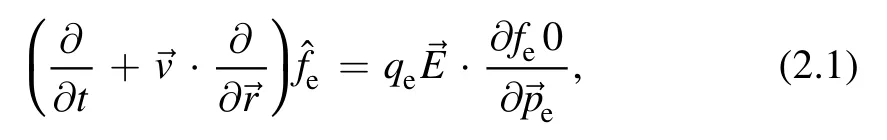
A non-planar (helical) electric field carrying OAM satisfies

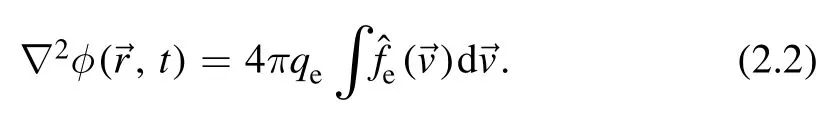
Assuming slowly varying amplitude of the twisted electrostatic wave along thez-axis with potential φ=eikz−iωt,which is a plane wave, we have

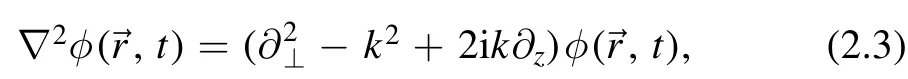
Applying paraxial approximationwhich means the gradual variation of the field along thezdirection, i.e.that the beam does not spread much from the axis or almost parallel to thez-direction, this equation reduces to

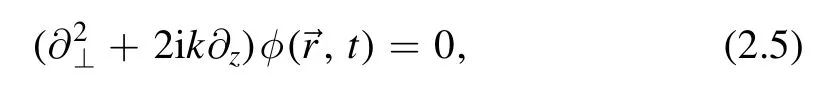
such that

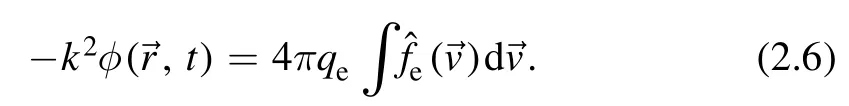
We introduce Laguerre–Gaussian(LG)modesFpl(r,z),which is a solution of paraxial equation (2.5) in cylindrical coordinates

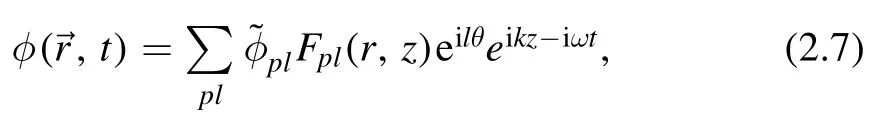
wherepandlare radial and angular mode numbers,specifies mode amplitude and θ is an azimuthal angle,respectively.The LG modeFpl(r,z) is [59]

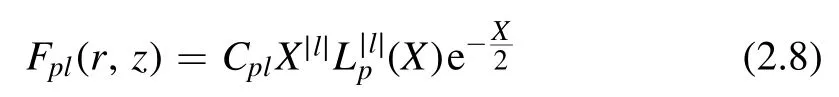
whereX=r2/w2(z) andw(z) is a beam waist.Here,pandlare integers and denote radial and angular mode numbers,respectively, and θ is an azimuthal angle.Moreover,=CplHere,Flpsatisfies the orthogonality condition

Considering the Vlasov equation with the following LG modes

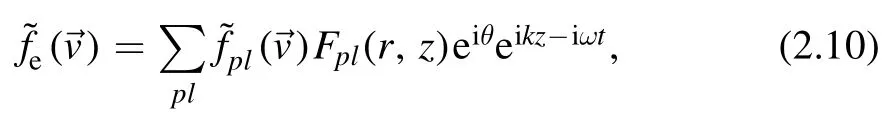
we obtain, after integration byrdr, the following equation:

withx=ω −kvz−lqθvθandy=qrvr+qzvz.We solved the Vlasov equation under paraxial approximation.Here, →

have been introduced:

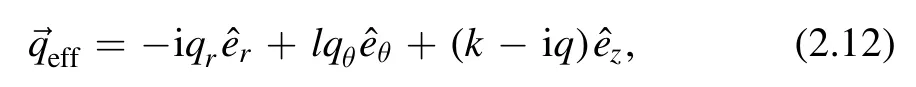
whereqjandqθare given by

The dielectric function ∊can be expressed as ∊(ω,k,lqθ)=1+χe(ω,k,lqθ), where χe(ω,k,lqθ) is a susceptibility of electrostatic waves in twisted plasma:

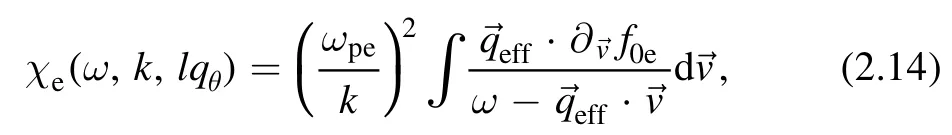
is interpreted as a new wave vector.In this integral there is a pole along the direction→.

The denominator will vanish when the following condition satisfies

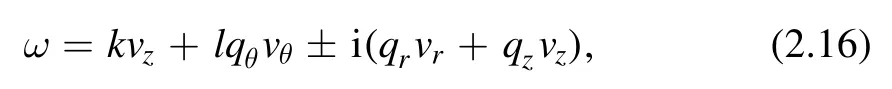
giving the resonance condition, which is quite similar to Landau resonance.Furthermore, for |qr|, |qz|≪|qθ|,y=qrvr+qzvzcan be neglected so that we have ω=kvz+lqθvθ.This means that there are two degenerate Landau resonances.We thus arrive at the following relation,which we will use for the construction of dielectric permittivity throughout the paper:

Introducing new variablesuz(vθ) anduθ(vz) given by

we get

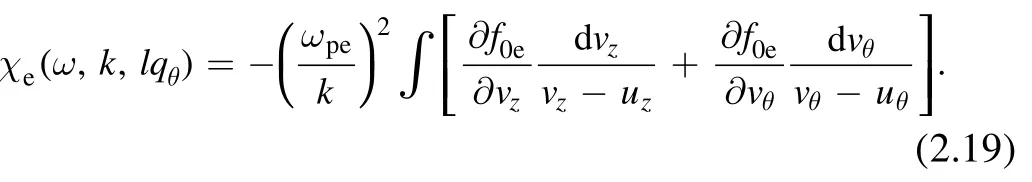
This final result is obtained based on a solution of the Vlasov equation under the assumption of paraxial approximation of equation(2.11).Note that two poles appear with respect touzanduθafter the approximation of the twisted wave.We need to explain the appearance of two poles in more detail,as was discussed in [14].The integration of the permittivity should be taken over the resonance line invzand thevθplane as the imaginary part of permittivity is the sum of two delta functions(see equation(21)and figure 1 in[14]).This means,for example, that whenlqθ→0 the resonance line becomes parallel tovθgiving ordinary Landau resonance ω=kvz.

3.Twisted Cairns distribution

This section will consider the anisotropic temperature effect of electron distributions in both bi-Maxwellian and Cairns with twisted electric waves.In nature, the distributions of plasmas have a chance to deviate from the equilibrium distribution.Our present studies for the distribution functions of both bi-Maxwellian and Cairns are only part of such nonequilibrium ones.The development of observational power surveying the space may require theoretical data as both wide and much as possible to compare with and correctly construct the theoretical model.Our work would be a part of the building block.

3.1.Bi-Maxwellian distribution

Let us first consider the bi-Maxwellian distribution function[60–62] for electrons such that

By inserting the following relations

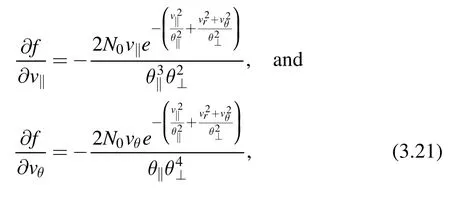
into equation (2.17), the dielectric permittivity can be obtained after the integration

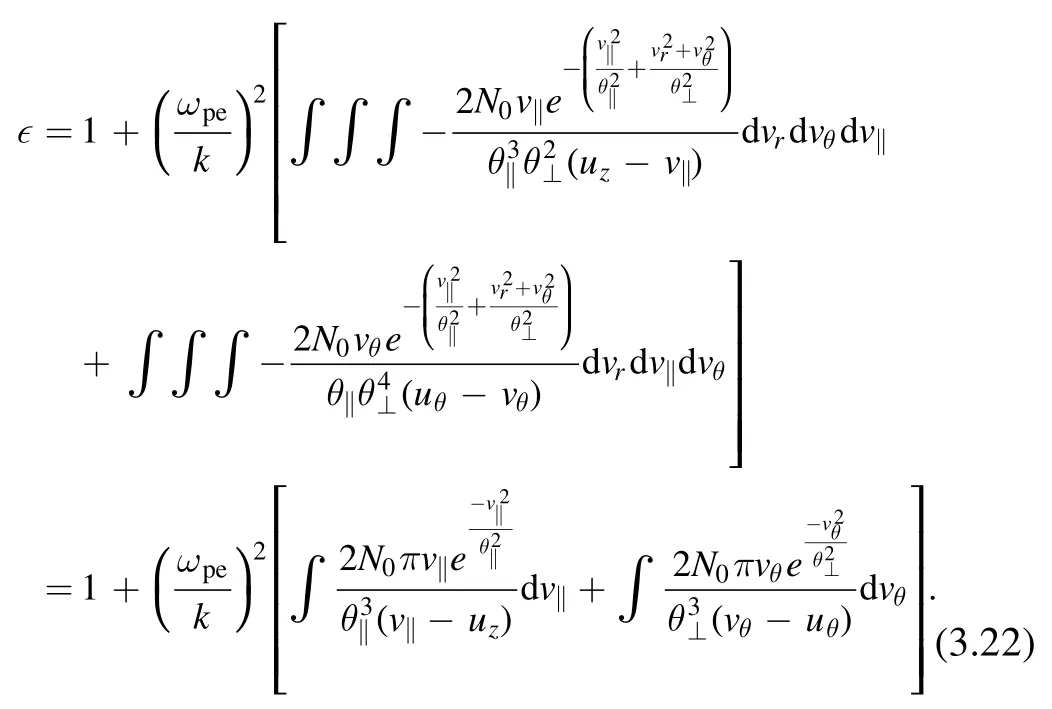
To find the dispersion relation and Landau damping,we need to consider the limituθ≫1 anduz≫1.Then, usingwe have

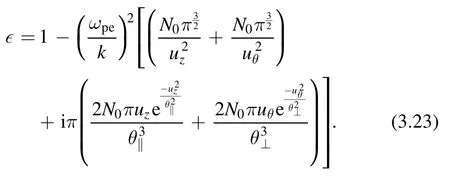
The real part of ∊gives the dispersion relation,which is given by

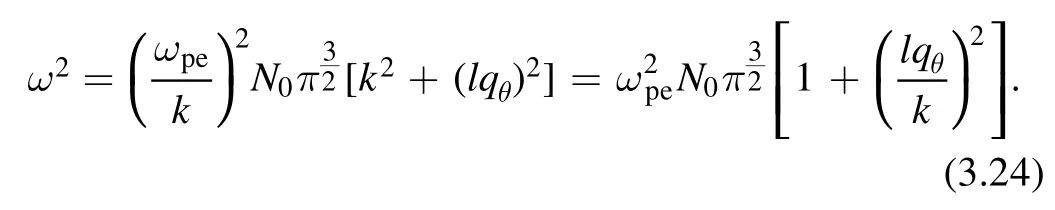
This dispersion relation reproduces the leading term of equation(24)in[57]as κ →∞.In leading order,there is no dependence on the anisotropic temperature.The effect of the twisted wave turns out to be just an addition to the conventional dispersion relation because the last term drops in the absence of twisted waves, (lqθ→0).Because ω is simply proportional tok(i.e.ω ～k), in other words, linear ink, there is no soliton in weak dispersive medium.If we start with the inclusion of a nonlinear differential equation instead of a linearized one,we would have a soliton equation, such as the KdV equation.

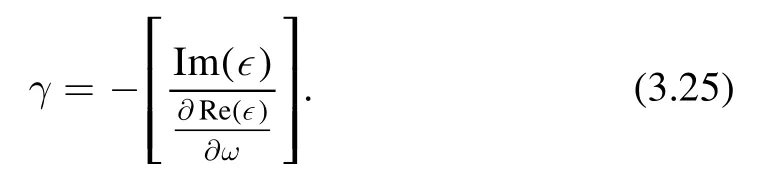
The Landau damping rate can be obtained by the relation

In the present case, after insertinguz=ω/kanduθ=ω/lqθ,we have

which leads to

where ω given in equation (3.24) is inserted.This γ is definitely negative for all real values.This represents damping leading to dissipation without a collision.If γ is positive, the rate grows and represents instability.The thermal anisotropy,θ⊥≠θ‖, can decide which term contributes to the γ dominantly.The condition θ‖<θ⊥with equal ω/kand ω/lqθwill lead to the conclusion of the dominance of the first term and vice versa.We can also check that without the twisted wave mode limit,lqθ→0, we have a result without thelqθdependence term, which is a usual result for the bi-Maxwellian distribution.Note that equations (25)–(27) in [57] as κ →∞agrees with our result in the limit Λ →0.

In figure 1, we plotted Landau damping γ for the variation ofk/lqθ.The abscissa is θ‖and the ordinate is θ⊥.Ask→0,or the twist wave is more important, there is a valley along the direction to θ‖while, ask→∞,or the twist wave is negligible,there is a valley along the direction to θ⊥.Whenk=lqθthere is a minimum in which θ‖=θ⊥.For a fixedk/lqθ, there is an anisotropic dependence of Landau damping.

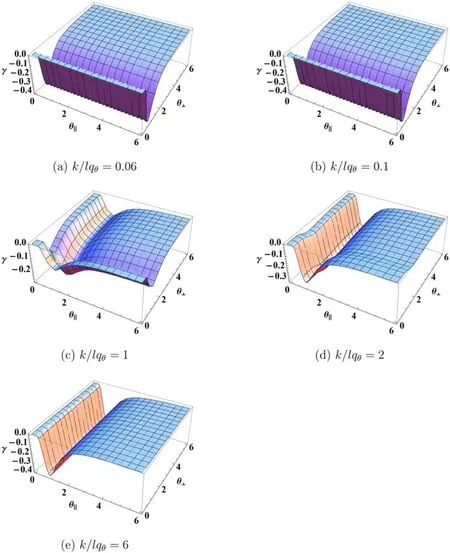
Figure 1.Landau damping γ for bi-Maxwellian distribution.

With the two (uz,uθ) independent variables, we are able to consider other different limits ofuzanduθ:

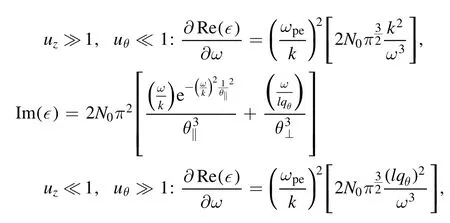
Two more conditions that determined the Landau damping showed up, which is absent without twisted mode.Here, γ becomes smaller(the absolute value of γ becomes bigger)in two different limitsuz≫1,uθ≪1 anduz≪1,uθ≫1.Except for the case ofuz≪1 anduθ≪1, which gives −∞, we can evaluate the Landau damping and we see that the absolute value of γ is reduced.It means that the damping rate increased.It can be said that twisted mode plays the role of a control parameter.The limit ofuz≪1 anduθ≪1 may give rise to a non-vanishing∂ Re(∊)∂ωwhen higher-order terms’ contributions are included, and which is out of the scope of this present work.The conditionuz≪1 anduθ≪1 is related to the ion sound wave.Thus, the extra relation may cause the mixture with the sound wave: the rangeuz≪1 might arise for the consideration of an acoustic wave (the rangeuz≪1 is often taken for the acoustic wave), so we use the term “mixture” for convenience.

A similar study appeared in [63, 64].When κ →∞, bikappa distribution reduces to the bi-Maxwellian one.

3.2.Anisotropic twisted Cairns distribution

Now, let us consider the anisotropic Cairns distribution function (bi-Cairns).The Cairns distribution, which will be considered for species α, is given by [65–71]

where α will stand for electron.In the limit of the nonthermal parameter Λ →0, this Cairns distribution function reduces to the bi-Maxwellian one.This distribution is first introduced to study solitary structures in the upper ionosphere by nonthermal electrons.It is used for the explanation of density depletion detected by the Freja satellite, where so-called cavitons are observed.The isotropic Cairns distribution has a shape similar to the Maxwellian one but has shoulders on both the left and right depending on the value of the nonthermal parameter Λ.If Λ is big,the shape has two large humps.This distribution can be observed in space plasmas, where thermodynamic inequilibrium is natural and high-energy tails are exhibited.Using the fact that the perpendicular velocitycan be rewritten aswe have rewrittenf0as

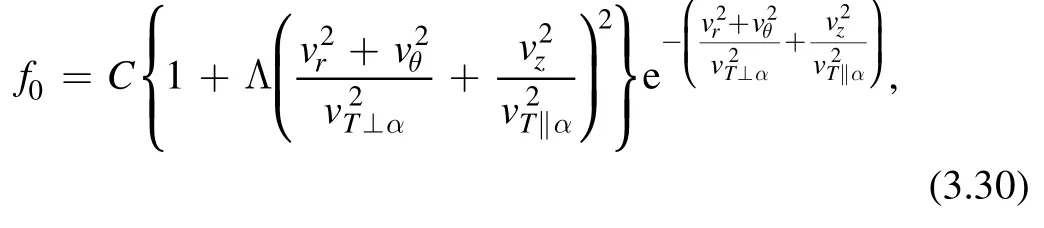
where

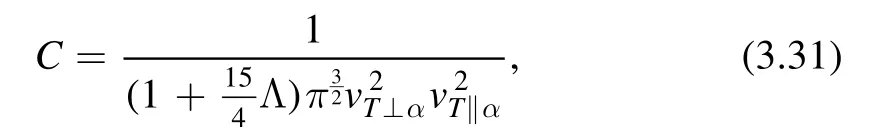
The dielectric permittivity discussed in the previous section has the form ∊=1+χ and,puttingqeffinto the χ,we finally arrive at the following form

where again

Usingf0from the Cairns distribution relation we have,after some integration, the following equation:

which can be written as

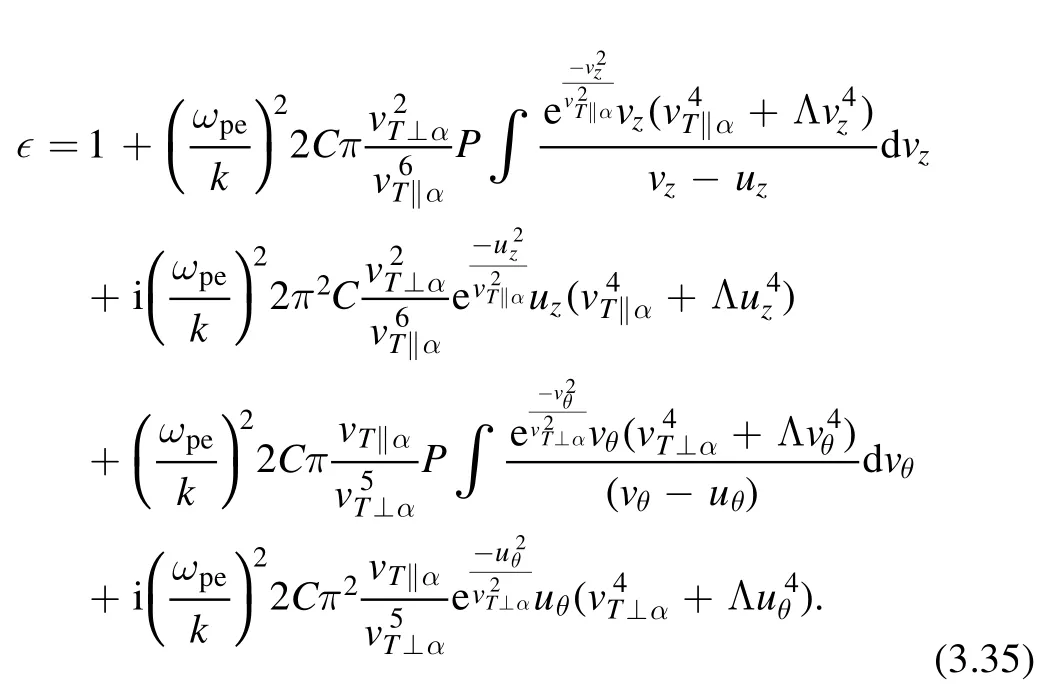
The results may depend heavily on the relative magnitude of eachvT⊥αandvT‖α:vT⊥α/vT‖α≫1 orvT⊥α/vT‖α≪1.In the first case, the first term in equation (3.34) is more important than the second one and vice versa.In the sense of distribution function, the perpendicular direction is suppressed compared to the parallel direction.

In the limituz≫1 andvθ≫1,the integration reduces to

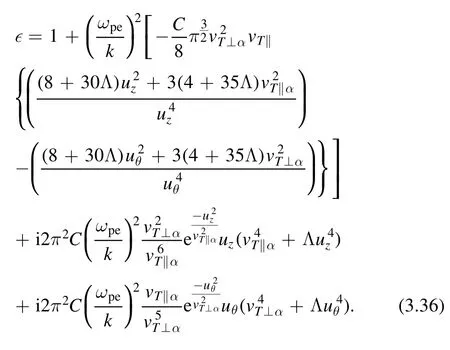
After puttinguz=ω/kanduθ=ω/lqθinto the above equation, we have

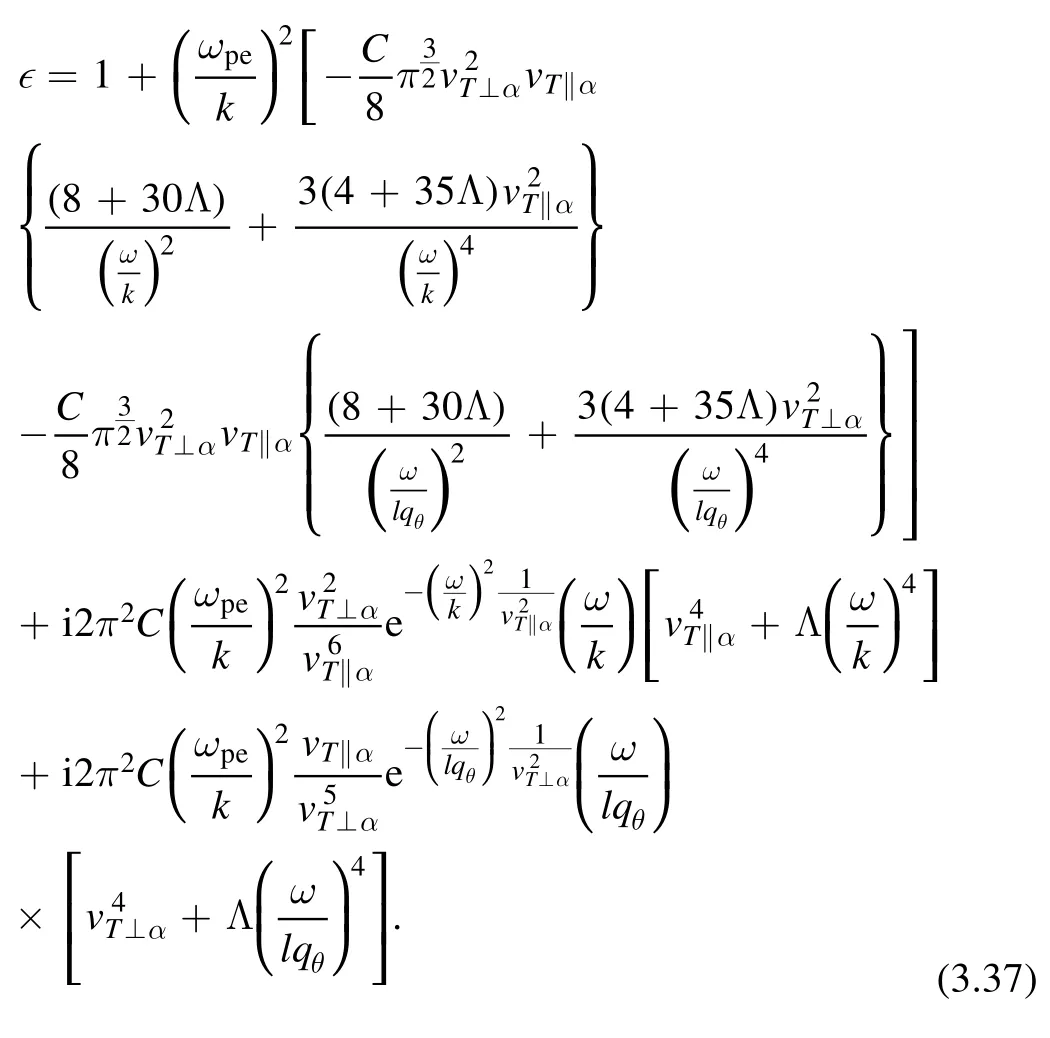
The real part of ∊=0 gives the dispersion relation:

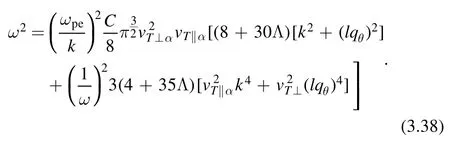
Unlesslqθis an imaginary value, there is no chance of becoming negative ω2.When we focus on a big ω, then the(1/ω)2term can be neglected.In this case,ω2is simplified and is reduced to

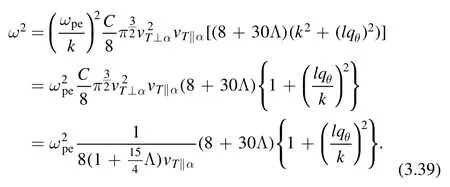
In this leading order, we see the disappearance of the perpendicular direction of anisotropic temperature dependence.It will show up in a higher order.Note also that as Λ →0 this result reduces to equation (3.24) for bi-Maxwellian distribution as it should.

In the limituz≪1 anduθ≪1,the integration reduces to

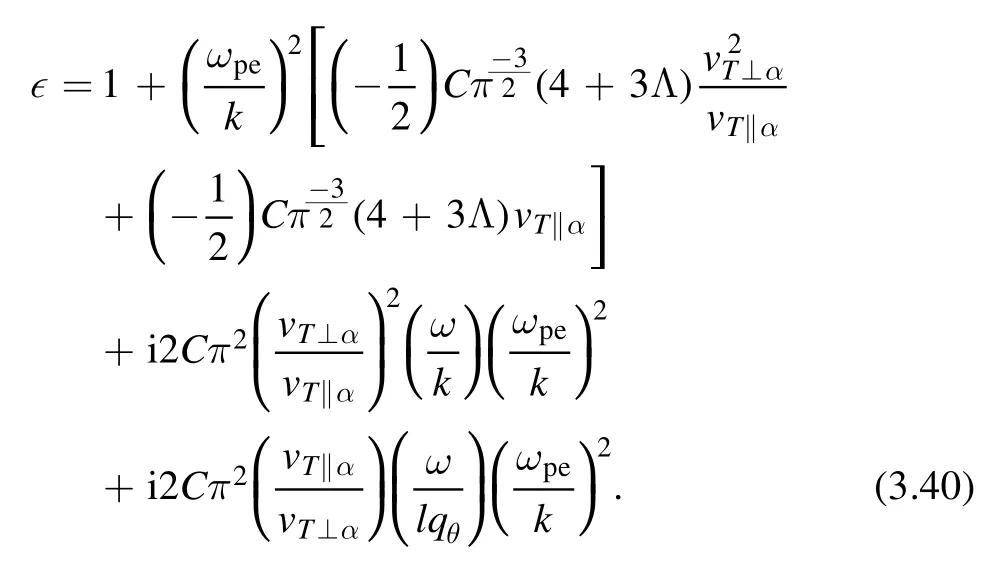
The Landau damping rate γ can be obtained by again considering the formula for the limituz≫1 anduθ≫1:

which is expressed as

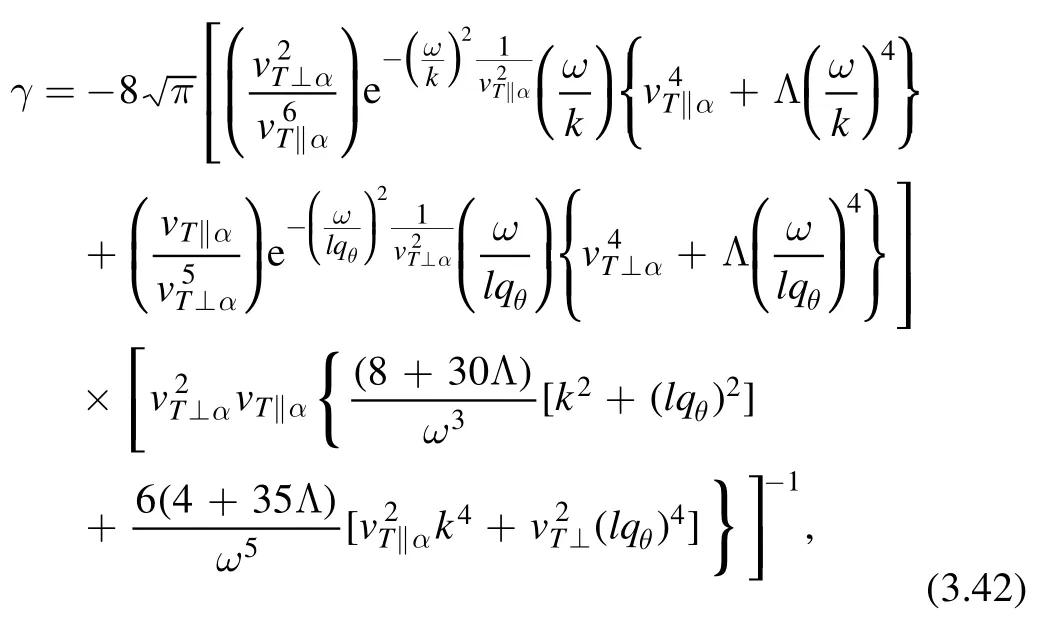
where ω is given in equation (3.38) or (3.39).When Λ →0,this relation reduces to the bi-Maxwellian result by inserting ω.When the reduced ω is inserted into γ and by keeping the higher order in ω, we get

WhenvT⊥α≫vT‖α, the first term then dominates and the contribution to the damping rate comes mainly from the first term and vice versa.Moreover, when the twisted wave dominateslqθ≫k, the first term again dominates and vice versa.When Λ=0, we get Landau damping:

which is similar to equation (3.27), and we confirm that the Landau damping of Cairns distribution leads to that of the bi-Maxwellian one in the Λ →0 limit as well.

In figure 2,we plotted the Landau damping γ depending on the variation ofk/lqθ.It is similar to figure 1 but differs in that the depth of the valley is not finite but infinite.Besides,the behavior ofk/lqθ→0 andk/lqθ→∞is not symmetric,as was seen in figure 1.Askbecomes bigger, a valley appears along the ordinate θ⊥.Atk=lqθ,a finite damping rate exists.Ask→0,or the twist wave is more important,there is a deep valley parallel to the θ‖but it vanishes near θ‖=0.The discrepancies might disappear if we take the Λ →0 limit and we have a result more similar to figure 1, i.e.the depth of the valley becomes finite.

As was discussed in the previous section, we may take different limits:

Here,ω is again given in equation(3.38).As was discussed in the positive sign of ω2for the real value oflqθ,this γ is always negative for such a reallqθ.As discussed in non-Maxwellian distribution, twisted waves also play the role of a control parameter for γ.As was seen in the bi-Maxwellian case,whenuz≪1,uθ≫1 anduz≫1,uθ≪1 the γ (|γ|) becomes smaller (bigger) than that ofuz≫1,uθ≫1.Here, again, the conditionuz,uθ≪1 is related to the consideration of an ion sound wave.The extra relation may again cause the mixture with the sound wave.

Instabilities may arise when the damping rate γ grows.This happens when γ>0.This seems impossible unlesslqθis imaginary.As a reference,there is a Gardner’s theorem insisting that a single humped velocity distribution function is stable.

4.Conclusions and discussion

In this study,we calculated the Landau damping rate for both bi-Maxwellian and Cairns distribution functions under the background of twisted electrostatic waves.These waves give more possibilities in withdrawing dispersion relations: in addition touz≫1,uθ≫1, we have two more,uz≫1,uθ≪1 anduz≪1,uθ≫1.It seems that the twisted wave plays the role of a control parameter, which determines the important contribution between the terms.We propose that the two extra limits are related to ion sound waves and lead to,say, mixture with a sound wave.It is unfortunate, however,that there is no evidence of twisted bi-Maxwellian and twisted Cairns distributed plasmas.Experimental efforts or astrophysical observation are required for the justification of our work.

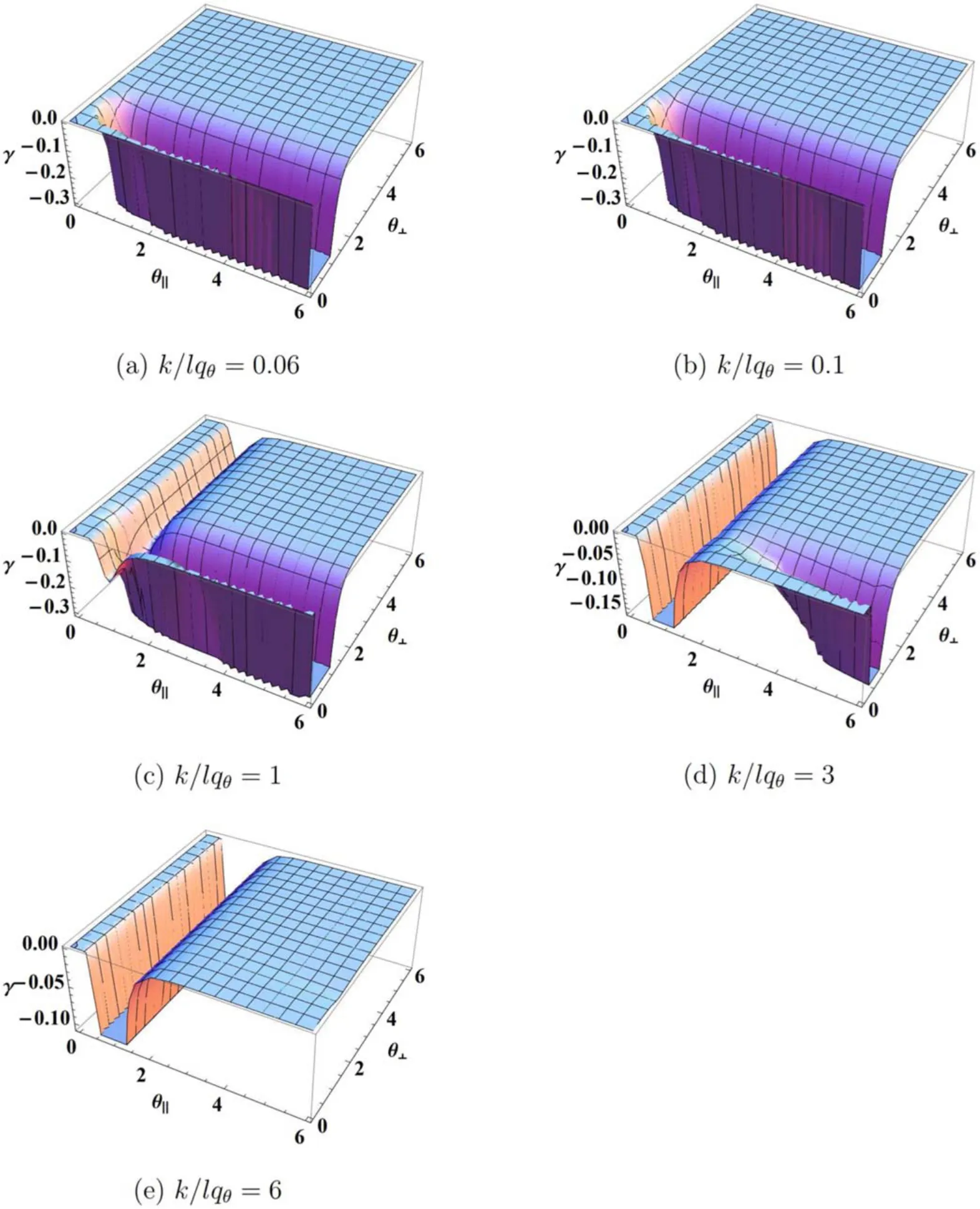
Figure 2.Landau damping γ for Cairns distribution.

Anisotropic temperature distribution leads to selection of the dominant terms in the Landau damping rate γ.Since the perpendicular direction is related to the twisted waves, the contribution from twisted waves becomes smaller as the electron kinetic energy becomes larger along the perpendicular direction.

Unfortunately, within the author’s scope, there is no convincing observational (spatial) twisted wave outside laboratory experiments.However, there are some possibilities induced by Kerr black holes and gravitational waves [35–38, 72].We hope that the existence of twisted modes in the space can be seen indirectly by comparing our obtained results with observations.For the benefit from measurement, see [33, 34].As discussed in [35–37], rotating black holes (e.g.Kerr black holes) can emit gravitational waves carrying OAM and can even twist the wavefront of the light (photon) passing nearby.We expect that this twisted spacetime may twist electrostatic waves as well.When this twisted wave interacts with nearby anisotropic bi-Maxwellian distributed or bi-Cairns distributed plasmas,it is unavoidable to consider the effect of twist waves in the kinetic theory of plasma.Then, our present study would be useful and astonishing if the observation of Landau damping in such a case agreed well with our prediction.This study can also be used in the search for unidentified particles after observation of events that have occurred as a result of a rotating black hole generating twisted waves.For neutral particles, a similar phenomenon can occur when the twisted gravitational wave [38, 72] passes the region of particles.

Our presentation with twisted waves can be extended to many distributions: almost all known distributions, such as kappa extended distributions.Moreover,it can be extended to plasmas such as ion-acoustic and dust ion-acoustic plasmas.It would also be interesting to study magnetized Landau damping with twisted waves.Our paper is limited to only collisionless plasma and it could be extendable to the case with collisions.

Almost all calculations can be carried out using wellknown software,e.g.Mathematica.It would be very useful if there was a computer program that could calculate permittivity, dispersion and Landau damping from one touch of a keyboard for any given distribution functions.Unfortunately,however, this is beyond the authors’ scope.

Finally, we would like to mention that we have ignored the mode coupling in the present work,which is indispensable for the non-zero ratio of Debye length and beam radius[73, 74].Even though the smallness of mode coupling is implied by the paraxial approximation, it affects the dispersion relation and damping rate.Hence, it would be good to calculate Landau damping with the contribution of mode coupling within the context of present distribution functions.Moreover, we have not been cautious in treating the poles in the presence of the Landau resonance line.There is a limitation, and we should have integrated along the resonance line only.Taking the limitk≪1,k≫1,lqθ≪1,lqθ≫1 might change the slope of the Landau resonance line in thevz,vθplane (see [14] for more detail).These are worthy of future study.

Acknowledgments

This work was supported by the Korea Institute of Energy Technology Evaluation and Planning (KETEP) and the Ministry of Trade, Industry & Energy (MOTIE) of the Republic of Korea (No.20183010032380).