用于残余振动抑制的深度神经网络输入整形器
张铁 康中强 邹焱飚 廖才磊
(华南理工大学 机械与汽车工程学院,广东 广州 510640)
多轴伺服系统如6轴工业机器人、数控车床等在自动化生产中被广泛应用,这些设备的末端执行器往往要求高速高精度到达定位点,以便快速开始下一个加工周期。由于多轴伺服系统关节及末端执行器存在固有的柔性,执行器在急停后会产生较大的残余振动,增加了等待时间;如果在加工规划过程中不考虑残余振动等待时间,则会降低定位精度,如果考虑等待时间,又会严重增加自动化加工中辅助行程的时长。
输入整形器作为一种前馈控制方法可以用来有效地抑制残余振动。在已知系统的固有频率及阻尼比的前提下,理想的零振动(ZV)输入整形器可以完全抑制残余振动,但是此方法要求准确地获得系统模态参数,在系统参数存在误差的情况下,往往抑振效果不佳。
为提高ZV整形器的鲁棒性,Singer等[1]提出在ZV整形器中加入一阶微分约束,得到零振动微分型(ZVD)整形器。Singhose等[2]在此基础上提出通过增加脉冲数量及设定一定残余振动允许量来提高整形器的鲁棒性,如多脉冲超不敏感输入整形器。增加脉冲数量的代价是使得整形后的轨迹时滞时间增长,因此Vaughan等[3]在输入整形器中引入负脉冲设计方法,缩短了脉冲序列长度,进而缩短了整形后轨迹的时滞时间。对于复杂的柔性串联机构,不同位姿对应的模态参数的区别可能会较大,单纯用固定的输入整形器无法保证在不同轨迹下都有良好的抑振效果。
因此研究者将自适应算法引入到输入整形器设计中,自适应输入整形器分为两类:间接自适应与直接自适应输入整形器。
间接自适应输入整形器针对不同轨迹下模态参数的变化重新进行时域或者频域的辨识[4],进而设计新的输入整形器。Tzes和Khorrami等[5- 6]针对振动模态与载荷关系的估计,提出时变传递函数估计(TTFE)和经验传递函数估计(ETEE)系统参数辨识算法。该方法需多次对振动信号进行快速傅里叶变换(FFT),计算量繁重。Kojima等[7]通过实验数据分析得到连杆角度与振动频率近似四阶函数关系,对函数系数进行近似计算,从而实现根据连杆角度估算系统振动频率,此方法仅限于单轴或两轴机构,对于多轴系统用四阶函数进行拟合的方法不再适用。Fasih等[8]根据塔式起重机缆索长度和有效载荷与系统模态参数的实验数据,建立人工神经网络学习二者间的非线性模型,通过神经网络模型得到缆索和载荷变化后的模态参数,由于依旧采用ZVD输入整形器,导致无法应用在复杂多模态系统。Chang等[9]为简化残余振动信号采集过程及FFT带来的复杂计算过程,提出基于动力学模型计算系统不同构型下整形器时滞时间的自适应算法以及对有效载荷的自适应方程,但动力学模型的建模与模型参数辨识误差会限制自适应算法的效果。
直接自适应输入整形器从残余振动信号入手,避开复杂的系统辨识过程,以减少参数辨识不确定性对输入整形器抑振效果的影响。在最优任意时滞滤波器(OATF)[10]基础上,Rhim等[11]针对单模态系统,对残余振动信号应用递归最小二乘法(RLS)优化计算输入整形器的系数。在此基础上,Rhim等[12]将该方法拓展到多模态,根据系统实际模态数选择整形器脉冲数,适用性广且抑振效果较好。Chu等[13]在递归最小二乘过程中加入了恒定的遗忘因子,在迭代过程增加最近时刻观测数据在代价函数中的比重,提升了整形器的跟踪性能,但在只能获知系统少量先验知识的情况下,很难计算最优的遗忘因子。
本研究首先提出了一种自适应遗忘因子更新算法,从输入整形器均方误差函数对遗忘因子的标量梯度出发,应用自适应算法在环境参数不确定的情况下调整遗忘因子以提升抑振效果;并将该算法嵌入到无遗忘因子递归最小二乘法(RLS)迭代过程中,得到带自适应遗忘因子的后置输入整形器。再在自行搭建的多轴伺服平台验证该算法,并与RLS后置输入整形器进行对比。之后针对带自适应遗忘因子的后置输入整形器(AFFRLS)在应用中每次重新规划轨迹后需重新优化输入整形器系数向量的问题,引入多层全连接神经网络模型,将残余振动信号作为网络的输入层,整形器系数向量作为输出层,应用多组激励轨迹训练网络,最终将训练得到的神经网络模型应用在多条新的圆弧轨迹中验证基于神经网络模型的输入整形器抑振效果,并与RLS后置输入整形器进行对比。
1 后置自适应输入整形器
后置输入整形器是一种从柔性系统输出入手的反馈控制方法,其原理是应用自适应算法对柔性系统的输出进行优化,得到当前最优的输入整形器,再将得到的最优整形器反馈至预整形端,最终实现对期望轨迹r(t)的整形及系统残余振动的抑制,其中t为时间。其控制流程图如图1所示。
图1中,x(t)和y(t)分别为柔性系统的输入和输出,yd(t)为经理想输入整形后的期望输出,yf(t)为当前输入整形器的估计输出,e(t)为整形器期望输出与实际输出之间的误差。

图1 后置输入整形器流程图Fig.1 Flow chart of post input shaper
1.1 后置自适应输入整形器的设计
后置自适应输入整形器形式上为有限脉冲响应滤波器(FIR),它建立在最优任意时滞滤波器的基础上,任意时滞输入整形器[10]的一般形式为
(1)
式中:wj为输入整形器中第j个脉冲的系数;δ(t)为单位脉冲函数;td是整形器任意时滞时间,对于输入整形器来说,不同的td对应不同的脉冲系数wj(j=0,1,…,k),td在确定后一旦改变,会导致wj跟随改变才能保证滤波器良好的抑振效果,k+1为输入整形器的脉冲数。整形后的系统输入x(t)为期望输入r(t)与任意时滞输入整形器的卷积,
x(t)=r(t)*f(t)
(2)
由式(1)写出任意时滞输入整形器的离散形式:
F(z)=w0+w1z-Δ+w2z-2Δ+…+wkz-kΔ
(3)
其中:Δ=td/ts(Δ为整数),ts为控制系统的最小采样时间;z-1为离散时间信号上的单位延时算子;输入信号r(t)与z-Δ做运算,其结果为r(t-Δ)。可以用横向滤波器结构来表示式(2),如图2所示。
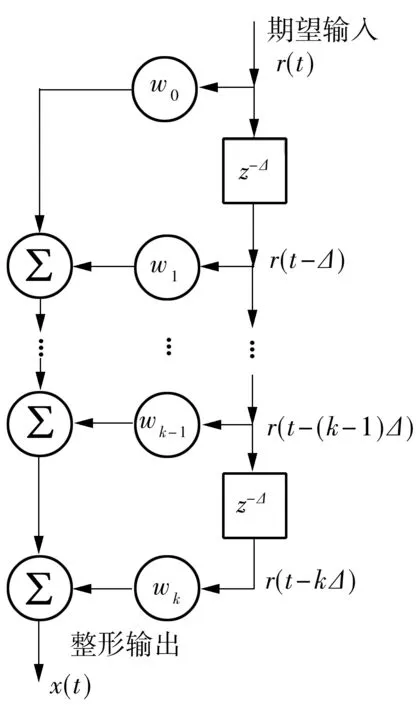
图2 任意时滞输入整形器的横向结构
1.2 后置自适应更新算法
基于柔性系统的输出响应y(t),定义Ψ(i)为i时刻的抽头输入向量,
Ψ(i)=[y(i)y(i-Δ) …y(i-kΔ)]T
(4)
定义w(n)为n时刻输入整形器的脉冲系数向量,
w(n)=[w0(n)w1(n) …wk(n)]T
(5)
n(n=1,2,…,h)时刻整形器系数向量w(n)对应的系统估计输出为
yfn(i)=wT(n)Ψ(i),i=1,2,…,h
(6)
由系统经理想整形器的输出为yd(i)可知,对应时刻i的估计误差为
en(i)=yd(i)-yfn(i)
(7)
在后置输入整形器每次更新过程中,为实现系统输出零残余振动,需要建立代价函数如下:
(8)
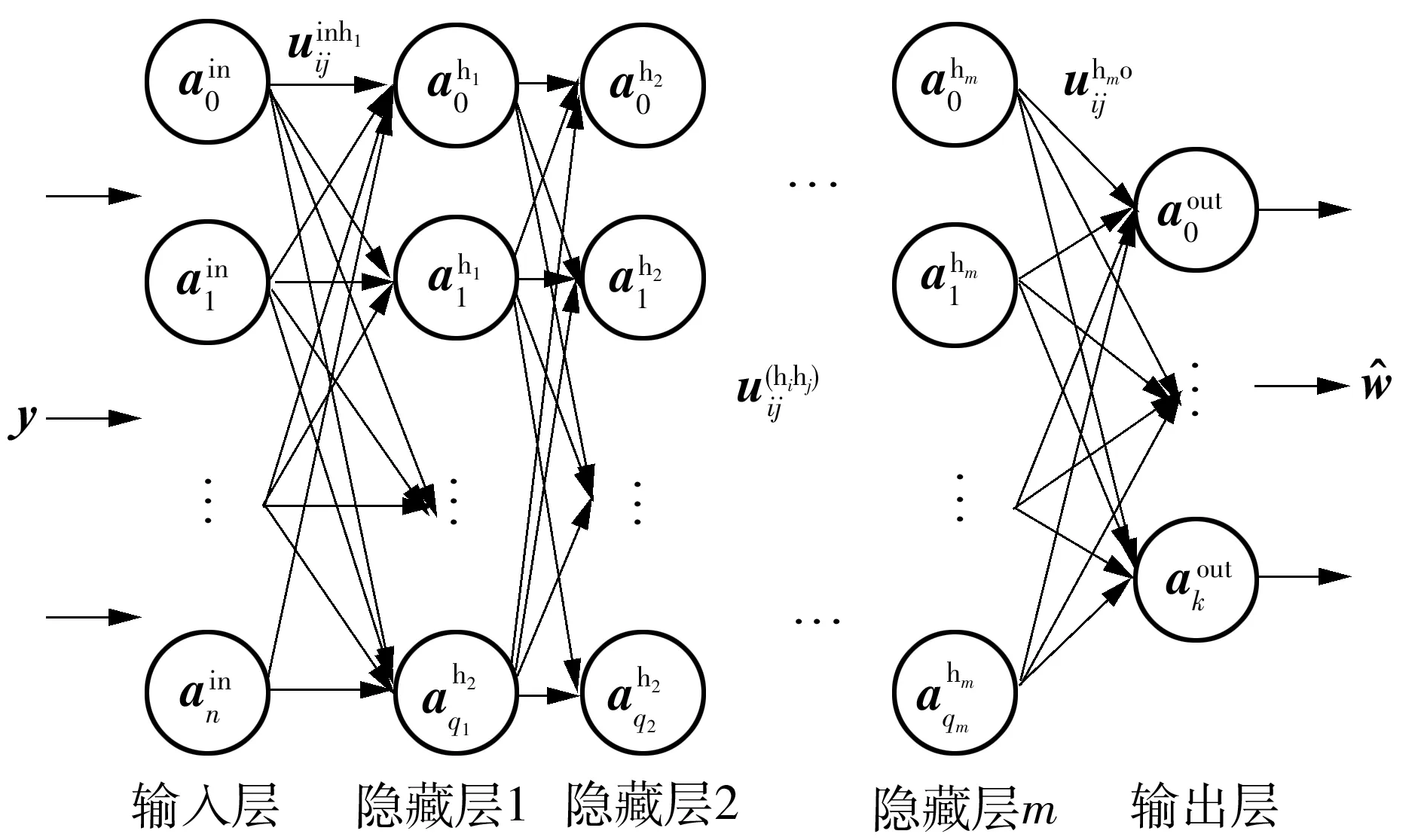
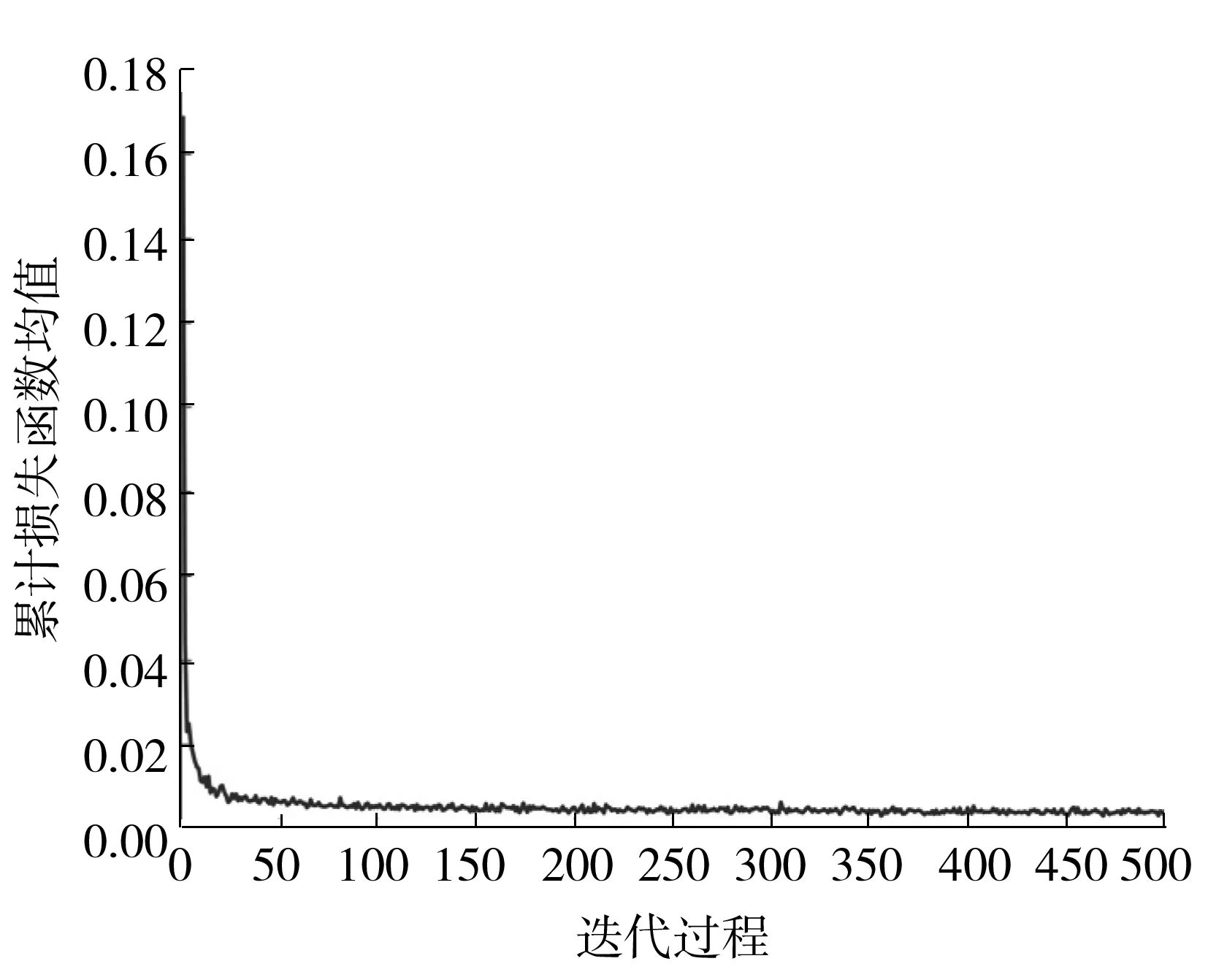
其中h为系统完全停止振动的离散时间点数。C(n)为n时刻下在系数向量为w(n)的输入整形器作用下从i=0到i=h系统输出的误差平方和。进一步,优化算法的目标应在C(1),C(2),…,C(h)中取得极小值。由于理想的零残余振动整形器在系统停止工作的kΔ时间后,系统的残余振动应为零振动,也即当i>kΔ时,yd(i)=0,如图3中零残余振动(ZRV)输入整形器所示;而当0 (9) 式(9)强调代价函数针对残余振动信号进行定义,为方便表达,在后文中应用式(8)进行推导。自适应算法以递归最小二乘法(RLS)为基础,引入加权因子ρn(i): (10) (11) 由于遗忘因子小于1,ρn(i)对于越早的误差样本,在代价函数中赋予越小的权重,使得优化过程中更加注重最近观测的数据样本,而遗忘时间过早的样本在代价函数中的影响。这使得后置自适应输入整形器具有一定的跟踪能力。 图3 ZRV 3脉冲输入整形器的理想输出响应示意图 为进一步在后置输入整形器中引入基于RLS的自适应更新算法,将式(11)改写成矩阵形式: C(n)=eT(n)Λ(h)e(n) (12) 其中,eT(n)=[en(1)en(2) …en(h)]T,Λ(h)则是由加权因子构成的对角矩阵: (13) 再将抽头输入向量写成矩阵形式: X(h)=[Ψ(1)Ψ(2) …Ψ(h)] (14) 对于时刻n系数向量为w(n)的整形器,从时刻i到h整形器的输出矩阵为 y(h)=[yfn(1)yfn(2) …yfn(h)]T (15) 相应的理想输出矩阵为 yd(h)=[yd(1)yd(2) …yd(h)]T (16) 由式(6)、(14)、(15)得到整形器估计输出矩阵: y(h)=XT(h)w(n) (17) 再由式(7)、(16)、(17)可以写出估计误差矩阵: e(h)=yd(h)-y(h) (18) 因此将式(17)、(18)带入式(12)中可得到 (19) 其中: z(h)=X(h)Λ(h)yd(h) (20) (21) (22) (23) (24) (25) (26) 其中向量k(h)称作增益向量,其表达式为 (27) (28) 对于式(28)中的n,在式(6)、(17)中强调n时刻的整形器参数对i从1到h抽头输入向量的滤波响应,而在式(28)中,n强调递推过程中的迭代,且在迭代过程与h同步,同样取值为1到h,因此可用式中h替代n: (29) (30) 称为先验估计误差。由式(29)、(30)可知,整形器系数向量的更新依赖于上一时刻的参数向量估计及先验估计误差。另外,期望轨迹经输入整形器整形后,应保证轨迹的幅值不发生改变,因此在RLS算法中添加归一化约束条件: gTw(h)=1 (31) 遗忘因子修正的依据为RLS算法中的均方误差: (32) (33) (34) (35) 将式(30)、(34)带入式(33)可将标量梯度重新改写为 ΨT(n)W(n-1)e(n)] (36) 再将式(35)与式(29)带入到式(34),可以得到W(n)的更新式: W(n)=[I-k(n)ΨT(n)]W(n-1)+ S(n)Ψ(n)e(n) (37) (38) 实际应用中,标量梯度用瞬时估计值来替代式(36)中统计意义上均值的计算: (39) (40) 为进一步提升算法效率及稳定性,在式(40)中再加入约束: (41) 综合以上式(37)、(38)、(40)、(41)以及标准的RLS算法即得到带有自适应遗忘因子的RLS算法如下所示。 算法:带自适应遗忘因子的后置输入整形器 输入:初始化系统模态数N,时滞时间td,采样长度length. 生成抽头输入向量Ψ: forifrom 1 to length Ψ(i)=acc(i)(函数acc()来自式(4)) end 初始化增益向量k(0)并更新: forifrom 1 to length 更新整形器系数向量: 更新遗忘因子 : W(i)=[I-k(i)ΨT(i)]W(i-1)+S(i)Ψ(i)e(i) end 输出: a(i-Δ) …a(i-kΔ)]T,其中a为加速度传感器采集到的残余振动信号。 在应用带自适应遗忘因子RLS算法优化输入整形器过程中,存在着每次迭代优化计算时间较长的问题,在期望轨迹频繁变化的应用场景,降低了实际效率,因此引入多层全连接神经网络模型来学习优化输入整形器系数向量这一非线性过程。 多层神经网络又称多层感知机(MLP),主要由大量简单的神经元组成,网络结构包括:输入层、隐藏层、输出层。其中在多层神经网络模型中通常隐藏层大于一层,以提高网络的拟合能力。多层神经网络首先通过前向传播训练集产生输出,再基于网络的输出计算误差,进一步反向传播误差,并通过误差对各层神经元的权值系数求导更新网络模型[17]。理论上多层神经网络可以拟合任意的非线性映射关系。为缩短多条任意期望轨迹每次迭代优化整形器系数向量的时间,将任意轨迹的残余振动信号作为网络模型的输入层,将整形器系数向量作为输出层建立多层全连接神经网络,如图4所示。 图4 多层全连接神经网络模型Fig.4 Full connection multilayer perceptron model 图5 网络层间运算过程示意图 为进一步避免过拟合现象,提高神经网络的泛化性能,在网络中引入随机失活正则化(Dropout)方法。在神经网络训练过程中,按照一定概率选择暂时丢弃神经元,以减少各神经元之间的过度依赖性,进而提升网络的预测准确度。Dropout方法设置在各层间,经测试,概率选择为0.3,在每次训练迭代中,训练的都是不同的子网络,最终按照权值比例推断规则,以非标准化的概率分布为基础,计算出各自网络集成后的输出。Dropout方法如图6所示。 图6 Dropout方法示意图Fig.6 Schematic diagram of Dropout method 本研究选择在自主搭建的多轴伺服运动平台上验证算法的有效性。首先选取不带遗忘因子的标准RLS算法与本研究提出的带自适应遗忘因子的(AFFRLS)算法进行对比;其次运行多段多轴伺服系统的激励轨迹[18],采集残余振动信号,应用AFFRLS算法计算最优输入整形器系数,并将多组数据作为后续多层神经网络模型的训练集,再应用pytorch深度学习框架对网络进行建模及训练,最后用新轨迹对应的残余振动信号验证神经网络模型的泛化性能。 采用自主搭建的多轴伺服运动平台模拟工业中常见的多轴运动系统如机械臂、数控车床等。控制系统选择基于EtherCAT现场总线的实时系统,实验平台及控制系统框图如图7和图8所示。 图7 多轴伺服驱动平台Fig.7 Multi-axis servo drive platform 在运动平台工作台上安装一块钢制薄板(见图7),作为放大系统柔性的单元,以便更加清晰地验证算法的有效性。倍福模块作为从站实时采集加速度传感器的电压信号,通过总线实时传输至上位机并换算成加速度信号来表示残余振动。 实验首先验证带自适应遗忘因子后置输入整形器的抑振效果,选择一条常见的四分之一圆弧轨迹进行对比实验,如图9所示。图9中上方图示出了AFFRLS算法与RLS算法相比于未整形的残余振动效果,两种后置自适应输入整形器对于残余振动均有较好的抑制作用;下方图放大了AFFRLS算法相比于RLS的抑振效果,选择残余振动振幅绝对值大小来量化抑振效果。计算可知,AFFRLS算法整形后的残余振幅相比RLS算法平均下降了28.3%,残余振幅最大下降了36.9%。因激励轨迹的设计以系统动力学模型作为约束,轨迹中包含尽可能多的运动状态,所以实验首先选择100组多轴伺服平台激励轨迹,分别采集运行停止后的残余振动信号,并按照AFFRLS算法对100组数据进行批量处理,将每条轨迹的残余振动信号及AFFRLS优化结果放入多层神经网络模型中进行训练,训练过程中的损失函数收敛性见图10。其中训练过程迭代次数为10 000次,由于迭代到中期收敛速度减慢,因此为便于观察,每隔20次取一个数据点绘图。 图9 AFFRLS后置输入整形器与RLS输入整形器抑振效果对比 图10 神经网络模型训练过程损失函数收敛过程 多层网络经过反复前向传播与反向传播后收敛,获得该实验平台对应的神经网络模型,将未在训练集中的圆弧轨迹产生的残余振动信号输入到模型中,计算得到整形器系数向量。最后应用该整形器对轨迹整形,进而验证训练得到的多层神经网络模型的有效性。因在神经网络的计算过程中,每个神经元是对数据进行简单的计算,相比AFFRLS算法节省了大量的迭代计算。在训练得到神经网络后,统计MLP和AFFRLS分别计算整形器系数向量所耗费的运算时间,在同一台计算设备上运行10次,见表1。MLP平均计算时间为0.005 4 s,AFFRLS平均计算时间为43.080 1 s。 表1 MLP与AFFRLS计算整形器系数时间 将由网络模型计算得到的输入整形器抑振效果与经RLS算法优化得到的输入整形器进行对比,基于MLP的后置输入整形器整形后的残余振幅相比RLS平均下降了21.6%,残余振幅最大下降了29.8%。如图11所示。 图11 MLP计算得到的输入整形器抑振效果与RLS后置输入整形器抑振效果对比 进一步,由图9和图11中未整形的残余振动信号可知,当振幅小于一定值可视为振动停止。为清晰对比,定义加速度信号振幅小于Acon(Acon=3 m/s2)为残余振动收敛,相应地,3种算法残余振动波峰振幅首次小于Acon的时刻称为收敛时间tcon。实验结果表明:未整形残余振动、RLS、AFFRLS、MLP整形后的残余振动收敛时间tcon分别为3 640、2 397、1 716、1 830 ms。进一步可知,AFFRLS输入整形器与基于MLP的后置输入整形器整形后的残余振动收敛时间较RLS分别缩短了28.4%,23.7%,其中MLP较AFFRLS残余振动收敛时间只增加了6.6%。随着训练样本的增多,MLP输入整形器的抑振效果会更加明显。 针对工业中多轴运动系统在急停段产生的残余振动,提出了一种带自适应遗忘因子的后置输入整形器算法,在递归最小二乘算法的基础上引入遗忘因子来提升算法在非平稳环境下的跟踪性能,并进一步根据RLS中均方误差对遗忘因子的梯度,推导出遗忘因子的迭代更新算法,最后将自适应遗忘因子算法嵌入到RLS算法中。实验证明,AFFRLS优化得到的输入整形器整形后残余振动幅值相比RLS算法平均减小了28.3%,残余振幅最大减小36.9%。 提出的AFFRLS算法在轨迹频繁变更的工况下,每条轨迹需要重新迭代优化得到新的输入整形器,这会导致算法耗时较长,应用效率降低。为解决多次重复优化带来的计算时间过长的问题,提出应用多层全连接神经网络学习残余振动到输入整形器系数的非线性关系。应用多组AFFRLS算法优化的结果训练神经网络模型,最后验证基于MLP后置输入整形器整形后的残余振动振幅,发现其相比RLS算法平均减小了21.6%,残余振幅最大减小了29.8%。并且每次计算输入整形器系数耗费时间显著缩短。

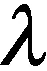
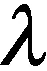



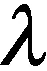
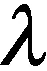




1.3 自适应遗忘因子更新算法




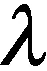

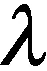
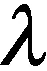


2 多层全连接神经网络模型




3 基于多层神经网络的后置输入整形器实验




4 结语

