用连分数定义莫尔条纹“准周期”

叶政君，祝怡然，黄泽江，夏成杰

(华东师范大学 物理与电子科学学院，上海 200241)

莫尔条纹是两组周期相近的条纹叠加形成的“周期”结构[1]．如图1(a)所示，两组黑白条纹平行、重叠放置，可观察到具有更长周期的莫尔条纹．这一放大周期的特性使莫尔条纹现象具有广泛的应用，如对角度、位移、材料应变的精密测量，放大晶格缺陷实现纳米探伤，纸币防伪等[2-5]．同时，近年在凝聚态物理领域发现了与莫尔条纹现象直接相关的石墨烯“魔角”特性——通过材料的层间晶格差异或者转角形成莫尔超晶格结构，引入额外的大周期势场，产生新型能带调制，在某些情况下与高温超导现象类似[6, 7]．

莫尔条纹周期长度的计算是理解并应用这一现象的基础．在大多数相关文献中，常用遮光原理求解莫尔条纹的周期[8]．我们指出，这一方法虽然在大多数情况下都能给出正确的结论，但会与某些特殊条件下的观察结果不符：例如，当两组条纹的各自的周期长度之比，接近一对相差2的互质正整数之比的情况，如5/7等；并且，其推导过程先验地暗含了“莫尔条纹的周期性是严格的”这一假设，而实际上更应该被视为一项近似，在逻辑和数学上需要更为严谨的讨论．针对这些问题，本文通过对两组条纹的周期之比进行连分数展开，严格推导了它们所形成的莫尔条纹的周期的表达式，为莫尔条纹的周期性给出了严谨的数学定义和新的理解．据我们所知，这是第一次建立起莫尔条纹现象与连分数这一基础数学形式之间的联系．

1 莫尔条纹周期计算方法的谬误

图1中的莫尔条纹由周期分别为TA和TB的两组平行条纹A、B叠加而成，不失一般性，设TA>TB，且它们的第0根线条重合．由于两组条纹周期不同，重合线条右侧的线条逐渐错开，遮光(黑色)区域的面积逐渐增加；继续向右，条纹A的第n根线条距离条纹B的第n+1根线条的间距，开始比两组条纹各自第n根线条的间距更近，即遮光面积又逐渐减少；直至条纹A的第nA根线条与条纹B的第nB=nA+1根线条几乎重合．这就形成了一套“亮-暗-亮”交错的图案，其中两组条纹的线条几乎重合之处为莫尔条纹中的亮纹，两组条纹的线条最不重合之处为暗纹．通常，人们基于上述遮光原理推导莫尔条纹的周期长度

TM=nATA=nBTB

(1)

其中

nB=nA+1

(2)

这表示两组条纹各自经过nA和nA+1个周期后再次重合．联立式(1)、(2)可解得

(3)

对于绝大多数的周期TA、TB组合，式(3)都可给出正确的结果，但也存在例外．例如，我们在图1(c)中展示利用Adobe Illustrator(Ai)软件绘制的两组周期之比为TB/TA=0.714的重叠平行条纹，直接观察图1(c)可知，这组莫尔条纹的周期约为TM=5TA，而根据式(3)计算所得的周期是TM=2.4965TA；约为计算结果的1/2．可见，对于某些TA和TB的组合，基于式(3)计算所得的莫尔条纹周期与实际观察结果不符．

这一错误本质上是由于上述推导过程中存在一系列不严谨的近似和假设，一些明显的数学漏洞被忽视了．首先，从数学角度而言，当且仅当α=TB/TA为有理数时，式(1)存在整数解nA=A，nB=B，其中正整数A、B是表示成既约分数(即最简分数)的α=A/B的分子和分母．所以，对于任意两个周期TA，TB，关于nA，nB的方程式(1)不一定存在正整数解；甚至，由于有理数在实数轴上测度为0，严格来说，两组条纹周期之比α为有理数的概率为0．更进一步，即便在某些式(1)存在整数解的特殊情况下，直接由式(1)计算出的莫尔条纹周期也可能不正确．譬如，当TB/TA=0.901=901/1000时，式(1)的正整数解所对应的莫尔条纹周期为901TA=1000TB，显然不符合观察结果(图1(b))．所以，式(1)只能是近似成立．但是，这一近似的程度，以及做此近似的合理性均未得到充分说明．第二，式(2)也隐含着人为的假设：两组条纹刚好“错开”一条时，对应于莫尔条纹的一个周期．这一假设一方面限制了能使式(1)成立的α必须具有A/(A+1)的形式，同时其本身的合理性与必要性也尚待讨论．

2 莫尔条纹“准周期”的定义

上述分析表明，周期分别为TA和TB的两组条纹各自经过nA和nB个周期后通常只能是近似重合．所以，莫尔条纹并非是严格的周期结构，将其周期称为“准周期”更为合理．

由莫尔条纹遮光原理的图像可知，计算莫尔条纹的周期长度，本质上是在寻找一组不太大的正整数nA和nB，使

|nATA-nBTB|=TA|nA-αnB|

(4)

足够小．其中，|nATA-nBTB|为两组条纹各自经过nA和nB个周期后的间距．在本节，我们为“不太大”和“足够小”这两个近似建立严格的数学定义．其他计算莫尔条纹周期的方法本质上都未加说明地采取了同样的近似[9]．所以，如何在数学上明确这一近似的含义，并找到一组符合实际观察结果的nA和nB，是一个普遍存在的问题．

图1 两组周期分别为TA和TB的平行条纹形成的莫尔条纹

2.1 有理数逼近

由式(4)可知，计算莫尔条纹的周期本质上是在寻找α=TB/TA的有理数逼近，即用一个有理数nA/nB来近似α，从而使|nA-αnB|足够接近于零．这种对数字精度的取舍存在于所有实际问题中．最为通用的逼近方法是“四舍五入”，例如将图1(b)中的0.901=901/1000近似为0.9=9/10后便可得到符合观察结果的莫尔条纹周期TM=9TA．但是，对于莫尔条纹，“四舍五入”有时并非最佳的有理逼近方式．例如，若TA=1，TB=0.931，小数α=TB/TA=0.931四舍五入近似为0.9=9/10，得到nA=9，nB=10．代入式(4)可知两组条纹各经过nA和nB个周期后的距离相差|nATA-nBTB|=0.31．对比之下，如果用nA/nB=13/14≈0.929来近似α，则得到|nATA-nBTB|≈0.034，近似的精度提高了一个量级．数学上，通过对实数α=TB/TA进行连分数展开，可以系统性地给出所有关于α的有理数逼近；对于莫尔条纹，将恰好给出所有使式(4)近似为零的nA和nB．

2.2 连分数展开

任何一个正实数α都可以被表示成如下(简单)连分数展开的形式

(5)

可简写为[a0,a1,…,an,…]，其中展开系数an为正整数．一个有理数的连分数展开为有限阶，无理数的连分数展开为无穷阶．连分数展开是收敛的，其形式是唯一的，(对于一个有理数存在两种等价的表示形式：[a0,a1,…,an]与[a0,a1,…,an-1,1])，它是对于实数的一种“纯粹”的表示方式——其各阶展开系数与进制无关．本文主要利用连分数展开的以下性质，相应的证明可参见引文[10, 11]．

首先，将连分数[a0,a1,…,an,…]在第k阶截断，得到[a0,a1,…,ak]，等于分数pk/qk，被称为连分数的第k阶渐进分数，其中正整数pk和qk满足递推关系

(6)

可以证明，由式(6)定义的渐近分数pk/qk为既约分数；并且，随着阶数k增大，各阶渐近分数与α之差的绝对值严格递减且收敛于0．

第二，首先定义：对正实数α以及既约分数p/q，如果所有不大于q的正整数q′以及任意p′，都满足

|p′-αq′|≥|p-αq|

(7)

那么p/q是实数α的第二类最佳逼近．可以证明如下定理：α的连分数的各阶渐进分数pk/qk都是其第二类最佳逼近；并且，α的所有第二类最佳逼近都是其连分数展开的渐进分数．例如，2.1节中的13/14是0.931的第二阶渐进分数，可以验证，它是0.931的一个第二类最佳逼近．

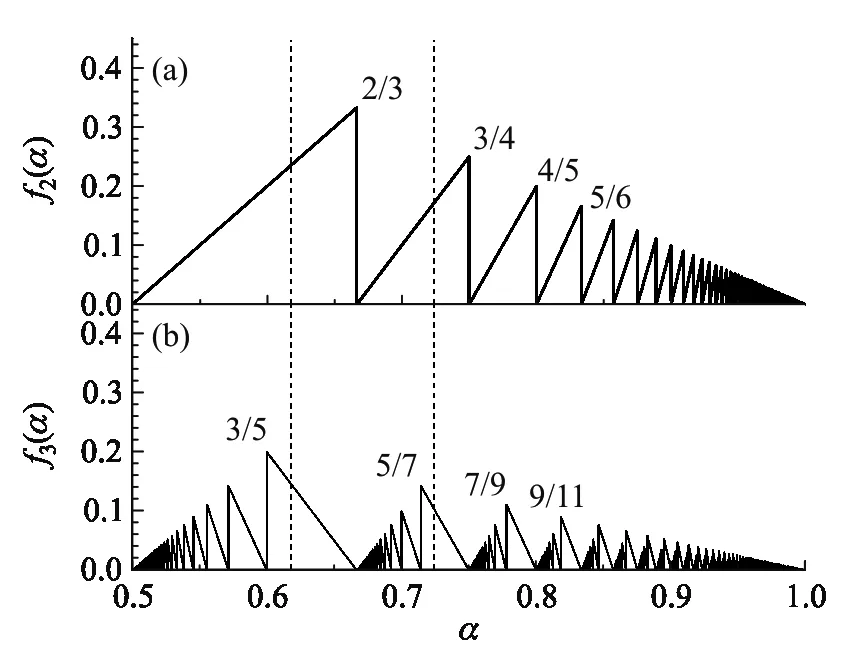
由上述定义和定理并对比式(4)、(7)可知，对于莫尔条纹，α=TB/TA的连分数展开的第k阶渐进分数pk/qk将正好给出使式(4)取其极小值的解：nA=pk，nB=qk；此处“极小值”的含义是指：第qk根B条纹与第pk根A条纹的间距小于第qk根B条纹之前任意第q′(0

式(4)、(7)在形式上的巧合，以及连分数的渐进分数与第二类最佳逼近的充要性，使得连分数展开自然而然地成为定义及计算莫尔条纹周期的最合适的数学方法．此外，我们指出，利用看似更为直接的第一类最佳逼近，无法给出符合实际观察结果的莫尔条纹周期．(第一类最佳逼近指的是：如果对于一个既约分数p/q，对任意q′≤q以及p′都有|p′/q′-α|≥|p/q-α|，则p/q是α的最佳逼近．可以证明，α的连分数的各阶渐进分数都是α的第一类最佳逼近；但并非所有α的第一类最佳逼近都是其渐进分数．)

2.3 各阶准周期

上述讨论表明，α=TB/TA的连分数的各阶渐进分数都可以对应一个莫尔条纹周期，且阶数k越小，莫尔条纹周期(pkTA或qkTB)越短，但|pk-αqk|越大，即近似程度越低．各阶准周期的表达式如下．为简化起见，我们令TA=1，且只讨论1/2

α的第1阶渐进分数为p1/q1=1/1，从而得到nA=nB=1，即TM≈TA≈TB，是一个平凡的、无意义的解．α的第2阶渐进分数为p2/q2=a2/(a2+1)，从而得到nA=a2，nB=a2+1，以及莫尔条纹的周期TM=a2TA，或等价的TM=(a2+1)TB．a2的数值为⎣α/(1-α)」，其中⎣x」表示x向下取整．如代入小数α/(1-α)=TB/(TA-TB)的值以近似计算a2，可得TM=⎣TB/(TA-TB)」TA．此式与式(3)几乎一致，最多相差一个TA．如果考虑更高阶的渐进分数，比如对于第3阶渐进分数有：α≈(a2a3+1)/(a2a3+a3+1)，得到莫尔条纹第3阶准周期TM=(a2a3+1)TA．以此类推，可以定义莫尔条纹的第k阶准周期TM=pkTA(或等价的TM=qkTB)．

在各阶准周期中，第2阶准周期最为特殊：只有在第2阶渐进分数α≈a2/(a2+1)的形式下，A条纹刚好比B条纹少经过一个周期而第一次达到近似重合的状态；并且，A条纹与其最近的B条纹的距离先单调增加后单调减小，这样的单次“亮-暗-亮”的变化最容易被人眼分辨．对于更高阶的准周期，其长度通常远大于2阶准周期长度，且每个周期内部还存在多次“亮-暗”的转变，对应于多个仅有微小区别的低阶准周期图案．所以人眼往往不易辨别出高阶准周期的存在，而通常能观察到的莫尔条纹的周期就对应于连分数的2阶渐进分数，也就是式(3)所给出的最为通用的表达式．但是我们还是指出，存在一些较为特殊的α，观察到的莫尔条纹周期确实对应于更高阶的渐进分数．

2.4 非周期程度

我们定义莫尔条纹各阶非周期程度fk(α)=|pk-αqk|(k≥2)，它表示A、B两组条纹经过一个第k阶莫尔条纹准周期后的间距与TA之比，反映了它们近似重合的程度．由连分数渐进分数的性质可知：低阶准周期非周期程度大，但周期短，所以易观察；高阶准周期的非周期程度小，即近似的精度高，但周期太长，不易观察．可见，实际观察到的莫尔条纹周期，在非周期程度(即精度)与准周期长度之间达到某种平衡．基于以上考虑，我们给出莫尔条纹周期的严格定义

TM=pkTA,k=min{k′},s.t.fk′(α)≤E

(8)

表示：k为满足fk(α)≤E的最小值，其中pk由式(6)的递推关系给出，而E是可观察到莫尔条纹周期的经验阈值．考虑到人类通常能够较为准确地分辨出一段给定长度的1/10，我们认为E比较合理的取值应在0.1左右．

f2(α)和f3(α)的图像如图2所示 ．对于某一阶fk(α)，其函数的图像形式为无数个直角三角形，每个直角三角形又刚好覆盖了高一阶的fk+1(α)的图像中一组面积依次改变的直角三角形．全体fk(α)函数表现出一种分形的自相似特征．由图2可知，当两组条纹的周期非常接近时(如α≥0.9)，f2(α)<0.1始终成立，所以莫尔条纹周期为第2阶准周期，基本上与式(3)等价．对于某些较小的α，经过一个2阶准周期后A条纹和B条纹重合程度不高，即f2(α)较大，而只有经过更高阶的准周期后，才满足fk(α)≤E，从而对应于人眼观察到的莫尔条纹．

图2 (a)2阶非周期程度f2(α);(b)3阶非周期程度f3(α)．虚线表示α=φ≈0.618以及α=φ2≈0.724

对于图1中所列举的各条纹周期之比，可验证，取E=0.1时，由式(8)定义的莫尔条纹周期与实际观察结果均相符：如图1(a)，α=0.9，f2(0.9)=0，表示两条纹严格重合，所以有TM=p2TA=9TA；图1(b)，α=0.901，f2(0.901)=0.01E而f3(0.714)=0.002E，f3(0.715)=0.14>E，而f4(0.715)=0.005

3 由连分数展开得到的推论

这一节，我们基于上述结果讨论几类特殊的条纹周期之比α及其莫尔条纹的周期性质．为验证理论推论，我们首先利用菲林打印机在透明塑料薄片上打印出由Ai软件绘制出的不同周期的条纹，随后将各组周期长度不同的条纹平行、重叠放置于一块平板LED灯前，用单反相机拍摄它们所构成的莫尔条纹(如图3、4)．

图3 具有严格周期性的莫尔条纹(实验照片)．周期比TB/TA分别为(a)2/3，(b)3/4，(c)3/5和(d)4/7，莫尔条纹的周期分别为：TM=2TA，3TA，3TA，4TA．其中(a，b)为二阶周期性莫尔条纹，(c，d)为三阶周期性莫尔条纹

图4 黄金比例莫尔条纹(实验照片)．TB/TA分别为(a) φ1=φ≈0.618，(b) φ2≈0.724，(c) φ3≈0.783，(d) φ4≈0.822

3.1 周期性二阶莫尔条纹

由上述莫尔条纹周期的连分数计算方法可知，若α=TB/TA的连分数为[0,1,a2]，即所有n>2的系数an均为0，那么其二阶渐进分数就等于α，此时由式(3)计算所得的周期是严格的，所形成的莫尔条纹的周期性也是严格的．满足这一条件的α具有a2/(a2+1)的形式(见图2(a))，即第1节中提到的使式(1)存在正整数解、且满足nB=nA+1的情况．此类周期性二阶莫尔条纹如图3(a)、(b)所示．可以看到，即便当α较小(如2/3)时也可以观察到明显的莫尔条纹，并且每个莫尔条纹周期都表现为简单的“亮-暗-亮”图样．当α在这些特殊比值附近时，显然也可以观察到较为明显的莫尔条纹现象．所以，通常认为只有当两组条纹的周期长度非常接近时才能观察到莫尔条纹现象的想法并不严谨．

3.2 周期性高阶莫尔条纹

若α=TB/TA的连分数为[0,1,a2,2]，此时其二阶渐进分数为a2/(a2+1)，当a2较小时f2(α)较大，所以不应直接由式(3)计算莫尔条纹的周期；而其三阶渐进分数(2a2+1)/(2a2+3)就等于α(见图2(b))，所以此类莫尔条纹也具有严格的周期性，其周期为(2a2+1)TA，属于三阶准周期(如图3(c))．类似的，若α=[0,1,a2,3]，即(3a2+1)/(3a2+4)(如4/7，7/10等)，莫尔条纹也存在严格的周期性(如图3(d))．在上述情况下，每个莫尔条纹周期表现为较为复杂的 “亮-暗-亮-暗-亮”图样．显然，当两组条纹的周期之比在上述这些特殊α值附近时，也可观察到这类更为复杂的高阶莫尔条纹准周期图案；而根据遮光原理的计算中要求式(2)成立，所以无法预言这一类周期性高阶莫尔条纹的存在．

以此类推，理论上，当α等于[0,1,a2,a3]甚至[0,1,a2,a3,2]等一系列类似数值时，莫尔条纹都具有高阶的严格周期性．当然事实上，当a2、a3数值较大时， 2阶准周期往往已经满足f2(α)

3.3 黄金比例莫尔条纹

与上述具有严格周期性的莫尔条纹相反，如果一个实数α的连分数展开具有无穷阶，且各阶系数都很小，说明任意一阶的渐进分数对α的逼近程度都较差，任意一阶的非周期程度都较高．其中最典型的是连分数[0,1,1,…]

(9)

如果式(9)中的第二阶系数略大于1，即连分数:

(10)

其中n为正整数，可以得到其他一系列与黄金比例密切相关的无理数．当n不太大时，这些数字同样较难用有理数逼近，各阶非周期程度都较高(见图2中的虚线)，可以想见它们对应的莫尔条纹的周期性也较差，我们称其为黄金比例莫尔条纹．如图4所示，各φn(n≤3)对应的条纹的周期性都不易分辨，只有当n继续增大，φn距有理数n/(n+1)的差距逐渐减小，条纹才开始显现出较为明显的周期性．正是因为连分数展开正确地揭示了莫尔条纹“准周期性”的本质，才能准确地预言这一系列特殊的无理数．

4 总结与展望

本文探讨了莫尔条纹的“准周期”结构与基于连分数展开的有理数逼近之间的深刻联系．研究发现，对于两组周期不等的平行条纹，它们叠加所形成的莫尔条纹具有各阶准周期，并恰好对应于两者周期之比的连分数的各阶渐近分数；其中，满足非周期程度低于经验阈值、即条纹重合精度足够高的最低阶渐进分数，是人眼所观察到的莫尔条纹．以上对莫尔条纹周期的严格定义，可避免过去通用的周期计算表达式在某些特殊情况下的错误结果．此外，基于连分数的有理逼近性质，可以建立起莫尔条纹非周期程度与实数基本特性之间的映射，从而可以系统性地分析出两类特殊的莫尔条纹：具有严格周期性的莫尔条纹，与各阶非周期程度都较大的黄金比例莫尔条纹．最后，我们指出，本文连分数展开的分析方法对所有周期性时空结构叠加的问题(如拍现象、历法置润等)都具有普适意义．

本文主要讨论了符合人眼观察结果的较为低阶的莫尔条纹，而连分数的各阶渐进分数可以系统性地预言周期叠加的全部性质，从而能帮助探索更高阶的准周期结构在凝聚态物理、信号处理等方面的潜在应用．本文只讨论了两组一维平行条纹的莫尔条纹现象．两组二维周期性网格能够叠加产生更为复杂的莫尔条纹，它们所形成的图样也具有类似的近似周期性，所以连分数展开的分析方法也可以推广到更高维度的莫尔条纹中．并且，本文给出了一组非周期程度最大的黄金比例莫尔条纹，黄金比例直接对应于五重旋转对称性的特征，(72°=360°/5，cos(72°)=φ/2)，而五重旋转对称性又是典型的准晶结构特征．这些巧合暗示着实数的连分数表示、莫尔条纹、晶体或准晶结构、超晶格，这些看似无关的数学、物理概念背后存在着非常深刻的联系，并且可能借由最新的转角电子学(Twistronics)的相关研究揭示出来[13, 14]．