一类多元Hermite型插值的离散化问题

姜 雪, 崔 凯

(1. 沈阳师范大学 数学与系统科学学院, 沈阳 110034; 2. 吉林大学 符号计算与知识工程教育部重点实验室, 长春 130012)

多项式插值问题在图像处理、 电子通信、 控制论和海洋气象学等领域应用广泛. 一元多项式插值理论包括插值函数的构造、 误差分析、 最佳逼近性质等， 目前已有较完善的结果[1]. 但多元多项式插值问题的研究还不完善, 其中一个重要原因是多元插值节点的结构较复杂, 每个节点上对应的插值条件也有多种形态[2-6]. 一元Lagrange插值是最简单的一类多项式插值, 其插值条件仅包含节点的函数值; 一元Hermite插值问题是指插值条件不仅包含节点处的函数值, 还包含节点处的连续阶偏导数. 在多元情形下, 仍有Lagrange插值的概念, 但Hermite插值的定义却不一致.

一元Hermite插值问题可视为Lagrange插值问题的极限形式. Shekhtman[7]证明了该结论在二元情形下也成立, 但对于三元及三元以上的情形, 总存在不能被离散的Hermite型插值问题. 类似于一元情形, 当多元Hermite型插值问题的插值条件仅由单项偏导条件构成时, 利用差分代替偏导数, 可将其离散为Lagrange插值问题的极限[8]. 目前, 关于Hermite型插值离散化问题的研究已有许多成果[9-14]. Hermite型插值离散化问题的实质是插值条件的离散. 本文将Hermite型插值问题转化为Lagrange插值问题的极限, 从而将复杂的问题简单化, 为构造复杂的多元插值问题的插值空间及给出误差公式提供一种新思路.

1 预备知识

spanF{δz∘q(D):z∈Z,q∈Qz}

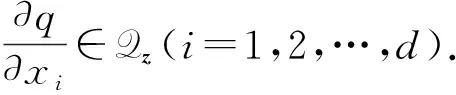
针对多元Hermite型插值问题, 如果每个节点对应的微分不变子空间诱导的微分算子均可以离散, 则该Hermite型插值问题可离散为Lagrange插值问题的极限.因此, 离散化问题可以逐点考虑.利用线性变换, 总可以假设插值节点z=0.对于任意给定单点的Hermite型插值问题, 设插值条件空间为

δ0∘Q0(D)∶={δ0∘q(D):q∈Q0}.

此外, 设有节点

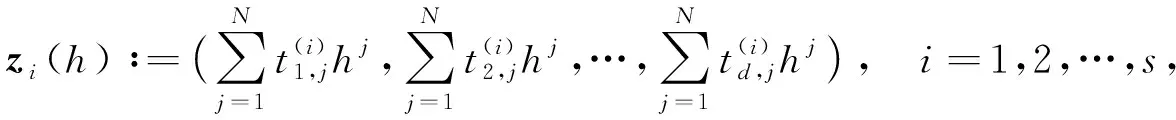
(1)

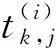
则zi(h)构成上述Hermite插值问题的离散节点.

对任意光滑的函数f,f(z(h))在0点的Taylor展开为

(2)

其中

pi为将式(2)视为h的多项式时hi的系数.对任意的正整数m, 令

基于上述记号, 文献[12]给出了如下离散逼近算法.

输入: 节点z=0, Qz=span{1,q1,q2,…,qs}, 其中deg(q1)≤deg(q2)≤…≤deg(qs);

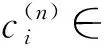
成立或“失败”.

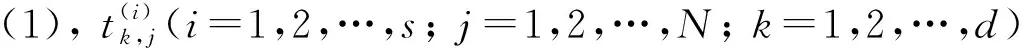
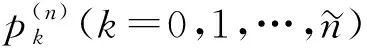
步骤3) 令

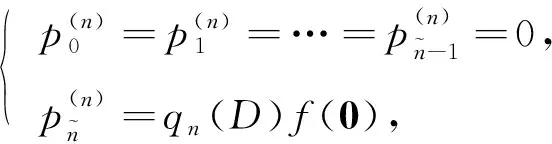
(3)

将式(3)确定的等式加入到S中, 置n∶=n+1;

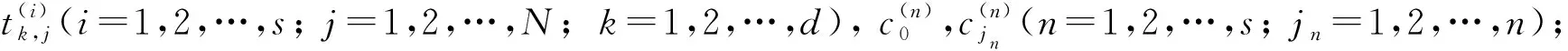
步骤5) 求解系统S, 若有解则选取S的一个特解, 并输出离散节点及系数, 否则返回“失败”, 算法终止.

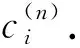
2 主要结果

由Q微分不变的性质可知, 1∈Q, 因此可假设Q基底中多项式不含常数项.对任意给定的二阶微分不变子空间

其中上角标表示多项式的次数.不失一般性, 利用变量替换并约掉常数项, 则任意微分不变子空间Q中的一次多项式均可表示为

(4)

其中x∶=(x1,x2,…,xd).基于上述记号, 文献[11]给出了二阶微分不变子空间基底中二次多项式的形式:

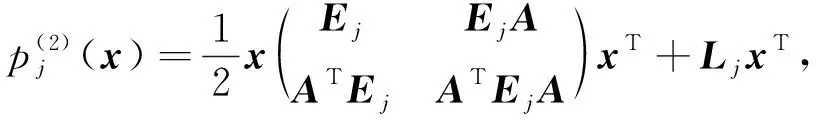
(5)

其中Ej为m1×m1对称矩阵,

为一个行向量.

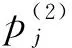
设节点z0(h)=0, 根据上述离散逼近算法可设空间Q对应下列离散节点:

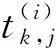
zi(h)=(ti,1h,ti,2h,…,ti,dh)=(ti,1,ti,2,…,ti,d)h,i=1,2,…,m+1.

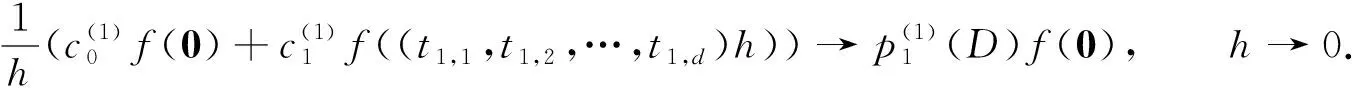
(6)

设

ek=(0,…,0,1,0,…,0)T∈Fm,k=1,2,…,m,

其中1位于第k个位置.记

ti=(ti,1,ti,2,…,ti,d),tih=(ti,1h,ti,2h,…,ti,dh),i=1,2,…,m+1,

则由式(2)可得

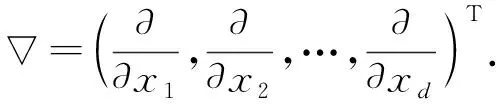
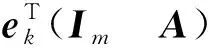
其等价于

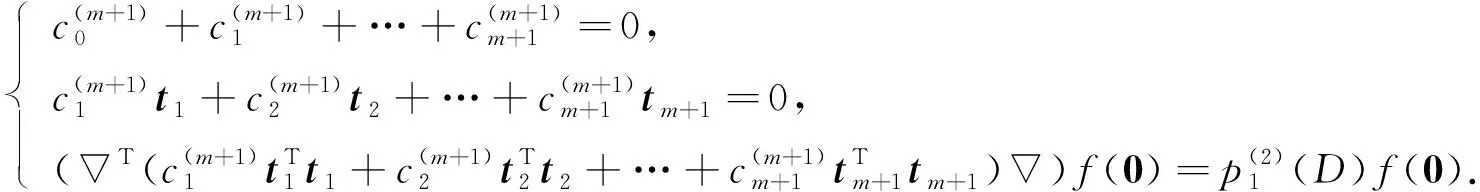
(7)

下面给出本文的主要结果.

定理2对任意给定的二阶微分不变子空间

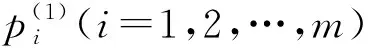
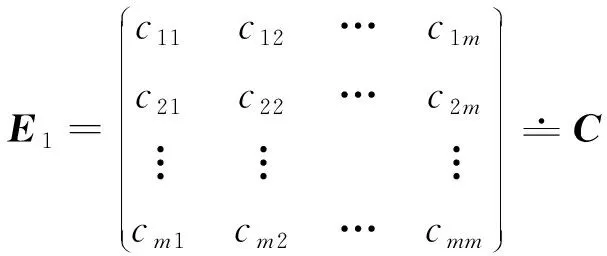
(8)

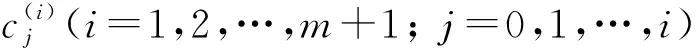
证明: 由上述分析可知, 在离散逼近算法思想下, 空间δ0∘Q(D)可被离散的充分必要条件是下列方程组有解:

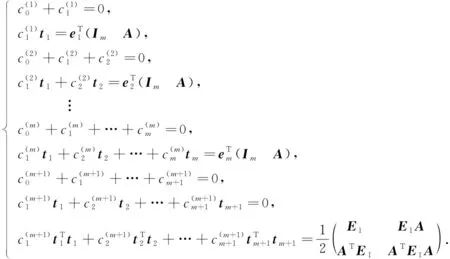
(9)

方程组(9)中最后一个等式成立是由定理1及

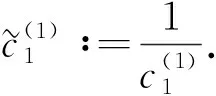
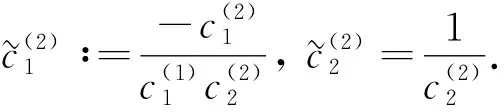
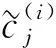
因此方程组(9)最后一个等式的左端为

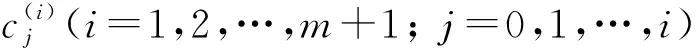
令其与式(9)右端相等可知结论成立.证毕.

推论1设有插值条件形如spanF{δz∘q(D):q∈Qz}的Hermite型插值问题, 且Qz具有定理2所述形式, 若方程(8)有解, 则该Hermite型插值问题可写成Lagrange插值的极限形式.

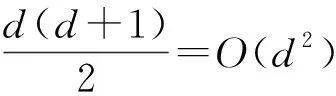
注2若所考虑插值问题对应的Qz基底中包含多个二次多项式, 则只需在方程组(9)中添加相应的等式再求解即可.

3 应用实例

定理2利用离散逼近算法的思想, 结合微分不变子空间的结构给出了二阶微分不变子空间对应的Hermite型插值问题可以离散的充要条件. 文献[11]由于事先确定了一阶离散节点, 得到的只是该问题的充分条件. 考虑文献[11]中的例3, 文献[11]给出的方法无法计算出其离散节点, 但利用本文定理2可以计算得到其离散节点.

假设有Hermite型插值问题, 插值条件构成的空间为

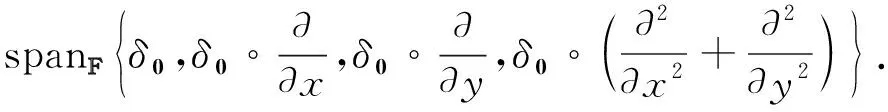
(10)

按本文理论,

Q=spanF{1,x,y,x2+y2},

根据定理2, 节点z0(h)=(0,0),zi(h)=(ti,1h,ti,2h)=(ti,1,ti,2)h(i=1,2,3)构成空间δ0∘Q(D)一组离散节点的充要条件是下列关于参数ti=(ti,1,ti,2)(i=1,2,3)及组合系数的方程组有解:

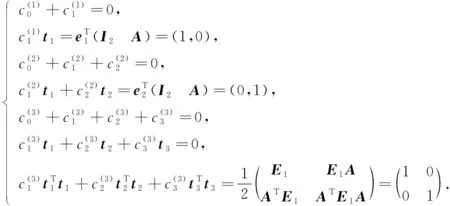
(11)

在MAPLE上求解方程组(11)并取其一组解, 可得离散节点:

z0(h)=(0,0),z1(h)=(h,0),z2(h)=(2h,2h),z3(h)=(2h,-5h),

即节点(0,0),(h,0),(2h,2h),(2h,-5h)上的Lagrange插值问题当h→0时收敛到插值条件形如式(10)的Hermite型插值问题.