Polaron and molecular states of a spin–orbit coupled impurity in a spinless Fermi sea∗

Hong-Hao Yin(尹洪浩), Tian-Yang Xie(谢天扬), An-Chun Ji(纪安春), and Qing Sun(孙青)

Department of Physics,Capital Normal University,Beijing 100048,China

Keywords: spin–orbit coupling,polaron,Fermi gas

1. Introduction

Coupling a mobile impurity to a many-body environment in a controllable way provides a handleable method to study the unique physics of emergent quasiparicles,e.g.,the polarons in diverse systems.[1–4]Among them the ultracold gases, being an ideal platform of high tunability and cleanness, have been utilized to explore the intriguing impurity physics[5–9]and many important advances have been achieved.[10–12]For examples, the realizations of Fermi polarons in spin-polarized Fermi gases,[13–35]the polarons in Bose–Einstein condensates (BEC),[36–40]and the polaron-tomolecule transitions,[41–44]which are usually surveyed by varying the interaction strength between the impurity atom and the surrounding atoms via Feshbach resonance.[45]

Recent years, the implementation of spin–orbit coupling (SOC) in ultracold gases[46–50]stimulates tremendous researches on the nontrivial effects brought by SOC,[51–60]which also enriches the content of the impurity physics in cold atom systems.[61–64]In general,SOC mixes different spin components of the atom and changes the single-particle dispersion dramatically, which may lead to the enhanced lowenergy density of state and possible single-particle groundstate degeneracy[46,60]responsible for the many-body behaviors of the underlying systems. A series of Fulde–Ferrell–Larkin–Ovchinnikov-like molecule states are predicted in different impurity models with SOC.[61,62]Nevertheless, previous works focus on the cases that the SOCs are mainly introduced to the majority atoms of the environment.[62,63]Due to the heating problem caused by the Raman lasers to generate SOCs in current experiments,[55]it would be difficult to reach the degenerate regime of the majority atoms especially for the Fermi gas.

In this paper,we consider a different situation that a onedimensional (1D) SOC is introduced solely to the impurity atom,which is immersed in a three-dimensional(3D)spinless Fermi sea formed by the majority atoms. One of the advantages of this configuration is that the majority atoms are not affected directly by the Raman lasers avoiding heating,and thus facilitates the investigation and manipulation of the impurity states by SOC.To be specific,in this system,we find that SOC can strongly affect the polaron state via the impurity atom,with the ground state always carrying a finite c.m. momentum. Due to the SOC induced double-minimal structure of the energy spectrum, a first-order transition may occur between two polaron states with different center-of-mass (c.m.) momenta,in contrast to previous works where a zero-momentum polaron is considered.[59–61]Meanwhile,the molecular state is also changed by the SOC,giving rise to a unique polaron-tomolecule transition driven by the Raman coupling. The quasiparticle residue and the effective mass of the polaron,as well as the mass ratio effect are also discussed. Our results suggest a new way to study the impurity physics brought by SOC.

The paper is organized as follows: In Section 2,we give the Hamiltonian to describe a spin–orbit coupled impurity atom interacting with a spinless Fermi sea. In Section 3, we analyze the unique properties of the polaron state, including the energy dispersion,the ground-state momentum,the quasiparticle residue,and the effective mass.Moreover,the groundstate transition of the polaron with different c.m. momenta is also discussed. In Section 4,we further present the results of the molecular state and the polaron-to-molecule transition. Finally,we discuss the effects of a more general spin-dependent interaction and mass ratio and conclude in Section 5.

2. The model

We consider a spinful fermionic(impurity)atom of massmaimmersed in a spinless 3D Fermi sea of massmb. A one-dimensional (1D) SOC is introduced into the two spin states (labeled asσ=↑,↓) of the impurity by a pair of Raman lasers[46]or recoil-dressed photons.[58]In the momentum space, the total Hamiltonian of the system takes the form of(we set ¯h=1)

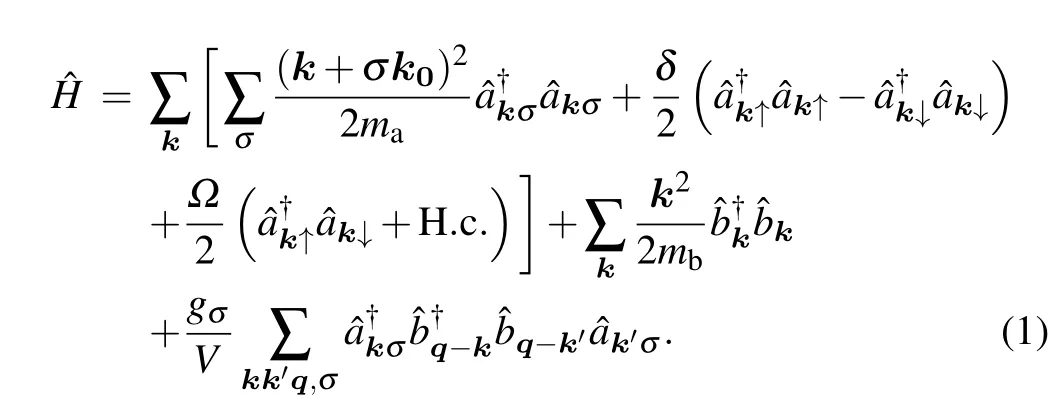
Here, ˆakσand ˆbkare the annihilation operators of the impurity atom with spinσand the majority atoms forming the Fermi sea,respectively.2k0is the momentum transfer characterizing the strength of SOC,andδandΩdenote the effective Zeeman splitting(two-photon detuning)and spin flipping(Raman coupling)between the two spin states of the impurity, which can be tuned in experiment.[46,47]gσ(<0)describes the strength of the contact attraction between the impurity atom of spinσand the majority atoms, while the interaction between impurity atoms is absent in the single impurity limit. In the following, we first consider a spin-selected interaction by assumingg↑≡gandg↓=0,which can be readily achieved via Feshbach resonance.[45]A more general situation with spin-dependentg↓/=0 is discussed later, where the main physics obtained atg↓=0 is not changed significantly up to a considerableg↓. In 3D case,the bare interactiongis renormalized as[65]

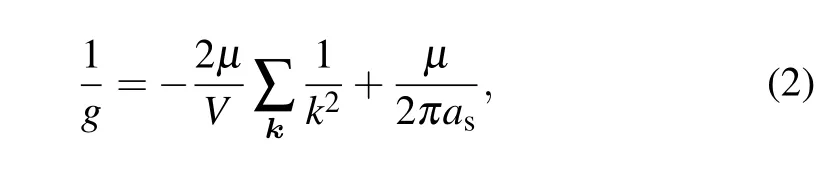
whereasis the s-wave scattering length, ranged from the BEC side withas> 0 to the BCS side withas< 0.µ=mamb/(ma+mb) is the reduced mass andVis the quantized volume.

3. Polaron state

In the limit of single impurity, the free impurity atom is scattered by the atoms in the Fermi sea to form a dressed state—Fermi polaron,[30]which can have a lower energy than the free impurity state and is expected to be the ground state of this system for a weak attractive interaction. Up to a particlehole fluctuation, the variational wave-function of the polaron with c.m. momentumQcan be constructed as

whereφσandφkqσare the amplitudes of a bare impurity of spinσand that dressed by a particle–hole excitation, respectively. In Eq. (3), we have included both spin states of the impurity atom,which are mixed due to the introducing of 1D SOC.[62]The summation of momentum is limited toqkF(particle) withkFbeing the Fermi momentum of the Fermi sea|FS〉Nformed byNatoms. Minimizing〈P| ˆH −EP|P〉Qwith respect toφσandφkqσ, we can obtain the polaron energyEP(relative to the Fermi sea),which is determined by the following equation(see Appendix A for more details):

The left-hand side of Eq. (4) describes the energy correction onEPfrom SOC while the right-hand side gives the contribution from the interaction. In what follows, we usek0=|k0|and the corresponding energyε0≡(k20/2ma) as the units of momentum and energy,respectively.

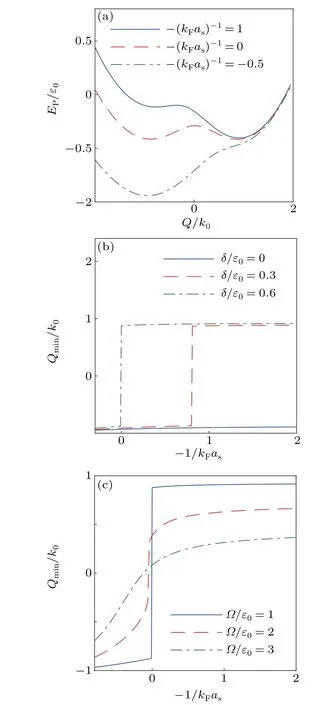
Fig. 1. (a) The polaron energy dispersion EP with the momentum Q along the direction of SOC for different interaction parameters −1/(kFas) with Ω/ε0=1 and δ/ε0=0.6. (b)The ground-state momentum Qmin as a function of −1/(kFas)for different δ with Ω/ε0 =1. (c)The ground-state momentum Qmin as a function of −1/(kFas) for different Ω with δ/ε0 =0.6.Here,we have chosen k0=kF.

Solving Eq. (4) for eachQ, we can obtain the energy dispersion of the polaron. As shown in Fig. 1(a), a doubleminimum structure of the polaron dispersion is found to be along the direction ofk0due to the SOC, and the lower one gives a nonzero ground-state momentumQmin=Qminˆk0with ˆk0being the unit vector ofk0,where the ground-state energy of the polaron is lower than the free impurity state. More interesting,by varying the interaction strength(scattering lengthas),the minimum with a higher energy may become the lower one,giving rise to a discontinuous change ofQminbetween the two minima. In Fig.1(b),we plot the ground-state momentumQminas a function of interaction strength for different Zeeman splittingδ. One can see that for finiteδ,Qminjumps abruptly at a critical interaction strength which increases withδ(the red-dashed and green-dash-dotted lines in Fig.1(b)).Such discontinuous transition would be smoothened by further increasing the Raman coupling strengthΩ,and become a continuous one forΩ/ε02 (referred to the green-dash-dotted line in Fig. 1(c)). Physically forδ>0, the (right) minimum with a larger weight of↓-component would be the ground state in the weak interaction limit(as<0),which is weakly dependent on the spin-selected interaction. On the other hand for a sufficiently large interaction strength, the impurity would occupy the (left) minimum with a larger weight of↑-component by lowing the interaction energy to compensate the energy costδ. Notice that forδ= 0, such transition is absent and the interaction always favors the minimum state with a larger↑-component.

Fig.2. (a)The quasiparticle residue Z(Z↑/↓)as a function of −1/(kFas)with δ/ε0 =0.6 and Ω/ε0 =1. (b) The effective mass m∗/ma as a function of−1/(kFas)with other parameters the same in panel(a).

Above picture becomes more transparent when we examine the quasi-particle residueZ ≡∑σ ZσwithZσ=|φσ|2,which is given by(see Appendix B for detail)

In Fig.2(a),we give a typical evolution ofZwith the interaction strength forΩ/ε0=1 andδ/ε0=0.6. Across a critical value, an abrupt jump ofZindicates the discontinuous transition of the ground-state momentum of the polaron. Meanwhile, the state-dependent residueZσalso exhibits a sudden change with a largerZ↑(Z↓) in the regime of relative strong(weak) interaction. Moreover, due to the spin-selected interaction,Z ≃1 in the weak interaction regime and decreases quickly in the strong interaction regime(as>0)after the transition,where the influence of particle–hole excitation becomes significant. Such unique behaviors ofZcan be readily measured in experiment.[19]

Another measurable quantity to characterize the above physics is the effective mass of the polaron,defined as

Due to the anisotropy of the energy dispersion,m∗is generally anisotropic and we are interested in the component along ˆk0.As shown in Fig.2(b),we present the relative ratiom∗/maas a function of interaction strength. Forδ>0,a similar discontinuous behavior is expected to occur at the critical point. In the limit ofas<0,the impurity atom is only weakly affected by the interaction andm∗/ma→1. While in the BEC regime withas>0, the impurity is strongly dressed by the particle–hole excitations, and the effective mass is greatly enhanced towards the instability to the formation of a molecular state discussed in the following.apparently. Moreover,such dependence ofqminonasbecome stronger for a largerδ(Fig.3(a))orΩ(Fig.3(b)). Overall in the presence of the 1D SOC,the molecular state is much less affected than the polaron.This is because that the molecule appears in the strong interaction regime withas>0, where the spin-selected interaction binds the impurity in|↑〉state with one atom in the Fermi sea tightly. This is in contrast to the polaron state dominant in the weak interaction regime,where the single-particle state of the impurity plays a more important role, and thus more sensitive to the spin splittingδand spin flippingΩ.

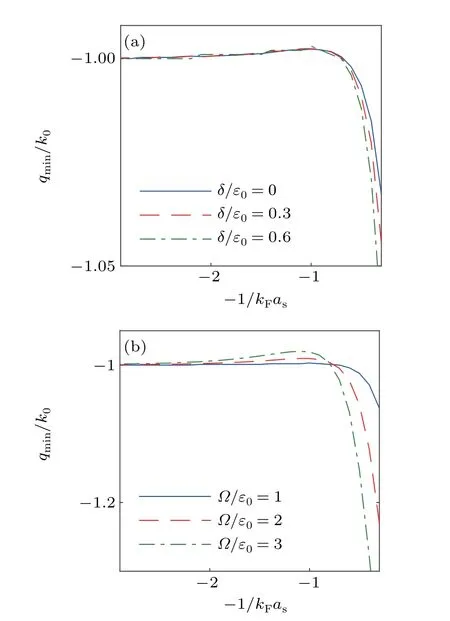
Fig. 3. (a) The molecular ground-state momentum Qmin as a function of−1/(kFas) for different Zeeman field δ with Ω/ε0 =1. (b) The molecular ground-state momentum Qmin as a function of −1/(kFas) for different Raman coupling strength Ω with δ/ε0=0.6.

4. Molecular state and polaron-to-molecule phase transition

When the interaction is strong,a molecular state may appear by tightly binding the impurity atom with one of the majority atoms on top of the Fermi sea. The variational wave function of the molecule with c.m. momentumqcan be written as

The ground state of the molecule is determined by further minimizingEMwith respect toq.

Similar to the polaron state,the SOC can also induce a finite c.m. momentumqmin=qminˆk0on the ground state of the molecule. As shown in Fig.3,in the BEC limit(as→0+),we haveqmin/k0→−1 irrespective ofδandΩ,and with the increasing ofas,|qmin|first decreases slightly and then increases

With the polaron and molecular states in hand, we can readily obtain the ground-state phase diagram of the system by comparing the energies of both states. In Fig. 4(a), we show the phase diagram in the−(1/kFas)–Ωplane. ForΩ= 0,δgives the same energy shiftδ/2 for bothEPandEM, and hence do not change the critical point. With the increasing ofΩ, the phase boundary is pushed into the deep BEC regime gradually, suggesting that the polaron state is more favorable for largeΩ. On the other hand, the phase boundary is only weakly dependent onδ(Fig.4(b)). This can be explained that from Eqs.(4)and(9),the main energy corrections caused byδare almost the same forEPandEM,whileΩcorrectsEPmore significantly thanEM. Given this,one may address the unique polaron-to-molecule transition by tuning the Raman coupling(spin flipping)Ωin experiment.

Fig. 4. The ground-state phase diagram (a) in the −1/(kFas)–Ω plane for different δ,and(b)in the −1/(kFas)–δ plane for different Ω. Here,P and M denote the polaron and molecular states respectively.

5. Discussion and conclusion

Above we have discussed the case ofg↓=0. For a more general spin-dependent interaction withg↓/=0, we find that the energy dispersion of the polaron state bears similar double minima structure for differentg↓/g↑, as shown in Fig. 5(a).Correspondingly, the ground-state momentum of the polaron shows a similar behavior as that ofg↓=0 (see Fig. 1(c) and Fig.5(b)),i.e., it exhibits a discontinuous transition for smallΩ/ε0=1 while varies continuously for largeΩ/ε0=3. The main change is that the transition point moves to the BEC side for a largerg↓, which can be also clearly identified from the effective mass of the polaron shown in Fig. 5(c). These results suggest that a finiteg↓/g↑<1 would not change the main physics of the polaron state significantly. In Fig.5(d),we give the phase diagram of the system.With the increasing ofg↓/g↑,the phase boundary is pushed towards the BCS side,indicating that the molecular state is more favorable for a largerg↓.

Fig. 5. (a) The energy dispersion EP of the polaron as a function of Q for different g↓/g↑=0 (blue solid), 0.5 (red dashed), and 0.9 (green dashdotted). (b) The minimal momentum Qmin as a function of −(1/kFas) for different Raman coupling strengths Ω =1 (blue solid) and 3 (red dashed)at g↓/g↑=0.5. (c) The effective mass m∗versus the interaction parameter for different g↓/g↑=0 (blue solid), 0.5 (red dashed), and 0.9 (green dashdotted). (d)The ground-state phase diagram in the −(1/kFas)–g↓/g↑plane.Other parameters are Ω/ε0=1 and δ/ε0=0.6 if needed.

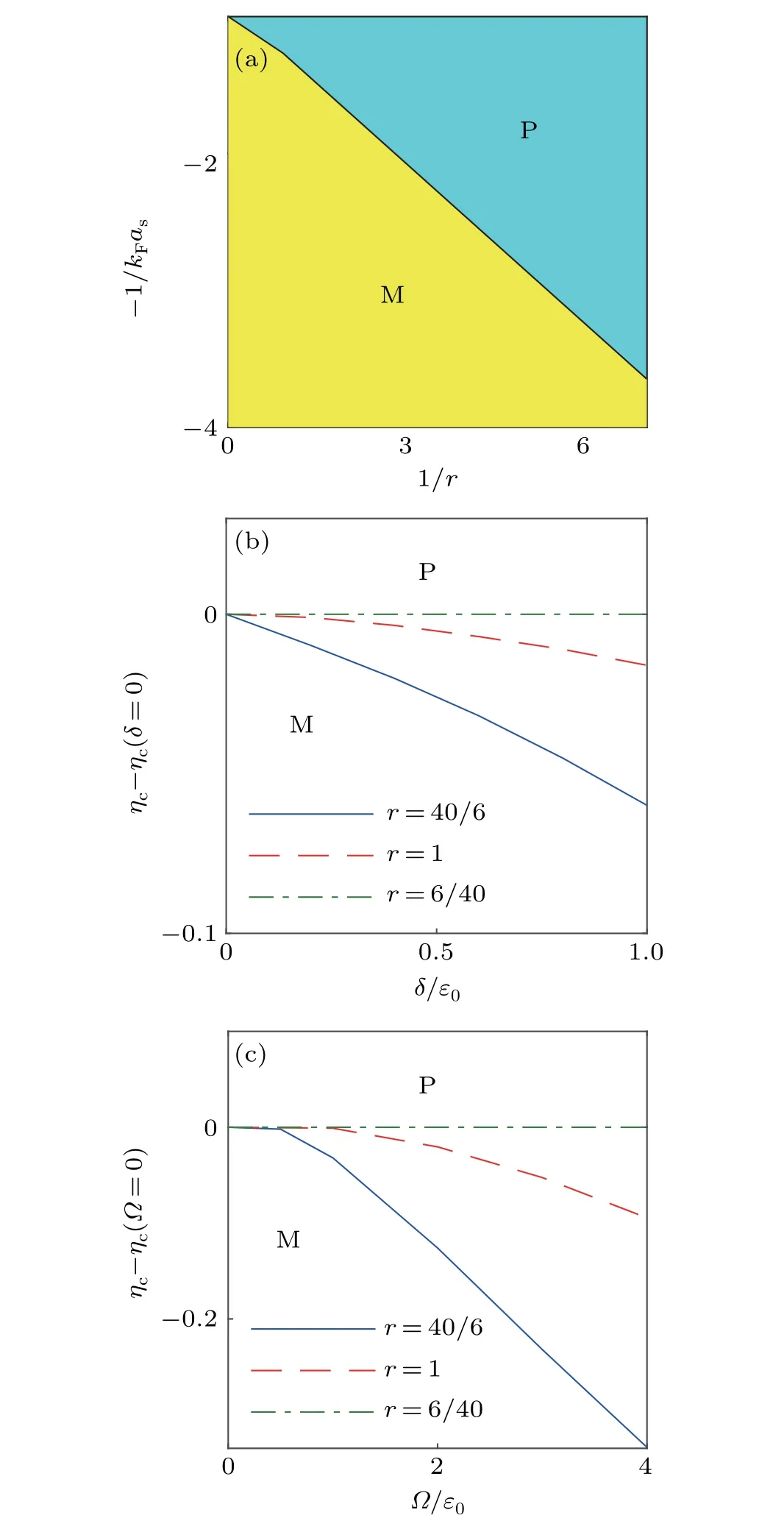
Fig.6. (a)The evolution of the phase boundary in the −(1/kFas)–1/r plane with Ω/ε0 =1 and δ/ε0 =0.6. (b) The critical interaction parameter ηc as a function of Zeeman feild δ with Ω/ε0 =1. (c)The critical interaction parameter ηc as a function of Raman coupling strength Ω with δ/ε0=0.6.

So far we have focused on the situation that the impurity atom and the majority atoms are of equal mass, which can be achieved by using different hyperfine states of the same species. In experiment,it is also possible to realize a mixture of different species with unequal mass,for example,a mixture of6Li and40K with mass ratior ≡ma/mb=6/40 or 40/6. As shown in Fig. 6(a), in general, the critical interaction parameter (as) of the polaron-to-molecule transition decreases with the inverse of the mass ratio 1/r,suggesting that a light impurity is more favorable to form a polaron than a heavy one. In Figs.6(b)and 6(c),we further investigate the transition point which is characterized byηc(x)−ηc(0)withη ≡−(1/kFas)as a function ofx=δorΩfor different mass ratios. It can be seen that the phase boundary of a heavy impurity is pushed into the BEC regime considerably with the increasing ofδorΩ(see the blue solid line ofr=40/6),while a light impurity is not affected apparently byδandΩ(referred to the green dash-dotted line ofr=6/40). Note that forΩ=0, the onedimensional SOC can be gauged away and one gets the usual critical value of−(1/kFas)～−3.65 without SOC.

Compared to the previous work[61–64]where molecule states with a finite c.m. momentum are induced by the SOC,here in our case,the one-dimensional SOC of the impurity has more profound effect on the polaron state than the molecule state. When a high-dimensional SOC is introduced to the impurity atom,the enhanced single-particle ground-state degeneracy may also affect the molecule state strongly with unique features(For an impurity atom with two-dimensional Rashbatype SOC, the ring degeneracy of the single-particle state of the impurity may greatly enhance the pairing between the impurity and the atom in the Fermi sea with an unusual molecule state appearing even in a weak interaction regime),which nevertheless is out of the scope of the current work and we leave it for the future study.

In a summary,we theoretically investigate the properties of the polaron and molecular state of a spin–orbit coupled impurity in a three-dimensional Fermi gas. A couple of polaron and molecule states with finite c.m. momenta, which arises from the interplay between SOC and spin-selected interaction,are found to be the ground state. A discontinous transition between these polaron states is identified and manifested in the quasi-particle residue and effective mass of the polaron.Moreover, the polaron-to-molecule transition and the effects of a more general spin-dependent interaction and mass ratio are also discussed. These results pave a new way to study the interesting impurity physics brought by the SOC.

Appendix A:Derivation of the polaron state

From Eqs.(A9)and(A10),we find

Finally,we get the equation of the poalron energyEP,

Forg↓=0,we recover the energy Eq.(4)in the maintext.

Appendix B: Quasiparticle residue of the polaron state

The total quasiparticle residueZ=Z↑+Z↓comprised of the contributions of different spin states withZ↑=|φ↑|2andZ↓=|φ↓|2. Here we focus on the case ofg↓= 0. From Eq. (A7), we haveZ↓=(Ω2/4)(EP−ε↓+δ/2)−2Z↑. And the normalization condition becomes

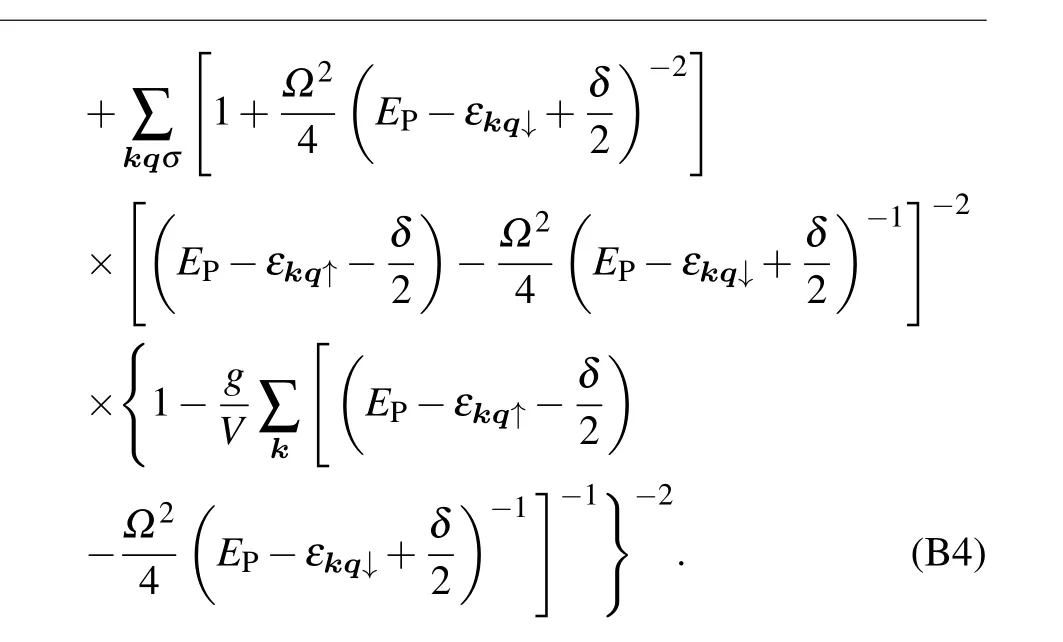
whereηk=(EM+EF−εk↓)(EM+EF−εk↑)−Ω2/4. From Eqs.(C4)and(C5),we get

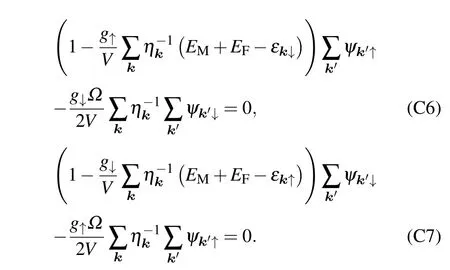
Finally, the self-consistent equation of the molecule energy is

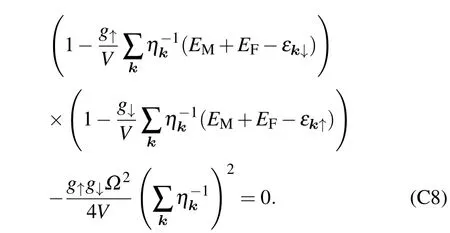
Similarly,we go back to Eq.(9)in the maintext forg↓=0.

Next, we calculateψkσforg↓=0. From Eq. (C4), we obtain