Collapse arrest in the space-fractional Schr¨odinger equation with an optical lattice∗

Manna Chen(陈曼娜) Hongcheng Wang(王红成) Hai Ye(叶海)

Xiaoyuan Huang(黄晓园)1, Ye Liu(刘晔)1, Sumei Hu(胡素梅)2, and Wei Hu(胡巍)3

1School of Electrical Engineering and Intelligentization,Dongguan University of Technology,Dongguan 523808,China

2Department of Physics,Guangdong University of Petrochemical Technology,Maoming 525000,China

3Guangdong Provincial Key Laboratory of Nanophotonic Functional Materials and Devices,South China Normal University,Guangzhou 510006,China

Keywords: soliton solution,collapse,variational approach,nonlinear Schr¨odinger equation

1. Introduction

Collapse is a universal nonlinear phenomenon,which has attracted considerable theoretical and experimental interests in physics.[1–4]It may occur in plasma waves,[5]Bose–Einstein condensates or matter waves,[6]capillary-gravity waves on deep water,[7]and even in astrophysics.[8]In optics, collapse refers to fact that an optical beam may evolve into spikes of infinite amplitude in a finite propagation distance due to selffocusing effect. Though such a phenomenon has drawn much interest with applications including ultrashort laser pulse,[9]it is often harmful for laser equipments because it causes filamentary damages in transparent materials. Typically, effects such as discreteness,[10,11]periodicity,[12]non-paraxiality,[13]nonlocality[14]and saturated nonlinearity[4]can completely resist occurrence of collapse.

On the other hand, the fractional Schr¨odinger equation (FSE) was first proposed in quantum mechanics by Laskin.[15–17]It includes a fractional Laplacian operator instead of the conventional one in the classical Schr¨odinger equation. In optics, a plenty of new features stemming from the fractional order of space derivative are numerically found in the evolutions of optical beams. For instance,the linear FSE supports irregular beam propagations, such as zigzag trajectory,[18]conical diffraction[19]and splitting behaviors.[20–22]When the fractional order equals 1/2, the FSE describes the beam evolution in a honeycomb lattice.[23]In the nonlinear FSE, the stability of optical solitons can be enhanced through modulation of the fractional Laplacian operator.[24–26]

The collapse is traditionally known to take place in a twoor more-dimensional nonlinear system. Recently,the collapse was found in a system described by the one-dimensional(1D)FSE.[27,28]In particular,it has been shown that these two types of collapse have similar physical realization conditions.[28,29]Although the collapse has been under active investigation,its arrest has never been explored in the FSE.

In this article,suppression of collapse in the FSE with an optical lattice is investigated. The variational method is used to predict the properties of soliton solutions, which nicely fit the numerical results. The stability analysis is also given and confirmed by the numerical simulations. The energy criterion shows that the collapse is prohibited by optical lattice when the perturbations is small enough. The profiles of solitons during propagation show that the collapse is prohibited for the focusing effect of the lattice potential occurring faster than the self-focusing collapse.

2. Variational approach for nonlinear fractional Schro¨dinger equation with a lattice potential

Our model is based on the FSE for evolution of a 1D paraxial beamΨ(x,z) in aspherical optical cavities proposed by Longhi.[30]In such cavities, we replace the second phase mask with a transparent thin slab with Kerr nonlinearity and an external lattice potential.[31]Thus the dimensionless FSE becomes

andC=0, whereAsis the soliton amplitude,β=b/zis the propagation constant. Based on Eqs. (5), (11) and (12), the approximate soliton solution of nonlinear FSE with a lattice potential can be obtained.

To verify these soliton solutions of variational approach,we numerically solved Eq. (3) by the squared-operator iteration method. We compare Eqs. (11) and (12) with the exact numerical results forV0=0.5, as shown in Fig. 1. Here we define the numerical soliton rms widthwas

Figures 1(a)–1(d) demonstrate that the variational approach provides a good overall agreement with the numerical results.The accuracy is better for lagerαcase than for the smallerαcase. Figures 1(e) and 1(f) display typical exact soliton solutions, which have a single hump located at the bottom of the potential. This means that the solitons are confined to the peak of the refractive index. One can see that the solitons are always confined to one lattice site. For a fixedα, increasing propagation constantβresults in a more confined soliton.Therefore, the discrepancy is reasonable for the fact that our Gaussian profile provides less stringent envelope to match the exact one.

Fig.1. Soliton amplitude As [(a),(b)]and propagation constant β [(c),(d)]versus soliton width w,respectively(curves: the analytical results obtained by the variational method;symbols: the numerical results). [(e),(f)]Profiles of numerical fundamental soliton solutions for different values of propagation constants. Upper: α =1.3. Lower: α =1.6. Here V0=0.5 and Ω =1.

3. Stability of soliton and collapse arrest

To analyze the stability of these fundamental soliton families, we consider the perturbed solution to Eq. (1) in a form ofΨ(x,z) ={ψ(x)+[u(x)+v(x)]exp(λz)+[u∗(x)−v∗(x)]exp(λ∗z)}exp(iβz),whereu(x),v(x)≪1,andλis the eigenvalue of perturbations. Linearizing Eq. (1) around stationary solutionψ(x),we obtain the linear-stability eigenvalue problem:

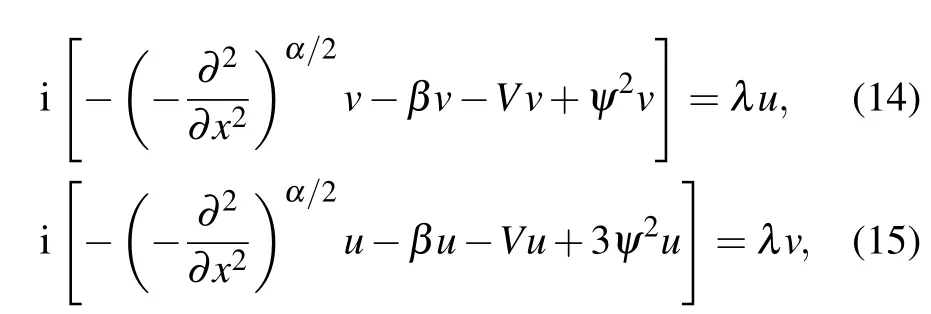
whose eigenvalues can be computed by the Fourier collocation method.[34]We find that the soliton families for 1<α ≤2 contain purely imaginary eigenvalues and thus they are completely stable. We also verify the stability prediction by performing numerical simulations using the split-step Fourier method. The soliton families are robustly stable against 1%random-noise perturbations in initial amplitudes.No collapses are found when 1<α ≤2. The representative examples of evolution are displayed in Fig. 2. Note that the stability of solitons is better than other lattice cases in the nonlinear FSE.[24,35]

We further focus on the limited caseα=1. Note that without lattice potential, the solitons atα= 1 would selffocus and eventually collapse when the power above a critical threshold, which is also the soliton power.[28]Such collapse behavior in 1D FSE is similar to the counterpart in the 2D SE.In the presence of periodic potential, the solitons are linearly stable in the entire existence domain. However,this does not guarantee that these solitons will not collapse under small perturbations. Recalling that in the 2D case, the collapse can be prohibited for a positive energy (i.e.,E>0) under small perturbations.[12,36]

Fig.2. Evolutions of solitons at β =3.5 with 1%random-noise perturbations in initial amplitudes for(a)α=1.3,(b)α=1.5,and(c)α=1.8.V0=0.5,and Ω =1 in all the panels.

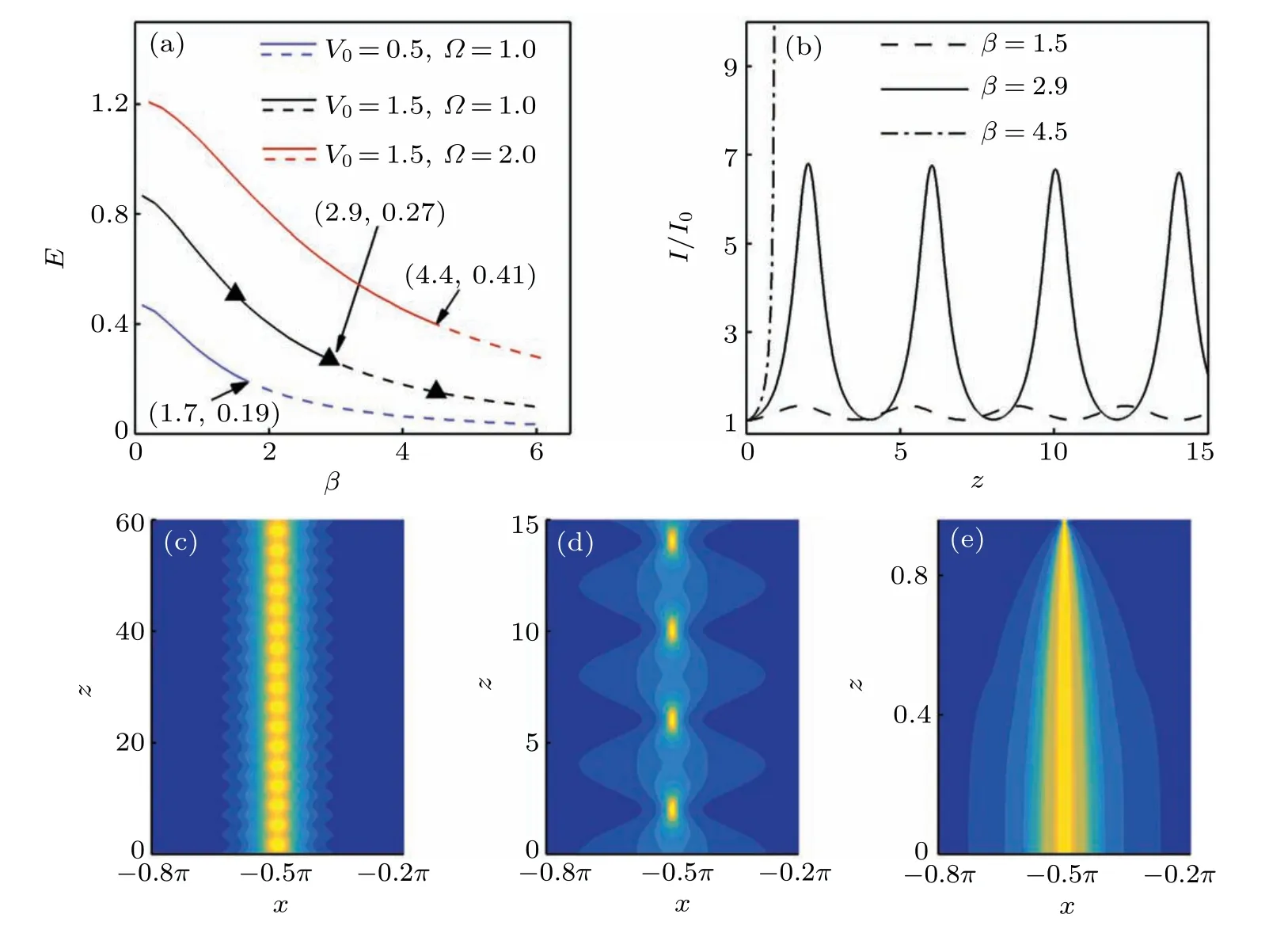
Fig.3. (a)Energy E of soliton versus propagation constant β for different values of V0 and Ω. Solid: collapse is resisted. Dashed: collapse occurs. (b) Normalized on-axis intensities [I0 =I(0)] versus the propagation distance for solitons at different β values [corresponding to solitons marked as the triangular symbols in panel (a)] against perturbations ε =0.01 and ψp =1. (c)–(e) Evolutions of these solitons (for β =1.5,β =2.9,and β =4.5,respectively). Here α =1 for all panels.

Fig.4.(a)Normalized on-axis intensities of soliton versus the propagation distance for β =4.5 and β =6.1.[(b),(c)]Their simulations against perturbations ε =0.001 and ψp=1. Here α =1,V0=1.5,and Ω =1 for all panels.

For the 1D case with lattice potential,Fig.3(a)shows that the energyEdecreases with increasingβ. TheE>0 holds for all soliton solutions. Therefore, we expect that the collapse can be arrested by the lattice potential against small perturbations. To prove this issue, we study the soliton evolutions by performing direct simulations of Eq. (1) with initial inputΨ(x,0)=ψ(x)[1+εψp(x)], whereε ≪1, andψpis the perturbations. We setε=0.01 andψp=1. Figure 3(b) shows illustrative examples of on-axis intensities versus propagation distance,and their corresponding propagations of solitons are displayed in Figs.3(c),3(d),and 3(e). We find that the soliton only collapses when the energy satisfyE ≤Ec(whereEc>0),that is,the collapse is prohibited,and the soliton becomes stable forE>Ec[see Figs.3(c)and 3(d)],while it collapses forE ≤Ec[see Fig. 3(e)]. The collapse energy thresholdEcis marked in Fig.3(a),and its increases with the lattice depthV0or frequencyΩ. However,the collapse forE>Eccan be prohibited if the amplitude of perturbation becomes small enough.

The on-axis intensity undergoes sine-like oscillations and the solitons become stable, as shown in Fig. 4 for perturbationsε=0.001. In other words, the suppression of collapse is dependent not only on the positive energy, but also on the magnitude of perturbations. Such criterion of collapse arrest in the 1D FSE case is similar to that in the 2D SE case.

We next discuss the physical mechanism of lattice potential preventing the collapse suppression. For this purpose,we monitored the transverse structure of solitons at each maximum or minimum of its on-axis intensity.When the collapse is arrested, the perturbed soliton distribution oscillates in width and height,and yet still be bell-shaped within a lattice site[see Fig. 5(a)]. At each maximum of on-axis intensity, we found lower hump confined in each lattice site adjacent to the inner bell part[see Fig.5(b)]. These lower humps are formed due to the lattice potential, which induces the focusing effect being faster than the self-focusing collapse. The formation of lower humps also plays an important role in leaving the power in the inner part less than the critical threshold,and eventually leading to the prohibition of collapse. Moreover,one observes the radiative decay beyond the lower humps,as shown in Fig.5(c).Such radiative wave carries a negligible power, which cannot be refocused or drawn into the inner part by the focusing effect, and thus ensures the prevention of collapse. Similar situations can be found in Ref.[37]for the 2D cubic SE with a Gaussian potential.

Fig. 5. (a)–(c) Transverse profiles at maximum or minimum of on-axis intensity, corresponding to the soliton evolution in Fig. 3(c). (d)Transverse profiles at the first maximum of on-axis intensity,corresponding to the soliton evolution in Figs.3(e)and 4(b).

The collapse is prohibited for the focusing effect of the lattice potential, which occurs faster than the Kerr selffocusing collapse. To further prove this numerical issue, we compare the soliton profile at the distance of collapse occurring with that at the maximum of height in the collapse arrest case, as shown in Fig.5(d). When the collapse is prohibited,the significant bell-shaped part lies within a lattice site(dashed line), while it splits into spikes of large amplitude when collapse occurs (solid line) for large perturbations. Note that these profiles evolve from the same input soliton profile while with different magnitudes of perturbations. Therefore,the occurrence of self-focusing collapse is accelerated by the larger amplitude of perturbations,so that it is faster than the focusing due to the lattice potential and leads to the collapse.

4. Conclusion

In summary, we have studied the fundamental solitons and the suppression of collapse in the 1D FSE with the Kerr nonlinearity and the lattice potential. The approximate analytical soliton solutions are obtained based on the variational method, which provides reasonable accuracy. The stability analysis has shown that all solitons are linearly stable and confirmed by the numerical simulation. The collapse atα=1 is numerically proved to be suppressed for the positive energy with a small amplitude of perturbations as its 2D SE counterpart. The physical mechanism of collapse arrest is that the focusing effect of the lattice potential occurs faster than the self-focusing collapse. We believe that our study is helpful for understanding the FSE,and will stimulate further research of regulating the collapse.