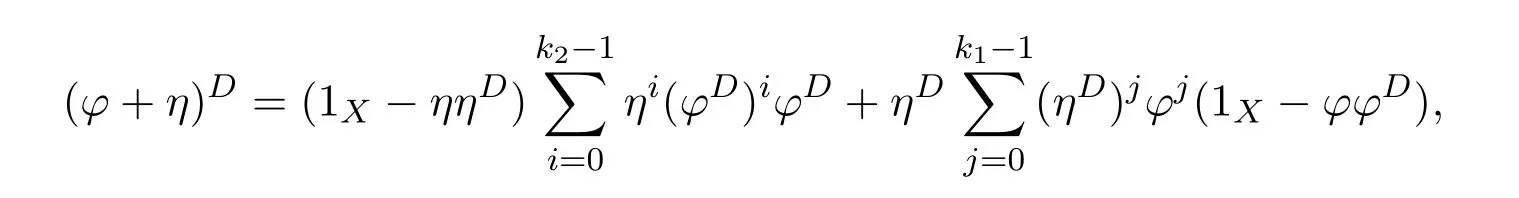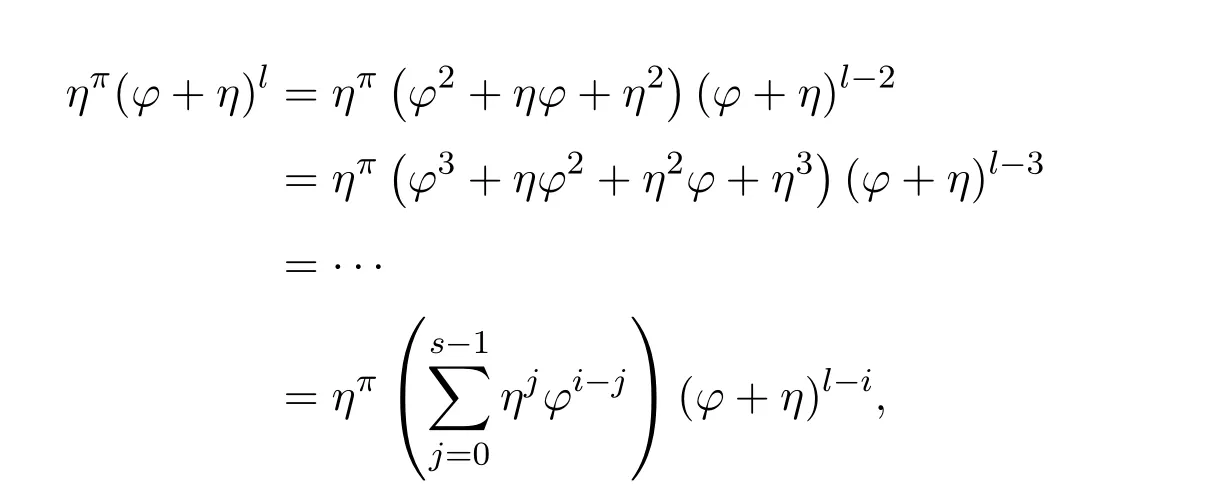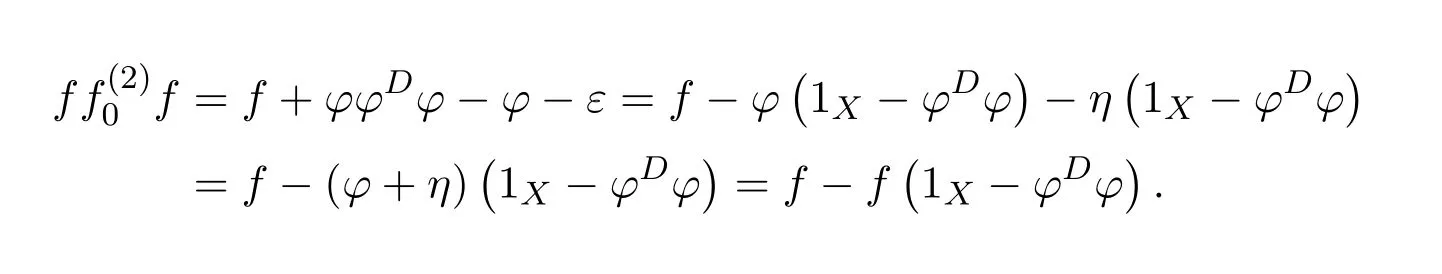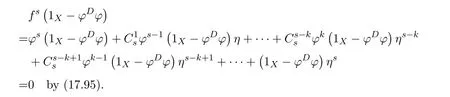ALGEBRAIC THEORY OF GENERALIZED INVERSES:GROUP INVERSES AND DRAZIN INVERSES*
Chen Jianlong
(School of Mathematics,Southeast University,Nanjing 210096)
Abstract This is the second part of a series of Algebraic Theory of Generalized Inverses,which includes two chapters:Group Inverses and Drazin Inverses.The chapter Group Inverses(see our Sec.1-9)first gives several sufficient and necessary conditions which guarantee the existence of the group inverse of a complex matrix,and then investigates the characterizations of group inverses in semigroups or rings;group invertibility of product paq,a sum of morphisms,the sum of two group invertible elements,a product,block matrices and a companion matrix.In the chapter Drazin Inverses(see our Sec.10-17),we give some calculation methods for Drazin inverses of complex matrices and study characterizations of Drazin inverses in semigroups or rings.Moreover,we also investigate Drazin invertibility of the product and difference of idempotents,matrices over a ring and a sum of morphisms.Among others,additive properties and Jacobson’s Lemma for Drazin inverses are presented.
Keywords ring,semigroup,group inverse,Drazin inverse.
1 The Group Inverse of a Complex Matrix
In this section,the group inverse of a complex matrix is introduced.Then we give several sufficient and necessary conditions which guarantee the existence of the group inverse of a complex matrix.
Definition 1.1LetA∈Cn×n.If there existsX∈Cn×nsuch that

thenXis called the group inverse ofA.If such anXexists,it is unique by Proposition 1.2 below and denoted byA#.
Proposition 1.2LetA∈Cn×n.IfAis group invertible,then the group inverse ofAis unique.
ProofIfX,Yare two group inverses ofA,then

Proposition 1.3([2,pp.156,Theorem2])LetA∈Cn×n.Then the following statements are equivalent:
(1)Ais group invertible.
(2)rank(A)=rank(A2).
(3)R(A)=R(A2).
(4)N(A)=N(A2).
Proof(1)(2).SinceAis group invertible,A2A#=A.Then rank(A)≤rank(A2).Therefore rank(A)=rank(A2).
(2)(1).Since rank(A)=rank(A2),there existY1andY2such thatA=A2Y1=Y2A2.It is easy to verify thatX==is the group inverse ofA.
(2)(3).It is obvious thatR(A2)(A).Since rank(A)=rank(A2),we haveR(A)∈R(A2).So,R(A)=R(A2).
(3)(2).BecauseR(A)=R(A2),rank(A)=rank(A2).
(3)(4).It is obvious.
Theorem 1.4([16,Theorem1])LetA∈Cn×nandA=GHbe a full rank decomposition.ThenAis group invertible if and only ifH Gis invertible.In this case,A#=G(H G)−2H.
ProofSupposeAis group invertible.By Proposition 1.3,we know that rank(A)=rank(A2),which implies rank(H G)=rank(A).ThereforeH Gis invertible.
Conversely,supposeH Gis invertible.It is easy to verify thatA#=G(H G)−2H.
Theorem 1.5 LetA=whereDis invertible andNis nilpotent.ThenAis group invertible if and only ifN=0.In this case,A#=.
ProofSupposeAis group invertible.By Proposition 1.3,we know that rank(A)=rank(A2),which follows that rank(N)=rank(N2).SinceNis nilpotent,N=0.
Conversely,supposeN=0.It is easy to verify that

2 Characterizations of Group Inverses in Semigroups or Rings
In this section,we firstly recall the definition of the group inverse in semigroups or rings.Then several sufficient and necessary conditions which guarantee the existence of the group inverse of an element are presented.Unless otherwise stated,Sdenotes a semigroup with identity andRdenotes a ring with identity.
Definition 2.1Leta∈S.If there existsx∈Ssuch that

thenxis called the group inverse ofa.If such anxexists,then it is unique(the proof is similar to that of Proposition 1.2)and denoted bya#.
Theorem 2.2([1,Lemma1])Leta∈S.Thenais group invertible if and only ifa∈a2S∩S a2.In this case,a#=y ax=y2a=ax2wherea=a2x=y a2.
ProofSupposea=a2x=ya2.By computation,we haveyax=ya2x2=ax2=y2a.Taket=yax=y2a=ax2.Then

Proposition 2.3([21,Proposition7])Leta∈R,thena∈R#if and only ifR=aR⊕a◦if and only ifR=Ra⊕◦a.
In this case,

where 1=ax+u=y a+vfor somex,y∈R,u∈a◦andv∈◦a.
ProofWe shall prove thata∈R#if and only ifR=aR⊕a◦.Supposeais group invertible.It is easy to verify thatR=aa#R⊕(1−aa#)R.Sinceaa#R=aRanda◦=(1−aa#)R,we haveR=aR⊕a◦.Conversely,ifR=aR⊕a◦,then there exists an idempotentesuch thataR=eRanda◦=(1−e)R.Therefore,ais regular,aR=eRandRa=Re.There existx1andx2such thate=ax1=x2a.So,x2a2=a2x1=a.By Theorem 2.2,we can easily complete the rest proof.
Theorem 2.4([44,Theorem2.7])Leta,x∈R.Then the following statements are equivalent:
(1)ais group invertible anda#=x.
(2)axa=a,xR=aRandRx=Ra.
(3)axa=a,◦x=◦aandx◦=a◦.
(4)axa=a,and.
(5)axa=a,◦x◦aandx◦a◦.
Proof(1)(2).We havea=axa=aax=xaaandx=xax=xxa=axx,soxR=aRandRx=Ra.
(2)(3)(4)(5).They are obvious by[11,Lemma 2.21].
(5)(1).Fromaxa=ait follows thatax−1∈◦a◦xand 1−xa∈a◦x◦so(ax−1)x=0 andx(1−xa)=0.Now,x=ax2=x2a,henceax=ax2a=xaandxax=x2a=x.By the uniqueness of the group inverse,x=a#.
The following theorem shows that the existence of the group inverse is closely related to existence of some idempotents.
Theorem 2.5([5,Proposition8.24])Leta∈R.Thenais group invertible if and only if there exists an idempotentesuch thatae=ea=0 anda+e∈R−1.In this case,a#=(a+e)−2a.
ProofSupposeais group invertible.Takee=1−aa#.Thenae=ea=0 and(a+e)−1=e+a#.
Conversely,if there exists an idempotentesuch thatae=ea=0 anda+e∈R−1,then(e+a)a=a2=a(e+a).Sincea+e∈R−1,we havea=(a+e)−1a2=a2(a+e)−1.By Theorem 2.2,we have thatais group invertible anda#=(a+e)−2a.
Theorem 2.6([44,Theorem2.11])Leta∈R.Then the following statements are equivalent:
(1)ais group invertible.
(2)there exists an idempotentqsuch thatq R=aRandRa=Rq.
(3)ais regular and there exists an idempotentqsuch that◦a=◦qanda◦=q◦.
If the previous statements are valid,then the statements(2)and(3)deal with the same unique idempotentq.Moreover,q a−qis invariant under the choice ofa−∈a{1}anda#=q a−q.
Proof(1)(2).Suppose thatais group invertible and setq=aa#=a#a.Thena=q a=aq,soq R=aR,Rq=Ra.
(2)(3).Fromq R=aRwe haveq=axanda=qzfor somex,z∈R.Therefore,q a=q2z=q z=aandaxa=q a=a,soais regular.The rest of the proof follows by[11,Lemma 2.21].
(3)(1).Suppose thatais regular and there exists an idempotentqsuch thata◦=q◦and◦a=◦q.Leta−∈a{1}be arbitrary.Since 1−a−a∈a◦q◦,we obtainq=q a−a.Also,1−q∈q◦a◦,soa=aq.Similarly,q=aa−qanda=qa.Setx=qa−q.We havex=a#,because

Now the invariance ofq a−qunder the choice ofa−∈a{1}follows.The uniqueness ofqfollows by[11,Lemma 2.16].
Chen et al.[13]present an existence criterion of the group inverse of a regular element.
Theorem 2.7([13,Proposition4.1])Letkbe an positive integer and suppose thatais regular with an inner inversea−.Then the following statements are equivalent:
(1)ais group invertible.
(2)u=ak+1−aa−∈R−1.
(3)v=ak+1−a−a∈R−1.
In this case,a#=u−1a2k−1v−1.
Proof(1)(2).Since

it follows thatuis right invertible.Similarly,we can prove that

Hence,u=ak+1−aa−∈R−1.
(2)(3).Note thatu=1+a(ak−1−a−)∈R−1if and only if 1+(ak−1−a−)a=v∈R−1by Jacobson’s Lemma.
(3)(1).Asv∈R−1,thenu∈R−1.Sinceua=ak+1=av,it follows thata=ak+1v−1=u−1ak+1∈a2R∩Ra2.Therefore,a∈R#by Theorem 2.2.
Note thata=u−1ak−1a2=a2ak−1v−1∈a2R∩Ra2.It follows from Theorem 2.2 thata#=u−1ak−1aak−1v−1=u−1a2k−1v−1.
Corollary 2.8([5,Proposition8.23])Ifa∈Ris regular with an inner inversea−,then the following conditions are equivalent:
(1)a∈R#.
(2)u=a2a−+1−aa−∈R−1.
(3)v=a−a2+1−a−a∈R−1.
(4)u′=a+1−aa−∈R−1.
(5)v′=a+1−a−a∈R−1.
In this case,

ProofIt is obvious by Jacobson’s Lemma and Theorem 2.7.
3 The Group Inverse of Product paq
Supposeais a regular element ofR.Our aim is to give necessary and sufficient conditions for the productt=paqto possess a group inverse.To do this we introduce the two elements

We may now state:
Theorem 3.1([43,Theorem1])Supposea∈Ris regular with an inner inversea−,u=aq paa−+1−aa−,v=a−aq pa+1−a−aandt=paq.Then the following are equivalent:

If in additionRa=Rpa,then these are also equivalent to

ProofWe first note that ifais regular thenaa−R=aR.
(i)(ii).uR=Rimplies thataq paR=aa−(aq paa−+1−aa−)R=aa−uR=aa−R=aR.
Conversely,ifaq pax=a,letα=axa−+1−aa−.Then
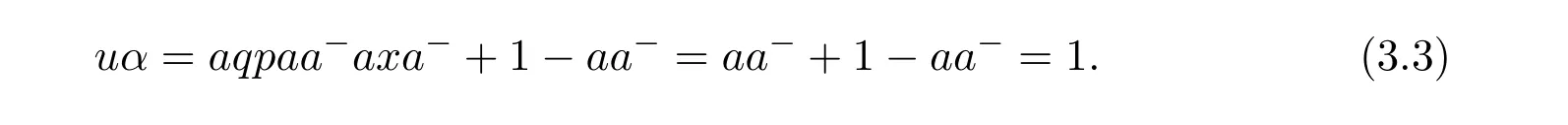
(ii)(iii).Ifaq pax=a,letβ=a−ax+1−a−a,then

Conversely,ifv R=Rthenaq paR=av R=aR.
(ii)(iv).Clearly(ii)implies thataR=aq R.HencetR=paq R=paR=paq paR=(paq)(paq)R=t2R.
Conversely,sinceaq R=aR,we have that(paq)(paq)R=paq Rimpliespaq paR=paR.Now by(iv)there existsp′such thata=p′pa.Therefore,pre-multiplication byp′yieldsaq paR=(p′pa)q paR=p′paR=aR.
Remark 3.2([43,pp.141,Remarks])
(1)By symmetry it follows that the following are equivalent:

If in additionaR=aq Rthen these are also equivalent to

(2)Ifpandqare invertible then the following are equivalent:

and

Combining(3.2)and(3.5),we have
Corollary 3.3([43,Corollary1])The following are equivalent:
(1)uis a unit.
(2)Raq pa=Ra,aq paR=aR.
(3)vis a unit.
(4)t#exists andaR=aq R,Ra=R pa.
Moreover

where

andaq pax=a=yaq pa.

ProofTo computet#we note first thatua=aq pa=avand thus anda=u−1(aq pa)=(aq pa)v−1.Hencepaq=pu−1aq paq=pu−1p′(paq)(paq)ort=ht2,whereh=pu−1p′.Likewise,t2g=t,whereg=q′v−1q.
From[22]we may conclude thatt#=htg=pu−1p′paq q′v−1qwhich shows that

By(3.7)we also have the asymmetric forms

The expressions foru−1andv−1follow from(3.3)and(3.4).
Corollary 3.4([43,Corollary2])Ifpandqare invertible then the following are equivalent:
(1)uis a unit.
(2)Raq pa=Ra,aq paR=aR.
(3)vis a unit.
(4)t#exists.We may also setaq=s,pa=randt=r a−s.In addition,we could takep=r a−andq=a−s.We then have the following theorem.
Theorem 3.5([43,Theorem2])Supposeais regular with an inner inversea−,aR=sR,Ra=Rrand

Then the following are equivalent:

and

In which case,

4 The Group Inverse of a Sum of Morphisms
In this section,the group inverse of a sum of morphisms is investigated.
Proposition 4.1([49,Proposition1])LetCbe an additive category.Suppose thatϕ:X−→Xis a morphism ofCwith group inverseϕ#and thatη:X−→Xis a morphism ofCsuch that 1X+ϕ#ηis invertible.Let

and

Then the following conditions are equivalent:
(1)f=ϕ+η−εhas a group inverse.
(2)1X−γand 1X−δare invertible.
(3)1X−γis left invertible and 1X−δis right invertible.
In that case

and

ProofBy[11,Lemma 14.1],(1X+ϕ#η)−1ϕ#∈f{1,2}.Let

Then

andfϕ#=β−1ϕϕ#.So=fαϕ#=fϕ#β=β−1ϕϕ#βand


and

We have

(which impliesfγ=0),

and

Now we are ready to show the equivalence of three conditions.
(1)(2).First,we show that 1X−ϕ#ϕ+f#fϕ#ϕis a right inverse of 1X−γ.Note that

Multiplying the equality byϕ#ϕon the right,we obtain(1X−γ)f f#ϕ#ϕ=ϕ#ϕ.Since

we obtain

Next,we show that this right inverse is also a left inverse for 1X−γ.Note first that

So,(1X−ϕ#ϕ)γ=(1X−ϕ#ϕ)ηϕ#β=(1X−ϕ#ϕ)(1X−β)and

On the other hand,
Therefore,

Hence 1X−γis invertible and(1X−γ)−1=1X−ϕ#ϕ+f#fϕ#ϕ.Similarly,we have that 1X−δis invertible,and(1X−δ)−1=1X−ϕϕ#+ϕϕ#f f#.
(2)(3).Obvious.
(3)(1).Letωdenote the left inverse of 1X−γandtthe right inverse of 1X−δ.Sincef(1X−δ)=and(1X−γ)f=,we have

This means that the equationsf=f2xandf=y f2have solutionsx0=andy0=,respectively.Therefore,the group inversef#offexists andf#=y0f x0=by Theorem 2.2.
From(1)(2),we know that 1X−γand 1X−δare invertible andω=(1X−γ)−1,t=(1X−δ)−1.Sof#=(1X−γ)−1αϕ#(1X−δ)−1.
Remark 4.2([49,Remark1])The method for proving(3)(1)belongs to Hartwig(see[23]).
Corollary 4.3([28,Proposition3])Ifa∈Rhas a group inversea#andj∈J(R),thena+jhas a group inverse if and only if(1−aa#)j(1+a#j)−1(1−a#a)=0.
In that case,(a+j)#=(1−γ)−1(1+a#j)−1a#(1−δ)−1,in which

ProofSincej∈J(R),the element 1+a#jis invertible.
“”.By hypothesis,ε=0,sof=a+j.Since 1−γand 1−δare invertible,a+jhas a group inverse by Proposition 4.1.In that case,(a+j)#=(1−γ)−1(1+a#j)−1a#(1−δ)−1.
“”.Letτ=(a+j)#.By[11,Lemma 14.1],τ∈ε{1},i.e.,ετε=εandε(1−τε)=0.Sinceε=(1−aa#)j(1+a#j)−1(1−a#a)∈J(R),1−τεis invertible andε=0.
5 The Group Inverse of the Sum of Two Group Invertible Elements
In this section,we assume thatRis a Dedekind-finite ring.The group inverses of sum and difference of two group invertible elements are presented under different conditions.
Theorem 5.1([52,Theorem3.1])Leta,b∈R#and 2∈R−1.Ifabb#=baa#,then
(1)a+b∈R#and(a+b)#=a#+b#.
(2)a−b∈R#and(a−b)#=a#−b#−ba#a#+ab#b#.
ProofSinceabb#=baa#,we haveabb#(b#aa#)abb#=ab#abb#=ab#baa#=abb#.Sob#aa#is an inner inverse ofabb#.Then we have

SinceRis a Dedekind-finite ring,(1+abb#−b#abb#)(1+b#aa#−b#abb#)=1.From Theorem 2.7,we know thatabb#∈R#.Sinceb#(baa#)2=b#babb#=b#bbaa#=baa#,we have

Similarly,(baa#)#=a#bb#.Soa#bb#=b#aa#.Furthermore,aa#bb#=ab#aa#=abb#b#aa#=b#aa#abb#=b#abb#=b#baa#.In addition,

Similarly,aa#ba#=ba#andaa#b#a=b#a.We know thatabaa#=abb#baa#=baa#abb#=babb#=bbaa#.Henceaba#=bba#.Sincea#b#aa#=a#bb#b#aa#=b#aa#a#bb#=b#a#bb#=b#b#aa#,a#b#a=b#b#a.Similarly,we can getbab#=aab#andb#a#b=a#a#b.From the above discussion,we have

(1)Letx=a#+b#.By equalities(5.10)-(5.12),
then

and
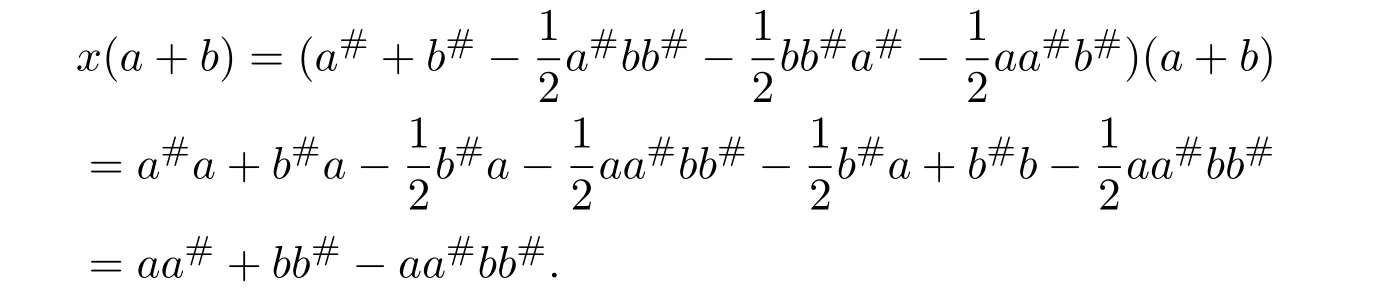
So(a+b)x=x(a+b).By equalities(5.10)and(5.11),we have

and

and
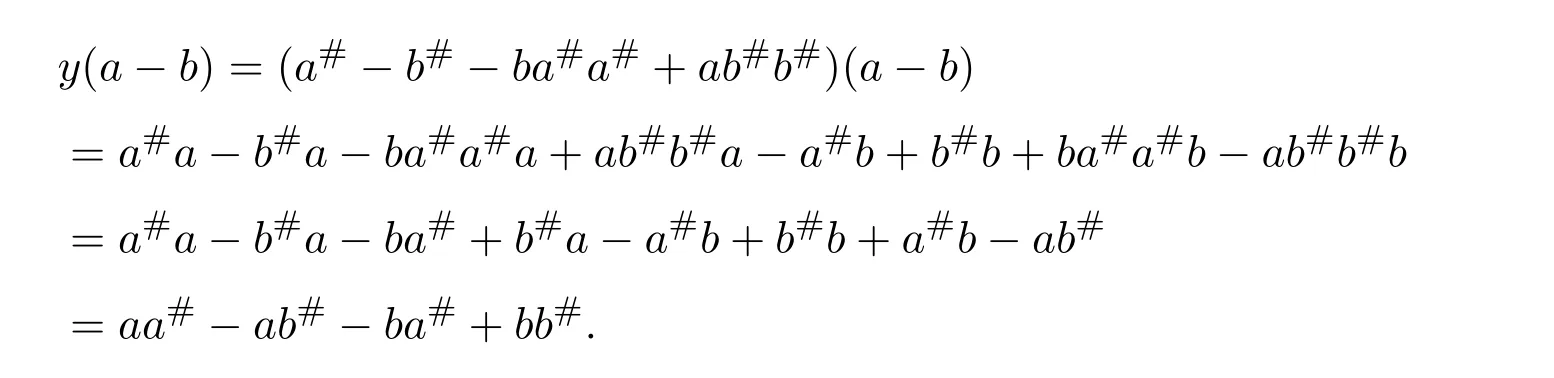
So(a−b)y=y(a−b).By equalities(5.11)and(5.15),we have

Thus,

Since

we have
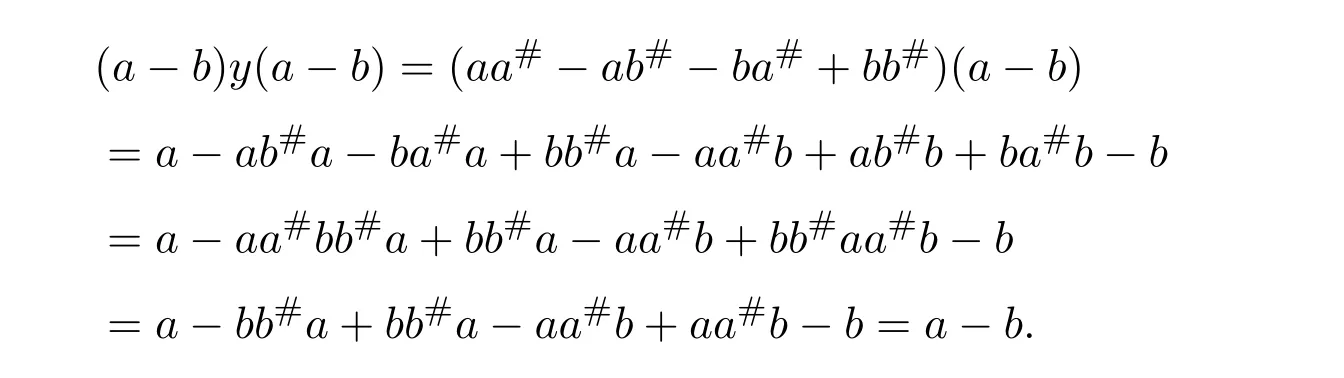
Therefore,(a−b)#=a#−b#−ba#a#+ab#b#.
Next,we present the expressions of(a+b)#and(a−b)#under the conditionbb#a=aa#b.
Theorem 5.2([52,Theorem3.2])Leta,b∈R#and 2∈R−1.Ifbb#a=aa#b,then
(1)a+b∈R#and(a+b)#=a#+b#.
(2)a−b∈R#and(a−b)#=a#−b#−a#a#b+b#b#a.
ProofSincebb#a(aa#b#)bb#a=bb#ab#a=aa#bb#a=bb#a,aa#b#is an inner inverse ofbb#a.Sincebb#a=aa#b,we have

SinceRis a Dedekind-finite ring,(1+aa#b#−bb#ab#)(1+bb#a−bb#ab#)=1.So 1+bb#a−bb#ab#∈R−1.From Theorem 2.7,we know thatbb#a∈R#.Sincebb#aa#a=bb#a=aa#b,(bb#a)#aa#=aa#b#.Then we have

Hence(bb#a)#=aa#b#.Similarly,(aa#b)#=bb#a#.Therefore,bb#a#=aa#b#.We have

In addition,
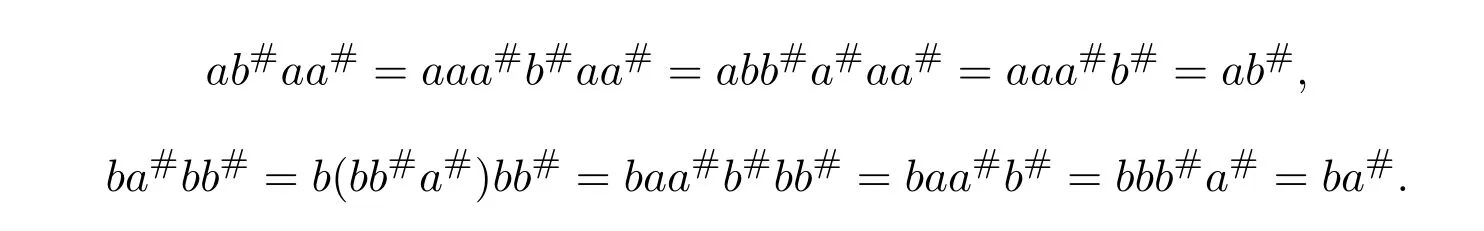
Sincebb#ab=bb#aaa#b=aa#bbb#a=aa#ba=bb#aa,b#ab=b#aa.Similarly,a#ba=a#bb.Sincebb#a#b#=bb#a#aa#b#=aa#b#bb#a#=aa#b#a#=bb#a#a#,ba#b#=ba#a#.Hence,b#a#b#=b#a#a#.Similarly,ab#a#=ab#b#anda#b#a#=a#b#b#.To sum up,we have the following equalities:

(1)Letx=a#+b#−.By equalities(5.16),(5.18),and(5.19),we obtain that

and

So(a+b)x=x(a+b).By equalities(5.16)and(5.18),we have

and

(2)Lety=a#−b#−a#a#b+b#b#a.By equalities(5.19)-(5.21),then

and

Hence,(a−b)y=y(a−b).Sincea#b#a=a#aa#b#a=a#bb#a#a,by equalities(5.16),(5.17),(5.18)and(5.20),we obtain
By equalities(5.16)and(5.21),we have
Thus(a−b)#=a#−b#−a#a#b+b#b#a.
According to the above two theorems,we have the following corollary.
Corollary 5.3([52,Corollary3.3])Leta,b∈R#and 2∈R−1.Ifabb#=baa#andbb#a=aa#b,then
(1)a+b∈R#and(a+b)#=a#+b#−.
(2)a−b∈R#and(a−b)#=a#−b#.
ProofBy the proof of the above two theorems,we have

From Theorem 5.1,we obtain

and

6 The Group Inverse of a Product
Mary and Patr´ıcio[34]characterized the existence of the group inverse of a product of two regular elements by an unit and gave the corresponding expression.Leta,bbe regular elements inR,with reflexive inversesa+,b+,respectively.Let also which we will assume to be regular inR.Note that the regularity ofwdoes not depend on the choices ofa+andb+.That is to say,ifwis regular for a particular choice ofa+and ofb+,then it must be regular for all choices ofa+andb+.This can be easily proved by noting thatwbeing regular is equivalent to the regularity of the matrix,using[38],which in turn is equivalent to(1−bb=)(1−a=a)being regular,for any other choices of inner inversesa=andb=ofaandb.Consider the matrixAQwithA=.It is well known thatM#exists if and only if(ab)#exists,using[25].Furthermore,the(1,1)entry ofM#equals(ab)#.Also,M#exists if and only ifU=AQ+I−AA−is invertible,see[43,37],in which case(AQ)#=U−2(AQ).
AsAQ+I−AA−=A(Q−A−)+IthenAQ+I−AA−is invertible if and only if(Q−A−)A+I=QA+I−A−Ais invertible,using Jacobson’s Lemma,which in turn means(QA)#exists.Therefore,by considering the matrixW=QA=then(ab)#exists if and only ifWis group invertible.Using[36],the matrixWis group invertible if and only if

is a unit.We have,hence,the equivalence(ab)#exists if and only if 1−a+a+ba+(1−ww−)(1−bb+)is a unit.Using the expression presented in[36]does not give a tractable algorithm to actually compute(ab)#.We will,therefore,pursue a different strategy and compute the(1,1)entry ofM#.Recall that forM=AQandQinvertible,the group inverse ofMexists if and only ifU=AQ+I−AA−is invertible.For,there existsA−for which

by using[38].The matrixUthen becomes

Multiplication on the right byK=gives

where

as(1−bb+)b=0.We are left with showing when isGinvertible.We do so using the Schur complement on the(1,1)entry.This Schur complement equals

This gives,and as previously shown,(ab)#exists if and only ifz=1−a+a+ba+(1−ww−)(1−bb+)is a unit.
As a side note,we construct another unit associated withz,namely we may show thatz=1−a+a+ba+(1−ww−)(1−bb+)is a unit if and only ifz′=1−aa++ab−a(1−ww−)(1−bb+)a+is a unit.This follows by the sequence of identities(1−ww−)(1−bb+)=(1−ww−)(1−bb+)(1−a+a+a+a)=(1−ww−)(1−bb+)a+atogether with Jacobson’s Lemma.
We remark that given a reflexive inversew+ofw,the element˜w=(1−a+a)w+(1−bb+)is an idempotent reflexive inverse ofw.As suchzandz′simplify to 1−a+a+ba+1−bb+−w˜wand 1+ab−abb+a+−aw˜wa+,respectively.
We know,using[37,Corollary 3.3(4)],that(AQ)#exists if and only ifUis invertible,in which case(AQ)#=U−2(AQ).The matricesUandGare equivalent,and we are able to relate their inverses by means of the matrixK.Indeed,sinceG=U K,thenU−1=K G−1.Firstly,we need to compute the inverse ofG,for which we will use the following known result:
Lemma 6.1Letx,y,z∈R.Thenis invertible if and only ifz−xyis invertible.In this case

whereζ=z−xyis the Schur complement.
Our purpose is to derive an expression for(ab)#,which equals the(1,1)entry ofM#.The(1,1)entry ofM#is obtained by multiplying the first row ofU−2by the first column ofAQ,which is.So,in fact we just need the(1,1)entry ofU−2,which is then multiplied on the right byabto give(ab)#.
We recall thatG=U K,where,which givesU−1=K G−1andU−2=K G−1K G−1.Pre-multiplication withKdoes not affect the first row,and so we just need the(1,1)element ofG−1K G−1.Calculations show that

We will need the simplification

from which we obtain

Indeed,αab=aa+ab−bab+2(1−ww−)(1−bb+)a+abwhose last summand can be expressed as

and thereforeαab=a+ab−bab.Therefore,

from which we obtain the general formula

From 1−a+a=z−1−z−1a+awe obtain,by post-multiplying byb,

which implies

Now,from(6.22)we havez−1b=b+z−1a+ab−z−1babwhich implies,using(6.23),that

which in turns delivers

Using(6.25)and(6.26),together with(ab)#=2az−1b−2(az−1b)2+az−2b,we write the idempotent(ab)#(ab)as

Using(6.24),this equals toaz−1band thereforeaz−1bis an idempotent,the unit of the group generated byab.This simplifies the expression of(ab)#to

It comes with no surprise that the expression of(ab)#is of the formaX b,for a suitableX.We have,from the above,our main result:
Theorem 6.2([34,Theorem2.2])Leta,bbe regular elements inRwith reflexive inversesa+andb+,respectively.Assume,also,thatw=(1−bb+)(1−a+a)is regular.Then(ab)#exists if and only ifz=1−a+a+ba+(1−ww−)(1−bb+)is a unit.In this case,

7 The Group Inverse of Block Matrices
In this section,we introduce group inverses of block matrices.At first,we introduce two useful lemmas.
Lemma 7.1([9,Lemma1.1])Leta∈Rbe regular,b∈R,and assume that there exists a reflexive inversea+such thata+b=ba+=0.Ifa+bis regular thenbis regular andb−=(a+b)−is an inner inverse ofb,for any(a+b)−.
Lemma 7.2([9,Lemma1.2])LetP,Q,A∈R2×2.IfM=P AQwherePandQare units andAis regular,then the group inverse ofMexists if and only ifS=AQP+I−AA−is a unit ofR2×2,independent of the choice ofA−,or equivalently,T=QP A+I−A−Ais a unit,in which case

ProofIt is obvious by Corollary 3.3.
From now on we assume thatd∈Ris regular and thatd+is a fixed but arbitrary reflexive inverse ofd.Let us introduce the notation

With this notation,we have the following decomposition of the matrixM∈R2×2

In the notation of(7.27),we assume bothebandcfto be regular elements inR.Set

for fixed but arbitrary(eb)+and(cf)+.
Lemma 7.3([9,Lemma2.1])Lete,f,s,p,qandwbe as in(7.27)and(7.29).We have thatis regular inR2×2if and only ifwis regular inR.In this case,

is an inner inverse ofAand

ProofLet us first observe that the following relations hold:

Now,consider

Hence,Ais regular if and only ifis regular.Usingw=qsp,we can write

Conversely,assume thatwis regular.LetWe claim thatXis an inner inverse ofIndeed,

In view of(7.32)we conclude that an inner inverse ofAis given by(7.30)and,thus,Ais regular.It remains to prove(7.31),but the proof of this is straightforward.
We can now formulate our main result.It is required thatdhas the group inverse.Accordingly,we can setd+=d#.In this case,in the notation of(7.27)we havee=1−dd#=1−d#d=f.It follows thatde=ed#=0.Moreoverd+eis a unit ofRand(d+e)−1=d#+e.
Theorem 7.4([9,Theorem2.2])Letdbe group invertible.With the notation(7.27)and under the assumptions of(7.29),withd+replaced byd#,ifwis regular inRthen the group inverse of the matrixexists if and only if

is a unit ofR.In this case,,where

with

ProofWriteM=P AQas in(7.28).By Lemma 7.2,the group inverse ofMexists if and only ifS=AQP+I−AA−is a unit,independent of the choice ofA−.For
the inner inverse provided in Lemma 7.3,we have

Now,let us introduce the matrixF=.We have

where

Since[d#b(eb)+e]2=0,it follows that 1+d#b(eb)+eis a unit ofR.Moreover,d+eis a unit becausedhas group inverse.Thus,his a unit and

On account that the(2,2)entry of the matrixS Fis a unit,it follows thatS Fis a unit ofR2×2if and only if the Schur complement is a unit ofR.Therefore,the matrixSis a unit if and only if

is a unit ofR.From(7.38)we getgb=eb+d#bp.Further,using the last relation of(7.37)we obtain

By substituting this expression in(7.39)we conclude thatuhas the form given in(7.33).
By Lemma 7.2,M#=P S−2AQ.From(7.36)it follows that

Next,we compute

the last equality is due to the fact thateg=e. In the sequel,we denoteα=u−1(1−ww−)qandβ=αcd#+u−1ce.From(7.38),(7.37)and(7.39)it follows that

respectively.In deriving the last equality we have multiplied on the left expression(7.39)byu−1.Then

Using(7.40)and(7.42)we obtain

where

From(7.38)it follows thatg2b=g b−d#(b−d#bp).Using this latter expression and(7.41)we get

By substituting this into(7.43),usingu−1xd#=−αc(d#)2,and regrouping terms we get(7.34).
Next,some applications are indicated.We begin with the case thatdis a unit ofR.
Corollary 7.5([9,Corollary3.1])LetM=,wheredis a unit ofR,and lets=a−cd−1bbe regular.Then the group inverse ofMexists if and only if

is a unit ofR.In this case,,where

with

In addition,letsbe group invertible.Denotet=1−ss#.Then the following statements are equivalent:
(1)M#exists.
(2)u=s+t(1+tcd−2b)is a unit ofR.
(3)1+tcd−2bis a unit ofR.
(4)d2+btcis a unit ofR.
ProofNote thatdis a unit,we havee=1−dd#=0 and sop=q=1.Thusw=s.The rest of the proof follows from Theorem 7.4.
The next corollary provides a compact representation for the group inverse ofM.
Corollary 7.6([9,Corollary3.2])LetM=,whereb,cand

are regular elements inR.Then the group inverse ofMexists if and only if

is a unit ofR.In this case,,where

withα=u−1(1−ww−)(1−cc+)andδ=α+u−1(a+1−b+b).
ProofThis result follows from Theorem 7.4 since,in this case,d=0 and soe=1,s=a,p=1−b+b,q=1−cc+andw=(1−cc+)a(1−b+b).
8 The Group Inverse of a Companion Matrix
One of the fundamental building block in the theory and applications of matrices,is the lower companion matrix associated with a monic polynomialf(x)=p0+p1x+···+pn−1xn−1+xn.It is defined by

and is the simplest example of ann×nnon-derogatory matrix.Throughout this sectionnwill be fixed.
It was shown in[25]that over a ring,L#withn≥2,exists exactly when there exist solutionsxandyin the ringR,such that(i)

(ii)

(iii)

In which caseL#has the form


The casen=2 is included in this if we setp2=1,y2=yand dropIn−2from(8.48).This gives

Consider then×ncompanion matrixoverR,wherea=a0andk=[a1,a2,...,an−1]T.
Theorem 8.1([43,Theorem3])The following are equivalent:
(1)The group inverseL#ofLexists.
(2)ais regular andh=a−(1−aa−)a1is invertible.
(3)ais regular andk=a−a1(1−a−a)is invertible.
ProofFor convenience,we seta1=banda2=c.Consider the companion matrixLand its factorization

BecausePandQare invertible,it is necessary in order forL#to exist,thatAand henceabe regular.Let us now assume thatais a regular and apply Corollary 3.4 to simplify the conditions forL#to exist,and then use(3.6)to compute the actual group inverse.From(8.48)we recall that it suffices to computeandIn order to construct the matricesUandV,we must consider


in whiche=1−aa−.Similarly

wheref=1−a−a.Next we define

ThenU=F W1andV=F W2,whereWi=W(Xi)and

We note that ifn=2,thenU=X1andV=X2.As such let us first turn to the case wheren>2.We shall need the following facts:

Using these identities we see that

and

Let us now apply these to the three formulae forL#.
Case(I)L#=PU−2AQ.Now

From(8.53)we thus see that forn>2,

Likewise

Case(II)L#=P AV−2Q.Now

which gives

Likewise

Case(III)L#=P U−1AV−1Q.
In this case,

and

Thus equating the three cases we arrive forn>2 at the identities

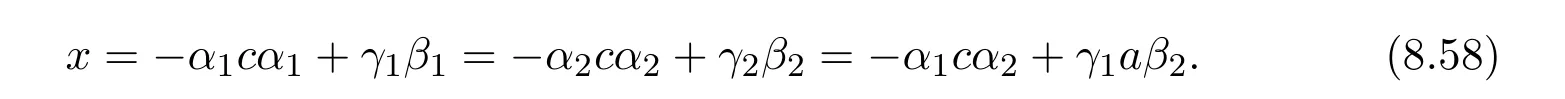
This shows that we must have

In order to verify these we need the explicit expressions for.This we now pursue.
From(8.51)we may factor theXias

whereh=a−eb,and by symmetry

wherek=a−bf.
This shows thatUandVare invertible inRn×nwithn≥2,exactly whenh=a−ebandk=a−bfare respectively invertible inR.Again this is independent of the choice ofa−.Inverting theXiwe see that

Likewise

Thus

Let us now check these identities.Firsthf=−ebf=ek,and thus

which ensures thatα1=α2.Next,we observe thatf k−1a=h−1ea=0,and hence

which says that

The remaining identity follows by symmetry,i.e.,γ1αβ2=γ1β1.In conclusion,let us compute the actual expression forL#.
Theorem 8.2([43,Theorem4])SupposeL=with.Define the constants

IfL#exists then the constantsxandyfrom(8.48)are given by

ProofAll that remains is to prove the case wheren=2.In this case,we again only need computexandyafter which we setx1=y−bxandy1=1−by.It follows from(8.49)-(8.50)thatU=X1andV=X2.Moreover the values ofandchange to

This gives

Likewise

completing the proof.
9 EP Elements
Recall thatA∈Cn×nis called EP[45]ifR(A)=R(A*).In this case,A=whereUis a unitary matrix andDis invertible or zero.Hartwig[21]introduced EP elements in rings with involution.Throughout this section,Ris a*-ring.
Definition 9.1Leta∈Rbe Moore-Penrose invertible and group invertible.Ifa†=a#,thenais called an EP element.
Proposition 9.2([21,Proposition25])Leta∈R.Then the following statements are equivalent:
(1)ais EP.
(2)a†exists andaa†=a†a.
(3)(3)a#exists and(aa#)*=aa#.
Proof(1)(2).Sinceais EP,we havea†=a#.Therefore,aa†=aa#=a#a=a†a.
(2)(3).Becauseaa†=a†a,ais group invertible anda#=a†.So,(aa#)*=(aa†)*=aa†=aa#.
(3)(1).Since(aa#)*=aa#andaa#=a#a,we have(a#a)*=a#a.Therefore,ais Moore-Penrose invertible anda†=a#.That is,ais EP.
The following theorem coincides with[39,Proposition 2].For convenience,we rewrite it as follows.
Theorem 9.3([39,Proposition2])Leta∈R.Then the following statements are equivalent:
(1)ais EP.
(2)a†exists andaR=a*R.
(3)a#exists andaR=a*R.
Proof(1)(2).By Proposition 9.2,we haveaa†=a†a,which impliesaa†R=a†aR.Sinceaa†a=aand(a†a)*=a†a,we haveaR=aa†Randa*R=a†aR.Therefore,aR=a*R.
(2)(3).Sinceaa†R=aR=a*R,aa†a*=a*which impliesa2a†=a.BecauseaR=a*R=a†aR,we havea†a2=a.From Theorem 2.2,a#exists.
(3)(1).Sincea#exists andaR=a*R,aa#R=aR=a*R=(aa#)*Rwhich implies(aa#)*=aa#(aa#)*.Therefore,aa#=(aa#)*.Thenais EP by Proposition 9.2.
By the above theorem,we can easily get the following corollary,which shows that the notion of an EP element inRis really the generalization of an EP matrix.
Corollary 9.4LetRbe a*-regular ring anda∈R.Thenais EP if and only ifaR=a*R.
The following theorem characterizes an EP element by units.
Theorem 9.5([39,Theorem4])Ifa∈Ris regular with an inner inversea−,then the following are equivalent and independent from the choice ofa−:
(1)ais EP.
(2)aa*aa−+1−aa−anda2aa−+1−aa−are invertible and

(3)a−aa*a+1−a−aanda−aa2+1−a−aare invertible and

Moreover,ifu=a2aa−+1−aa−,v=a−aa2+1−a−a,=aa*aa−+1−aa−and˜v=a−aa*a+1−a−athen

ProofFollows directly from the results in[35,43]if we can replacea2a−+1−aa−bya2aa−+1−aa−,and analogouslya−a2+1−a−abya−aa2+1−a−a.Indeed,a2a−+1−aa−is invertible if and only if

is invertible.Then

The remaining fact to prove is thata#=a†=a(a2)−a(a2)−a.Indeed,ifa#exists thena2is regular and

since

and

Therefore,

and
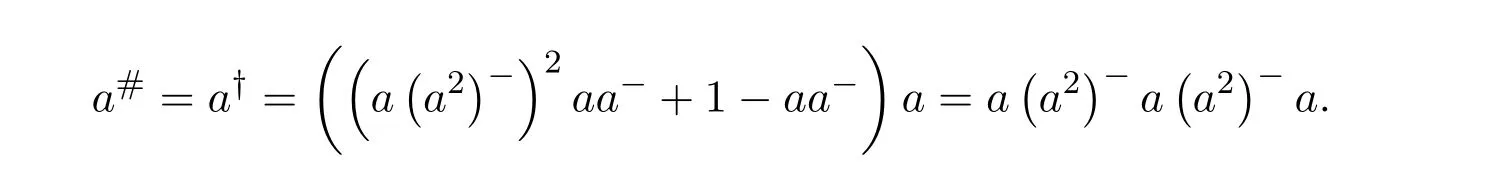
Remark 9.6([39,Remark])Supposea∈Ris regular with an inner inversea−.Thenais EP if and only if

and

for any choice ofa−,since

The following property can be considered as the generalization of a result of Katz,and of its extension to Dedekind-finite rings.Indeed,Katz proved,see[2,p.166,ex.18],that for any square complex matrixA,A†=A#if and only if there is a matrixYsuch thatA*=Y A.His result can be lifted up to the following:
Proposition 9.7([39,Fact5])LetRbe a Dedekind-finite ring anda†exists.Thena*=ya,for somey∈R,if and only ifais EP.
ProofIfa†exists,then also(a†)*exists and equals(a*)†.Sincea*=y athena=a*y*and hence.Moreover,aR∼=a*Rsinceφ:aR→a*R,withφ(ax)=a†ax,is aR-module isomorphism.Then,alsoaa†R∼=a†aR,which impliesaa†R=a†aR,oraR=a*Rby using[24,Theorem 1].By Theorem 9.3,a#exists anda†=a#.
Conversely,ifa#exists anda†=a#thena*=(aa†a)*=a*aa†=a*aa#=a*a#a.It suffices to takey=a*a#.
The following theorem shows that the equalityaR=a*Rin Theorem 9.3 can be replaced by the weaker inclusionsora*RaR.
Theorem 9.8([48,Theorem3.9])Leta∈R.Then the following statements are equivalent:
(1)ais EP.
(2)a∈R#and.
(3)a∈R#and.
Proof(1)(2).It is obvious by Theorem 9.3.
(2)(1).Bywe havea=a*rfor somer∈R,thena=(aa#a)*r=(a#a)*a*r=(a#a)*a.Thusa#a=aa#=(a#a)*aa#=(a#a)*a#a,which gives(a#a)*=a#a.Therefore,ais EP.
(1)(3).It is similar to the proof of(1)(2).
Recall that an infinite matrixMis said to be bi-finite if it is both row-finite and column-finite.
Example 9.9([48,Example4.6])LetRbe the ring of all bi-finite real matrices with transpose as involution and letei,jbe the matrix inRwith 1 in the(i,j)entry and 0 elsewhere.LetA=andB=A*,nowAB,B A=I.SoA†=BandA†=A†B A=B2A.It is easy to check thatB2is not left invertible andAis not EP(sinceAB/=B A).In addition,Ais not group invertible(ifA∈R#,thenAA#=A#A=B AA#A=B A=I;thus,Ais invertible,which is not possible.).This example also shows that the equalityaR=a*Rin the equivalence(ais EP=a*R)cannot be replaced by the inclusionsora*RaR.
Theorem 9.10([48,Theorem4.4])Leta∈R†.Then the following statements are equivalent:
(1)ais EP.
(2)There exists a unitu∈Rsuch thata†=ua.
(3)There exists a left invertible elementv∈Rsuch thata†=va.
Proof(1)(2).Ifais EP,thena∈R†anda†=a#.Letu=(a#)2+1−aa#.Sinceu(a2+1−aa#)=(a2+1−aa#)u=1 we get thatuis a unit.Furthermore,a=a#=a†.
(2)(3).It is clear.
(3)(1).Suppose that there exists a left invertible elementv∈Rsuch thata†=v a.Then 1=tvfor somet∈Randta†=tv a=a.ThusRa†RaandSinceRa†=Ra*,we deduce thatRa*=Ra,that isais an EP element.
In the following theorem,we show that an EP element in a ring can be described by three equations.
Theorem 9.11([48,Theorem2.2])Leta∈R.Thenais EP if and only if there existsx∈Rsuch that

ProofSupposeais EP.Letx=a†=a#.Then(xa)*=(a†a)*=a†a=xa xa2=a#a2=aandax2=a(a#)2=a#=x.Conversely,if there existsx∈Rsuch that(xa)*=xa,xa2=aandax2=x,thena(x2a)=(ax2)a=xa=x(xa2)=(x2a)a,a(x2a)a=(xa)a=xa2=a,and(x2a)a(x2a)=(xa)(x2a)=x(ax2)a=x2a.These three equalities prove thata∈R#,a#=x2a,andaa#=xa.By Proposition 9.2,we getais EP.
We will characterize whena∈Ris EP by another three equations.
Theorem 9.12([48,Theorem2.11])Leta∈R.Thenais EP if and only if there existsx∈Rsuch that

ProofIfais EP,by takingx=a†=a#,we get the above three equations.Conversely,assume that there existsx∈Rsuch that the above three equations are satisfied.We shall show thatais EP anda#=ax2.Sinceax=xa,we geta(ax2)=(ax2)a,but in addition,a(ax2)=(a2x)x=ax,which leads toa(ax2)a=a2x=aand(ax2)a(ax2)=(ax2)ax=(a2x)x2=ax2.Sinceaa#=a2x2=axis Hermitian,the conclusion follows from Proposition 9.2.
The following theorem gives an equivalent characterization of an EP element.
Theorem 9.13([3,Theorem2.1])Leta∈R.Then the following statements are equivalent:
(1)There exists a unique projectionpsuch thata+p∈R−1andap=pa=0.
(2)ais EP.
Proof(1)(2).Sinceap=0 andp2=p,we get(a+p)p=p.The invertibility ofa+pentailsp=(a+p)−1p,and in a similar way we getp=p(a+p)−1.Now,we claim

In fact:

This proves the claim.Analogously we can prove[(a+p)−1−p]a=1−p.Now,we are going to prove thata†=(a+p)−1−p.We have

and

Evidently[(a+p)−1−p]a=a[(a+p)−1−p]=1−pis self-adjoint.This proves thata†=(a+p)−1−p.Sinceaa†=1−p=a†a,we getais EP.
(2)(1).Letpbe the projection defined byp=1−aa†.Evidently,we haveap=pa=0.Now,pa†=pa†aa†=paa†a†=0,and similarlya†p=0 holds.Let us provea+p∈R−1.We have(a+p)(a†+p)=aa†+ap+pa†+p=aa†+p=1 and analogously we have also(a†+p)(a+p)=1.Now,we shall prove the uniqueness.Assume thatqis another projection such thataq=q a=0 anda+q∈R−1.The computations made in(1)(2)show thata†=(a+p)−1−p=(a+q)−1−q.Premultiplying byawe geta(a+p)−1=a(a+q)−1.Now,9.1 impliesa(a+p)−1=1−panda(a+q)−1=1−q.Therefore,1−p=1−qand the uniqueness is proved.
Recall thata∈Ris called*-strongly regular if there exist a projectionpandu∈R−1such thata=pu=up.The following theorem can be seen as an application of Theorem 9.13.
Theorem 9.14([26,Theorem3.3])Leta∈R.Then a is EP if and only if a is*-strongly regular.
ProofSuppose thataisE P.Then,by Theorem 9.13,there exists a unique projectionpsuch thata+p∈R−1andap=pa=0.Writea+p=u∈R−1.Thena=a(1−p)=u(1−p)=(1−p)u.Therefore,ais*-strongly regular.
Conversely,assume thatais*-strongly regular.Then there exist a projectionpandu∈R−1such thata=pu=up.Since(a+1−p)(u−1p+1−p)=(u−1p+1−p)(a+1−p)=1,a+1−p∈R−1.Sincea(1−p)=(1−p)a=0,it follows thatais EP by Theorem 9.13.
10 Drazin Inverses of Complex Matrices
In this section,we first introduce the Drazin inverse of a complex matrix and show its existence and uniqueness.Then we present a matrix decomposition related to the Drazin inverse.
Definition 10.1([2,Chapter4,pp.145])LetA∈Cn×n.ThenX∈Cn×nis called the Drazin inverse ofAif there exists a positive integerksuch that

We next see the existence and uniqueness of such anX.
Theorem 10.2([2,pp.145,Theorem7])LetA∈Cn×n.ThenAhas at most one Drazin inverse.
ProofLetX,Ybe Drazin inverses ofA,withX Am+1=AmandY An+1=An,respectively.SetE=AX=X A,F=AY=Y A.It is clear thatE2=E,F2=F.Thus fork=max{m,n},we have

ThenE=Fand

meaning that the Drazin inverse is unique.
In fact,the existence of the Drazin inverse of a complex matrix is given by the following Theorems 10.3–10.6.Customarily,the Drazin inverse ofAis denoted byAD.The smallest positive integer satisfying the equations(10.67)is called the Drazin index ofA,which is consistent with the index of a complex matrix of[11].For convenience,we still denote the Drazin index ofAby ind(A).If ind(A)=1,thenAis said to be group invertible.
Theorem 10.3([2,pp.146,Theorem8])LetA=,whereDis invertible andNis nilpotent.ThenAD=.
Proof LetX=.It is easy to check thatXsatisfies the equationsX Ak+1=Ak,for some positive integerk X=AX2,AX=X A.Therefore.
Theorem 10.4([2,pp.145,Theorem7])LetA∈Cn×nand ind(A)=k.Then there exists a polynomialq(x)such thatAD=Al(q(A))l+1for anyl≥k.
ProofLetA=,whereDis invertible andNis nilpotent.SinceDis invertible,there exists a polynomialq(x)such thatD−1=q(D).Then for anyl≥k,we have

It is easy to checkAl(q(A))l+1==AD.
Theorem 10.5([2,pp.148,Ex.39],seealso[16,Theorem5])LetA∈Cn×nand ind(A)=k.Then for(A2l+1)(1)∈A2l+1{1},AD=Al(A2l+1)(1)Alfor anyl≥k.In particular,AD=Al(A2l+1)†Al.
ProofLetA=P,whereDis invertible andNis nilpotent.ThenA2l+1=for anyl≥k.Let(A2l+1)(1)∈A2l+1{1}.Then(A2l+1)(1)=for someX1,X2andX3.Hence it is easy to obtainAl(A2l+1)(1)Al=AD.
Theorem 10.6([16])LetA∈Cn×n.We perform a sequence of full rank decompositions:

Then there exists a positive integerksuch thatHk Gk=0 orHk Gkis invertible.In this case,

ProofIfHi Giis ap×pmatrix and has rankq Letkbe the smallest positive integer such thatHk Gk=0 orHk Gkis invertible. (1)Assume thatHk Gkis invertible.IfGk∈Cp×r,Hk∈Cr×p,then rank(Hk−1Gk−1)=rank(Gk Hk)=raccording to thatHk−1Gk−1=Gk Hkis a full rank decomposition.SinceG1(···Gk x)=02(···Gk x)=0=0,we have thatG1···Gkis of full column rank.Similarly,we can obtainHk···H1is of full row rank.HenceG1···Gk(Hk Gk)is of full column rank.Since is a full rank decomposition,we have rank(Ak)=rank(G1···Gk)=r.Also, is a full rank decomposition,we have rank(Ak+1)=r.Sincekis the smallest positive integer,we have ind(A)=k.LetX=G1···Gk(Hk Gk)−(k+1)Hk···H1.ThenX=AD. (2)Assume thatHk Gk=0.ThenAk+1=0,it follows thatAD=0. In this section,we first give the definition of the Drazin inverse in semigroups or rings.Then we present some basic properties of the Drazin inverse.Finally,we study the core-nilpotent decomposition. Definition 11.1[19]Leta,x∈S.Thenxis called the Drazin inverse ofaif there exists a positive integerksuch that The smallest positive integerksatisfying the above equations is called the Drazin index ofa,denoted by ind(a).If ind(a)=1,thenais called group invertible. The next theorem shows that the Drazin inverse of an element in semigroups or rings is unique if it exists.The proof is similar to that of Theorem 10.2,here we omit it. Theorem 11.2([19,Theorem1])Leta∈S.Thenahas at most one Drazin inverse inS. If the Drazin inverse ofaexists,we denote the unique Drazin inverse ofabyaD.The notationaπmeans 1−aaDfor any Drazin invertible elementa∈S. Theorem 11.3([19,Theorem4])Leta∈S.Thenais Drazin invertible if and only if there existx,y∈Sand a positive integerkand we haveak=ak+1x=y ak+1.In this case, ProofIt is trivial to prove the necessity.Conversely,suppose that there existx,y∈Sand a positive integerkand we haveak=ak+1x=y ak+1.Then,we haveak x=y ak+1x=y ak,whence,by induction,ak xm=y mak(m=1,2,···).Thus our choicez=ak xk+1can equivalently be writtenz=yk+1ak,and we have by symmetry.By another induction,ak=am+k xm(m=1,2,···)and so And Hencezis the Drazin inverse ofa.In this case,aD=ak xk+1=y k+1ak,and ind(a)≤k. Theorem 11.4([20,Theorem2.2])Leta1,a2,d∈S.Ifa1anda2are both Drazin invertible,thenda1=a2dimplies. ProofWritingyi=(i=1,2),we haveai yi=yi ai,yi ai yi=yi,andfor suitablek∈N+.Since for anyj=2,3,···,it follows thatda1=a2dimplies.Then we find Dually,interchanginga1witha2andy1withy2while also reversing the order of terms in each monomial,we have Hencey2d=y2(a2d)y1=y2(da1)y1=dy1,as required. The next two theorems show that the relationships between Drazin invertibility ofaand Drazin invertibility(group invertibility)ofan. Theorem 11.5([19,Theorem2])Leta∈Sandn≥1 be a positive integer.ThenaDexists if and only if(an)Dexists.In this case, ProofSuppose thataD=xwith ind(a)=k.Then for arbitrary positive integerj,we haveak=ak+1x=a(ak+1x)x=ak+2x2=···=ak+j xjandx=x2a=x(x2a)a=x3a2=···=xj+1aj.Letqbe the unique positive integer satisfying 0≤nq−k Thus(an)D=xn=(aD)nwith ind(an)≤q.Finally ind(an) Conversely,suppose(an)D=ywith ind(an)=m.Then we havey(an)m+1=(an)m,an y2=y,an y=yan.By induction,we gety=y i+1ainandamn+1=a(an)m=a(an)m+1y=an+1(an)m+1y2=···=ain+1(an)m+1yi+1for arbitrary positive integeri. Setx=an−1y.In what follows,we proveaD=x. HenceaDexists with ind(a)≤mn. Theorem 11.6([30,Proposition4.5])Leta∈S.ThenaDexists if and only if there exists a positive integern≥1 such that(an)#exists.In this case, ProofSuppose thatx=aDwith ind(a)=n.Sety=xn.Then we have Therefore(an)#=y=(aD)n. On the contrary.Letx=an−1(an)#.We prove thatxis the Drazin inverse ofa.In fact, HenceaDexists andaD=an−1(an)#. The core-nilpotent decomposition in a ring was introduced by Patr´ıcio and Puystjens[39]. Definition 11.7([39,Definition9])Leta∈R.Then the suma=a1+a2is called the core-nilpotent decomposition ofa,if the following conditions hold: (1)a1is group invertible. (3)a1a2=a2a1=0. Wherea1is called the core part ofaanda2is called the nilpotent part ofa. Theorem 11.8([39,Lemma8])Leta∈R.ThenaDexists if and only ifahas a core-nilpotent decomposition. ProofSuppose thataDexists with ind(a)=k.Seta1=aaD aanda2=a−aaD a=(1−aaD)a.Then we havea1a2=(aaD a)(1−aaD)a=(aaD a−aaD a2aD)a=0 anda2a1=(1−aaD)a(aaD a)=a2aD a−aaD a2aD a=0.Hencea1a2=a2a1=0.By induction,we obtain=((1−aaD)a)k=(1−aaD)ak=0.Next,we prove thatexists.SinceaD a1=aD(aaD a)=(aaD a)aD=a1aD,a1(aD)2=aaD a(aD)2=aDandaD(a1)2=aD(aaD a)2=a4(aD)3=aaD a=a1,we haveexists with=aD. Conversely,Leta=a1+a2be core-nilpotent decomposition ofa.Then there exists a positive integerksuch thatexists,=0 anda1a2=a2a1=0.By induction,ak=.Then,decompositions and=.HenceaDexists withaD=. Remark 11.9[39]The core-nilpotent decomposition is unique.In fact,leta∈R.Suppose thata=a1+a2anda=b1+b2are the core-nilpotent decompositions ofa.By Theorem 11.8,we know that.Thereforea2=a−a1=a−b1=b2,the uniqueness of core-nilpotent decomposition is proved. In this section,e∈Ris an idempotent.we denoteeRe+1−e={exe+1−e:x∈R}.It should be stressed that this set is a semigroup.The subrings of the formeReare called corner rings.We first start with elementary lemmas which will be useful in proving our results. Lemma 12.1([40,Theorem1])Lete∈Rbe an idempotent.Then for allx∈R,the following statements hold: (1)exe+1−eis invertible inRif and only ifexeis invertible in the ringeRe.In this case, and (2)exe+1−eis regular inRif and only ifexeis regular in the ringeRe.In this case, and (3)exe+1−eis group invertible inRif and only ifexeis group invertible in the ringeRe.In this case, and (4)exe+1−eis Drazin invertible with indexkinRif and only ifexeis Drazin invertible with indexkin the ringeRe.In this case, and IfA∈Rm×nis regular,A−,A=∈A{1},thenAA−andA=Aare two idempotents.We next relate Drazin inverses and the classical inverse between the semigroup and the semigroup using Lemma 12.1. Proposition 12.2([40,Proposition3])LetA∈Rm×nbe a regular matrix with inner inversesA−andA=,andB∈Rm×m.Then the following conditions are equivalent: (1)Γ=AA−B AA−+Im−AA−is an invertible matrix. (2)Ω=A=AA−B A+In−A=Ais an invertible matrix. Moreover, and also ProofIfAA−B AA−+Im−AA−is invertible inRm×m,then it follows from Lemma 12.1(1)thatAA−B AA−is invertible in the ringAA−Rm×m AA−.Therefore,there exists anX∈AA−Rm×m AA−such thatAA−B AA−X=X AA−B AA−=AA−.Multiplying on the left byA=and on the right byA,and asAA−X=X AA−=X,then and Hence,(A=A)A−B A(A=A)is invertible in the ringA=ARn×n A=Aand thusA=AA−B A+In−A=Ais an invertible matrix. The converse is analogous.To proveA=AA−Γ−1A+In−A=Ais the inverse ofΩ,we remark that The expression of the inverse ofΓcan be verified analogously. Proposition 12.3([40,Proposition4])LetA∈Rm×nbe a regular matrix with inner inversesA−andA=,andB∈Rm×m.Then the following conditions are equivalent: (1)Γ=AA−B AA−+Im−AA−is a regular matrix. (2)Ω=A=AA−B A+In−A=Ais a regular matrix. Moreover, and also ProofIfΓis regular,then Conversely,ifΩis regular,then Theorem 12.4([40,Proposition5])LetA∈Rm×nbe a regular matrix with inner inversesA−andA=,andB∈Rm×m.Then the following conditions are equivalent: (1)Γ=AA−B AA−+Im−AA−is Drazin invertible with indexk(group invertible ifk=1). (2)Ω=A=AA−B A+In−A=Ais Drazin invertible with indexk(group invertible ifk=1). Moreover, and also ProofLet us first consider the casek=1,i.e.,the group invertibility case.IfΓ#exists,then by Lemma 12.1 and Proposition 12.3 and furthermore Thus sinceAA−Γ#=Γ#AA−.In fact,using Lemma 12.1(3),it follows that and henceAA−Γ#=Γ#AA−.Therefore, Conversely,ifΩ#exists then and also So, sinceA=AΩ#=Ω#A=A,usingΩ#∈A=ARn×n A=A+In−A=Aby Lemma 12.1(3).Therefore, For the general case,supposeΓhas indexk,i.e.,ΓDexists.Then exists.Using the first part of the proof and keeping in mind thatBis arbitrary, is group invertible.Thus,ΩDexists.Moreover,and using Theorem 11.6, The converse is analogous.For the expression ofΓD, In this section,we first give some auxiliary lemmas.Then we present Jacobson’s Lemma and Cline’s formula for Drazin inverses. Lemma 13.1([8,Lemma2.2])Letabe a regular element with an inner inversea−.Then,given a positive integern, ProofThe proof is by induction onn.Denote It is clear thatz=x+a(1−aa−).Assume(13.68)to hold fork,we will prove it fork+1. We note that Now,by the induction step, Lemma 13.2([8,Lemma2.3])Leta,b∈R.Then,given a positive integern, wherer=−ab)j. ProofThis can be easily proved by induction onn. The following lemma is an answer to a question raised by Patr´ıcio and Veloso in[41]about the equivalence between the conditions ind(a2a−+1−aa−)=kand ind(a+1−aa−)=k,and provides a new characterization of the Drazin index. Lemma 13.3([8,Theorem3.1])Letabe a regular noninvertible element with an inner inversea−.Then the following conditions are equivalent: (1)ind(a)=k+1. (2)ind(a2a−+1−aa−)=k,for one and hence all choices ofa−∈a{1}. (3)ind(a+1−aa−)=k,for one and hence all choices ofa−∈a{1}. Proof(1)(2).Whenk=0,we get Corollary 2.8.So we may considerk≥1. Firstly,note thatak+1a−=(a2a−)k,fork≥1,and secondlya2a−∈eRe,wheree=aa−,from which(a2a−)D∈eRewith indexkif and only if ind(a2a−+1−aa−)=kby Lemma 12.1. If ind(a2a−+1−aa−)=k,then ind(a2a−)=k.This means(a2a−)k+1R=(a2a−)k RandR(a2a−)k+1=R(a2a−)k,which in turn givesak+2R=ak+1RandRak+2=Rak+1.Hence,ind(a)≤k+1.Now,if ind(a)=l≤kthenal+1a−R=al+1R=al R=al a−R,from which(a2a−)l R=(a2a−)l−1R,and thereforek=ind(a2a−)≤l−1 Conversely,if ind(a)=k+1 thenak+2a−R=ak+1a−RandRak+2a−=Rak+1a−,which give(a2a−)k+1R=(a2a−)k RandR(a2a−)k+1=R(a2a−)k.Therefore,ind(a2a−)≤k.Assuming ind(a2a−)=l (2)(3).Denote Assume that ind(x)=k,or equivalently,ind(a)=k+1.Thenxk R=xk+1Randak+1=ak+2wfor somew∈R.By(13.68), This givesz k R=z k+1R.On the other hand,since ind(x)=kwe also havexk=uxk+1for someu∈R.By(13.68), From this we conclude thatRz k=Rz k+1.Consequently,ind(z)≤k. By symmetrical arguments,we can show that ind(z)=kimplies that ind(x)≤k.Furthermore,if ind(z) Lemma 13.4([8,Theorem3.4])Leta,b∈R.Then(1−ab)+is a reflexive inverse of 1−ab,then a reflexive inverse of 1−bais given by wherep=1−(1−ab)+(1−ab)andq=1−(1−ab)(1−ab)+. ProofLetx=1+b((1−ab)+−pq)a.Then(1−ba)x=1−bqa.Furthermore,(1−ba)x(1−ba)=1−ba−bq a(1−ba)=1−baand where we have simplified by writingab=1−(1−ab)and using the relations(1−ab)(1−ab)+(1−ab)=1−aband(1−ab)+(1−ab)(1−ab)+=(1−ab)+. Theorem 13.5([8,Theorem3.5])Leta,b∈R.If 1−abis group invertible,then 1−bais group invertible and ProofLetx=1+b((1−ab)#−(1−ab)π)a.First,we note that(1−ab)#is a reflexive inverse that commutes with 1−ab.In view of the preceding Lemma 13.4 we have thatxis a reflexive inverse of 1−ba.Next,we will prove thatxcommutes with 1−ba.We have and,similarly,(1−ba)x=1−b(1−ab)πa,which givesx(1−ba)=(1−ba)x.Thereforexsatisfies the three equations involved in the definition of group inverse. Theorem 13.6([8,Theorem3.6])Leta,b∈R.If 1−abis Drazin invertible with ind(1−ab)=k,then 1−bais Drazin invertible with ind(1−ba)=kand wherer−ab)j. ProofAssume that ind(1−ab)=k≥2.Then(1−ab)kis group invertible and Lemma 13.3 leads to ind=0.By Lemma 13.2,we have wherer−ab)j.From the above relations,1−rab(1−ab)k((1−ab)k)#is invertible and by[11,Theorem 2.19],we have that 1−b(1−ab)(1−ab)D rais invertible.Furthermore, From this it follows that On the other hand, and hence(1−ba)k=(1−ba)2k(1−b(1−ab)(1−ab)D ra)−1∈(1−ba)k+1R.Therefore(1−ba)k∈R(1−ba)k+1∩(1−ba)k+1R,which implies that ind(1−ba)≤k. Furthermore,analysis similar to that of the last part of the proof of Lemma 13.3 shows that ind(1−ba)=k.Now,(1−ba)D=((1−ba)k)#(1−ba)k−1.In view of(13.2)and applying Theorem 13.5,it follows that Hence, In 1965,Cline[15]proved that ifabis Drazin invertible,thenbais Drazin invertible.In this case,(ba)D=b((ab)D)2a.This equality is called Cline’s formula. Theorem 13.7([15])Leta,b∈R.Thenab∈R Dif and only ifba∈RD.In this case, ProofThe sufficiency of the theorem is easy to obtain by the symmetry ofaandb.We only need to prove the necessity.Suppose thatab∈RDwith ind(ab)=k,then we haveab(ab)D=(ab)D ab,ab((ab)D)2=(ab)D,(ab)k+1(ab)D=(ab)k.Then we prove thatba∈RD.Letx=b((ab)D)2a.Then Hence(ba)x=x(ba). Henceba∈RDwith ind(ba)≤k+1,and(ba)D=b((ab)D)2a. In this section,we first start with some lemmas which will be useful in proving our main results. Lemma 14.1([53,Lemma1]) (1)Ifa,b∈Rwithab=baandais nilpotent,thenabis nilpotent. (2)Ifa,b∈Rare nilpotent andab=ba,thena+bis nilpotent. Lemma 14.2([53,Lemma2])Leta,b∈Rbe Drazin invertible andab=ba.Then (1)a,b,aDandbDcommute. (2)abis Drazin invertible,and(ab)D=bD aD. Proof(1)By Theorem 11.4,we have thatab=bagivesaD b=baD.So isaD bD=bD aD.Hencea,b,aDandbDcommute each other. (2)Letx=bD aD.The commutativity ofabandxis obvious,and it is easily verified thatxabx=x.Finally,ab−(ab)2xis nilpotent by using Lemma 14.1 and the splittingab−(ab)2x=abbπ+b2bD aaπ,whereaaπandbbπare both nilpotent. The next theorem characterizes the relationships of the Drazin invertibility between ofa+band 1+aD b,and gives the explicit expressions of the Drazin inverse. Theorem 14.3([53,Theorem3])Leta,b∈Rbe Drazin invertible andab=ba.Then 1+aD bis Drazin invertible if and only ifa+bis Drazin invertible.In this case,we have and ProofSupposeξ=1+aD bis Drazin invertible,then by Lemma 14.2,a,b,aD,bD,ξandξDcommute with each other.Sinceaaπis nilpotent,we get 1+aaπbDis invertible.In a similar way,we conclude that 1+bbπaDis invertible. Letx=ξD aD+bD(1+aaπbD)−1aπ.In what follows,we show thatxis the Drazin inverse ofa+b,i.e.,the following conditions hold:(i)(a+b)x=x(a+b);(ii)x(a+b)x=x;(iii)(a+b)−(a+b)2xis nilpotent. (i)By Lemma 14.2,a+bandxcommute. (ii)After a calculation we obtain Then we can simplify Note thataD aπ=0,then we have (iii)We have Sinceaaπ,bbπandξξπare nilpotent,it follows that(a+b)−(a+b)2xis nilpotent by Lemma 14.1. In order to show another expression(a+b)D,it is sufficient to prove Noting the commutativity and we derive Observing that 1−(1+bbπaD)−1ξξπis invertible since(1+bbπaD)−1ξξπis nilpotent,we know Thus Now we get Hence Conversely,ifa+bis Drazin invertible,we can rewrite 1+aD b=a1+b1,wherea1=aπandb1=aD(a+b).Note thata1is idempotent andaDis group invertible with(aD)#=a2aD.Then by Lemma 14.2(2),we know thatb1is Drazin invertible and In addition, Therefore we can derive(a1+b1)D,wherea1andb1satisfy the sufficient conditions.That is,1+aD bis Drazin invertible and the formula is presented as follows: The proof is completed. Corollaryn 14.4([53,Corollary4])Leta,b∈Rbe Drazin invertible with ind(a)=k,ind(b)=l,ab=ba.If 1+aD bis Drazin invertible,thena+bis Drazin invertible and ProofFrom ind(a)=k,it follows that(aaπbD)k=0.Thus Similarly, Using Theorem 14.3,we obtain the above formulae. Proposition 14.5Leta,b∈Rbe group invertible withab=ba.Thena+bis group invertible if and only if 1+a#bis group invertible.In this case, and ProofIt is similar to the proof of Theorem 14.3. In this section,we first begin with some elementary and known results which play an important role in main results.In what follows,unless otherwise stated,pandqmean two arbitrary idempotents in a ringR.Then we give some equivalent conditions for the Drazin invertibility ofp−q,pq,pq−q pandpq+q p. Lemma 15.1([19,Corollary1])Leta,b∈R Dandab=ba=0.Then(a+b)D=aD+bD. ProofFrom Lemma 14.2(1),we have and,choosingmso large thatam=am+1bD,bm=bm+1bD,we have Therefore,the result now follows. Lemma 15.2([12,Lemma2.5])Leta,b∈R Dandp2=p∈R.Ifap=paandbp=pb,thenap+b(1−p)∈R Dand ProofSincep2=p,we havepD=p.Thus,a,b,p∈RD.Note thatap=paandbp=pb.We obtain(ap)D=aD pand(b(1−p))D=bD(1−p)by Lemma 14.2(2).Asapb(1−p)=b(1−p)ap=0,according to Lemma 15.1,it follows that(ap+b(1−p))D=aD p+bD(1−p). Lemma 15.3([12,Lemma2.6])Leta∈R,p2=p∈R,b=pa(1−p)andc=(1−p)ap.The following statements are equivalent: (1)b+c∈RD. (2)bc∈RD. (3)b−c∈RD. Proof(1)(2).Since(b+c)2=bc+cbandb+c∈R D,we havebc+cb∈R D.Letx=(bc+cb)D.Asp(bc+cb)=(bc+cb)p,we obtain thatpx=xpby Lemma 14.2(2).Next,we prove that(bc)D=pxp. Sincex=(bc+cb)x2,we get By(bc+cb)x=x(bc+cb),we obtainp(bc+cb)xp=px(bc+cb)p.It follows thatbc(pxp)=(pxp)bc. Because(bc+cb)n+1x=(bc+cb)nfor some positive integern,we have Multiplying the equation above bypon two sides yields i.e.,(bc)n+1pxp=(bc)n.So,bcis Drazin invertible and(bc)D=pxp. (2)(1).According to Lemma 13.7,bc∈RDis equivalent tocb∈RD.Note thatbccb=cbbc=0.We have(b+c)2=bc+cb∈RDby Lemma 15.1.It follows thatb+c∈RD. (2)(3).Its proof is similar to(1)(2). Lemma 15.4([12,Lemma2.7])Leta∈Rwitha−a2∈RDora+a2∈RD.Thena∈RD. ProofWe only need to prove the situation whena−a2∈RDwithx=(a−a2)D.By Lemma 11.4,it is clearax=xasincea(a−a2)=(a−a2)a.Sincea−a2∈RD,we get(a−a2)n=(a−a2)n+1xfor some positive integern≥1,that is, Note that It follows that This showsan∈an+1R∩Ran+1.Hence,a∈R Dby Theorem 11.3. Proposition 15.5([12,Proposition3.1])The following statements are equivalent: Proof(1)(6)is obvious by Lemma 13.6.We only need to prove that(1)-(5)are equivalent. (1)(4).It is clear that 1−pq=1−p(pq).Thus,1−pqis Drazin invertible if and only if 1−pq pis Drazin invertible by Lemma 13.6. (4)(5).Sincep∈RDandp(1−pq p)=(1−pq p)p=p−pq p,we obtain thatp−pq pis Drazin invertible according to Lemma 14.2(2). (5)(4).Supposea=p−pq p,b=1.Thenaandbare Drazin invertible.Since 1−pq p=(p−pq p)+1−p,it follows that 1−pq p=ap+b(1−p)is Drazin invertible in view of Lemma 15.2. (2)(5).Sincep−pq=pp(1−q)andp−pq p=p(1−q)p,the result follows by Lemma 13.7. (2)(3).By Lemma 13.7,p(1−q)∈RDif and only if(1−q)p∈R D. Finally,the other equivalences follow by interchangingpandq. By replacingpandqwith 1−pand 1−qin Proposition 15.5,respectively.We get the following result immediately. Corollary 15.6([12,Corollary3.2])The following statements are equivalent: Finally,asp−pq∈R Dappears in Proposition 15.5 and Corollary 15.6(18),we get the following result. Corollary 15.7([12,Corollary3.3])Statements(1)-(10)of Proposition 15.5 are equivalent with statements(11)-(20)of Corollary 15.6. In 2012,Koliha,Cvetkovi´c-Ili´c and Deng[29]proved thatp−q∈ADif and only if 1−pq∈ADif and only ifp+q−pq∈AD,wherep,qare idempotents in a Banach algebraA.It is natural to consider whether the same property can be inherited to the Drazin inverse of ring versions.The following result proves that the statement holds in the ring case. Theorem 15.8([12,Theorem3.4])The following statements are equivalent: (1)p−q∈R D. (2)1−pq∈RD. (3)p+q−pq∈RD. Proof(1)(2).Asp(p−q)2=(p−q)2p=p−pq p,then 1−pq p=(p−q)2p+1−p. Leta=(p−q)2andb=1.Thenap=pa,bp=pb.Sincep−q∈RD,we obtain thata=(p−q)2∈R D.By Lemma 15.2,1−pq p=ap+b(1−p)∈RD.Therefore,1−pqis Drazin invertible by Lemma 13.6. (2)(3).This is Corollary 15.7(2)(11). (3)(1).Leta=1−pq p,b=1−(1−p)(1−q)(1−p).Thenap=pa,bp=pbanda∈R Dby Corollary 15.7.As 1−(1−p)(1−p)(1−q)=p+q−pq∈R D,thenb∈R Dby Lemma 13.6.Finallyap+b(1−p)=(p−q)2∈RDby Lemma 15.2,hencep−q∈R D. Cvetkovi´c-Ili´c,Deng[18]considered the Drazin invertibility of product and difference of idempotents in a Banach algebraA.Moreover,they proved that if one ofpq,1−p−qand(1−p)(1−q)belongs toADthen they all do.We extend the result in[18]to the ring cases. Theorem 15.9([12,Theorem3.5])The following statements are equivalent: (1)pq∈RD. (2)1−p−q∈RD. (3)(1−p)(1−q)∈RD. Proof(1)(2).Let¯p=1−p.Then¯p−q∈RDif and only ifq−¯pq∈RDby Proposition 15.5 and Theorem 15.8.Since¯p−q=1−p−qandq−¯pq=pq,(1)(2)holds. (1)(3).Set¯p=1−p.Then¯p−¯pq∈RDif and only ifq−¯pq∈R Dby Proposition 15.5.Since¯p−¯pq=(1−p)(1−q)andq−¯pq=pq,the result follows. Theorem 15.10([12,Theorem3.6])The following statements are equivalent: (1)pq−q p∈RD. (2)pq∈RDandp−q∈RD. ProofPoseb=pq(1−p)andc=(1−p)q p.Thenb−c=pq−q p. (1)(2).As by hypothesisb−c∈RD,thenpq p−(pq p)2=pq(1−p)q p=bc∈RDby Lemma 15.3.It follows thatpq p∈RDby Lemma 15.4,hencepq=p(pq)∈RDby Lemma 13.7. Similarly,(1−p)q−q(1−p)=−(pq−q p)∈RDimpliesq−pq=(1−p)q∈R D.Therefore,p−q∈RDby Proposition 15.5 and Theorem 15.8. (2)(1).By Lemma 13.7,bothpq pand(p−q)2are Drazin invertible.Note thatbc=pq(1−p)q p=pq p(p−q)2=(p−q)2pq p.It follows thatbcis Drazin invertible by Lemma 14.2(2).Hence,according to Lemma 15.3,we havepq−q p=b−c∈R D. We can give an interesting result similar to Theorem 15.10. Theorem 15.11([12,Theorem3.7])The following statements are equivalent: (1)pq+q p∈RD. (2)pq∈RDandp+q∈RD. Proof(1)(2).Sincepq+q p=−(p+q)+(p+q)2=(p+q−1)+(p+q−1)2∈R D,p+q∈RDandp+q−1∈RDaccording to Lemma 15.4.Therefore,pq∈RDby Theorem 15.9. (2)(1).Sincepq+q p=(p+q)(p+q−1)=(p+q−1)(p+q),pq+q p∈RDby Lemma 14.2(2)and Theorem 15.9. Remark 15.12([12,Remark3.8])Letp,qbe two idempotents in a Banach algebra.Then,p+qis Drazin invertible if and only ifp−qis Drazin invertible[29].Hence,pq+q pis Drazin invertible is equivalent topq−q pis Drazin invertible in a Banach algebra.However,in general,this need not be true in a ring.For example,letR=Z,p=q=1.Thenp−q=0∈RD,butp+q=2/∈R D. Following the Drazin invertibility of product and difference of idempotents,we investigate the Moore-Penrose invertibility of the commutatorpq−q pand the anticommutatorpq+q pfor two projectionspandq,we need the following four lemmas. Lemma 15.13([51,Lemma11])The following conditions are equivalent for any two projectionspandqin a*-proper ringR: (1)(1−p)(1−q)∈R†. (2)1−p−q∈R†. (3)pq∈R†. ProofSubstitute 1−pforpin[11,Corollary 10.8]. Lemma 15.14([51,Lemma12])Letb=pq(1−p),wherepandqare two projections inR,thenb−b*∈RDif and only ifbb*∈R D.In this case,ind(bb*)≤ind((b−b*)2). ProofSee Lemma 15.3. Lemma15.15([51,Lemma13])Letr∈R.Ifr+r2∈R D(resp.,r−r2∈RD),thenr∈R Dand ind(r)≤ind(r+r2)(resp.,ind(r)≤ind(r−r2)). ProofSee Lemma 15.4. Theorem15.16([51,Theorem14])The following conditions are equivalent for any two projectionspandqin a*-proper ringR: (1)pq−q p∈R†. (2)pq∈R†andp−q∈R†. Proof(1)(2).Letb=pq(1−p).Sinceb−b*=pq−q p∈R†and(b−b*)R=(b*−b)R=((b−b*))*R,we have(b−b*)†=(b−b*)#by Theorem 9.3.It can be verified that((b−b*)†)2is the Moore-Penrose inverse of(b−b*)2.Again,by Theorem 9.3,it follows that((b−b*)2)†=((b−b*)2)#since((b−b*)2)*R=(b−b*)2R.In view of Lemma 15.14,we havebb*∈RDand ind(bb*)≤ind((b−b*)2)≤1. Note thatbb*=pq(1−p)q p=pq p−(pq p)2.By Lemma 15.15,we obtainpq p∈RDand ind(pq p)≤ind(bb*)≤1,which meanspq p∈R#.Hence(pq p)†=(pq p)#because(pq p)*R=pq pRby Theorem 9.3.Now,substitutingpqforrin[11,Theorem 8.7],one can see thatpq∈R†. Thus,pq−q p∈R†impliespq∈R†.Replacingpby(1−p),we get(1−p)q∈R†since(1−p)q−q(1−p)=−(pq−q p)∈R†.In addition,we havep−q∈R†by[11,Corollary 10.8]. (2)(1).It follows that(p−q)(p−q)†=(p−q)†(p−q)sincep−q∈R†and(p−q)*=p−q.One can easily check that((p−q)†)2is the Moore-Penrose inverse of(p−q)2.Also,we havepq p∈R†sincepq∈R†.Meanwhile,((p−q)2)*=(p−q)2,(pq p)*=pq pandbb*=pq p(p−q)2=(p−q)2pq p.Combining these facts we can see thatpq p,(pq p)†,(p−q)2and((p−q)2)†commute with each other according to[33,Corollary 12].Now,it is trivial to verify that(pq p)†((p−q)†)2is the Moore-Penrose inverse ofbb*=pq p(p−q)2.Moreover,it is clear thatb∈R†by[11,Theorem 8.7].Finally,pq−q p∈R†follows by[4,Theorem 4.1(iv)](see also[31,Theorem 13]). Theorem 15.17([51,Theorem15])The following conditions are equivalent for any two projectionspandqin a*-proper ringR: (1)pq+q p∈R†. (2)p+q∈R†andpq∈R†. Proof(1)(2).According to Theorem 9.3,it follows that(pq+q p)†=(pq+q p)#sincepq+q p∈R†and(pq+q p)*R=(pq+q p)R.Note that(p+q)2−(p+q)=(p+q−1)2+(p+q−1)=pq+q p∈R#.By Lemma 15.5,we havep+q,p+q−1∈RDwith ind(p+q)≤ind(pq+q p)≤1 and ind(p+q−1)≤ind(pq+q p)≤1,i.e.,p+q,p+q−1∈R#.On the other hand,(p+q)*R=(p+q)Rand(p+q−1)*R=(p+q−1)Rimply(p+q)†=(p+q)#and(p+q−1)†=(p+q−1)#by Theorem 9.3.Finally,by Lemma 15.3,we havepq∈R†sincep+q−1∈R†. (2)(1).First,pq∈R†impliesp+q−1∈R†by Lemma 15.3.Combining this with the hypothesisp+q∈R†and the facts(p+q)*=p+q,(p+q−1)*=p+q−1 andpq+q p=(p+q)(p+q−1)=(p+q−1)(p+q),one can see thatp+q,p+q−1,(p+q−1)†and(p+q)†are commutative with each other by[33,Corollary 12].Whence it is straightforward to check that(pq+q p)†=(p+q)†(p+q−1)†. LetAbe anm×nregular matrix over a ring,andTbe a square matrix withT k=P AQfor some matricesPandQ.In this section,we give necessary and sufficient conditions for a productP AQwithP′P A=A=AQQ′to have Drazin inverse,and the formulae for obtaining the Drazin inverse if the conditions are satisfied. Theorem 16.1([10,Theorem2.1])LetAbe am×nregular matrix over a ring,andTbe a square matrix withT k=P AQfor some positive integerkand matricesPandQ.Then the following statements are equivalent: (1)Thas a Drazin inverseT Dwith ind(T)≤kand there exist matricesP′andQ′such thatP′P A=A=AQQ′. (2)A−AQT P A+In−A−Ais invertible. In this case, Proof(1)(2).LetX=T D.ThenT k=T k+1X,T X=X T,X=T X2.Hence, Thus,by(16.70),we have Multiplying the equality above byP′andQ′on the left and right sides respectively,we obtain by the hypothesis.Therefore we get Similarly,we have Thus,it follows that and that is,A−AQT P A+In−A−Ais invertible. (2)(1).If we writeN=A−AQT P A+In−A−A,thenNis invertible.Thus there existsYsuch thatIn=Y N=N Y.Hence and PutP′=AY A−AQT,Q′=T P AY.ThenP′P A=A=AQQ′. LetX=P AN−1Q.We shall show thatXis a Drazin inverse ofTwith ind(T)≤k.First of all,it is easy to verify that and Thus Next,we have Note thatT k=P AQand we have Similarly, SetM=A−AQP A+In−A−AandS=A−AQT2P A+In−A−A.ThenN2=M S=S M.SinceNis invertible,so isM,andM−1=N−2S=S N−2.Thus and whenceT X=X T.This completes the proof of Theorem 16.1. Letk=1 in Theorem 16.1.Then we have Corollary 16.2([10,Corollary2.1])LetAbe am×nregular matrix over a ring,andTbe a square matrix withT=P AQfor some matricesPandQ.Then the following statements are equivalent: (1)Thas a group inverseT#and there exist matricesP′andQ′such thatP′P A=A=AQQ′. (2)A−AQP A+In−A−Ais invertible. In this case, ProofSinceT=P AQ,one has Thus,Corollary 16.2 follows from Theorem 16.1. Corollary 16.3([10,Corollary2.2])LetEbe an×nidempotent matrix,andTbe a square matrix such thatT k=P E Qfor some positive integerkand matricesPandQ.Then there exist matricesP′andQ′such thatP′P E=E=E QQ′andThas a Drazin inverseT Dwith ind(T)≤kif and only ifE QT P E+In−Eis invertible.In this case, ProofSinceEis idempotent,we haveE−=E.Thus Corollary 16.3 follows from Theorem 16.1. Next,we give characterizations for existence of the Drazin inverse of a matrix over an arbitrary ring.Moreover,the Drazin inverse of a productP AQfor which there existP′andQ′such that can be characterized and computed.This generalizes results obtained for the group inverse of such products. Lemma 16.4([42,Lemma])LetTbe an×nmatrix over a ring.The following conditions are equivalent: (1)Thas a Drazin inverse with indexk. (2)There exists a matrixLandkis the smallest positive integer such that (3)There exist matricesMandNandkis the smallest positive integer such thatT k=T k+1N=M T k+1. (4)kis the smallest positive integer such thatT khas a group inverse(T k)#and,independent of the choice of(T k)−,also equivalent with. (5)kis the smallest positive integer such thatT kis regular andT2k(T k)−+In−T k(T k)−is invertible. (6)kis the smallest positive integer such thatT kis regular and(T k)−T2k+In−(T k)−T kis invertible. In this case,T k+nis regular for all positive integersnwithM n(k+1)T(n−1)kbelonging toT k+n{1}and which shows thatT Dis always equivalent withT2k−1.Moreover,(T D)#exists and equalsT2T D. Proof(1)(2)(3).It is clear. (3)(1).Suppose thatT k=M T k+1=T k+1N,then and more generally, It follows that(T2k)−and(T2k+1)−exist. Now,we prove by straightforward computation that is the Drazin inverse ofTof indexk. (I)We claim thatT D=T k(T2k)−T2k−1(T2k)−T k. In fact,it follows from(3)that: Then, We verify now the three definition equations: (II)We claim thatT D=T k(T2k+1)−T k. In fact,we verify the three definition equations: (3)(4).It follows from(3)that implies the existence of(T k)#.Conversely,if(T k)#exists,for the smallest positive integerk,thenT k−1(T k)#is the Drazin inverse ofTsince there exists a matrixGsuch thatT k=GT2k=T2k G,from which follows that: and Moreover, implies (4)(5)(6).Follows from Theorem 3.1.Moreover, i.e.,T Dis always equivalent withT2k−1. Finally,it follows from(2)that: and therefore that(T D)#always exists,ifT Dexists.Since we have Theorem 16.5([42,Theorem])LetAbe an×nmatrix overRandP,Qmatrices overRfor which there exist matricesP′,Q′such thatP′P A=A=AQQ′.LetA1:=Aand for all positive integersi>1,let Then the following statements are equivalent: (1)T=P AQhas a Drazin inverse with indexk. (2)kis the smallest positive integer such thatAkis regular andis invertible. (3)kis the smallest positive integer such thatAkis regular andis invertible and independent of the choice of. In that case,withUk:=−Ak,we have ProofThas a Drazin inverse with indexkif and only ifkis the smallest positive integer such thatT khas index 1.But, andAQT k−2P Ais regular if and only ifT kis regular,because there existP′andQ′such thatP′P A=A=AQQ′.Indeed, is equivalent to Moreover,sinceP′P A=A=AQQ′,we have which means thatP′P Ak=Ak=Ak QQ′. We therefore can apply Corollary 3.3 withp=P,a=AQT k−2P Aandq=Q,which implies thatT khas index 1 if and only ifT kis regular andIn−Ak A−kis invertible if and only ifT kis regular andis invertible. Corollary 16.6([42,Corollary])LetTbe an×nregular matrix over a ring withT=T T(1,2)T.Then the following statements are equivalent: (1)Thas a Drazin inverse with indexk. (2)kis the smallest positive integer such thatTk:=T(1,2)T k T(1,2)is regular andis invertible. (3)kis the smallest positive integer such thatTk:=T(1,2)T k T(1,2)is regular andis invertible and independent of the choice of the reflexive inverse. In that case,and with we obtain Indeed,apply the theorem to the factorizationT=T T(1,2)TwithA=T(1,2),P=Q=TandP′=Q′=T(1,2). LetCbe an additive category.Suppose thatϕ,η:X→Xare two morphisms ofCwith the Drazin inverseϕDandηD,respectively.In this section,we mainly investigate the Drazin inverse of a sum of morphisms. In 1958,Drazin[19]proved(a+b)D=aD+bDprovided thata,b∈Rsatisfyingab=ba=0.In fact,similarly to the proof of Lemma 15.1,it is also valid for morphisms in an additive category.In 2009,Chen et al.[14]reduced the conditionϕη=ηϕ=0 to the conditionϕη=0 and proved thatϕ+ηis Drazin invertible. Theorem 17.1([14,Theorem2.1])LetCbe an additive category.Suppose thatϕ,η:X→Xare two morphisms ofCwith the Drazin inverseϕDandηDsuch thatϕη=0,thenϕ+ηhas the Drazin inverse with ind(ϕ+η)≤k1+k2−1,and wherek1=ind(ϕ),k2=ind(η). ProofLetω1=.Setω=ω1+ω2.Sinceϕη=0,we haveϕηD=ϕη(ηD)2=0,ϕDη=(ϕD)2ϕη=0.Thenϕω2=0 and Hence On the other hand, and Therefore Next we prove thatω(ϕ+η)ω=ω.Let Then we have or and Finally,we prove that(ϕ+η)mω(ϕ+η)=(ϕ+η)m,wherem=k1+k2−1.Fromϕη=0,we have Now forj=1,2,···,k1−1,we have Hence, Therefore,ωis the Drazin inverse ofϕ+η,i.e.,(ϕ+η)Dexists with ind(ϕ+η)≤k1+k2−1 and We observe that Theorem 17.1 answers the problem raised in the literature[50]. Corollary 17.2([14,Corollary2.2])LetCbe an additive category.Suppose thatϕ,η:X→Xare two morphisms ofCwith the group inverseϕ#andη#such thatϕη=0,thenϕ+ηhas the group inverse and(ϕ+η)#=(1X−ηη#)ϕ#+η#(1X−ϕϕ#). Cvetkovi´c-Ili´c[17]examined an additive problem of finding(a+b)Din terms of Drazin invertible ring elementsaandband their Drazin inverses.We find that the result also holds for morphisms in an additive category. Let us define forj∈N,the setUj={(p1,q1,p2,q2,···,pj,qj)=j−1,pi,qi∈{0,1,···,j−1},i=1,···j}. The following theorem is a generalization of[32,Theorem 2.1]to the category case.The proof below completely differs from the one presented in[32]. Theorem 17.3([17,Theorem2.1])LetCbe an additive category.Suppose thatϕ,η:X→Xare two morphisms ofCwith the Drazin inverseϕDandηD.Let ind(ϕ)=r,ind(η)=sandk∈N.If for every(p1,q1,p2,q2,...,pk,qk)∈Uk,thenϕ+ηis Drazin invertible and where ProofLet us denote the element on the right side of(17.76)byχ.We will prove that(ϕ+η)χ=χ(ϕ+η),χ2(ϕ+η)=χand(ϕ+η)l+1χ=(ϕ+η)l,for somel∈N.Denote by Hence,χ=y1+y2+y3.From(17.75)it follows thatϕηϕD=0 andϕηD=0.Also,we have that Therefore,by(17.78)we get and By computation using thatϕηD=0, where Using(17.78),we have On the other hand, Hence, Sinceϕη(ϕ+η)k−1=0,we have that y3(ϕ+η)=(ϕ+η)i−1,so by(17.79)and(17.81), Now,by(17.78)and using that y1ϕDϕ=y1andηDy2ϕ=y2−ηDϕπ,we get that(ϕ+η)χ=χ(ϕ+η).In order to prove thatχ2(ϕ+η)=χ,remark that y1y2=0,y3y1=0,y3y2=0 and=0.Thus we have We can easy verify the following Now,we will computey2y3.Sinceϕy1=ϕϕD,we get thatϕπϕy1=0,which together withϕηD=0 implies thatϕπϕy3=0.Now, Upon substituting these identities into(17.82),we have the following Now,sinceϕη(ϕ+η)k−1=0,y1ϕDϕ=y1andηD y2ϕ=y2−ηDϕπ,we get Letl,i∈N be such thati≥r+s−1 andl≥k+i−1.We will prove that Sincey3(ϕ+η)l=0,to prove(17.85),it is sufficient to prove that(y1+y2)(ϕ+η)l+1=(ϕ+η)l.Byϕη(ϕ+η)l=0,we get thaty1η(ϕ+η)l=0.Also,we have thaty2η(ϕ+η)l= so to prove(17.85),it is sufficient to prove that Sincei≥r+s−2, and we get that(17.87)holds.Hence,χ=(ϕ+η)D. Remark 17.4([17,Remark])Theorem 17.3 gives representations of(ϕ+η)Din the following particular cases: (1)ϕη=0. (2)ϕηϕ=0,ϕη2=0. (3)ϕηϕη=0,ϕηϕ2=0,ϕη2ϕ=0,ϕη3=0. In 2001,You and Chen[49]studied the group inverse of a sum of morphisms.In 2009,Chen et al.[14]extended the result of Huylebrouck[27]to the Drazin inverse and investigated the Drazin inverse of a sum of morphisms in an additive category. Theorem 17.5([14,Theorem2.3])LetCbe an additive category.Suppose thatϕ:X→Xis a morphism ofCwith the Drazin inverseϕDand ind(ϕ)=k1and thatη:X→Xis a morphism ofCsuch thatϕϕDη=η.Ifγ=(ϕ+η)ϕϕDhas the Drazin inverseγDwith ind(γ)=k2,thenϕ+ηhas the Drazin inverse with ind(ϕ+η)≤k1+k2and ProofLetq=ϕ2ϕD+η,s=η(1X−ϕϕD),γ=(ϕ+η)ϕϕD.Thenq=s+γand Henceshas the Drazin inverse with ind(s)=2 andsD=0.From Theorem 17.1,qhas the Drazin inverse with ind(q)≤k2+1,and Letp=ϕ(1X−ϕϕD).Thenϕ+η=p+q, Hence,phas the Drazin inverse with ind(p)=k1andpD=0.From Theorem 17.1,ϕ+η=p+qhas the Drazin inverse with ind(ϕ+η)≤k1+k2and Fromsγ=0,we havesγD=0.Then Furthermore,(q D)i=(γD)i+(γD)i+1sfor arbitraryi≥1.Note that Therefore, Corollary 17.6([50,Theorem1])LetCbe an additive category.Suppose thatϕ:X→Xis a morphism ofCwith the Drazin inverseϕDand ind(ϕ)=k1and thatη:X→Xis a morphism ofCsuch thatϕϕDη=ηand 1X+ϕDηis invertible,thenϕ+ηhas the Drazin inverse with ind(ϕ+η)≤k1+1 and whereξ=(1X+ϕDη)−1ϕD. ProofLetγ=(ϕ+η)ϕϕD.Next we proveγ#=ξ. Hence Then we haveγ#=ξ.From Theorem 17.5,ϕ+ηhas the Drazin inverse with ind(ϕ+η)≤k1+1 and Theorem 17.7([14,Theorem2.5])LetCbe an additive category.Suppose thatϕ:X→Xis a morphism ofCwith the Drazin inverseϕDand ind(ϕ)=k1and thatη:X→Xis a morphism ofCsuch thatϕDη=0.Ifγ=(ϕ+η)(1X−ϕϕD)has the Drazin inverseγDwith ind(γ)=k2,thenϕ+ηhas the Drazin inverse with ind(ϕ+η)≤k2+1 and Proof Letp=ϕ2ϕD.Thenphasp#=ϕD.Letq=ϕ(1X−ϕϕD)+η.Then we have Lets=ηϕϕD.Thenq=s+γands2=ηϕϕDηϕϕD=0.Henceshas the Drazin inverse with ind(s)=2 andsD=0, Then we havesγD=0.From Theorem 17.1,qhas the Drazin inverse with ind(q)=k,wherek≤k2+1. From Theorem 17.1,ϕ+ηhas the Drazin inverse with ind(ϕ+η)≤k,and HenceqϕD=(ϕ(1X−ϕϕD)+η)ϕD=ηϕD,q2ϕD=(ϕ+η−ϕ2ϕD)ηϕD=(ϕ+η)ηϕD.Note thatϕD(ϕ+η)=ϕDϕ,ϕD(ϕ+η)2=ϕDϕ(ϕ+η)=ϕ2ϕD.SinceϕD(ϕ+η)i=ϕiϕD,we haveϕD(ϕ+η)iη=ϕiϕDη=0.By induction,we knowq iϕD=(ϕ+η)i−1ηϕDfor arbitraryi≥1.Hence and Then Therefore,we have LetB=A+Ebe complex matrix withI+AD Einvertible.Wei and Wang[47],Wei[46]investigated the perturbation problem of group inverse and gave the sufficient and necessary condition ofB#=(I+AD E)−1AD.Castro-Gonz´alez et al.[6,7]investigated the sufficient and necessary condition ofB D=(I+AD E)−1AD.Chen et al.[14]generalized these results to the morphisms of an additive category. Theorem 17.8([14,Theorem3.1])LetCbe an additive category.Suppose thatϕ:X→Xis a morphism ofCwith the Drazin inverseϕDand ind(ϕ)=kand thatη:X→Xis a morphism ofCsuch that 1X+ϕDηis invertible.Let whereα=(1X+ϕDη)−1,β=(1X+ηϕD)−1.If 1X−γand 1X−δare invertible and thenf=ϕ+η−εhas the Drazin inverse with ind(f)≤k. ProofLet=αϕD.It is easy to verify thatαϕD=ϕDβ,ϕDε=εϕD=0. Then And we have Similarly,sinceϕ(ϕϕD−1X)η=0,we havef k=and Similarly we have Similarly we have Since 1X−γand 1X−δare invertible,we have Hence,fhas the Drazin inverse with ind(f)≤k,and Corollary 17.9([49,Proposition1])LetCbe an additive category.Suppose thatϕ:X→Xis a morphism ofCwith the group inverseϕ#and thatη:X→Xis a morphism ofCsuch that 1X+ϕ#ηis invertible.Let whereα=(1X+ϕ#η)−1,β=(1X+ηϕ#)−1.If 1X−γand 1X−δare invertible,thenf=ϕ+η−εhas the group inverse andf#=(1X−γ)−1αϕ#(1X−δ)−1. Corollary 17.10([14,Corollary3.3])LetJ(R)be Jacobson radical anda∈RwithaDexisting,j∈J(R).Ifj(aD a−1)a=0 anda(aD a−1)j=0,thena+j−εhas the Drazin inverse,whereε=(1−aaD)j(1+aD j)−1(1−aD a). Proof Sincej∈J(R),we have that 1+a#j,1−γand 1−δare invertible.From Theorem 17.8,the conclusion holds. Theorem 17.11 generalizes the conclusion in[6]to morphisms in an additive category. Theorem 17.11([14,Theorem3.4])LetCbe an additive category.Suppose thatϕ:X→Xis a morphism ofCwith the Drazin inverseϕDand thatη:X→Xis a morphism ofCsuch that 1X+ϕDηis invertible and Letf=ϕ+η.Then the following statements are equivalent: (1)fhas a Drazin inverse,andf D=(1X+ϕDη)−1ϕD. (2)ϕϕDηm=ηm,wheremis a positive integer. (3)ηmϕϕD=ηm,wheremis a positive integer. In this case,f f D=ϕϕD. ProofLet=(1X+ϕDη)−1ϕD.The proof is similar to Theorem 17.8,hence we have fromϕϕDη=ηϕDϕ,we have Then Similarly(1X−ϕDϕ)β−1=1X−ϕDϕ.Hence Since 1X−=1X−ϕDϕ,we have Similarly to the proof of Theorem 17.8,we have=f+(ϕϕDϕ−ϕ−ε),where From(17.88)and hypothesis,we haveϕη1X−ϕϕD=ηϕ1X−ϕϕD.By induction we have Next we prove In fact,by(17.88) It is easy to check(17.91)is true whens=1.Suppose that the conclusion holds ats,then Hence for arbitrarys,(17.91)holds.And we have Therefore (2)(3).It is easy to obtain by(17.92). (2)(1).If there exists a positive integerm≥1 such thatϕϕDηm=ηm,then SinceϕDis the Drazin inverse ofϕwith ind(ϕ)=k.Lets=m+k−1.Then we have Hence by(17.94),we have Thereforefhas the Drazin inverse with ind(f)≤sand.By(17.89),we havef f D=ϕϕD. (1)(2).Supposef D=(1X+ϕDη)−1ϕDis the Drazin inverse offwith ind(f)=s.AsϕDis the Drazin inverse ofϕwith ind(ϕ)=k.Let Thenus=0,vk=0,and by(17.89)we havef f D=ϕϕD, Then and we haveuv=v u.Letm=s+k−1.Then(u−v)m=0.But Note that(17.88),we haveη(1X−ϕϕD)=(1X−ϕϕD)η.Hence That is,there exists a positive integerm≥1 such thatηm(1X−ϕϕD)=0 andηm=ηmϕϕD. Theorem 17.12 generalizes the conclusion in[46]to morphisms in addition category. Theorem 17.12([14,Theorem3.5])LetCbe an additive category.Suppose thatϕ:X→Xis a morphism ofCwith the Drazin inverseϕDand thatη:X→Xis a morphism ofC.Then the following statements are equivalent: (1)ϕϕDη=ηϕϕD=ϕ−ϕ2ϕD+η. (2)f=ϕ+ηhas the group inverse andf#=(1X+ϕDη)−1ϕD. Proof(1)(2).Let.By the condition(1),we have Similarly,sinceη=ηϕDϕ+ϕ2ϕD−ϕ,we have=ϕDϕ.Hence Hence,f=is the group inverse off. andf#f=ϕDϕ. (2)(1).It is similar to the proof of Theorem 17.8,we have Multiply on the right side of(17.96)byϕD,we have that is Similarly,multiply on the left side of(17.96)byϕD,we have Then we obtainηϕD=ϕDϕηϕDandϕDη=ϕDηϕϕD.Therefore

11 Drazin Inverses in Semigroups or Rings











12 Drazin Invertibility in Two Semigroups of a Ring




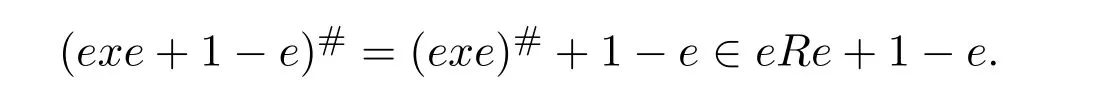



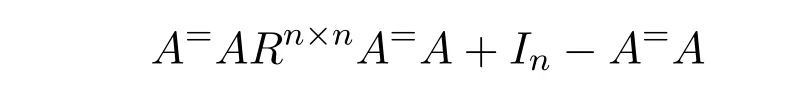
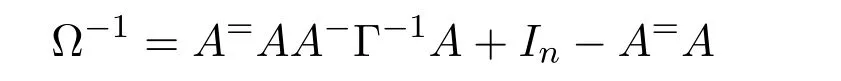











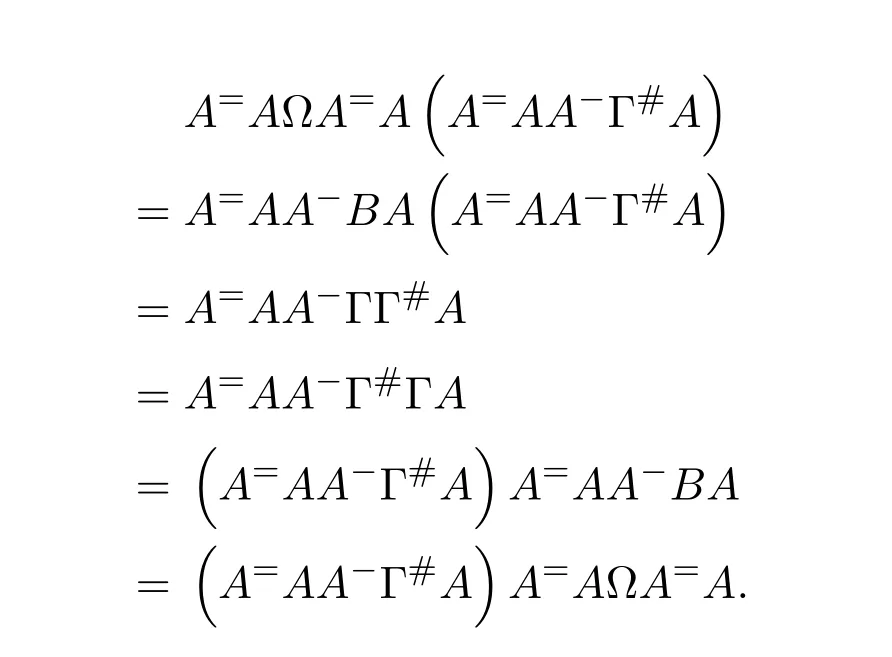










13 Jacobson’s Lemma and Cline’s Formula for Drazin Inverses






















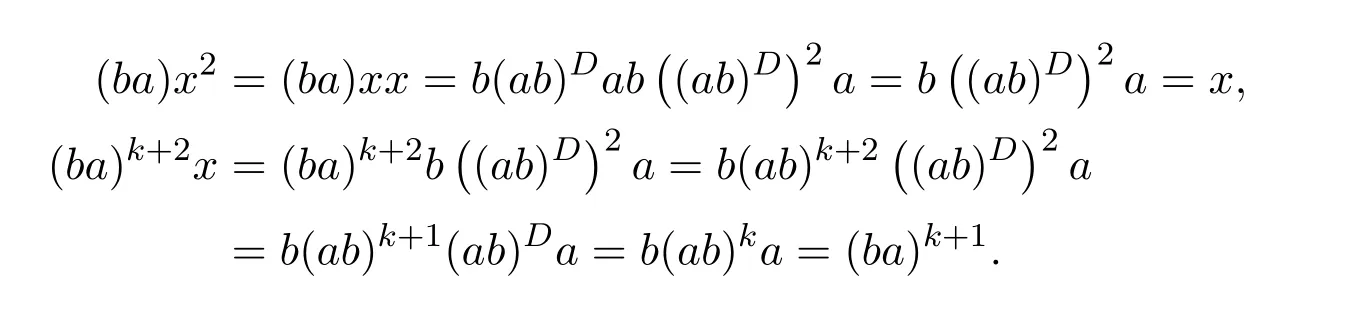
14 Additive Properties of Drazin Invertibility of Elements










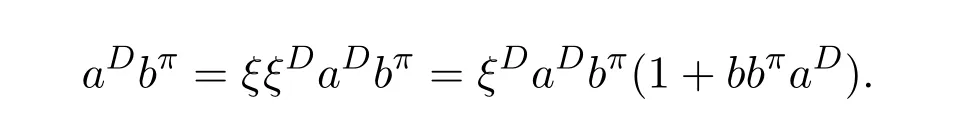










15 Drazin Invertibility of the Product and Difference of Idempotents











16 Drazin Invertibility for Matrices Over a Ring

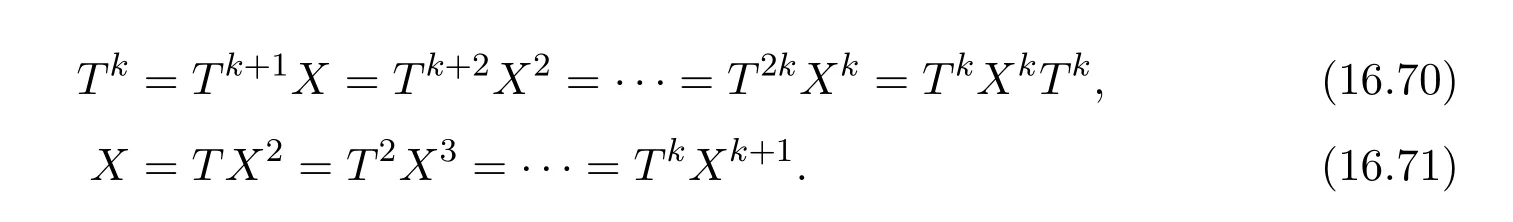





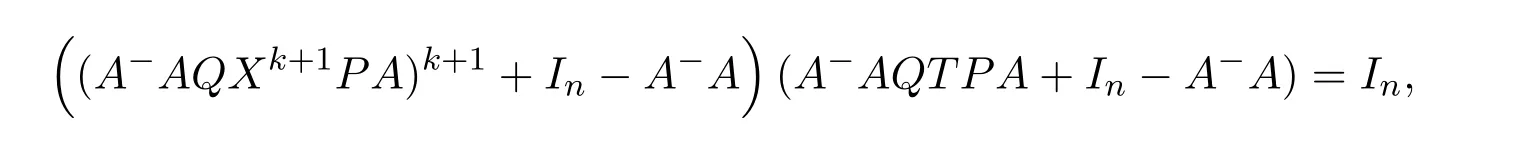








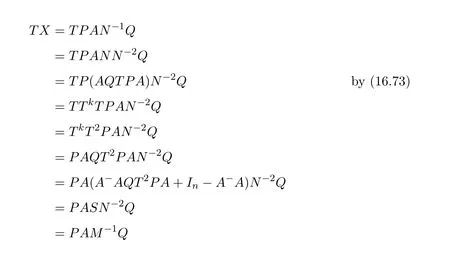
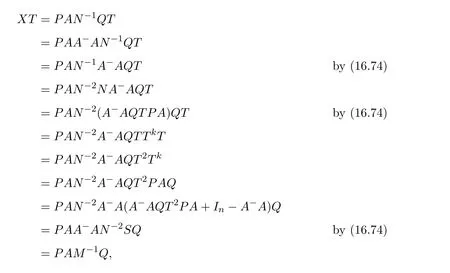

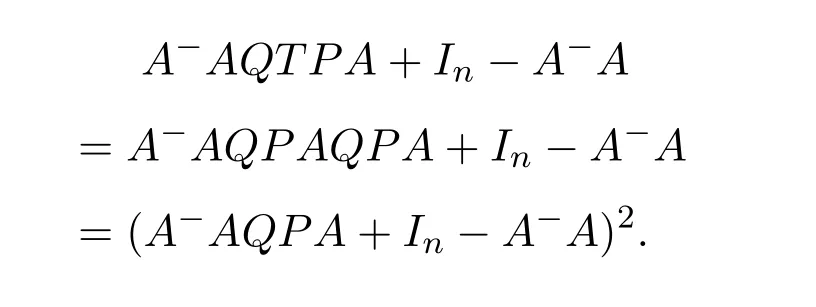





















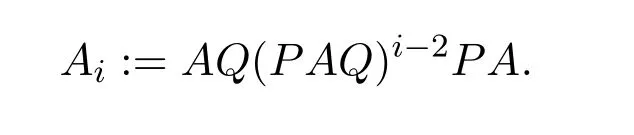






17 The Drazin Inverse of a Sum of Morphisms