一类PDE-ODE级联系统的指数镇定
孟玉翠
(山西大学数学科学学院,太原 030006)
近年来,常微分方程(ODE)-偏微分方程(PDE)级联系统的镇定问题越来越得到广大研究者的关注[1-7].它可以描述很多不同的物理问题,如交通流、化学反应器和热交换器等. 在文献[8]中,作者提出了利用偏微分方程backstepping方法来镇定一阶不稳定的双曲偏微分方程,该方法还应用到了具有执行器和传感器延迟的系统[9]. 文献[10]将时滞描述为一个传输方程,并考虑了一阶双曲偏微分方程和ODE级联系统的镇定问题. 关于偏微分方程backstepping方法的其他应用可以在文献[11-18]中找到. 虽然偏微分方程backstepping方法已经有效地解决了ODE-PDE级联系统的镇定问题,但backstepping方法的核函数通常是一个偏微分方程,从而相对复杂. 与此不同,本文设计了一个新的变换,其优点之一是核函数是一个常微分方程,其求解难度远比通常的backstepping方法核函数的求解小. 该方法的另一个优点是在证明闭环系统的稳定性时,避免了构造Lyapunov函数的困难.
考虑下面的系统:
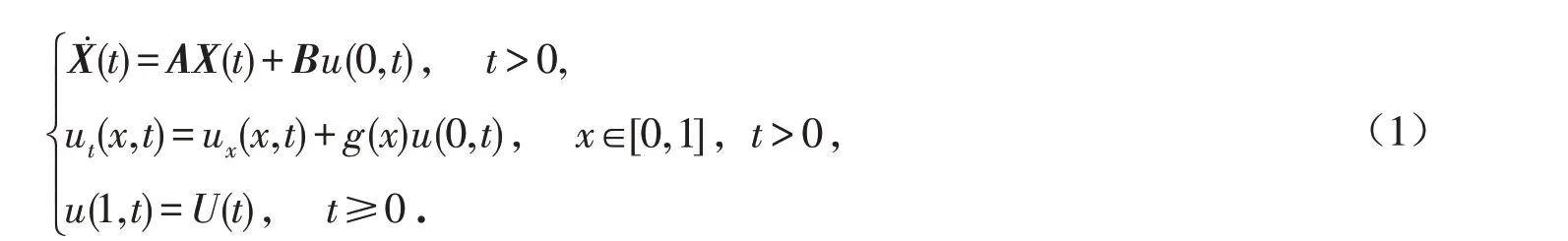
其中:X是ODE的状态;A∈ℝn×n;B∈ℝn×1;g∈C[0,1];U是控制. 在状态空间ℝn×L2(0,1)中考虑系(1),其内积定义为
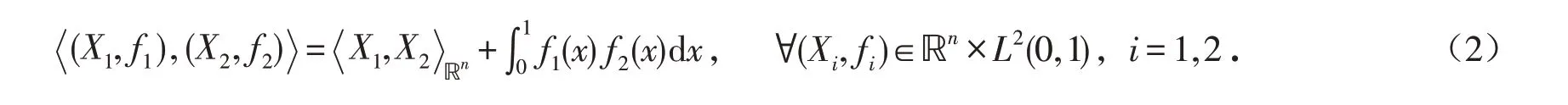
1 控制器的设计
我们将控制U(t)分为两部分

其中:U0(t)用来镇定一阶双曲偏微分方程;U1(t)是待定的新的控制. 按照文献[8],利用backstepping 方法,U0(t)可以设计如下:
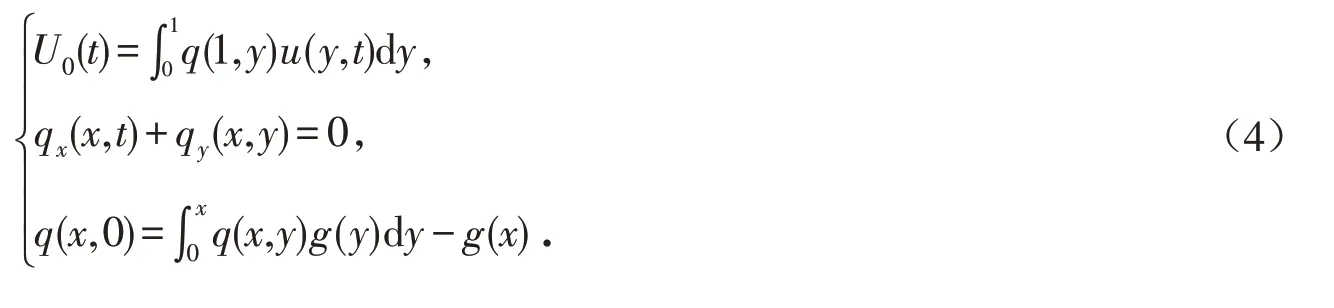
由式(3)和(4),系统(1)可以化为
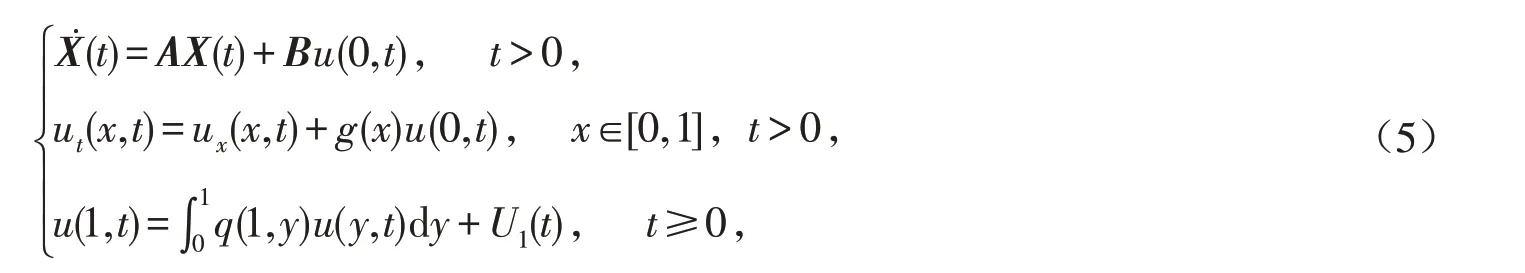
其中核函数q(x,y)是由式(4)给定的. 引入变换

对式(6)求导可得
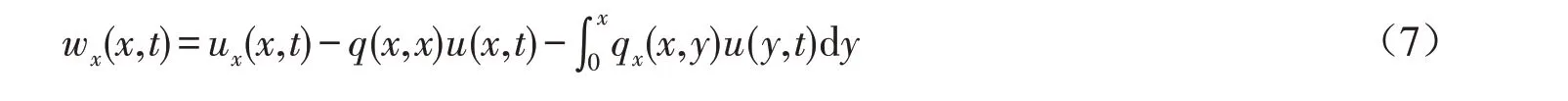
和
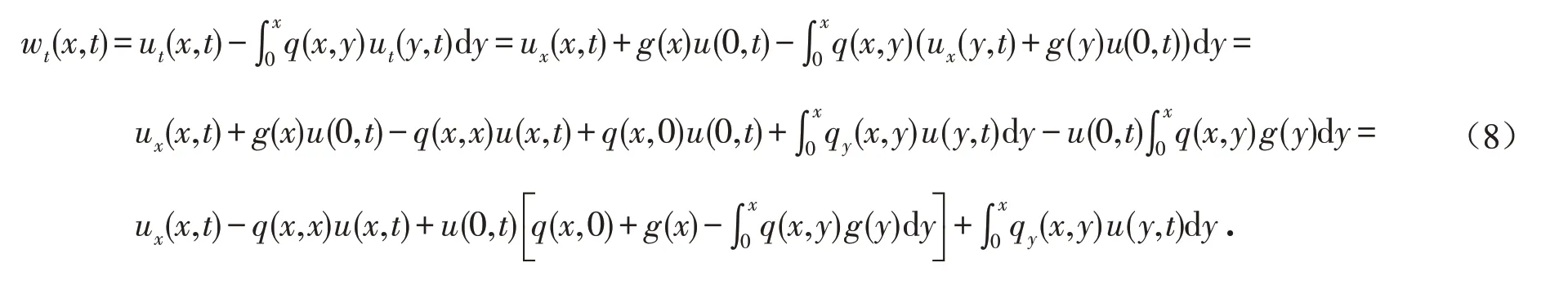
将上述两个等式相减,再根据式(4),可以将系统(5)转化为
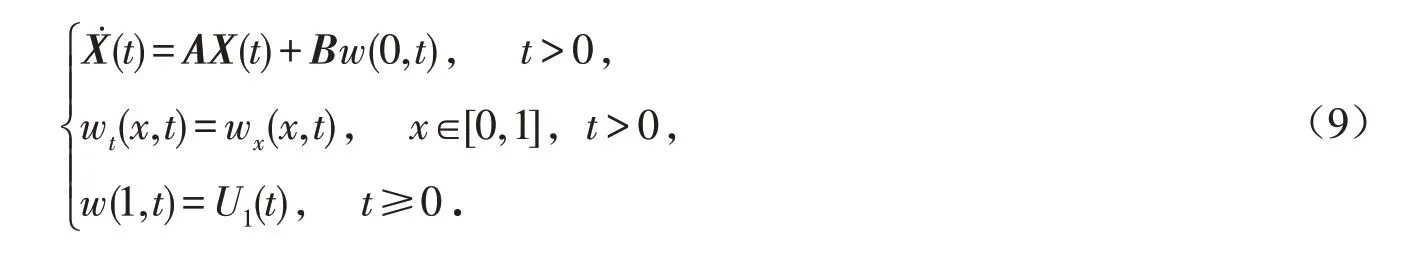
现在设计控制器U1(t)来镇定系统(9),受文献[19]的启发,引入如下变换:

其中H(x):[0 ,1] →ℝn是待定的向量值核函数. 显然变换式(10)是可逆的,其逆为

为了求解向量值核函数H(x),对X͂(t)求导可得:
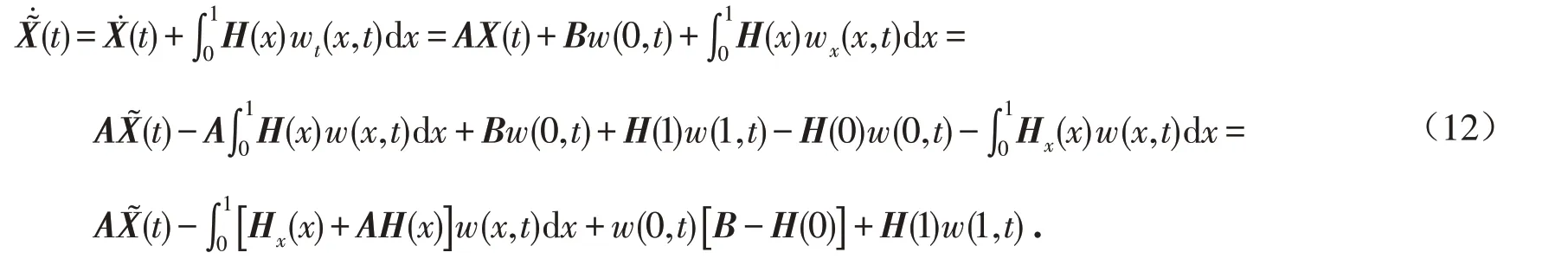
如果选择H(x)使得

则式(12)变为

解式(13)可得

因此

只需镇定系统(16)即可,根据极点配置定理

其中K使得矩阵A+e-ABK是Hurwitz矩阵. 在状态反馈(17)的条件下,我们得到闭环系统

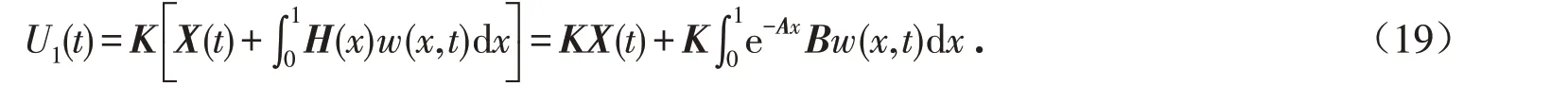
于是得到系统(1)的闭环系统
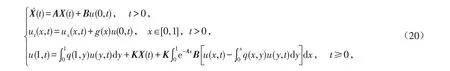
其中q(x,y)满足式(4).
定理1 令A∈ℝn×n,B∈ℝn×1,g∈C[0,1]. 假设(A,B)是可控的,σ(A)⊂{λ∈ℂ|Reλ≥0} ,则存在K∈ℝ1×n使得A+e-ABK是Hurwitz矩阵,并且对任意的初始状态(X(0),u(∙,0) )∈ℝn×L2(0,1),闭环系统(20)存在唯一解(X(t),u(∙,t) )∈C([ 0,∞);ℝn×L2(0,1)) ,并且存在常数ω>0,满足
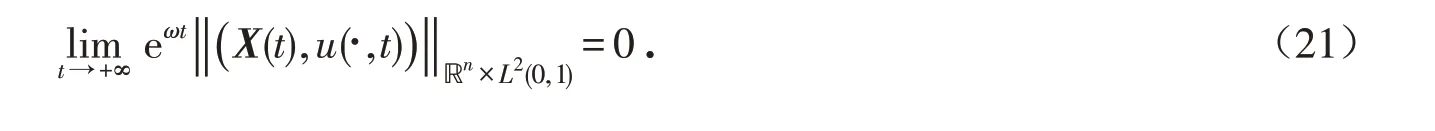
2 闭环系统的稳定性
本节分析闭环系统(20)的稳定性,为此先给出如下引理.

w-子系统是一个简单的传输方程,它的解可以被表示为

根据式(23)和(24)可知,随着时间t趋于无穷大,w(x,t)的解指数衰减到零,故w-系统也是指数稳定的.因此整个闭环系统(18)是指数稳定的. 证毕.
定理1的证明.因为(A,B)是可控的,根据极点配置定理可知存在矩阵K1∈ℝ1×n使得A+BK1是Hurwitz矩阵.由于eA[A+e-ABK1eA]e-A=A+BK1,A+e-ABK1eA是Hurwitz 矩阵当且仅当A+BK1是Hurwitz矩阵,故A+e-ABK1eA也是Hurwitz矩阵. 因此,我们可以选择K=K1eA.
根据文献[1]可知变换式(6)是可逆的,且其逆为

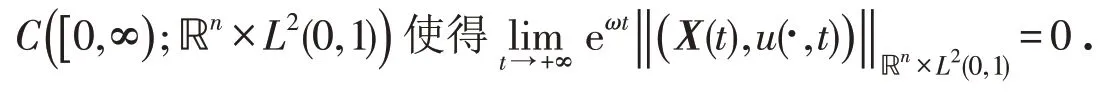
3 结论
本文提出了一种新方法来镇定由一阶双曲PDE 和ODE 组成的级联系统. 与传统的偏微分方程backstepping方法不同,所提新方法的一个优点为核函数是一个常微分方程,易于求解,从而简化了控制器的设计;另一个优点是在证明闭环系统的稳定性时,避免了构造Lyapunov函数的困难.

