二元双n次多项式插值问题研究
崔利宏, 聂碧宏, 李 雪
(辽宁师范大学 数学学院,辽宁 大连 116029)
多元函数插值与逼近是计算数学的一个重要研究方向.近年来,随着电子计算机运算以及处理能力的不断提升,多元函数插值在相关学科领域的应用也愈加广泛和深入,这使得对多元函数插值问题的研究也就显得愈加重要.目前,对多元分次插值的研究更是许多科研、实际生产等领域所涉猎的重要内容.例如:在解决弹性力学问题时采用的有限元法,在飞行器(飞机、载人飞船)、舰船、高铁、汽车等产品外形设计过程中的曲面拼接技术等.这些问题都与多元函数插值密切相关,而二元双n次多项式插值则是多元函数插值的一种特殊情形,目前,在计算力学研究领域有着广泛的应用.本文在以往学者对二元插值研究的基础上[1-5],结合多元函数插值与逼近的相关理论知识[6-8],进一步研究了二元双n次插值正则结点组的基本拓扑结构和几何特征,得到了构造二元双n次插值多项式空间及沿二元双n次代数曲线插值正则结点组的构造方法.最后给出两个实验算例检验本文研究结果.通过应用Matlab软件编程,得到了被插值函数和插值函数在同一坐标系下的图像,进而明显地看出了插值与逼近的效果,同时给出了误差估计.
1 基本概念及主要定理


p(Qi)=fi,i=1,2,…d.
(1)
下面给出二元双n次插值空间的基本概念和二元双n次多项式插值的基本定义.

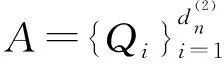
(2)
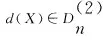

(3)

(4)
本文主要结果如下:
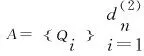

2 定理的证明
为了证明上述定理,需要如下基本引理.
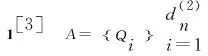

g(Qi)=0,∀Qi∈A
(5)
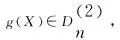
g(X)=q(X)·r(X).
(6)
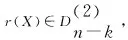
证引理的充分性是显然的,只需证引理的必要性即可.

又因为g(Qi)=0,∀Qi∈A,由定义4知,沿曲线q(X)=0恒有g(X)=0.则V(I1)⊂V(I2),I(V(I1))⊃I(V(I2)).
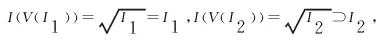
定理1的证明插值结点组C中所包含的点数为
(n+1)2+[(n+k+1)2-(n+k+1-k)2]=(n+k+1)2,

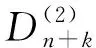
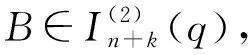
dn+k(X)=q(X)·r(X).
(7)
因为dn+k(Qi)=0,∀Qi∈A,所以0=dn+k(Qi)=q(Qi)·r(Qi),∀Qi∈A.但是q(Qi)≠0,∀Qi∈A.所以只有r(Qi)=0,∀Qi∈A.

故有r(X)≡0,进而dn+k(X)≡0,这与假设矛盾.定理1证毕.
定理2的证明插值结点组A∪B中所含的点数为
2mk+[(n+1)2-(n+1-k)2]=(n+m+1)2-(n+m+1-k)2,


g(X)=α(X)p(X)+β(X)q(X).
(8)

又因为
g(Qi)=0,∀Qi∈A,
(9)
将式(9)代入式(8)中有α(Qi)p(Qi)=0,∀Qi∈A.而p(Qi)≠0,∀Qi∈A.故只有α(Qi)=0,∀Qi∈A.


(10)
将式(10)代入式(8)中有g(X)=q(X)·r(X).证毕.
3 实验算例
设被插值函数为f(x,y)=2x+y,取点Q1(0,0)∈2,则不经过Q1(0,0)在直线y=x-1上任取3个点Q2(0,-1),Q3(1,0),Q4(2,1),根据定理1,这4个点构成二元双一次空间的正则结点组,且所确定的唯一一条插值函数为
d1(x,y)=1+x+0.5y+2.25xy.
由Matlab做出被插值函数f(x,y)和插值函数d1(x,y)的图像如图1所示.
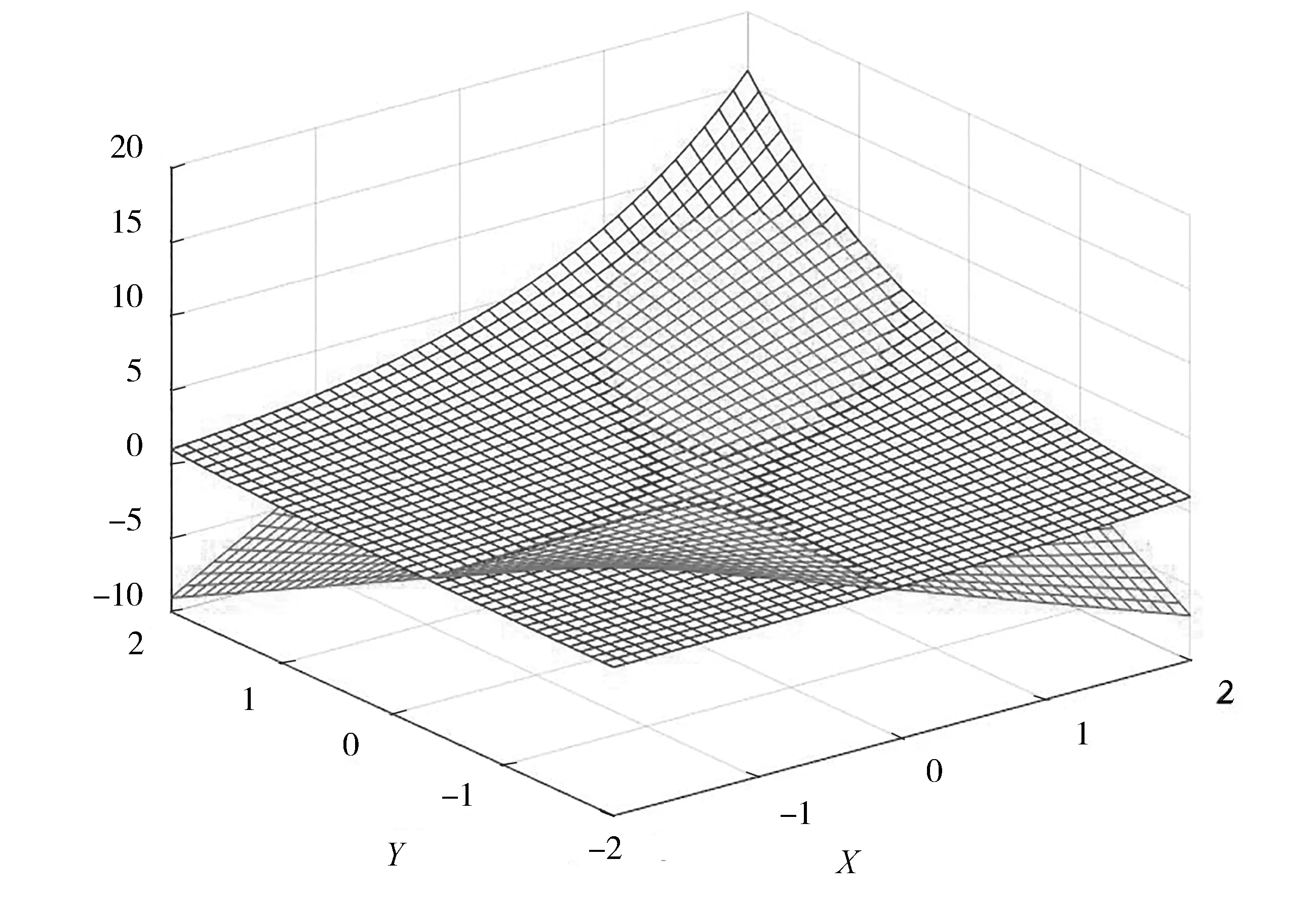
图1 二元双一次插值效果图Fig.1 Binary double linear function interpolation rendering

由Matlab做出被插值函数f(x,y)和插值函数d2(x,y)的图像如图2所示.
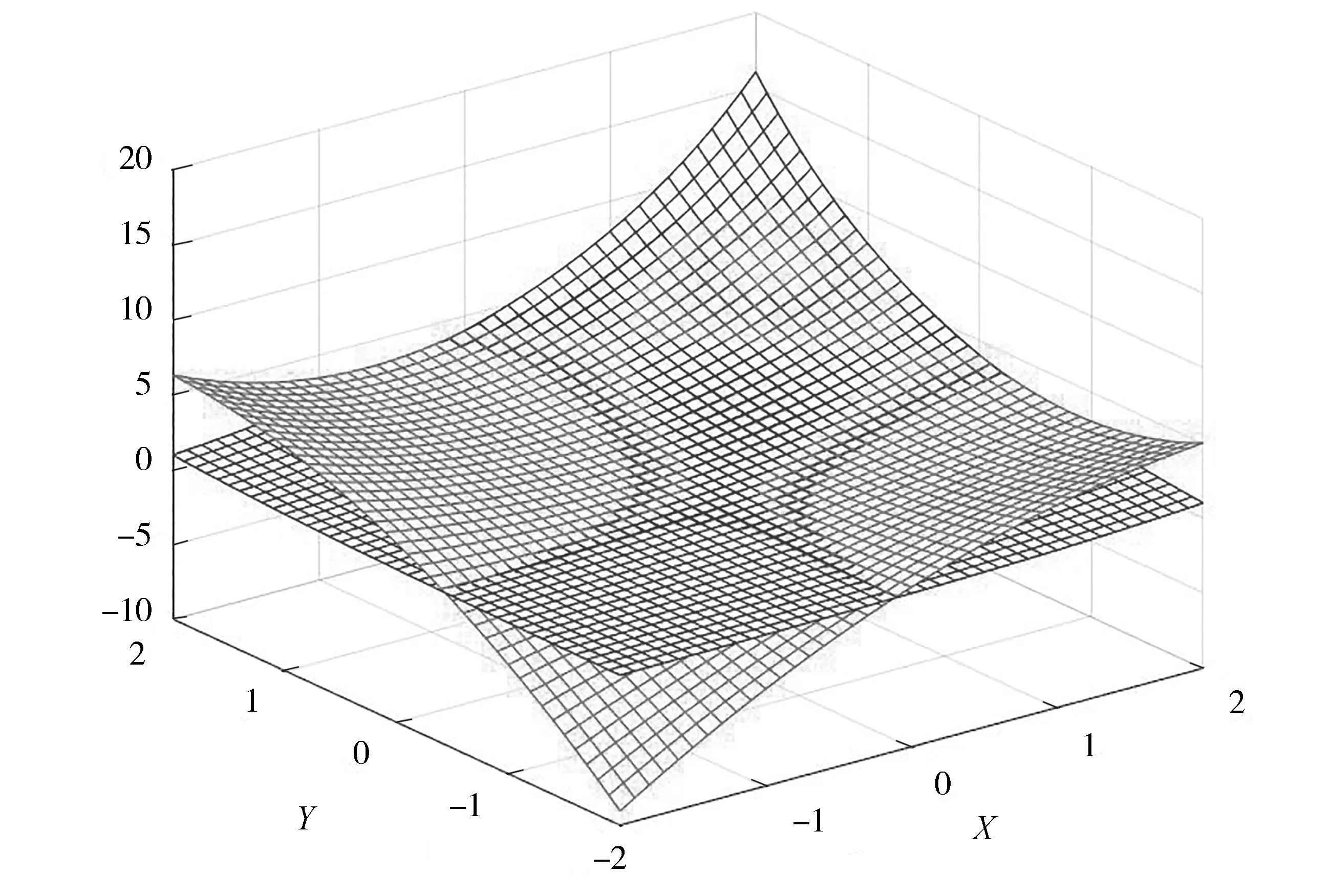
图2 二元双二次插值效果图Fig.2 Binary double quadratic interpolation rendering
下面对二元双一次插值多项式和二元双二次插值多项式的插值逼近效果进行分析.
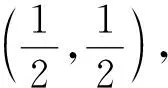
因此求得两个算例的绝对误差和相对误差分别为
r1=|2-2.312 5|=0.312 5,r2=|2-1.937 5|=0.062 5,
通过以上数据,发现插值函数的次数越高,插值函数越逼近被插值函数,即插值的效果越好.

