Memory-augmented adaptive flocking control for multi-agent systems subject to uncertain external disturbances
Ximing Wang(王希铭), Jinsheng Sun(孙金生), Zhitao Li(李志韬), and Zixing Wu(吴梓杏)
School of Automation,Nanjing University of Science and Technology,Nanjing 210094,China
This paper presents a novel flocking algorithm based on a memory-enhanced disturbance observer.To compensate for external disturbances,a filtered regressor for the double integrator model subject to external disturbances is designed to extract the disturbance information.With the filtered regressor method,the algorithm has the advantage of eliminating the need for acceleration information, thus reducing the sensor requirements in applications.Using the information obtained from the filtered regressor,a batch of stored data is used to design an adaptive disturbance observer,ensuring that the estimated values of the parameters of the disturbance system equation and the initial value converge to their actual values.The result is that the flocking algorithm can compensate for external disturbances and drive agents to achieve the desired collective behavior,including virtual leader tracking,inter-distance keeping,and collision avoidance.Numerical simulations verify the effectiveness of the algorithm proposed in the present study.
Keywords: flocking control,multi-agent systems,adaptive control,disturbance rejection
1.Introduction
Cooperative control of multi-agent systems has been a hot topic in the field of control theory and applications.Cooperative control deals with the problem of controlling a multiagent system to fulfill a common goal, such as consensus control,[1–3]formation control,[4–7]containment control,[8–10]and flocking control.[11–13]The common advantage of these algorithms is the theoretical and practical value of using local information in the system to achieve the desired collective motion,thereby reducing costs and improving robustness.
Inspired by biological systems, flocking control focuses on the collective motion of multi-agent systems in which each agent has a limited communication distance, with applications ranging from swarm of unmanned aircraft vehicle(UAV) drones robots[14]to mobile sensor networks.[15]The core advantage of flocking control is that it guarantees collision avoidance, lattice-like formation, leader-tracking, connectivity preservation at the same time.However, most existing flocking algorithms, e.g., in Refs.[16–23], do not take into account the presence of external disturbances in a system, which makes them unsuitable for applications with high robustness requirements.
External disturbances can negatively affect the system,including degrading the performance,preventing the control system from converging to the desired state,or causing agents to collide.Therefore,disturbance rejection is an important practical issue confronting flocking applications.In the existing literature, disturbance-rejection flocking algorithms, e.g., in Refs.[24–26], utilize different control techniques to stabilize the flocking systems.In Ref.[24],the authors took advantage of the sliding mode control to compensate for bounded external disturbances.The advantage of sliding mode control is that once knowledge of the upper bound on the disturbance is obtained,the disturbance can be compensated for by setting a sufficiently large sliding mode gain.However,large gains require very high control frequencies,which impose significant costs on the application and inevitably cause chattering as a side effect.In Ref.[25],the authors proposed a flocking algorithm based on a full-order disturbance observer to compensate for matched and unmatched modelable disturbances.The benefit of this approach is that it enables the controller to compensate for external disturbances in general,both bounded and unbounded.However,this approach requires the controller to have precise prior knowledge of the form of the disturbance equation,which is difficult to obtain in practice.In Ref.[26],the authors designed a flocking controller using multiple adaptive gains for linear models with time-varying uncertainties and external disturbances.The highlight of this method is that it uses continuous inputs to compensate for unknown bounded perturbations by setting exponential adaptive gains.However,the adaptive gains induce two negative effects.One is that the exponential form of the gains is likely to be too large,making it difficult to apply, and the second is that the algorithm does not make the positions of the agents converge to a configuration that is a minimum of the potential energy field and thus does not guarantee that the formation will be as expected.
It can be seen that the existing disturbance-rejection flocking algorithms in the literature have different shortcomings, and it is necessary to develop a disturbance-rejection flocking control algorithm with continuous input and a low requirement for a priori knowledge of external disturbances.Inspired by the filtered regressor,[27–29]in this study we propose a novel disturbance-rejection flocking algorithm using adaptive disturbance observers,where each agent can estimate the disturbance without knowing the parameters of the external disturbance system equation or the initial value of the disturbance, thus allowing the agents to compensate for the external disturbance without chattering.In addition, we also use recorded data to further improve the performance of the disturbance observer.
We summarize the contributions of this paper as follows:(1) A disturbance-rejection flocking algorithm is proposed to use an adaptive control method for the first time.Compared to the existing disturbance-rejection flocking algorithms, our proposed algorithm does not require knowledge of the parameters of the external disturbance system equation.To achieve this goal,we propose a new disturbance observer that uses the filtered regression approach to decompose the external disturbance into the product of a known regression matrix and an unknown constant parameter vector.(2)It is remarkable that the proposed flocking algorithm uses the recorded data to guarantee that the disturbance estimation given by the observer converges to the actual value of the disturbance.In classic adaptive control systems,the convergence of the estimated parameters depends on whether the regression matrix satisfies the persistent excitation(PE)condition.When the PE condition is not satisfied,adaptive control can not guarantee the parameters to converge to the actual values,resulting in degraded performance.In this paper, a new adaptive law based on a filtered regressor is designed,in which the estimated disturbances converge to the actual disturbances as well as stabilize the system if only the recorded data satisfy the full rank condition.
The rest of this paper is organized as follows: In Section 2 we provide the basics of system models, assumptions, and the virtual potential functions for flocking control.In Section 3 we introduce the novel disturbance observer for the doubleintegrator dynamics using filtered regressors.In Section 4 we give the flocking algorithm and its theoretical analysis.In Section 5 we verify the effectiveness of the proposed algorithm through a numerical simulation.Finally,in Section 6 we give some conclusions and future perspectives.
2.Preliminaries
2.1.System model
Consider a multi-agent system consisting ofNdoubleintegrator particles,which can be expressed by

whereqi(t) ∈Rn, ˙qi(t) ∈Rnand ¨q(t) ∈Rnare the position, velocity, and acceleration of theith agent, respectively;di(t)∈Rnis the external disturbance,and τi∈Rnis the control input of theith agent.Furthermore,we assume that there exists a virtual leader in the system.The leader’s positionq0and velocity ˙q0are smooth enough so that ¨q0exists and is continuous.Next, we assume that the disturbancedican be expressed as
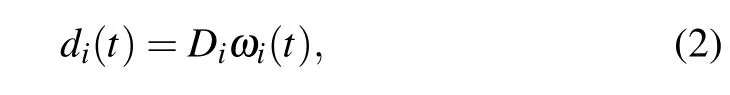
whereDi∈Rn×mis an unknown matrix satisfying rank(Di)=m,ωi∈Rm×1and

withAi∈Rm×mbeing an unknown matrix.Therefore, each disturbancedican be captured if the unknown parametersDi,Aiand the initial value ωi(t0)are estimated.Note that by the assumption ofDi,there exists a Moore–Penrose pseudoinversesuch that=Im.
2.2.Communication topology
The proximity-induced topology[30,31]is employed to describe the information flow in system (1).Consider an undirected graph G = (V,E,A), where elements in vertex set V ≜{1,...,N}index agents,edge set E ≜{(i,j)|i,j∈V,‖qi−qj‖≤r} represents the communication links between neighboring agents,and A=[aij]∈Rn×nis the weight matrix with eachaij∈[0,1].Note thataij=aji∀(i,j)∈[1,N],andaij=0 if(i,j) /∈E.Here,the constantr>0 is known as the maximal communication radius.Thejthagent is called a neighbor of theith agent and vice versa if(i,j)∈E,and the neighborhood set ofican be defined as Ni≜{j|(i,j)∈E}.
2.3.Virtual potential field functions
Following the approach in Ref.[30], a bump function ρh:R≥0→[0,1] is needed to construct the virtual potential field function as well as the weights in the communication topology.Since all existing bump functions to our knowledge are not twice differentiable and the algorithm proposed in this paper will use the twice differentiable of the potential field function to stable the flocking system,we propose a new bump function ρhas follows:

where constanth∈(0,1).Hence,the weights in G can be defined asaij=.Similar to Ref.[30],we define the virtual potential field function using the integral of the product of bump function (4) and a continuous differential action function φ :R≥0→R which satisfies

wherelais the expected inter-distance of neighboring agents.Then, the virtual potential field function ψ :R≥0→R≥0can be defined as

Hence, the virtual potential field function between agentiand agentjis given byand the corresponding interaction is denoted by φi j=∇qi−q jψij.Note that since the bump function (4) is twice differentiable,is continuous.The positivity of ψ can be obtained by checking its minimal value.Based on the definition, ψ decreases monotonically inand increases monotonically in.Therefore, ψ reaches its minimal value atz=, resulting in ψ ≥= 0.Similarly, to track the virtual leader, the leader’s potential field function ψd:R≥0→R≥0is defined as
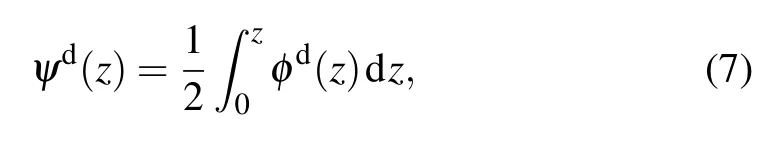
where φd(z) is a positive continuously differential function and φd(‖z‖2)=0 if and only ifz=0.For convenient, the virtual potential field function between agentiand the virtual leader is given byand the corresponding interaction is denoted by.
3.Disturbances observer
3.1.Filtered regressors
The double-integrator dynamics in Eq.(1) can be developed as
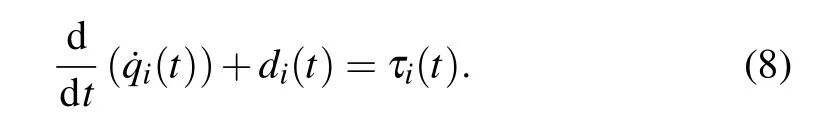
Then,the following lemma is used to introduce the filtered regressor.
Lemma 1The following equation holds:
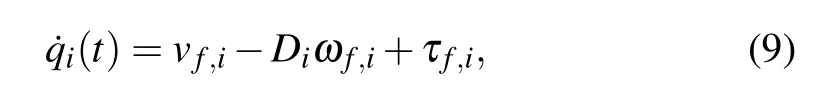
where

with any appropriate positive constantai.
ProofEquations(10)–(12)can be expressed in the form of convolution as


Then,using integration by parts we have
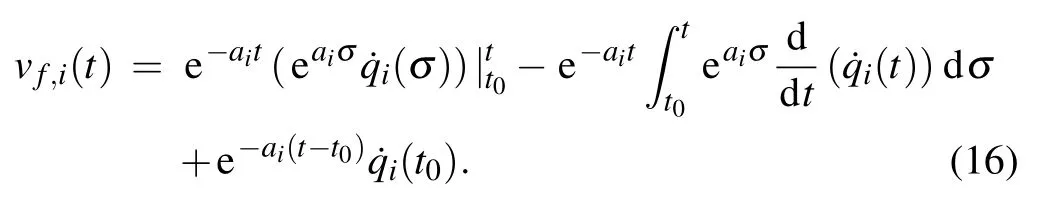
Substituting Eq.(8)into Eq.(16),we can continuously get
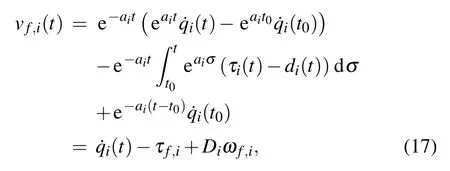
which completes the proof.
Remark 1From Lemma 1, it can be seen that signalDiωf,ican be captured using measurable signalsand τf,i.
Similarly, the filtered regression can also be applied for external system(3).
Lemma 2The following equation holds:
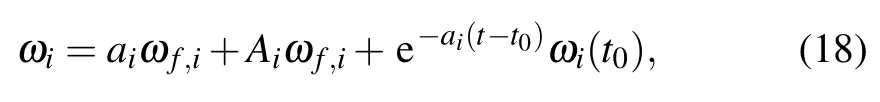
where ωf,iis defined in Eq.(11).
ProofUsing integration by parts for Eq.(14),we have
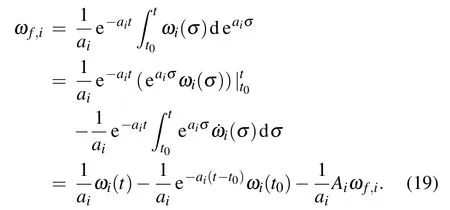
Then,multiplyingaiat its both side,it follows that
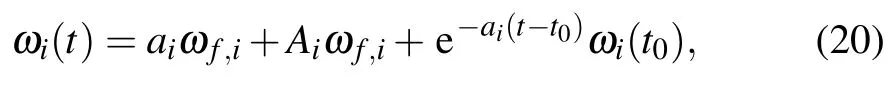
which completes the proof.
3.2.Disturbance observer
Using Eq.(18)and noting that=Im,one obtains


4.Observer-based flocking algorithm
4.1.Controller design
For convenience, let us define position, velocity and coordination error signals as
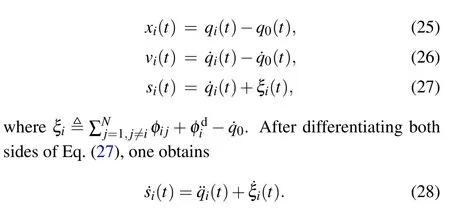
Substituting Eqs.(27)and(28)into Eq.(1)yields

Then,we give the control input τias
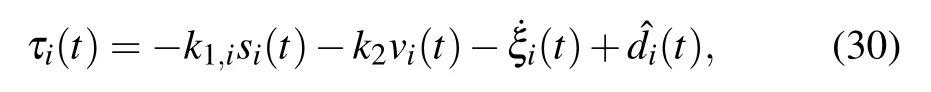
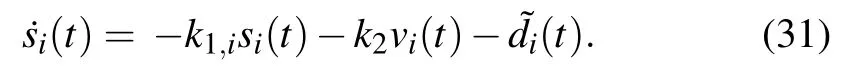
Next,substituting Eq.(24)into Eq.(31)yields
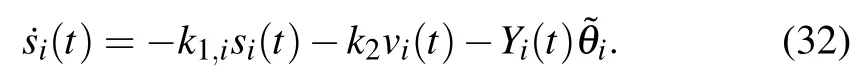
Now,we are ready to give the adaptive laws for ˆAiand ˆω0,iin a compact form as

where Γiis a positive matrix, and data (Yi(t),Wi(t)) are defined as


whereYiis defined as in Eq.(23),τf,iis defined as in Eq.(12),vf,iis defined as in Eq.(10), constant δi> 0, andMi={ti,1,...ti,m}is a set contains time instants when the data pair(Yi(t),Wi(t))is recorded.Here,we assume that the data pairs are sufficiently recorded such that the following assumption holds.
Assumption 1For each agenti, the data pairs(Yi(t),Wi(t)) are sufficiently collected in a finite duration such that there exits a constant βi>0 satisfying

where λmin(z) means the minimal eigenvalue of matrixzand Yi=.
Remark 2Following Ref.[32],assumption 1 can be verified online during the collection and once Yiis full rank,the data collection process can be stopped.Note that we can select a larger βito guarantee a better convergence rate of the estimated parameters.Moreover, real-time applicability is an issue that needs to be considered in applications.Since the amount of data to be gathered in the proposed algorithm is hard to determine beforehand,the amount of computation required by the flocking algorithm increases in the event of too much data being collected.For this reason,data selection can help to improve the real-time performance of the system.See Ref.[33]for more information.
4.2.System analysis
Consider a Lyapunov function as

where
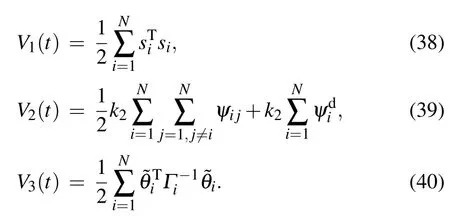
Then,we have the following theorem.
Theorem 1Consider a multi-agent system(1)applying flocking controller (30) with disturbance observer consisting of Eqs.(23) and (33).Then, ifV(t0) is limited and assumption 1 is satisfied,the following statements holds:
(2)(Formation)q=converges to an equilibrium point that is a local minima ofV2.
(3)(Disturbance observation)→di(t)ast→∞.
(4) (Collision avoidance) GivenV(t0) < (k+1)ψ(0).Then,at mostkdistinct pair of agent could possibly collide.
ProofDifferentiating both sides ofV1,we have

Substituting Eq.(32)into Eq.(41)yields

Hence,it follows that

Differentiating both sides ofV2,we have

Differentiating both sides ofV3and using Eq.(33), one can obtain

Next,substituting Eq.(22)into Eq.(8),we have
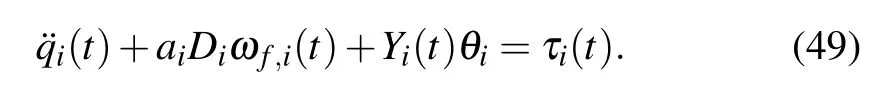
After substituting Eq.(9) into Eq.(49), we can continuously obtain

which yields
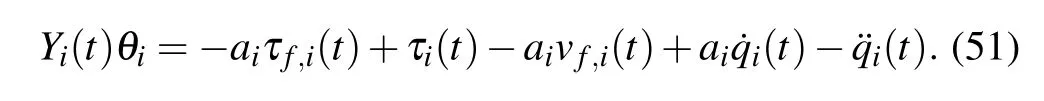
Then,using Eqs.(12)and(10),we can continuously reach

Next,integrating both sides of Eq.(52),one obtains
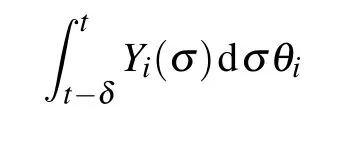
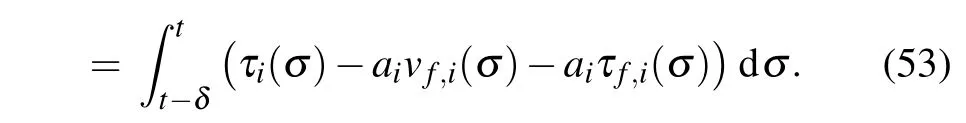
Therefore,we have

Now,substituting Eq.(54)into Eq.(48),we can obtain

Then,after merging Eqs.(45),(46)and(55),the derivative of Eq.(37)is calculated as
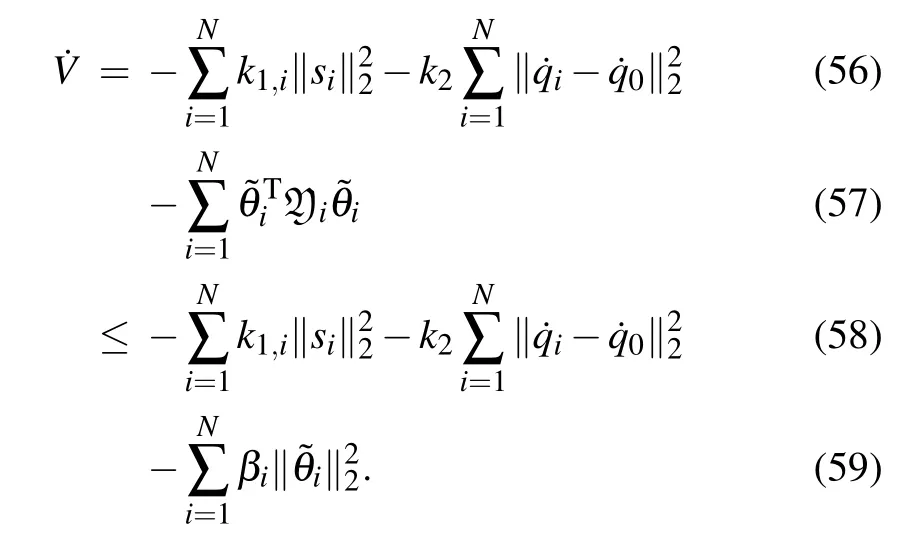
Using LaSalle’s invariant set principle, all solutions stared fromasymptotically converge to the largest invariant set contained in

5.Numerical study
Flocking control originates from imitations of biological imitation in nature, and therefore numerical simulation of flocking systems has been an important research method.In the early days, the Boids model[34]based on heuristic rules was proposed in order to graphically implement the imitation of bird flocks.Subsequently, Vicseket al.[35]and Couzinet al.[36]proposed mathematical models of flocking that focus on revealing the behavior in complex systems.To facilitate the theoretical analysis of the behaviors of flocking systems, models such as Cucker–Smale’s model[37]and Olfati’s model[30]have been proposed, which model the agents as double-integrator,reducing the difficulty of analyzing flocking systems using stability theory and thus obtaining the theoretical conditions for velocity consensus,collision avoidance,and so on.The double-integrator model is a highly abstract model that uses only the position and velocity of a agent as states and the acceleration as control input.Therefore, this class of flocking algorithms is suitable for applications in multi-robot systems with inertia, such as quadrotor swarms[38]and autonomous surface vehicles.[39]
To show the control effect of the proposed algorithm,let us consider the double-integrator multi-agent system(1)consisting of 10 agents with a prescribed trajectoryq0(t)designed as

The initial positions and velocities of all agents are randomly selected in[−5,5].The communication radiusr=1.2 and the expected inter-distancela=1.The initial values of disturbances are randomly selected in[−3,3],andAiis randomly generated such thatAi=−ATi,andDi=Infor all agents.The parameter of the smooth bump function ρhis set ash=0.9.The continuous differential action function φ is designed as

and the leader’s potential field function is designed as

In the filtered regressors(9),we setai=1 for all agents.In the controller(30),we setk1,i=1 andk2=1 for all agents.The simulation starts att0=0 and ends att=30,and data defined in Eq.(33)is collected every 0.3 s.
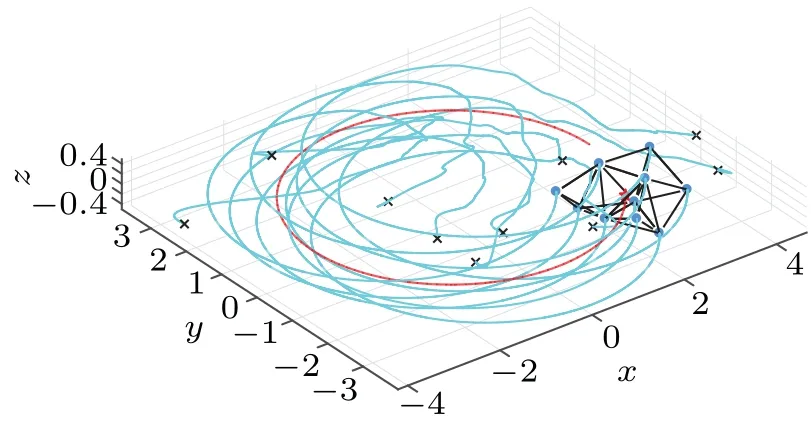
Fig.1.Flocking trajectories of all agents.

Fig.2.Velocity consensus of all agents.
As shown in Fig.1, all agents track the virtual leader while maintaining inter-distance without collision, where crosses, dots and lines denote the initial positions, final positions and trajectories of agents,respectively;the crosses and dashed line represent the position and trajectory of the virtual leader.The velocity differences between agents and the virtual leader are plotted in Fig.2,where all agents reach velocity consensus after 5 s.Figure 3 illustrates the convergence of the estimated parameters.Figure 4 shows that the disturbances estimated by all observers converge to the actual disturbances.Furthermore, as shown in Fig.5, no collisions occur during the simulation,and minimum inter-distances of all agents are close tola=1,as is expected.

Fig.3.Parameter convergence of all agents.

Fig.4.Disturbance observation errors.
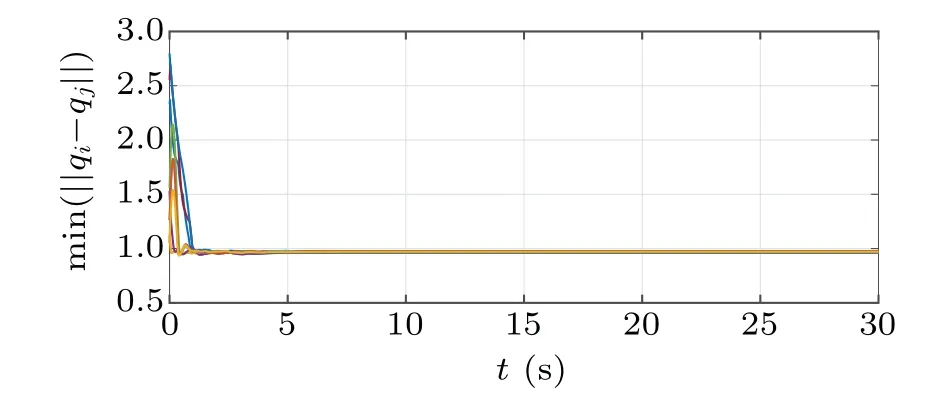
Fig.5.Minimum inter-distances of all agents.
6.Conclusion
A novel flocking algorithm using adaptive disturbance observer is proposed.Based on the designed filtered regressor, the disturbance observer estimates the disturbances in a way without the need of the acceleration information.The concurrent learning adaptive control method is employed to guarantee the convergence of the estimated disturbances, and LaSalle’s invariant set principle is used to guarantee the stability as well as collision avoidance and velocity consensus.Numerical simulation shows the perfect performance of the proposed algorithm.
Data Availability StatementThe latest source code is available at https://doi.org/10.5281/zenodo.5813300
- Chinese Physics B的其它文章
- High sensitivity plasmonic temperature sensor based on a side-polished photonic crystal fiber
- Digital synthesis of programmable photonic integrated circuits
- Non-Rayleigh photon statistics of superbunching pseudothermal light
- Refractive index sensing of double Fano resonance excited by nano-cube array coupled with multilayer all-dielectric film
- A novel polarization converter based on the band-stop frequency selective surface
- Effects of pulse energy ratios on plasma characteristics of dual-pulse fiber-optic laser-induced breakdown spectroscopy