正方形中“半角模型”热点试题赏析与思考
——从2021无锡中考试题第28题谈起

江苏省无锡市港下中学 程 军 （邮编：214199）

1 真题回放

（2021无锡中考压轴题第28题）已知四边形ABCD是边长为1的正方形，点E是射线BC上的动点，以AE为直角边在直线BC的上方作等腰直角三角形AEF，∠AEF＝90°，设BE＝m.

备用图

（1）如图1，若点E在线段BC上运动，EF交CD于点P，AF交CD于点Q，连结CF，

图1

②在△PQE中，设边QE上的高为h，请用含m的代数式表示h，并求h的最大值；

（2）省略.

解析（1）①由△AEF为等腰直角三角形，构图K字型（图2），过F作FG⊥BC，易知△ABE≌△EGF，FG＝BE＝CG＝，得CF＝

图2

对于（1）②，根据∠EAF＝45°，若能识别出这是正方形中的“半角模型”，则解题自然快捷简单.由正方形半角模型知，AE平分∠BEQ（图3），则∠AEB＝∠AEQ，由于∠AEF＝90°，则易知EF平分∠CEQ，故QE上的高h＝PH＝PC，由

图3

h＝时，h最大值

反思 本题第②题若看不出正方形中的半角模型，即AE平分∠BEQ，那么求h要困难些.

2 何为半角模型？

“半角模型”，就是指一个角包含着它的一半大小的角，且这两个角的顶点重合，把这种模型叫半角模型.当其中一个角为45°，另一个角为90°时，就称为正方形半角模型.

如下图，正方形ABCD中，∠EAQ＝45°＝∠BAD，一般有以下结论：

（1）EQ＝BE+DQ，（2）△CEQ周长＝2AB，（3）∠1＝∠2，∠3＝∠4，（如图4）

图4

证明，可通过旋转法完成，如图5，把△ADQ绕A顺时针旋转 90°到△ABQ′处，证△AEQ′≌△AEQ，得Q′E＝QE，∠1＝∠2，∠3＝∠4.

图5

正方形中半角模型应用十分广泛，现以2021全国中考试题为例，与读者分享.

3 正方形半角模型在中考试题中的应用和解析

例1（2021黄石） 如图6，在正方形ABCD中，点E、F分别在边BC、CD上，且∠EAF＝45°，AE交BD于M点，AF交BD于N点.

图6

（1）若正方形的边长为2，则△CEF的周长是______.

（2）下列结论：①BM2+DN2＝MN2；②若F是CD的中点，则tan∠AEF＝2；③连接MF，则△AMF为等腰直角三角形.其中正确结论的序号是 ____（把你认为所有正确的都填上）.

解析显然符合正方形半角模型，（1）△CEF周长＝2AB＝4，（2）如图7，把△ABM绕A逆时针旋转 90°，得△AM′D，由△AMN≌△AM′N，结合∠M′DN＝90°，即证BM2+DN2＝MN2.

图7

①正确；②由半角模型知∠AEF＝∠AEB（如图8），设DF＝CF＝x，EF＝y，由EF＝DF+BE，得BE＝y-x，CE＝2x-（y-x）＝3x-y，由勾 股 定 理 ，得，故tan∠AEF＝3，②错误.对于③利用△AMN∽△DFN（如图9），得△AND∽△MNF，∠MFN＝∠AND＝45°故③正确，正确序号为_①③.

图8

图9

反思本试题中用到两个常用结论，（1）△CEF周长＝正方形边长2倍，（2）EF＝BE+DF.

例2（2021葫芦岛） 如图10，将正方形纸片ABCD沿PQ折叠，使点C的对称点E落在AB上，点D的对称点为F，EF交AD于点G，连接CG交PQ于H，连接CE，下列四个结论中：

图10

（1）△PBE∽△QFG；

（2）S△CEG＝S△CBE+S四边形CDQH；

（3）EC平分∠BEG；

（4）EG2-CH2＝GQ·GD，正确的是_____（填序号即可）.

图12

解析（1）根据轴对称变换，易知∠CEF＝∠GFQ＝90°，利用K字型和“8”字型（如图11），

图11

得△PBE∽△EAG∽△QFG.（1）正确.（2）由折叠知（如图11），∠1＝∠DCE＝∠BEC，作CK⊥EF，△BEC≌KEC，△CKG≌△CDG，问题就又转化为正方形中的半角模型，即∠ECG＝45°，显然S△CEG＞S△CBE+S四边形CDQH，（2）错误.（3）正确.对于（4）连NH（如图12），则△CHN与例1中的△ANF是同一性质的等腰直角三角形，实质一回事.NH＝CH，则EG2-CH2＝GH2，即证GH2＝GQ·GD，也即证△GHQ∽△GDH，只要∠1＝∠GHQ＝45°，只要说明DH平分∠ADC（即B、D、H三点共线），作HS⊥AD，HT⊥CD，构图K字型，△PRH≌△HTC，故HR＝TC，HT＝HS，即∠1＝45°.故（4）正确，（如图13）正确序号为（1）（3）（4）.

图13

反思对于（2）如图11，即在正方形半角模型中，用到两对全等三角形，△CBE≌△CKE，△CKG≌△CDG；（3）用到了模型中的第2个结论；（4）这个结论很有趣，是正方形半角模型的推论，实质是说明△CNH为等腰直角三角形，与例1中的△AMF为等腰直角三角形是一回事，如下图所示.当∠NCG＝45°，设BD交CG于H，则△CNH为等腰直角三角形（图14），同样△CGL也是等腰直角三角形（图15）.把半角45°角顶点放在A处（图16），就是例1中第（3）结论.2021黄石和葫芦岛两地的这道试题有异曲同工之妙.

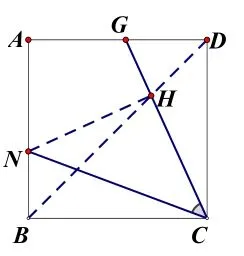
图14

图15

图16

例3（2021海南）如图17，在正方形ABCD中，点E是边BC上一点，且点E不与点B、C重合，点F是BA的延长线上一点，且AF＝CE.

图17

（1）求证：△DCE≌△DAF；

（2）如图18，连接EF，交AD于点K，过点D作DH⊥EF，垂足为H，延长DH交BF于点G，连接HB，HC.①求证：HD＝HB；②若DK·HC＝，求HE的长.

图18

解析（1）省略，证明正方形半角模型的基本做法就是旋转△DCE到△DFA.（2）中①根据条件暗合了∠EDG＝45°，即符合半角模型，△DEH为等腰直角三角形，只要说明C、H、A三点共线，与例2中第4个结论一致，作HM⊥AB，HK⊥AD（图19），易 知AH平 分∠BAD，同理CH平分∠BCD，即A、H、C三点共线，由对称性知HD＝HB.对于 ②结合HC＝，利用相似，即△DHN∽DKH，DH2＝，得DH2＝1，DH＝1（取正），即HE＝1.（图20）

图19

图20

反思通过旋转DE到DF，作DH⊥EF构图半角模型，其中EF中点H必在在AC上，本题中的H点即例1中的M点，例1和例3中部分条件和结论互换（即已知点M在对角线上，则M为某个等腰直角三角形斜边中点；已知H为等腰直角三角形斜边中点，则可说明H在对角线上），最终模型仍然是半角模.例2和例3则是构图半角模型的两种不同说法，例2以翻折变换陈述，例3以旋转变换陈述，万变不离其宗.

4 正方形半角模型结论的推广

上述几个2021中考试题都青睐正方形半角模型.事实上当45°角的一边与正方形边的延长线相交，同样具有类似的结论.

推广1如图21，在正方形ABCD中，点E、F分别在CB、DC延长线上，∠EAF＝45°，连EF，则（1）EF＝DF-BE；（2）∠AEB+∠AEF＝180°，∠AFD＝∠AFE.

图21

证明把△ABE绕A逆时针旋转90°到△ADG处（图22），则AG＝AE，再证△AFE≌△AFG，FG＝FE，∠AEF＝∠AGF，即得上述两结论.

图22

推广2如图23，在四边形ABCD中 ，AB＝AD，∠BAD+ ∠BCD＝180°，点E，F在BC和CD上，若，则（1）EF＝BE+DF；（2） ∠AEB＝∠AEF，∠AFD＝∠AFE.

图23

证明同推广1类似.（图24）

图24

5 对今后教学的建议和思考

数学解题模型就是解题中经常碰到的基本图形，基本结论.这些图形经典美妙，结论简洁明了，被广泛应用，具有强大的生命力.熟记这些结论，不仅可以提高解题速度、提高解题效率，而且有利于提高学生的数学构图能力、数学联想能力.

5.1 重视积累基本解题模型，提高识图能力

解题模型虽不是数学定理，但其作用不亚于定理.它是教学中总结出来的解题利器，经得起实践检验.它往往蕴涵着数学基本知识和基本处理方法.在复杂图形中若能发现或构造解题模型，就可以直接获取图形所蕴含的结论和方法，实现思维跳跃，节省解题时间.解题模型有助于提高学生的识图能力，有助于发展学生的构图能力，培养学生的创造性思维.

5.2 重视变式训练（条件和结论互换），提高对解题模型的实战性

有效的解题模型往往可以互换条件和结论，得到的新命题，结论具有相似性或互补性.变换模型的部分条件，从不同角度向外扩散，形成有规律可循的系列模型，有利于找到解决类似问题的思路和方法，提高解题模型的实战性.